COMSOL simulation of solute diffusion and infiltration behavior of geosynthetics clay liner

COMSOL Multiphysics以有限元为基础，通过求解偏微分方程(单场)和方程组(多场)实现多场耦合的仿真模拟^[34]，其建模过程一般分为基本假设及几何模型建立、确定物理场控制方程并赋予物理场、网格划分及求解3部分。

依据已有研究^[10,35-36]，考虑GCL孔隙率和扩散系数的影响，同时考虑美国材料与试验协会GCL系列测试标准(ASTM D6766)^[37]中膨润土基本达到饱和状态等条件，本研究数值模型建立的基本假设为：GCL为均一饱和介质，离子扩散与流体渗透具有相同曲折度，流体渗流满足达西定律。

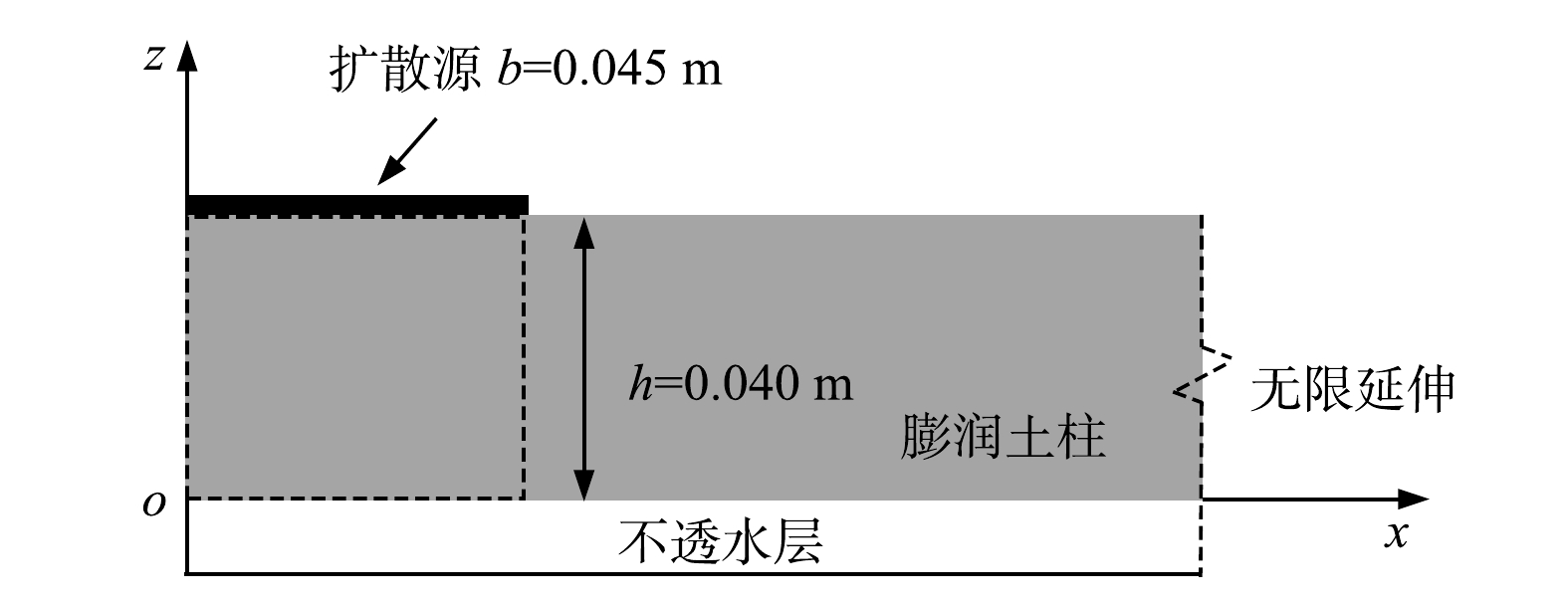
基于膨润土扩散柱实验^[38]，同时考虑边界无限延伸的工程实际，采用图1所示膨润土模拟扩散柱。其中，模型上边界和下边界设为沿x方向扩展的无限边界，上边界为膨润土柱上表面，下边界为不透水层边界。膨润土柱z方向上的高度h为0.040 m，扩散源宽度b为0.045 m(图1矩形虚线框所示)。初始扩散源均匀分布在图1箭头所示平面位置。

质量守恒时，单位体积多孔介质的浓度随时间的变化量可以用扩散项、对流项、吸附项、源项与衰变项等表示见式(1) ^[39]。

式中：θ_l为体积含水量，表示为非饱和土的含水率；C为溶质浓度，mol∙m⁻³；$\nabla ({\theta _l}{D_{eff}}\nabla C)$表示为单位体积多孔介质内受扩散系数影响随浓度变化的扩散项；$u\nabla C$为流速场和浓度梯度引起的对流场，u为达西流速，m∙s⁻¹；$\frac{\partial }{{\partial t}}({\rho _d}{C_s})$为受干密度影响的溶质吸附项；qC_R为源项，q为单位体积流入的源体体积流量，1∙s⁻¹；C_R是源体的浓度，mol∙m⁻³；ζ₁和ζ₂分别表示为物质在过程中发生反应降解和衰变的速率，mol∙m⁻²∙s⁻¹。

当GCL内膨润土基本达到饱和时，式(1)左侧的θ_l C随时间的变化率见式(2)。

求解过程中溶质质量守恒且无外部溶质流入，则有$q = \frac{{\partial {\theta _l}}}{{\partial t}}$。同时，考虑模型假设GCL为连续介质，微元体内有C_R=C。因此，qC_R如式(3)所示。

由于渗流过程温度恒定，同时多孔介质GCL为基本饱和状态，其孔隙率基本不发生变化，因此，溶质不发生衰变且有θ_l=n。将式(2)和式(3)代入式(1)，则得到控制溶质浓度扩散的非稳态扩散连续性方程如式(4)所示。

Cl⁻、Ca²⁺、Zn²⁺是常见的垃圾填埋场渗沥液所包含的离子，参考扩散柱实验结果^[38]，本研究选择CaCl₂、ZnSO₄为初始扩散源溶质，研究化学溶质在GCL中的扩散行为，具体参数汇总如表1所示。参考已有实验数据^[20,40-42]，选定模型中Cl⁻、Ca²⁺、Zn²⁺的扩散系数如表2所示。

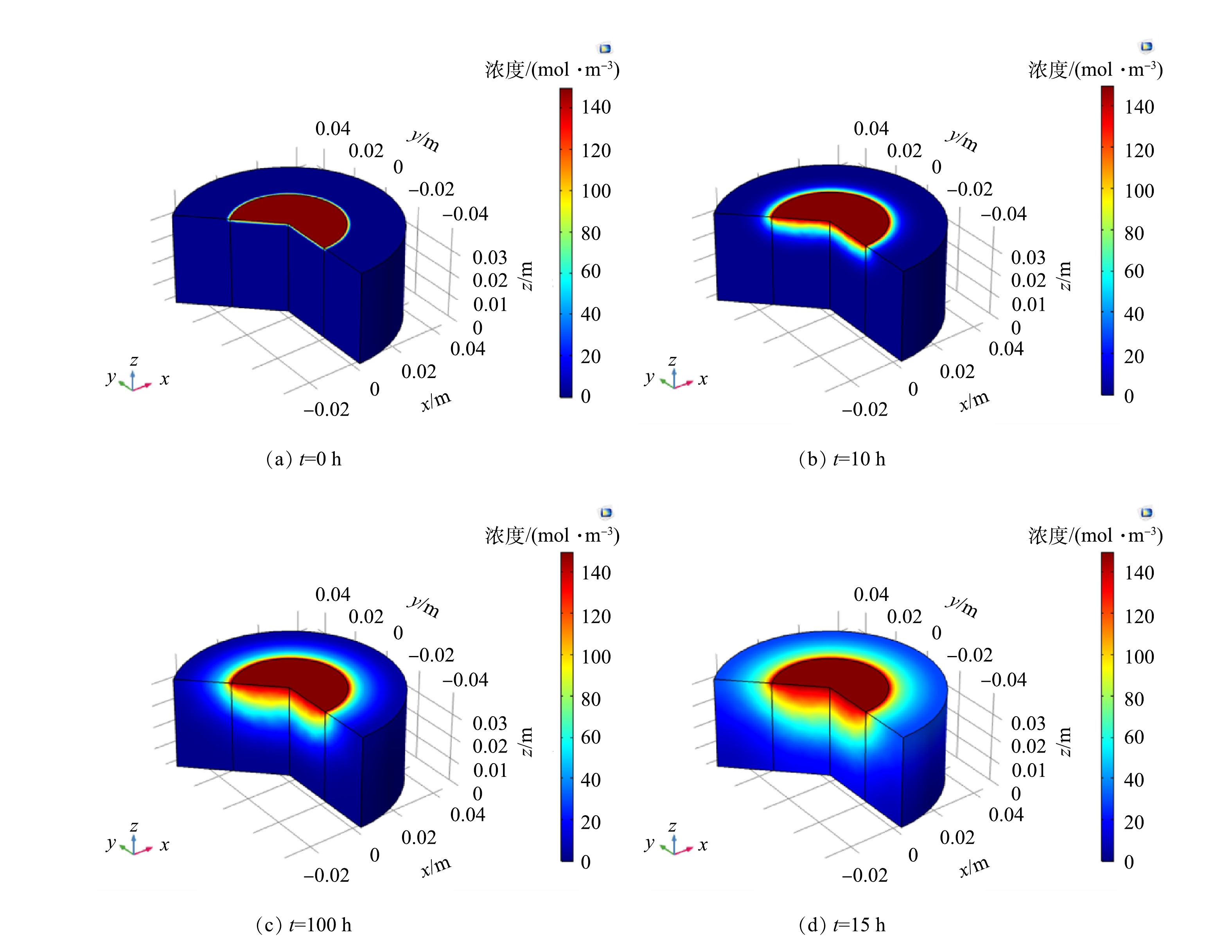
图2所示为Ca²⁺在不同时刻的扩散浓度分布图。比较图2(a)至2(d)可以看出，由于模型假设了GCL为均匀介质，因此Ca²⁺浓度分别在

3个方向是均匀扩散的。但是，Ca²⁺在竖直方向(z方向)的扩散速率明显大于水平方向的(x和y方向)。这是因为竖直方向为流体渗流方向，同时，溶质浓度随化学溶质的扩散会产生一定梯降，该梯降会加速GCL由均匀介质向非均匀介质转换，最终使得Ca²⁺在竖直方向的扩散速率最大。此外，比较图2(a)至2(d)可以看出，Ca²⁺浓度的扩散速度随时间的增长而逐渐减小。以Ca²⁺扩散浓度达到60 mol∙m⁻³时为例，10、100、150 h后，Ca²⁺运移的深度分别为0.005、0.015、0.02 m，对应的Ca²⁺平均运移速度分别为0.005、1.5×10⁻⁴、1.3×10⁻⁴ m∙h⁻¹。此外，从t=0 h至t=100 h时间内，Ca²⁺扩散浓度随深度变化较大。但是，在t=100 h至t=150 h之间，Ca²⁺扩散浓度随深度的增加而逐渐减小。当t=150 h，基本达到扩散平衡^[38]。因此，下节以t=150 h溶质扩散基本达到平衡时为例，进一步比较分析不同离子浓度和不同离子种类在GCL中的扩散规律。

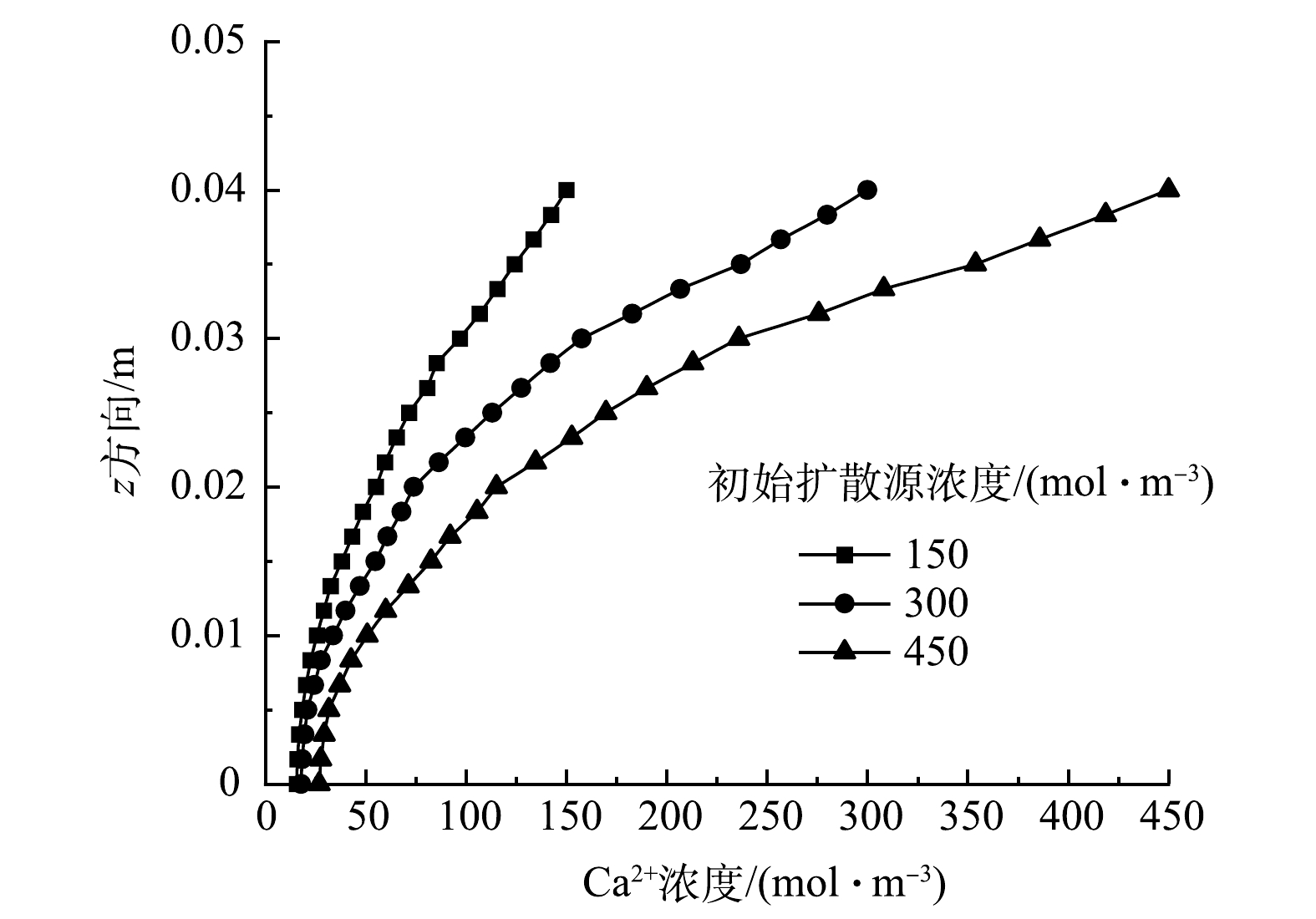
图3给出了t=150 h时，浓度分别为150、300、450 mol∙m⁻³的Ca²⁺初始扩散源在z方向的浓度分布图。可以看出，相同竖向位置处，Ca²⁺扩散浓度随初始扩散源浓度的增加而增大，即溶质的扩散作用随着初始扩散源浓度的增加而增大。进一步比较浓度为150与300 mol∙m⁻³的Ca²⁺初始扩散源随深度方向的扩散浓度梯降发现，溶质扩散的梯降随深度增加而逐渐减小。此外，比较初始扩散源浓度为150与300 mol∙m⁻³、300与450 mol∙m⁻³的曲线可以看出，初始扩散源处，溶质浓度差均为150 mol∙m⁻³。但是，溶质扩散后的浓度差与深度呈非线性变化关系。比如，当z=0.03 m时，初始扩散源浓度为150与300 mol∙m⁻³的浓度差值大于初始扩散源浓度为300和450 mol∙m⁻³的。但是，当z=0.01 m时，初始扩散源浓度为150与300 mol∙m⁻³的浓度差值小于初始扩散源浓度为300与450 mol∙m⁻³的。这说明，溶质在GCL中的扩散，不仅与初始扩散源的浓度有关，而且与扩散距离有关。扩散平衡时，初始扩散源附近，低浓度和中浓度的溶质影响范围较大。但远离初始扩散源处，高浓度初始扩散源的溶质扩散衰减较慢，因此影响范围更大。即低、中和高浓度初始扩散源的影响作用具有相反趋势。因此，当填埋场初始溶质浓度较高时，应尤其对较深范围可能出现的污染进行监测。

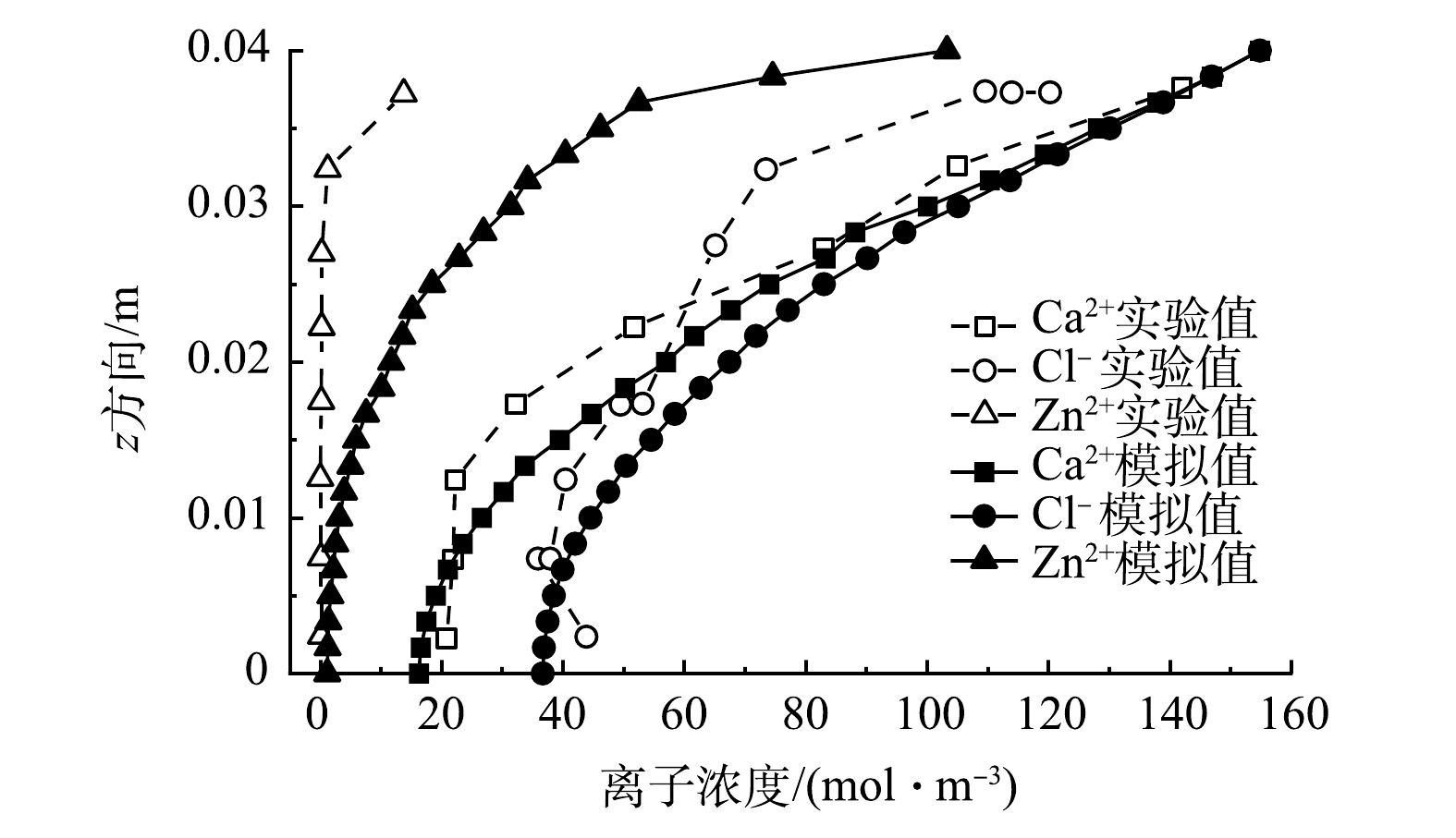
图4给出了t=150 h时扩散场作用下z方向不同种类离子扩散浓度随深度变化的模拟和实验曲线^[38]。可以看出，Ca²⁺、Cl⁻、Zn²⁺的模拟值与实验值均表现为离初始扩散源越远(z值越小)离子浓度越小的规律。同时，比较Ca²⁺与Zn²⁺阳离子的模拟值发现，扩散系数越大(Ca²⁺>Zn²⁺)，离子随深度方向的浓度变化也越大，且随着扩散深度的增加，化学浓度变化逐渐减小。此外，整体Ca²⁺浓度的变化大于Cl⁻的，但是，Cl⁻浓度的差值随扩散深度的增加逐渐增大。这说明，阴离子扩散衰减的速率小于阳离子的。此外可以看出， Zn²⁺的模拟值较实验值偏大，但Ca²⁺的模拟值与实验值却非常接近。原因是Zn²⁺扩散系数远小于Ca²⁺的，但本研究在COMSOL模拟过程中仅考虑了GCL孔隙率和扩散系数的影响，未考虑膨润土吸湿膨胀及细观孔隙结构的影响。由此可以推测，对于扩散系数较大的阳离子，孔隙率和扩散系数就可以较好地表征其扩散行为。但是，对于扩散系数较小的阳离子，应进一步结合吸湿膨胀及细观孔隙结构演化研究其扩散行为。因此，实际填埋场工程中，应针对不同渗沥液特征，对相应的GCL采取不同安全评估标准。当渗沥液中含大量Ca²⁺等扩散系数较大的阳离子时，可采取常规测试GCL渗透系数的办法评估GCL的防渗性能。但当渗沥液中含大量Zn²⁺等扩散系数较小的阳离子时，应进一步加强分析离子在GCL中的运移和扩散特征，才能更准确地评估GCL的防污性能。

扩散实验较难在水头和上覆应力耦合效应下开展，因此，本研究以Ca²⁺为例，分别调整模型水头压力为3 和100 kPa，同时施加0、3、25、50、100、200和400 kPa等上覆应力，以研究水头和上覆应力耦合条件下GCL中溶质的扩散规律。

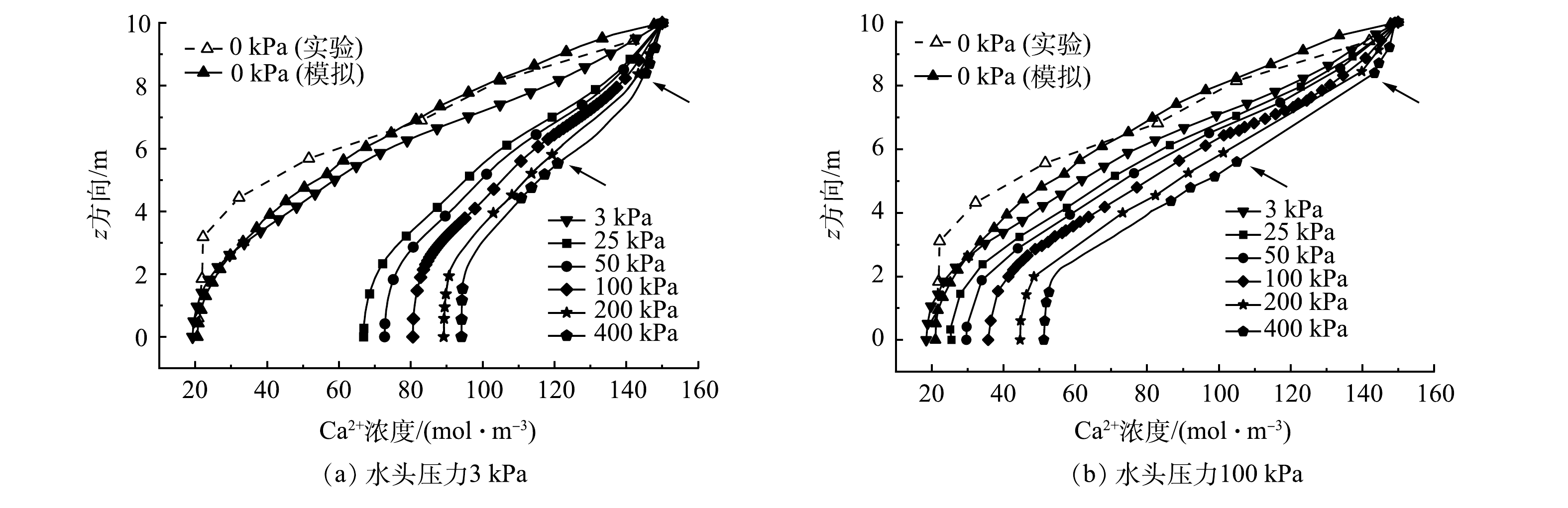
图5(a)所示为水头压力为3 kPa、上覆应力分别为0-400 kPa时，Ca²⁺浓度在z方向的变化曲线。可以看出，仅在3 kPa水头作用下，Ca²⁺浓度的模拟值与实验值基本一致。所有上覆应力下Ca²⁺浓度均随深度增加而呈逐渐减小的趋势，且随着上覆应力的增大，Ca²⁺扩散浓度随深度的变化逐渐减小。但是，上覆应力大于200 kPa时，Ca²⁺扩散浓度会在z=8.5和5.5 m位置处出现骤降点，即Ca²⁺扩散至该深度后，其扩散浓度随深度的增加而急剧减小。此外，值得注意的是，当上覆应力从3 kPa增加至25 kPa时，Ca²⁺扩散浓度的分布出现较大差异。以远离扩散源z=0 m处为例，当上覆应力分别为3和25 kPa时，该深度处Ca²⁺扩散浓度分别20和70 mol∙m⁻³，相差约50 mol∙m⁻³。而当上覆应力从25 kPa增加至400 kPa时，该处Ca²⁺扩散浓度仅相差约20 mol∙m⁻³。这说明，一定水头作用下，一定范围内的上覆应力会在初期较明显地增大GCL中化学溶质的扩散效应，进而促使化学溶质迅速扩散至较深的位置。因此，工程中应尽量避免干燥GCL直接上覆少量垃圾的情况，以防止垃圾填埋初期GCL的防渗性能明显降低。

图5(b)所示为水头压力100 kPa、上覆应力分别为0~400 kPa时，Ca²⁺浓度在z方向的变化曲线。可以看出，z=0 m时，上覆应力越大，同一深度处的Ca²⁺扩散浓度越大。上覆应力小于200 kPa时，Ca²⁺扩散浓度随深度变化比较均匀。而上覆应力大于200 kPa后，与水头压力为3kPa时类似，Ca²⁺扩散浓度会在z=8.5 m和5.5 m位置处出现骤降点，即Ca²⁺扩散至该深度后，Ca²⁺扩散浓度随深度的增加而急剧减小。其原因是，较大的上覆应力使得初始扩散源附近GCL的有效孔隙率明显减小，进而使得其内化学扩散效应显著受限。但随着深度的增加，上覆应力的压密效应逐渐减小，使得化学浓度较大时溶质的扩散效应随渗流明显增大。当z=5.5 m时，尽管上覆应力对有效孔隙率的减小受限，但是由于化学溶质浓度较小，因此GCL中溶质的扩散效应不再明显。继续增加深度后，上覆应力对有效孔隙率的减小几乎可以忽略，有效孔隙率逐渐增大，渗流的作用下，化学扩散再次趋于明显。由此也验证了GCL实验中，溶质的运移在化学和应力作用下存在耦合效应这一现象^[35]。

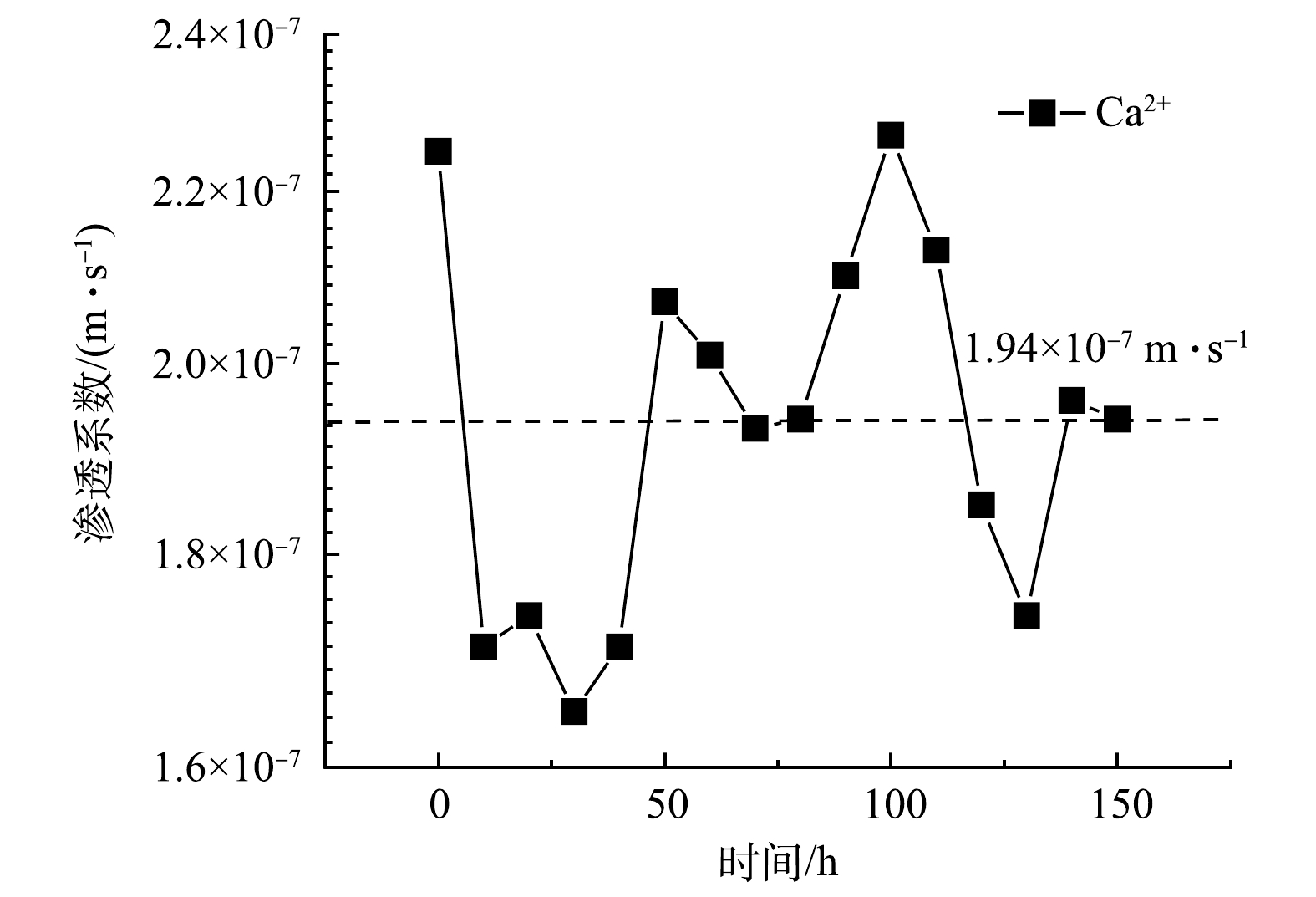
部分学者对膨润土的扩散系数和渗透系数及其相互关系进行了研究^[40-42]。图6给出了本模拟Ca²⁺扩散过程中GCL底部边界渗透系数随时间的变化规律。可以看出，随着Ca²⁺的扩散，其底部边界处的渗透系数约在1.6×10⁻⁷至2.3×10⁻⁷ m∙s⁻¹之间，当t=150 h扩散基本平衡时，渗透系数约为1.94×10⁻⁷ m∙s⁻¹。

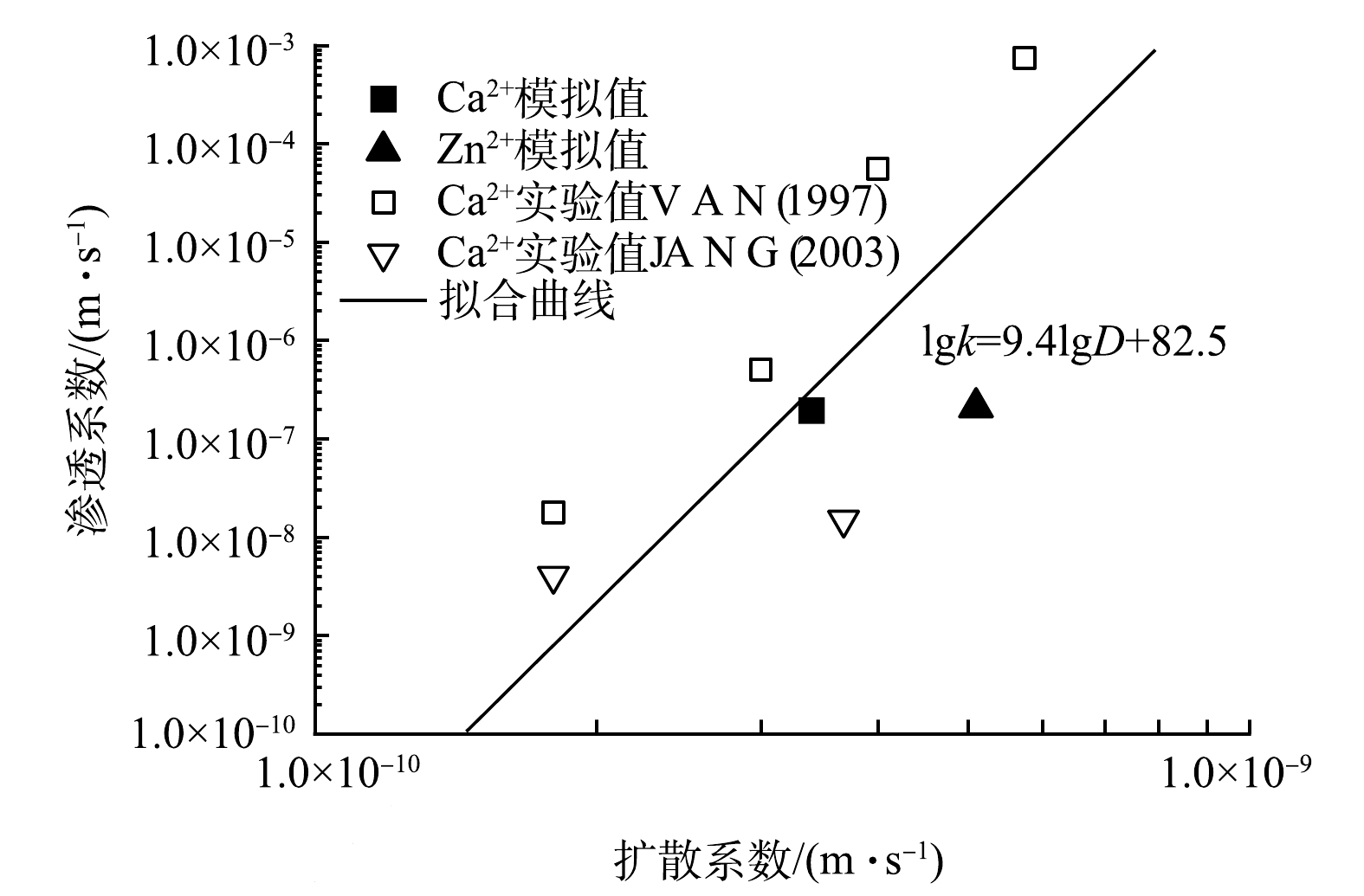
图7给出了本研究所得Ca²⁺和Zn²⁺扩散系数与渗透系数之间的模拟关系，同时汇总了JANG等^[43]和VAN等^[44]的实验值。可以看出，Ca²⁺的扩散系数和渗透系数值与相同条件下的实验结果非常接近。这说明，本模拟可以较准确地反应溶质在GCL中的扩散行为。同时，由于扩散系数与渗透系数在双对数坐标系下存在一定的线性关系^[44-45]，因此，通过拟合模拟和实验数据，可以得到双对数坐标系下渗透系数与扩散系数之间的关系如式(5)所示。

1)溶质在GCL中的扩散，不仅与初始扩散源的浓度有关，而且与扩散系数有关。溶质的扩散会加速溶质梯度的变化，扩散速度随时间的增长而逐渐减小，低、中浓度和高浓度初始扩散源的影响作用具有相反的趋势。填埋场工程中当溶质浓度较高时，应尤其注意较深范围内可能出现的污染。

2)扩散系数越大，离子随初始扩散源主扩散方向的浓度变化越大，阴离子比阳离子扩散衰减的速率小。孔隙率和扩散系数可以较好地表征扩散系数较大阳离子的扩散行为，但吸湿膨胀及细观孔隙结构演化等对扩散系数较小阳离子的扩散行为影响不可忽略。

3)化学和应力对溶质在GCL中的扩散存在明显的耦合效应。一定水头作用下，上覆应力会加速GCL中化学溶质向较深位置扩散。填埋场工程中应尽量避免干燥GCL直接上覆少量垃圾的情况，以避免GCL的防渗性能在填埋初期明显降低。