Research on traceability method of unorganized VOCs emission in industrial park under low wind condition

对于小风与静风的区分，至今尚无统一规定的方法。有2种应用普遍的划分方法：一种是将风速为0.5 m·s⁻¹≤ u≤1.5 m·s⁻¹规定为小风，将风速u<0.5 m·s⁻¹时^[14]，规定为静风天气；第二种划分方法是将风速u小于1 m·s⁻¹时规定为静风天气，而当风速u≤0.5 m·s⁻¹时定义为准静风^[14]。本研究采用第一种方法。由于小风属于极端天气，在该天气状况下，VOCs的扩散呈现一定特殊性。

常用于处理污染物扩散规律的高斯烟羽模型适用于风速u大于1.0 m·s⁻¹的条件，最好是在流场均匀定常且风速大于1.5 m·s⁻¹的气象条件下。而在小风气象条件下，虽然其污染方向与有风模式都为下风向，并且二者地面浓度分布在图形上相似，但是在x方向即平均风向的湍流扩散速率远小于平均风速的平流输送速率的这一假设不能成立，这使得高斯扩散模型无法处理小风条件下的VOCs扩散情况^[14]。在小风条件下，污染物VOCs扩散需考虑不稳定风场使得烟流活动不规则的情形，而烟团积分模式可很好地分析不稳定风场对VOCs扩散的影响^[15]。因此，基于烟团扩散模式构建了小风条件下的工业园区VOCs扩散的浓度预测模型。烟团积分模式的数学描述如后文所示。

在无界无风条件下，假设某污染点源释放了一个VOCs烟团，在 x、y、z 3个方向上的扩散都呈正态分布，则该烟团中心会一直保持与释放点源重合。以烟团释放点为坐标原点建立坐标系，经过时间t后，该VOCs烟团对空间中某点(x，y，z)的VOCs贡献可依据式(1)计算。

式中：Q_i为VOCs烟团质量浓度，μg·s⁻¹；σ_x、σ_y、σ_z分别为x、y、z方向上的扩散参数，m；t为烟团运行时间，s。

而在无界有风条件下，VOCs烟团会沿风向移动。假定风向为x方向、风速为u，则烟团中心会沿x方向相对于VOCs烟团释放点移动ut距离。若以烟团中心为相对坐标系，则空间中某点坐标可表示为(x-ut，y，z)。此烟团对下风向监测点的VOCs质量浓度贡献可依据式(2)计算。

在有界有风条件下，做出如下假设：1)不考虑地面对VOCs吸附和吸收作用；2)不考虑VOCs的沉降作用；3)认为地面对VOCs的散布具有全反射的作用；4)不考虑VOCs烟团的抬升高度。因此，在有界有风条件下，VOCs烟团到下风向监测点的浓度贡献可依据式(3)计算。

式中：H为有效点源高度，m。

进一步地，将烟团积分扩散模式拓展到小风气象条件下连续点源的扩散中。假定点源排放源强为Q，则可把在△t时间段内排放的VOCs视为一个烟团，依据式(4)可计算经过时间△t后烟团在下风向监测点处的瞬时浓度。

连续点源到下风向监测点处的质量浓度，可看作是在一定时间段t内连续释放的VOCs烟团对此下风向监测点的质量浓度总贡献。因此，根据式(4)对t进行积分，得到连续点源在小风场景下的扩散模型，如式(5)所示。

当Z=0时，即可推导出污染物VOCs地面浓度表达式(6)。

在烟团扩散污染物浓度的计算中，需确定在x、y、z 3个方向上的扩散系数，即σ_x(t)、σ_y(t)和σ_z(t)。其中，t表示该烟团的存在时间或者该烟团从释放到当前的运行时间。当大气稳定度用P-S方法分为6类时，扩散参数表示为σ_x=σ_y=γ₁t，σ_z=γ₂t。t的单位为s。γ₁、γ₂在表1中选取^[15]。

由表1可得到小风气象条件下，x、y、z 3个方向上扩散系数计算方法的参数值。结合式(6)，能计算出在小风条件下污染物VOCs对下风向监测点的质量浓度贡献。

能较准确地模拟面源污染物分布的计算方法主要有2种。一种是由Hanna和Gifford提出的大气湍流与扩散实验室模式(Atmospheric Turbulence and Diffusion Laboratory)，即ATDL模式或者窄烟云模式。由于其形式简单计算方便，过去常被用于计算城市面源^[16]。该模式基于高斯正态烟羽模型推导出简化模式，并没有对小静风这一气象条件进行考虑，故不能做小风条件下的污染物浓度计算。另一种计算方法是虚拟点源后置法，目前被广泛用于各种面源计算中^[17]。该方法不仅适用于有风条件下的面源计算，而且也可用于小静风气象条件下的面源计算。在有风气象条件下对面源进行计算时，重点是为了求排放面源中心点位向上风向推移的虚点源距离^[15]。而在小风条件下对面源进行计算时，点源后置法重点是为了求瞬时烟团从面源中心点排放后增加的一个虚拟排放时间^[16]。

对小风条件下的无组织VOCs排放面源进行研究，假设条件为：1)面源内部VOCs是均匀排放的；2)面源可看作是由许多面积很小的面源单元组成；3)高斯面源扩散虚拟点源后置法即增加了一个初始的扩散系数(σ_y0和σ_z0)。

在小风条件下，面源计算采用烟团扩散模式。相比于针对高架点源的扩散模型，烟团积分面源扩散虚拟点源法相当于瞬时烟团从面源中心点排放后，增加了一个初始虚拟排放时间。如当第一个瞬时烟团释放后，以瞬时烟团中心浓度的1/10作为烟团的可见边缘，而烟团的边缘恰好与面源相等。采用反时间扩散参数，可求出增加的初始虚拟排放时间^[18]。

若扩散参数为σ=γt的形式，则虚拟排放时间可以式(7)～(8)表示。

因此，可,根据式(6)得到小风条件下面源的扩散模型（式（9）），参数见式（10）。

式中：σ_xm为顺风向的扩散参数(=σ_ym)，m；σ_ym为横风向的扩散参数，m；σ_zm为垂直方向的扩散参数。

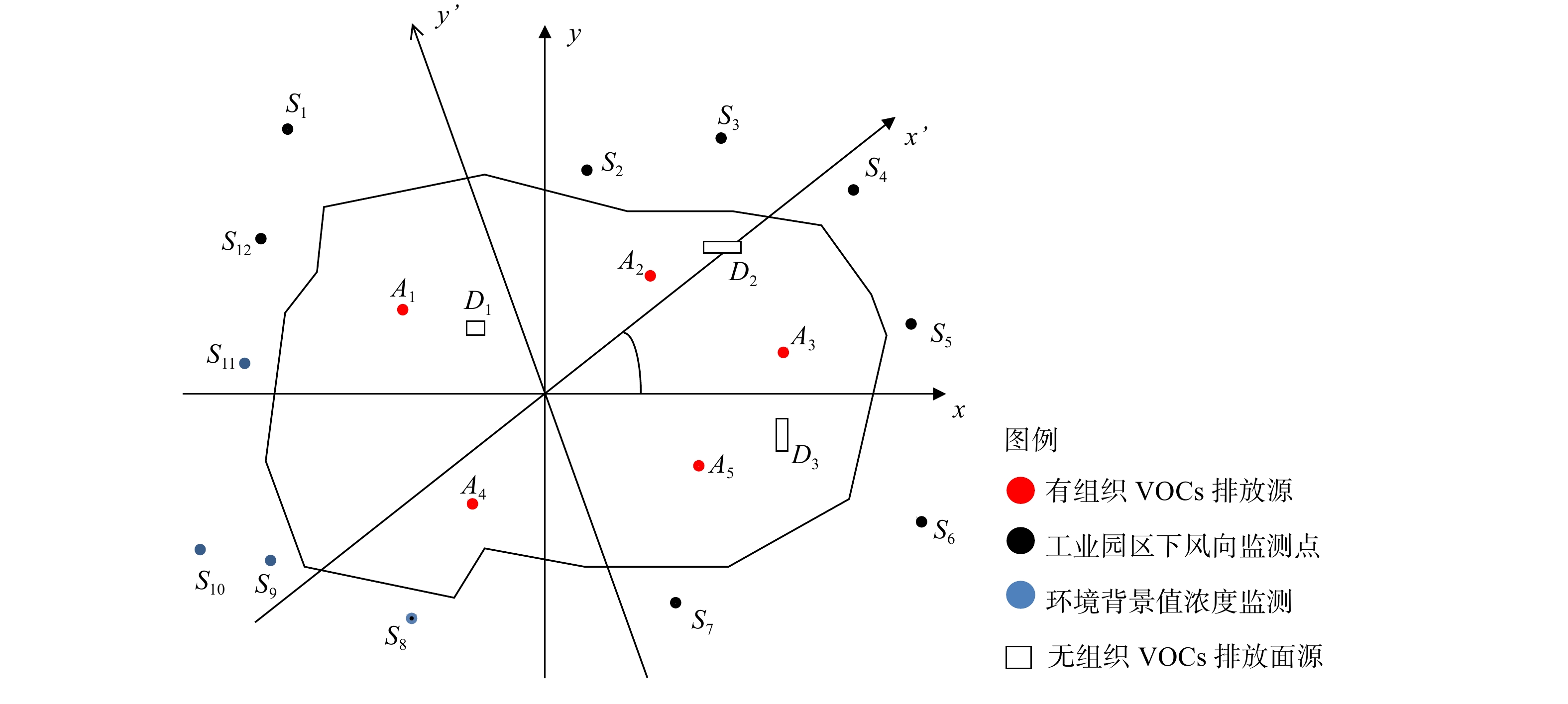
首先，对所选定的工业园区进行剖析。将该园区的中心位置设定为坐标原点O(0，0，0)。z轴为垂直于x、y轴所在平面，加上x、y轴来建立笛卡尔坐标系。原点O的正东方即x轴的正向轴、正北方即y轴正向轴。由此定义工业园区内的有组织排放源分别为A_r(r=1，2，…，R)，工业园区的周围监测点分别为S_m分别为(m=1，2，…，M)，无组织面源排放点分别为S_t(t=1，2，…，T)。图1表明了园区内各排放源在x、y轴所在平面的位置。其中，r为有组织排放源的编号，R为整个工业园区内有组织排放源的总个数；m为监测点的编号，M为整个工业园区周边监测点的总个数；t表示无组织面源的编号，T为整个工业园区内无组织面源的总个数^[19]。

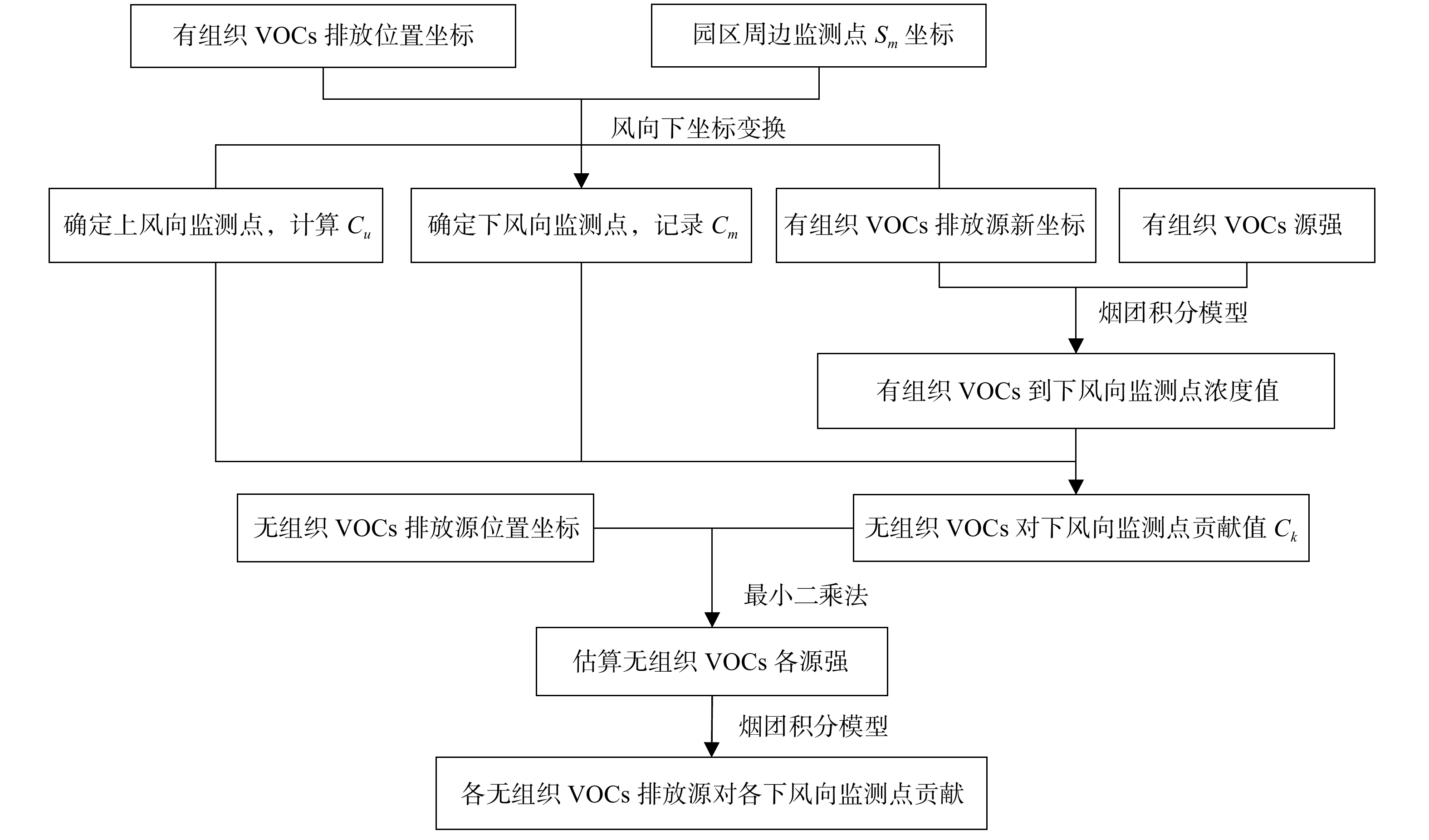
小风条件下工业园区VOCs排放场景如图1所示。为明确小风条件下，下风向监测点的无组织排放源在哪个点(D_t)。首先，应确定无组织面源D_t的排放源强，而无组织VOCs排放在空气中量化是非常困难的，因此考虑通过已知资料来反推无组织排放的VOCs源强。由于下风向监测点监测到的总挥发性有机物(total volatile organic compounds，TVOCs)主要由3部分组成：VOCs环境背景值，有组织排放源和无组织排放源分别对园区下风向监测点的贡献值。TVOCs和园区背景值，以及计算得到的有组织排放源对下风向监测点贡献值，则得到无组织排放源对监测点的贡献，然后基于无组织排放源对监测点贡献，反推无组织排放源强^[19]。本研究基于工业园区VOCs环境背景值C_u、园区下风向监测点TVOCs(C_m)、有组织VOCs排放源的源强及位置，以及扩散模式反推法来构建小风条件下无组织VOCs排放溯源模型(图2)。

随着风向的变化，园区的下风向监测点亦会改变。因此，为了能快速确定风向角θ，以便准确计算下风向监测点的VOCs质量，从而区分出上下风向的监测点。图1表明，该黑圆点S_v(1≤v≤M)属于园区下风向监测点，而蓝色圆点S_u(1≤u≤M)为园区的上风向监测点，用来计算园区的环境背景值浓度。本课题组提出了一种方法以快速确定工业园区上下风向监测点，即规定沿逆时针方向(以正东向为起点)转动的角度称为风向角，记为θ(0^。≤θ≤360^。)。此时x正向轴与风向相同，也就是将原坐标系整体绕z轴旋转了θ度。将按照上述方法，得到有组织排放源A_r新的位置坐标($x'_{{A_r}},y'_{{A_r}},z'_{{A_r}}$)表达式(式(11))。相应的监测点位S_m新位置坐标($x'_{{S_m}},y'_{{S_m}},z'_{{S_m}}$)的表达式为式(12)。

对于工业园区中的一个污染源A_i，当园区周边监测点的横坐标$x'_{{S_m}}$小于污染源A_i的横坐标$x'_{{A_i}}$时，对应的监测点为该污染源A_i的上风向监测点S_u；而当监测点的横坐标$x'_{{S_m}}$小于园区内所有污染源的横坐标时，则将其定为这一园区的上风向监测点位，也就是工业园区背景值浓度的监测点。

园区内有组织排放源A_r的位置坐标和排放源强${Q_{{A_r}}}$，可通过对各企业进行监测分析得到。将超过15 m、且集中有规则排放的污染源称为有组织排放源。故选用针对于高架点源的烟团积分模式扩散模型来对计算有组织排放源A_r扩散到下风向监测点S_v的浓度值C_l，其计算公式见式(13)。

在笛卡尔坐标体系下，当风向角为θ时，有组织VOCs排放源A_r和监测点S_m的位置坐标会转化为新的坐标，此时以工业园区的中心为坐标原点建立坐标系，计算小风条件下有组织VOCs排放源A_r到下风向监测点的浓度值C_l，计算式如式(14)所示。

式中：H为有组织排放源的有效源高，排放源到原点O点的垂直距离${z_{{A_r}}} 等于 H$，m；($x'_{{S_v}} - x'_{{A_r}} - ut$)为下风方向监测点S _v到有组织VOCs排放源的距离，m；($y'_{{S_v}} - y'_{{A_r}}$)为横向距离，m；$z'_{{S_v}}$为垂直地面的距离，m；${\sigma' _{x_{{S_v}}}}$为x轴方向的扩散系数，m；${\sigma _{y'_{{S_v}}}}$为y轴方向的扩散系数，m；${\sigma _{z'_{{S_v}}}}$为z轴方向的扩散系数，m。

实际上，小风气象条件不可能是无限时长，只需取当前时刻之前1 h时长即可获得较为准确的监测点污染物小时质量浓度均值，故式(10)中的积分上下限可换成有限区间。为提高计算速度，采用Matlab基于烟团的积分模式即可对有组织VOCs排放源到下风向监测点的浓度值进行计算。此处的数值积分可采用Simpson(辛普森法)。

在风向角为θ的情况下，根据式(12)转换监测点位S_m的坐标(${x_{{S_m}}},{y_{{S_m}}},{z_{{S_m}}}$)，以获得新的位置坐标($x'_{{S_m}},y'_{{S_m}},z'_{{S_m}}$)。$x'_{{S_m}}$的定义为园区内所有污染源的横坐标的最小值，故其为背景值浓度的监测点。为了减小误差，对各背景值监测点的数据进行求和，计算平均值得到环境背景浓度值，记为C_u(见式(15))。

式中：W为背景值浓度监测点的有效个数。C_m表示下风向监测点的TVOCs，根据式(14)得到有组织排放源A_r扩散到下风向监测点位的C_l，从而推出小风条件下无组织排放源扩散到下风向监测点浓度值，即C_k，计算式见式(16)。

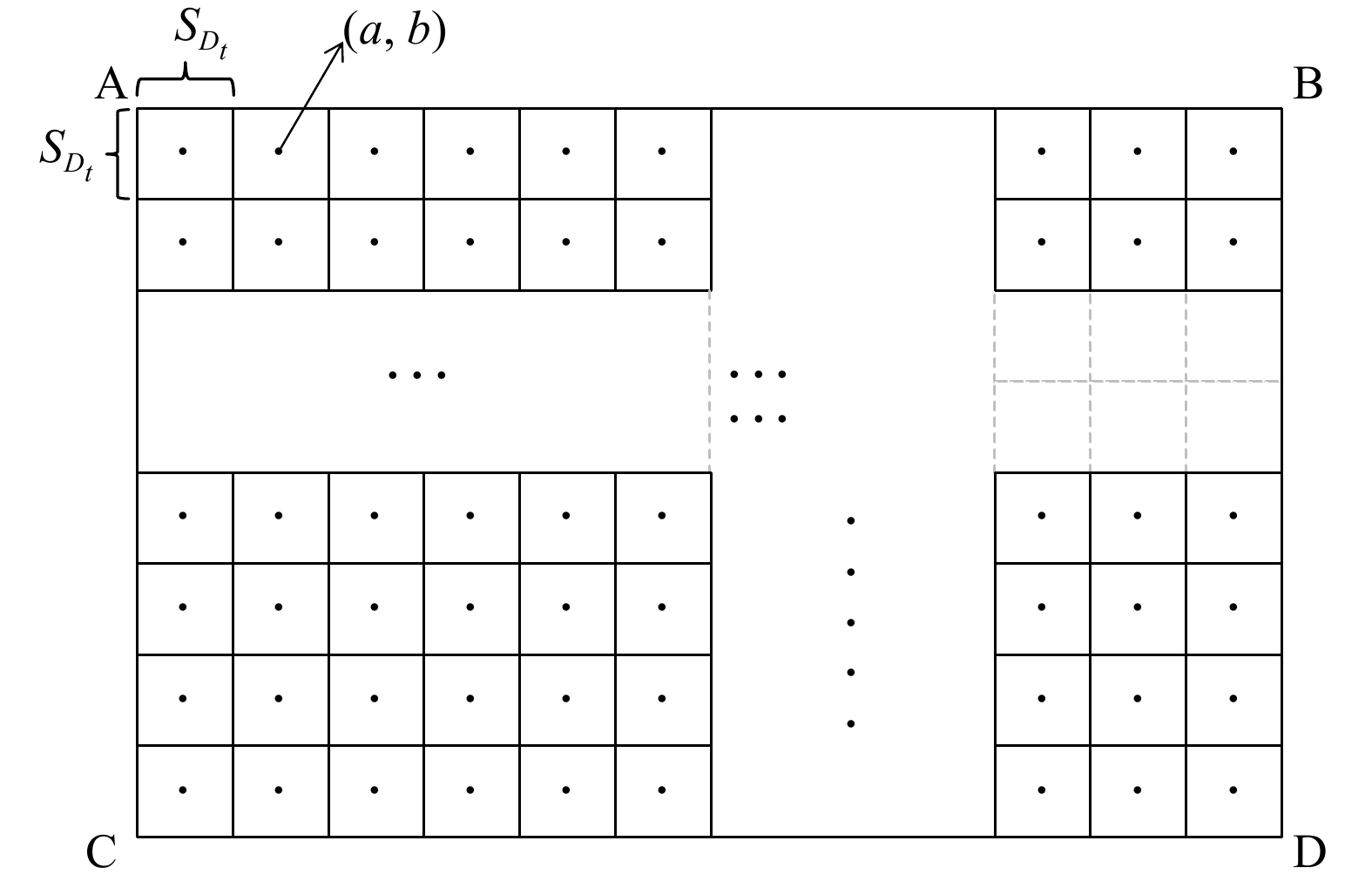
由于虚拟点源后置法是以正方形的单位面源为研究对象，并且必须确定其中心位置。在园区内，一般将无组织排放面源形状确定为长方形。为提高计算精度，将单位面源的边长L定义为无组织排放面源长方形的长宽最大公约数${s_{{D_t}}}$，并以L等分无组织排放面源，每个单位面源即为单位研究对象。为方便计算，首先需计算出各单位面源的中心位置坐标，计算步骤如下。

1)在原始坐标系下确定出各无组织VOCs排放面源(D_t)顶点的位置坐标，并将其按逆时针顺序排列为A(${x_{{D_{At}}}},{y_{{D_{At}}}},0$)、B(${x_{{D_{Bt}}}},{y_{{D_{Bt}}}},0$)、D(${x_{{D_{Dt}}}},{y_{{D_{Dt}}}},0$)、C(${x_{{D_{Ct}}}},{y_{{D_{Ct}}}},0$)。

2)利用面源的顶点坐标得到各面源D_t的长${a_{{D_t}}}$和宽${b_{{D_t}}}$，计算${a_{{D_t}}}$、${b_{{D_t}}}$的最大公约数${s_{{D_t}}}$，再将D_t分成m个相等面源，以得到各单位面源的中心位置坐标(${x_{D_t^{ab}}},{y_{D_t^{ab}}},0$)(图3)。中心坐标计算公式见式(17)～(18)。

式中：i表示宽${b_{{D_t}}}$可被分成相等的${s_{{D_t}}}$分成相等的i份；j表示长${a_{{D_t}}}$可被分成相等的j份，长度亦为${s_{{D_t}}}$；单位面源所在行为a；单位面源所在列为b；无组织面源D_t中的第(a，b)个单位面源定义为ab；等分成面积相等的正方形个数即m。步长d = L/2。

3)当风向角为θ时，(${x_{D_t^{ab}}},{y_{D_t^{ab}}},0$)会按式(11)变换成($x'_{_{D_t^{ab}}},y'_{_{D_t^{ab}}},0$)。

因每个无组织VOCs排放面源按各自边界长宽的最大公约数，会被等分成m个单位面源，因此，计算得到的在第t个无组织面源中，第(a，b)个单位面源到下风向监测点的浓度值为${C_{D_t^{ab}}}$，计算式见式(19)。

通过式(19)计算面源单元到工业园区下风向监测点的VOCs质量浓度。计算无组织面源D_t到工业园区下风向监测点的浓度值时，只需对该无组织面源D_t的m个面源单元到监测点的浓度值进行叠加即可(见式(20))。

由于无组织VOCs面源的排放源强很难直接准确监测，故在无组织VOCs溯源过程中，通过反向计算，得到无组织面源排放源强。式(16)可计算无组织VOCs排放源对监测点的浓度贡献C_k，而无组织面源D_t的位置坐标可通过调研工业园区相关资料得到，然后通过反算模型求解排放面源的源强。

假定园区内总污染源有T个，并在园区周边设定V个监测点。K则反映了某污染源与某监测点的浓度值响应关系。监测点数据为各无组织排放源贡献总和，故上述过程可用式(21)来描述，另可将式(21)展开为矩阵形式(式(22))。

式中：Q为源强，μg·s⁻¹；$C_k^v$为监测点的测定值，μg·m⁻³。Q_t为第t个无组织污染面源的排放源强，μg·s⁻¹；$C_k^v$为无组织排放源对第v号监测点质量浓度的贡献，μg·m⁻³；K_vt为第v号监测点浓度与第t个污染源排放源强的响应关系(计算式见式(19))。

以无组织面源D_t的长${a_{{D_t}}}$与宽${b_{{D_t}}}$最大公约数为边长，将无组织排放面源等分成m个源强为${Q_{D_t^{ab}}}$的单位面源。其中，${Q_{D_t^{ab}}} = {{{Q_{{D_t}}}} \mathord{\left/ {\vphantom {{{Q_{{D_t}}}} m}} \right. } m}$，每个小正方形(a，b)对监测点的浓度贡献值可通过式(19)得到，并通过式(23)计算K_vt。

故式(23)可推导为式(24)。

在T=V的情况下，可直接列式然后对方程组进行求解。但实际情况下，总的监测点数目要比污染源的数目多，也就是T<V，可列式构成一组超定方程组。因此，采用最小二乘法对超定方程组求解。由于难以量化空气中的无组织排放源强，故以园区下风向监测点监测到的TVOCs、环境背景值和计算得到的有组织排放源对下风向监测点的贡献值来推算无组织排放源对各监测点贡献值，并以此作为无组织排放的实际源强，再反演出无组织排放源源强，从而得到无组织排放源到下风向监测点的理论计算值。用式(25)分析理论值与实际值间的偏差。为了便于计算，采用Matlab编制程序对超定方程组进行求解。式(25)中$C_z^i$表示所有无组织VOCs到监测点i的计算浓度值之和。

利用上述方法，可以得到各无组织VOCs的排放源强，然后通过烟团积分模型，计算出各污染源对各监测点的浓度贡献。假定工业园区中有T个无组织VOCs的排放源，需在小风条件下对各无组织VOCs排放源到每个监测点的浓度贡献比例进行计算和分析，用p_i进行表示，其中1≤i≤V。

根据前文提出的计算无组织排放源强的方法，可计算T个无组织排放源强(${Q_{{D_1}}}$，${Q_{{D_2}}}$，…，${Q_{{D_T}}}$)。以第i个无组织排放源为例，如果仅考虑第i个排放源对第j个监测点的贡献，则第j个监测点的污染物质量浓度仅受第i个排放源影响。假定在某场景中，第i个无组织排放源强Q_i未改变，而其他无组织排放源强设为0，即${Q_{{D_1}}}$=${Q_{{D_2}}}$=…=${Q_{{D_{i - 1}}}}$=${Q_{{D_{i + 1}}}}$…=${Q_{{D_T}}}$=0，再根据小风条件烟团积分模型，即得到第i个无组织排放源对第j个监测点的贡献C_ij(计算式为式(26))。

式中：f为烟团积分模型；P_mete为气象相关参数。

基于以上思路构建T-1个相似情景，分别仅考虑某个无组织排放源对监测点j的影响，而其他未被考虑排放源源强为0^[20]，即得到其他排放源对监测点j的贡献值(计算式为式(27))。

各无组织VOCs排放源对监测点j的污染物浓度的贡献比例计算如式(28)所示。

图4为西安市某工业园区所在区位的ArcGIS图，展示了工业园区所在地形地势。案例分析所用数据中，有组织排放源强数据来自企业年报，园区周边监测点坐标来源于国家环境空气质量监测网和地方统计年鉴；监测点TVOCs来源于国家环境空气质量监测网和天气后报网站；气象数据来自于美国国家气候数据中心；污染源位置坐标来自企业披露公开信息。

所选工业园区内各VOCs排放源所在位置坐标参数介绍如下。建立笛卡尔坐标系，坐标原点即工业园区中心，x正轴为地理正东方向，y轴正向为地理正北方。将各排放源及监测点的位置在坐标系中进行标记，如图1所示。园区内部共有5个有组织排放点源(表2)，共有12个厂界监测点(表3)。另外，还有3个无组织排放面源。面源D₁的长为67 m，宽为67 m；面源D₂的长为219 m，宽为54 m；面源D₃的长为60 m，宽为40 m；排放面源D_t顶点坐标的见表4。

分析园区2020年9月5日10:30—11:30的监测数据。此时为小风条件：大气稳定度为B，平均风速为0.9 m·s⁻¹，扩散参数的系数γ₁=0.56、γ₂=0.47。这一时段内主导风向为NE，即就是正东方逆时针旋转45^。，如图1所示。通过式(11)～(12)可以得到有组织VOCs排放点源A_r及园区周边监测点位置S_m的新坐标(见表5和表6)。

排放点源A_r的逐小时排放源强${Q_{{A_1}}}$依次为2.4 g·s⁻¹、2.0 g·s⁻¹、3.0 g·s⁻¹、3.5 g·s⁻¹和2.5 g·s⁻¹。通过式(14)可计算出排放源A_r扩散到下风向监测点S_v(v=1，2，3，4，5，6，7，12)的质量浓度值C_l，结果见表7。

经过分析比较，可得到园区背景浓度监测点为S₈、S₉、S₁₀、S₁₁，对应质量浓度分别为0.06 μg·m⁻³、0.04 μg·m⁻³、0.14 μg·m⁻³和0.08 μg·m⁻³。另外，还要舍去明显高于其他监测点的数据，如10号监测点数据。根据公式(15)，可求得背景质量浓度C_u为0.06 μg·m⁻³。此时，园区的下风向监测点对应的VOCs监测值如表8所示，其中，C_k根据式(16)求得。

此时，工业园区的下风向监测点为S₁、S₂、S₃、S₄、S₅、S₆、S₇、S₁₂，其对应VOCs监测值如表8所示。其中，C_l根据3.2.1计算，C_k根据式(12)求得。

表4为面源D₁、D₂、D₃的顶点坐标。将D₁、D₂、D₃按照各自面源长宽的最大公约数进行等分。由式(17)、(18)求出xoy坐标系下各单位面源中心坐标，进一步通过坐标变换公式求出x’oy’坐标系下单位面源的新坐标，结果如表9所示。

该园区内有D₁、D₂、D₃三个无组织VOCs污染源。D₁视为单位面源，其源强为${Q_{{D_1}}}$；D₂可划分为4个单位面源，每个源强为${{{Q_{{D_2}}}} \mathord{\left/ {\vphantom {{{Q_{{D_2}}}} 4}} \right. } 4}$；D₃划分为6单位面源，每个源强为${{{Q_{{D_3}}}} \mathord{\left/ {\vphantom {{{Q_{{D_3}}}} 6}} \right. } 6}$。首先计算出第v号下风向监测点污染物质量浓度与各单位面源源强的比例系数(1≤a≤i；1≤b≤j)，然后求和得到第v号监测点浓度与面源D₁、D₂、D₃的比例系数K_vt(表10)，最后根据式(24)建立方程组式(29)。

式(29)采用最小二乘法求解，得出了无组织排放面源D₁、D₂、D₃的源强分别为4 855 700、2 810 960和3 484 740 μg·s⁻¹，并计算得到误差平方和R为0.001 5。

面源D₁、D₂、D₃的排放源强估算值、监测点测得污染物质量浓度及面源源强系数K_vt可由式(24)计算。第i个无组织排放源对第j个工业园区下风向监测点的贡献值C_ij(表11)根据式(26)计算。各无组织排放源对下风向监测点j的污染物贡献比例根据式(28)计算(表12)。

表12中数据表明，在小风条件下污染物扩散有明确的方向性，其地面浓度分布与有风模式地面浓度分布相似，但也兼具各方向扩散现象^[17]。在D₁的上风向监测点S₇、S₁₂，也监测到来自D₁的污染物。在D₁下风向监测点S₂、S₃距离很近，监测到的污染物浓度较高，与上述结论相符。D₂的上风向监测点为S₁、S₂、S₆、S₇、S₁₂，监测到了很少量来自于D₂的污染物，而S₃、S₄、S₅监测到的污染物浓度明显较高，亦验证了以上结论。同样，在D₃的上风向监测点S₁、S₇、S₈也监测到了很少量来自于D₃的污染物，且距离D₃最近的下风向监测点S₅污染物浓度最高。

1)选取工业园区作为研究对象，根据园区内部各VOCs排放源特点以及园区周边监测点监测值，通过小风条件下烟团积分扩散模式反推法构建工业园区无组织VOCs溯源模型，反算无组织VOCs排放源排放源强，进而求出下风向各监测点无组织VOCs排放源的浓度贡献。该方法即小风条件下，无组织VOCs排放溯源解析法。

2)距离污染源较近的下风向监测点监测到的VOCs浓度较高，而上风向监测点也监测到少量VOCs。在小风条件下，污染物扩散具有明确方向性同时兼具各方向扩散的现象。