-
随着我国工业化和城镇化进程的加速发展,工业结构调整和空间格局重构导致大批污染企业搬迁、改造或关闭,在城市及其周边地区遗留千万公顷污染场地,严重威胁居民健康和环境安全[1-4]。由于氯代烃、石油烃等有机污染物的溶解度较低,通常以非水相液体 (NAPLs) 存在于地下土水环境中并迁移形成污染羽。当存在有低渗透地层时,会在低渗透地层上形成污染池,并通过扩散作用或者天然裂隙侵入低渗透地层,形成持久性污染源[5]。现有抽提、氧化等原位修复技术[6-8]可以有效修复低渗透介质层上的污染池,但受限于物质传输速率,低渗透介质内的污染物难以被去除,导致修复反弹[5, 9-10]。因此,低渗透污染地层的修复是当前污染场地修复的重大挑战。
为了提升低渗透污染地层的渗透性,可以引入石油开采行业的压裂技术形成缝网结构,提升物质传输速率[11-13],与多相抽提技术形成协同工作模式,实现高效去除[14-16]。目前,国内外学者已针对压裂协同抽提修复技术开展了一系列研究。MURDOCH等[17]以未压裂抽提井为空白对照,设置2个压裂抽提井,发现压裂前后抽提流量提高了13~31倍,随着流动相和非流动相之间物质传质速率的增大,污染物去除率提高675%[18],论证了水力压裂与抽提协同的有效性。为了进一步揭示压裂对气相抽提的影响机制,SCHULENBERG和REEVES[19]建立了压裂协同气相抽提轴对称模型,发现裂隙长度对污染物去除率的敏感性不如裂隙渗透率;CHEN等[20]利用TMVOC代码和MINC方法,建立了双孔隙介质压裂协同热强化抽提数值模型,同样发现基质渗透率的敏感性远大于抽提压力、裂隙间距和孔径;BRANDNER和MURDOCH[21]利用数值模型,参考石油行业开采井的标量评价指标流动速率,定义裂隙有效流通率,量化评价裂隙对污染物去除率的影响。在试验方面,TZOVOLOU等[22]以砂层等效水力压裂裂缝,利用模型试验论证了裂缝中对蒸汽修复效率的强化作用,去除率可达77%,同时他们也在现场试验中论证了压裂协同生物通风修复低渗透污染土的技术有效性和经济性[23]。针对埋深9~12 m的污染低渗冰川土,CUSHMAN等[24]通过试验发现压裂后的多相抽提效率是压裂前的6倍;NILSSON等[25]则通过低渗污染场地的压裂协同抽提中试试验,发现气/水/非水相污染物均被负压抽提,而总NAPL的质量去除率达到30%。虽然,目前污染场地的压裂协同抽提修复的技术有效性均得到了试验和数值仿真的论证,但是现有研究仍主要以尝试为主,并将污染物去除率作为主要评价指标,缺乏对压裂增渗强化污染物去除机理的深入研究,特别是孔隙-裂隙介质中的优势渗流规律。
为此,本研究首先建立孔隙-裂隙介质中多相抽提数值模型,利用COMSOL MULTIPHYSICS软件进行求解,以低渗透污染地层污染程度、压裂缝网特征参数 (裂隙长度、厚度和渗透率) 开展单因素和多因素参数化分析,探究压裂缝网对低渗透NAPL污染地层多相抽提效率的影响机制。
-
饱和态孔隙-裂隙介质的多相抽提主要涉及2个过程,一是抽提作用下自由相和水相迁移,二是溶解相对流-弥散作用,由于自由相的浓度远高于溶解相,本研究主要考虑自由相污染物去除,因此忽略污染物的相间传质,并假设地层中初始污染物均匀分布。模型控制方程由孔隙介质与裂隙介质中的水相和NAPL相质量守恒方程、水力本构方程、溶解相污染物运移方程组成。
孔隙-裂隙介质中基质部分的水相 (w) 和NAPL相 (nw) 质量守恒方程[26]见式(1)。
式中i =w、j= nw或者i =nw、j= w;ρ是流体密度 (kg·m−3) ;μ是流体粘度 (Pa·s) ;Cp是比容 (Pa−1) ;k是孔隙基质的固定渗透率 (m2) ;kr是流体相的相对渗透率;u是流体达西速度 (m·s−1) ;p是流体的达西场压力 (Pa) ;g是重力加速度 (m·s−2) ;D是竖向标高 (m) 。
毛细压力 pc 通常定义为NAPL相和水相之间的压差,即式(2)。
多孔介质的孔隙空间可以完全填充为NAPL相或水相,也可以同时存在NAPL相和水相,两者有效饱和度满足式(3)。
水相比容Cpw取决于水相饱和度相对于毛细压力的变化关系,定义为式(4)。
根据式(3)和式(4)可以将NAPL相比容Cpnw定义为式(5)。
由于水相比容和NAPL相比容,仅仅相差一个负号,因此,统一定义为比容Cp。
毛细管压力、相对渗透率和相饱和度通过VAN GENUCHTEN水力本构 (式(6)~式(9)) 建立K-S-P关系[27],基于水力本构方程可以推导
$ {C_p} $ ,如式(10)。式中α、m为VG模型参数;θsw是总孔隙率或饱和体积分数;θrw是残余水相体积分数;Srw为残余水相饱和度;Sew为水相有效饱和度;ε为基质孔隙率。
孔隙-裂隙介质中裂隙部分的水相 (w) 和NAPL相 (nw) 质量守恒方程[26]见式(11)。
式中:
$ {d_f} $ 为裂隙的厚度 (m) ,$ {k_f} $ 为裂隙的渗透率 (m2) 。孔隙-裂隙介质中基质部分溶解相污染物运移方程见式(12)。
式中:Sw为水相饱和度,Sw = Srw+Sew(1‒Srw‒Srnw);Dw为水动力弥散系数 (m2·s−1) ,包括机械弥散和分子扩散,二维水动力弥散系数计算见式(13)。
式中:Dew为溶解相污染物分子扩散系数 (m2·s−1) ;αLw和αTw为溶解相污染物的纵向和横向弥散系数 (m) 。
孔隙-裂隙介质中裂隙部分溶解相污染物运移方程为式(14)。
式中:
$ {\varepsilon _f} $ 、df 、kf为裂隙部分的孔隙率、厚度和渗透率 (m2) 。孔隙-裂隙多孔介质多相抽提修复效率的评价指标是污染物去除率PR,总NAPL去除率、自由相NAPL去除率和溶解相NAPL去除率可以分别定义为式(15)~式(17)。
式中:Sn0 、Sn为NAPL相初始饱和度和终止饱和度;Sw0、Sw为水相初始饱和度和终止饱和度;C0、C是溶解相NAPL初始浓度和终止浓度 (mol·m−3) ;ρn 为NAPL相密度 (kg·m−3) ;M为NAPL相摩尔分子质量 (g·mol−1) 。
-
采用大型多物理场耦合仿真软件COMSOL MULTIPHYSICS进行求解,采用双达西定律、多孔介质中稀物质传递模块和裂隙流模块模拟饱和态低渗介质中NAPL去除。该两相流体运移模型先前已通过水气蒸发土壤干燥[28]、气相抽提[29]、热强化抽提[29]涉及的气、水两相流验证,本研究在此基础上,与HOPMANS的水、NAPL两相流试验[30]验证良好 (图1) ,验证了模型的正确性和可靠性。
-
单一水力压裂缝网采用筛口中心的水平向裂隙进行表征,本节分别模拟了筛口抽提 (仅设置基质抽提边界
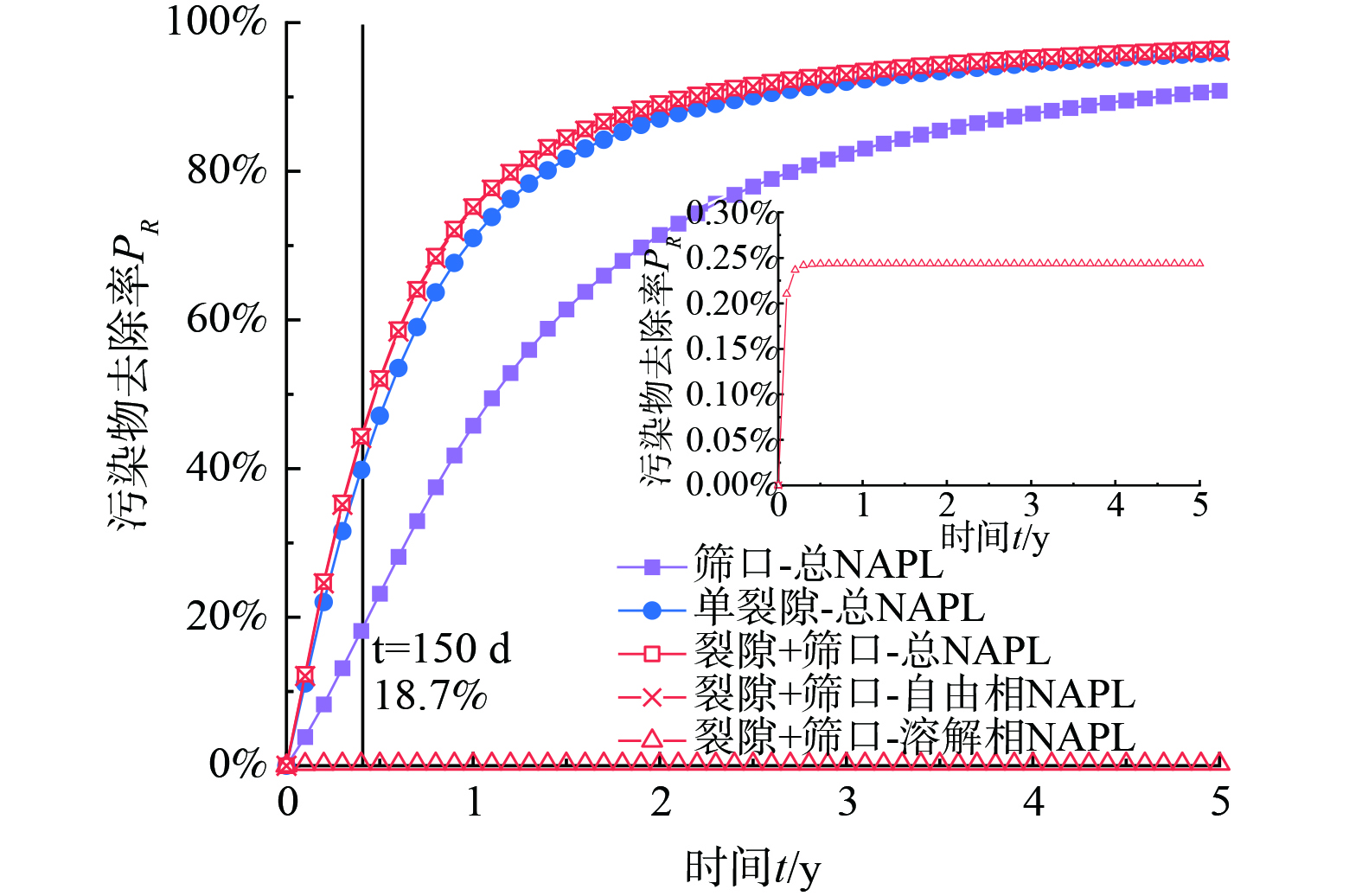
$ {q_{w0}}{\text{ }}{q_{nw0}} $ ) 、裂隙抽提 (仅设置裂隙抽提边界$ {q_{fw0}}{\text{ }}{q_{fnw0}} $ ) 、裂隙-筛口协同抽提 (同时设置基质和裂隙抽提边界) 3种工况,以修复前后场地内污染物去除率 (PR) 为评价指标,分析了压裂增渗对低渗透地层抽提效率的影响 (图3) 。可以发现,多相抽提去除主要以NAPL自由相为主,溶解相为辅,且当裂隙存在时,污染物去除率显著增大。以抽提150 d为例,筛口抽提的污染物去除率仅为18.7%,而裂隙抽提和筛口-裂隙协同抽提的去除率提高了1.2倍和1.4倍;同时,裂隙强化抽提效率主要作用于修复中前期,当修复时间为5年时,筛口抽提、裂隙抽提、筛口+裂隙抽提作用下污染物去除率分别为90.8%、95.9%、96.5%,差别不明显。 -
采用第150 d的污染物去除率表征低渗透污染场地中前期的修复效率,本节分别研究了污染程度 (Sn) 、裂缝渗透率 (kf/k) 、裂隙厚度 (df) 、裂隙长度 (Lf) 等因素的影响规律 (抽提负压为50 kPa) 。由图4可知,在单因素作用下,污染物去除率随着各自变量 (Sn、kf/k、df、Lf) 的增加而增大,变化规律均可拟合为PR = A(1‒exp(‒x/B))分布,参数A表征单因素条件下污染物的最大去除率,参数B表征单因素的影响权重。可以发现,污染程度对污染物最大去除率的影响最大,高浓度污染时去除率最大,且裂隙渗透率是影响去除效率的显著特征参数。随着裂隙渗透率的增加,污染物去除率的增加速率先快后慢,kf/k≤100时,裂隙对抽提效率的提升效果最佳。
-
本节设计了不同污染程度、裂缝渗透率、裂隙厚度、裂隙长度组合的1715组工况,综合分析了多因素共同作用下污染物去除率的变化规律。以NAPL初始饱和度为0.1为例,图5给出了裂缝特征参数对污染物去除率的耦合影响,可以发现在不同裂隙长度和裂隙渗透率条件下,增大裂隙厚度df都对污染物去除率有促进作用。同时,随着裂缝长度的增加,当裂隙渗透率kf/k≤100时污染物去除率逐渐缓慢增加;当裂隙渗透率kf/k>100时,污染物去除率呈先增加后波动降低的趋势,裂隙长度为1.5 m时效果最佳。
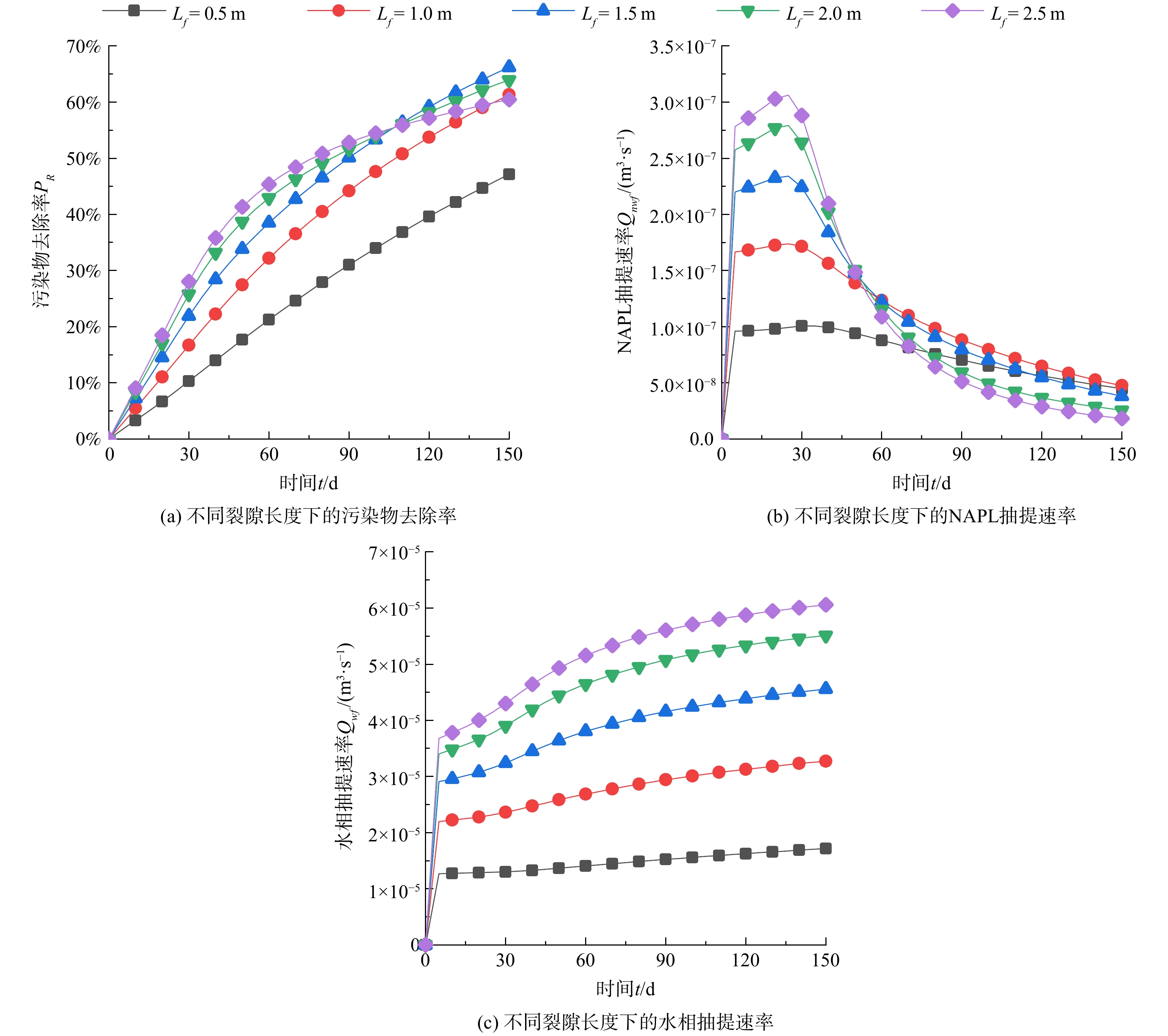
以kf/k = 1 000、df = 0.03 m为例,图6(a)进一步展示了污染物去除率随裂隙长度和修复时间的变化规律。可以发现,在修复前期 (0~40 d) ,污染物去除率的增大速率随着裂缝长度的增大而增大;但是,在修复中后期 (40~150 d) ,当裂隙长度大于1.5 m时,污染物去除率的增大速率发生减缓。图6(b)和(c)给出了裂隙口的NAPL相和水相抽提速率的变化曲线,在第40 d至60 d期间,NAPL相抽提速率发生陡降,且裂隙越长,下降越快,不同裂隙长度条件下抽提速率的大小关系发生改变;但是,水相抽提速率仍持续增大,且大小关系没有改变。因此,当裂隙长度大于1.5 m时,污染物去除率下降主要是因为NAPL抽提速率的下降和水相抽提速率的增加。由图7的NAPL相饱和度分布可知,随着修复时间逐渐从40 d增加到60 d,裂隙标高以上的NAPL相污染物逐渐减少,当裂隙长度大于1.5 m时,这部分污染物基本上被完全去除。因此,当裂隙标高上存在NAPL相污染物时,裂隙长度越长,修复效率越高,裂缝可以完全发挥作用;当裂隙标高以上的NAPL相污染物被去除后,污染物去除效率会下降,裂隙长度的优势也会被逐渐被削弱,无法完全发挥强化修复的作用。
-
1) 多相抽提去除主要以NAPL自由相为主,溶解相为辅,且当裂隙存在时,污染物去除率显著增大;同时,裂隙强化抽提效率主要作用于修复中前期。
2) 在单因素作用下,污染物去除率随着各自变量 (Sn、kf/k、df、Lf) 的增加而增大,变化规律均可拟合为PR = A(1‒exp(‒x/B))分布;污染程度对污染物最大去除率的影响最大,高浓度污染时去除率最大,且裂隙渗透率是影响去除效率的显著特征参数。
3) 在多因素耦合作用下,当裂隙渗透率kf/k大于100时,污染物去除率呈先增加后波动降低的趋势,且当裂隙长度为1.5 m时,去除效果最佳,这是因为当裂隙上层污染物被去除后,裂隙长度的促进作用会大幅衰减。因此,当裂隙设置于污染地层的下部,更有利于污染物的去除。
压裂缝网特征对低渗透NAPL污染地层抽提效率的影响机制
Mechanism of fracture network characteristics on extraction efficiency in low-permeability NAPL-contaminated formations
-
摘要: 水力压裂可以有效改善低渗透污染地层物质传输速率低的难题,提升修复效率。采用大型多物理场耦合仿真软件COMSOL MULTIPHYSICS模拟低渗污染地层压裂协同抽提修复,分析不同压裂缝网特征对低渗透非水相液体 (NAPLs) 污染地层抽提效率的影响机制。结果表明,压裂缝网可以有效提升抽提效率,模拟工况的提升率可达42%,且污染物去除率均随着裂隙厚度、长度和渗透率的增加而提高,裂隙渗透率是最主要的影响因素。通过缝网特征参数的耦合分析发现,当裂隙渗透率kf/k大于100时,污染物去除率呈先增加后波动降低的趋势,且当裂隙长度为1.5 m时,去除效果最佳,这是因为当裂隙上层污染物被去除后,裂隙长度的促进作用会大幅衰减。因此,当裂隙设置于污染地层的下部,更有利于污染物的去除。Abstract: Hydraulic fracturing, which can improve substance transport, offers an effective solution to the challenge of remediating low-permeability contaminated formations. This study employed COMSOL Multiphysics, a large-scale multi-physics coupled simulation software, to simulate hydraulic fracturing-assisted extraction of non-aqueous phase liquids (NAPLs) in low permeability formations. The influence of different fracture network characteristics on the extraction efficiency was analyzed. The results demonstrate that the extraction efficiency can be significantly enhanced by the fracture network, with an improvement rate over 42% and the removal rate of pollutants increases with fracture thickness, length, and permeability, with the fracture permeability being the primary influencing factor. Through coupling analysis of fracture network parameters, it was observed that when the ratio of fracture permeability (kf) to matrix permeability (k) exceeds 100, the removal rate of pollutants initially increases, then fluctuates before declining. Additionally, the optimal removal effect was achieved with a fracture length of 1.5 m. This phenomenon can be attributed to the substantial attenuation of the promoting effect of fracture length after the removal of pollutants from the upper layer of the fracture. Hence, locating the fracture network in the lower part of the contaminated formation is more advantageous for pollutant removal.
-
Key words:
- low-permeability /
- contaminated formations /
- fracture network /
- NAPL /
- extraction
-
随着我国工业化和城镇化进程的加速发展,工业结构调整和空间格局重构导致大批污染企业搬迁、改造或关闭,在城市及其周边地区遗留千万公顷污染场地,严重威胁居民健康和环境安全[1-4]。由于氯代烃、石油烃等有机污染物的溶解度较低,通常以非水相液体 (NAPLs) 存在于地下土水环境中并迁移形成污染羽。当存在有低渗透地层时,会在低渗透地层上形成污染池,并通过扩散作用或者天然裂隙侵入低渗透地层,形成持久性污染源[5]。现有抽提、氧化等原位修复技术[6-8]可以有效修复低渗透介质层上的污染池,但受限于物质传输速率,低渗透介质内的污染物难以被去除,导致修复反弹[5, 9-10]。因此,低渗透污染地层的修复是当前污染场地修复的重大挑战。
为了提升低渗透污染地层的渗透性,可以引入石油开采行业的压裂技术形成缝网结构,提升物质传输速率[11-13],与多相抽提技术形成协同工作模式,实现高效去除[14-16]。目前,国内外学者已针对压裂协同抽提修复技术开展了一系列研究。MURDOCH等[17]以未压裂抽提井为空白对照,设置2个压裂抽提井,发现压裂前后抽提流量提高了13~31倍,随着流动相和非流动相之间物质传质速率的增大,污染物去除率提高675%[18],论证了水力压裂与抽提协同的有效性。为了进一步揭示压裂对气相抽提的影响机制,SCHULENBERG和REEVES[19]建立了压裂协同气相抽提轴对称模型,发现裂隙长度对污染物去除率的敏感性不如裂隙渗透率;CHEN等[20]利用TMVOC代码和MINC方法,建立了双孔隙介质压裂协同热强化抽提数值模型,同样发现基质渗透率的敏感性远大于抽提压力、裂隙间距和孔径;BRANDNER和MURDOCH[21]利用数值模型,参考石油行业开采井的标量评价指标流动速率,定义裂隙有效流通率,量化评价裂隙对污染物去除率的影响。在试验方面,TZOVOLOU等[22]以砂层等效水力压裂裂缝,利用模型试验论证了裂缝中对蒸汽修复效率的强化作用,去除率可达77%,同时他们也在现场试验中论证了压裂协同生物通风修复低渗透污染土的技术有效性和经济性[23]。针对埋深9~12 m的污染低渗冰川土,CUSHMAN等[24]通过试验发现压裂后的多相抽提效率是压裂前的6倍;NILSSON等[25]则通过低渗污染场地的压裂协同抽提中试试验,发现气/水/非水相污染物均被负压抽提,而总NAPL的质量去除率达到30%。虽然,目前污染场地的压裂协同抽提修复的技术有效性均得到了试验和数值仿真的论证,但是现有研究仍主要以尝试为主,并将污染物去除率作为主要评价指标,缺乏对压裂增渗强化污染物去除机理的深入研究,特别是孔隙-裂隙介质中的优势渗流规律。
为此,本研究首先建立孔隙-裂隙介质中多相抽提数值模型,利用COMSOL MULTIPHYSICS软件进行求解,以低渗透污染地层污染程度、压裂缝网特征参数 (裂隙长度、厚度和渗透率) 开展单因素和多因素参数化分析,探究压裂缝网对低渗透NAPL污染地层多相抽提效率的影响机制。
1. 孔隙-裂隙介质中多相抽提数学模型
1.1 数学模型的建立
饱和态孔隙-裂隙介质的多相抽提主要涉及2个过程,一是抽提作用下自由相和水相迁移,二是溶解相对流-弥散作用,由于自由相的浓度远高于溶解相,本研究主要考虑自由相污染物去除,因此忽略污染物的相间传质,并假设地层中初始污染物均匀分布。模型控制方程由孔隙介质与裂隙介质中的水相和NAPL相质量守恒方程、水力本构方程、溶解相污染物运移方程组成。
孔隙-裂隙介质中基质部分的水相 (w) 和NAPL相 (nw) 质量守恒方程[26]见式(1)。
$stringUtils.convertMath($!{formula.content}) $ (1) $ 式中i =w、j= nw或者i =nw、j= w;ρ是流体密度 (kg·m−3) ;μ是流体粘度 (Pa·s) ;Cp是比容 (Pa−1) ;k是孔隙基质的固定渗透率 (m2) ;kr是流体相的相对渗透率;u是流体达西速度 (m·s−1) ;p是流体的达西场压力 (Pa) ;g是重力加速度 (m·s−2) ;D是竖向标高 (m) 。
毛细压力 pc 通常定义为NAPL相和水相之间的压差,即式(2)。
$stringUtils.convertMath($!{formula.content}) $ (2) $ 多孔介质的孔隙空间可以完全填充为NAPL相或水相,也可以同时存在NAPL相和水相,两者有效饱和度满足式(3)。
$stringUtils.convertMath($!{formula.content}) $ (3) $ 水相比容Cpw取决于水相饱和度相对于毛细压力的变化关系,定义为式(4)。
$stringUtils.convertMath($!{formula.content}) $ (4) $ 根据式(3)和式(4)可以将NAPL相比容Cpnw定义为式(5)。
$stringUtils.convertMath($!{formula.content}) $ (5) $ 由于水相比容和NAPL相比容,仅仅相差一个负号,因此,统一定义为比容Cp。
毛细管压力、相对渗透率和相饱和度通过VAN GENUCHTEN水力本构 (式(6)~式(9)) 建立K-S-P关系[27],基于水力本构方程可以推导
$ {C_p} $ $stringUtils.convertMath($!{formula.content}) $ (6) $ $stringUtils.convertMath($!{formula.content}) $ (7) $ $stringUtils.convertMath($!{formula.content}) $ (8) $ $stringUtils.convertMath($!{formula.content}) $ (9) $ $stringUtils.convertMath($!{formula.content}) $ (10) $ 式中α、m为VG模型参数;θsw是总孔隙率或饱和体积分数;θrw是残余水相体积分数;Srw为残余水相饱和度;Sew为水相有效饱和度;ε为基质孔隙率。
孔隙-裂隙介质中裂隙部分的水相 (w) 和NAPL相 (nw) 质量守恒方程[26]见式(11)。
$stringUtils.convertMath($!{formula.content}) $ (11) $ 式中:
$ {d_f} $ $ {k_f} $ 孔隙-裂隙介质中基质部分溶解相污染物运移方程见式(12)。
$stringUtils.convertMath($!{formula.content}) $ (12) $ 式中:Sw为水相饱和度,Sw = Srw+Sew(1‒Srw‒Srnw);Dw为水动力弥散系数 (m2·s−1) ,包括机械弥散和分子扩散,二维水动力弥散系数计算见式(13)。
$stringUtils.convertMath($!{formula.content}) $ (13) $ 式中:Dew为溶解相污染物分子扩散系数 (m2·s−1) ;αLw和αTw为溶解相污染物的纵向和横向弥散系数 (m) 。
孔隙-裂隙介质中裂隙部分溶解相污染物运移方程为式(14)。
$stringUtils.convertMath($!{formula.content}) $ (14) $ 式中:
$ {\varepsilon _f} $ 孔隙-裂隙多孔介质多相抽提修复效率的评价指标是污染物去除率PR,总NAPL去除率、自由相NAPL去除率和溶解相NAPL去除率可以分别定义为式(15)~式(17)。
$stringUtils.convertMath($!{formula.content}) $ (15) $ $stringUtils.convertMath($!{formula.content}) $ (16) $ $stringUtils.convertMath($!{formula.content}) $ (17) $ 式中:Sn0 、Sn为NAPL相初始饱和度和终止饱和度;Sw0、Sw为水相初始饱和度和终止饱和度;C0、C是溶解相NAPL初始浓度和终止浓度 (mol·m−3) ;ρn 为NAPL相密度 (kg·m−3) ;M为NAPL相摩尔分子质量 (g·mol−1) 。
1.2 数学模型的求解
采用大型多物理场耦合仿真软件COMSOL MULTIPHYSICS进行求解,采用双达西定律、多孔介质中稀物质传递模块和裂隙流模块模拟饱和态低渗介质中NAPL去除。该两相流体运移模型先前已通过水气蒸发土壤干燥[28]、气相抽提[29]、热强化抽提[29]涉及的气、水两相流验证,本研究在此基础上,与HOPMANS的水、NAPL两相流试验[30]验证良好 (图1) ,验证了模型的正确性和可靠性。
2. 孔隙-裂隙介质多相抽提模型及基本参数
2.1 模型设置与初始值、边界条件
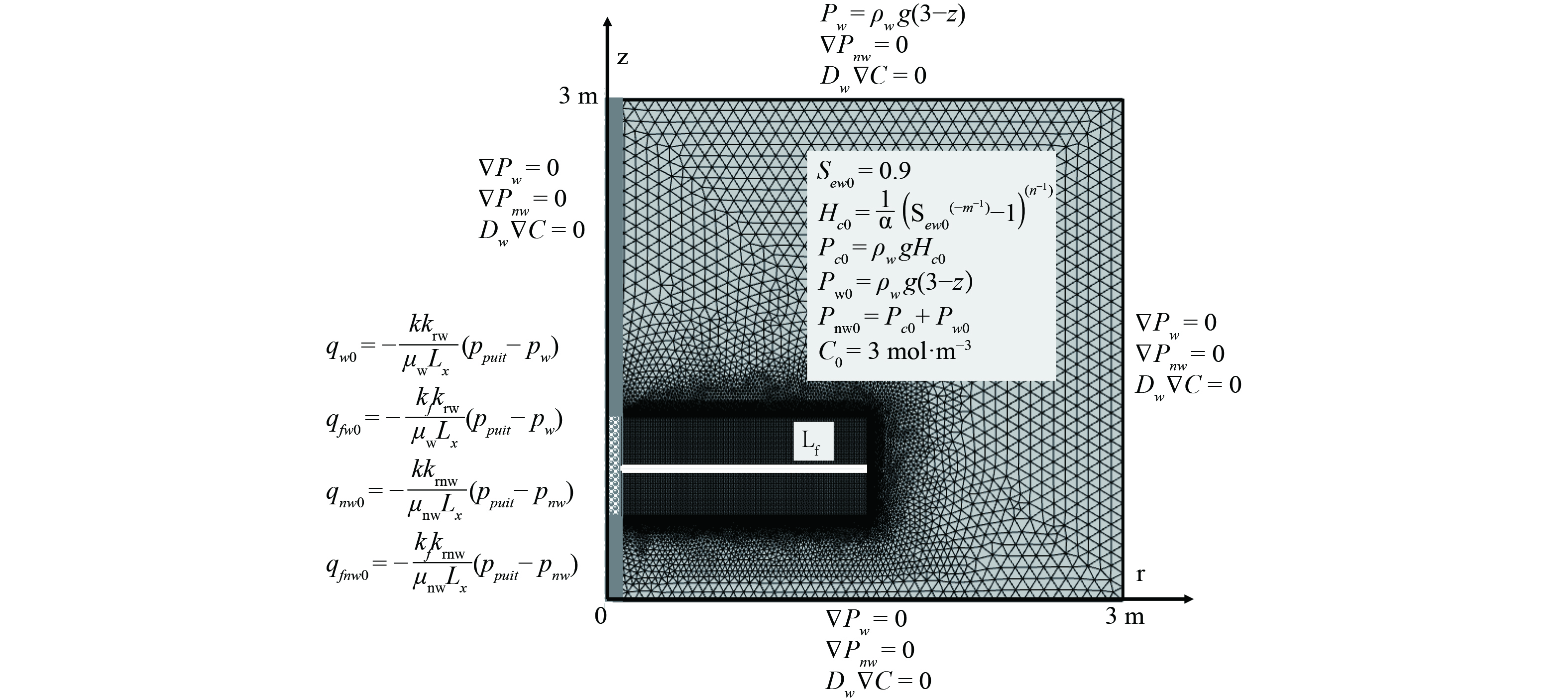
含水层中低渗污染土压裂协同抽提修复的概化模型如图2所示,模拟尺寸为3 m×3 m,是以抽提井管为中轴线的二维轴对称模型,井管筛口处施加负压并在中心位置生成水平向裂隙。图2也详细介绍了水相达西场、NAPL相达西场、溶解相传递场的初始值和边界条件。
2.2 模型基本参数
模型中采用的参数值,如表1所示,包括土壤、水和NAPL的特征参数。
表 1 模型相关参数Table 1. Parameters used in the numerical model模型参数名称 符号 取值 单位 土体孔隙率 $ \varepsilon $ 0.32 1 土体固有渗透率 $ k $ 1×10−13 m2 土体干密度 $ \rho $ 1 600 kg·m−3 水的密度 $ {\rho _{\text{w}}} $ 1 000 kg·m−3 水的粘度 $ {\mu _w} $ 1×10−3 Pa·s 水的残余饱和度 $ {S_{rw}} $ 0.007 2 1 NAPL的密度 $ {\rho _{nw}} $ 1 460 kg·m−3 NAPL的粘度 $ {\mu _{{\text{n}}w}} $ 5.8×10−3 Pa·s NAPL的相对分子质量 M 131 g·mol−1 NAPL的残余饱和度[31] $ {S_{rnw}} $ 0 1 NAPL溶解相分子扩散系数[32] $ D_e^w $ 1.31×10−6 cm2·s−1 NAPL溶解相的纵向弥散系数 $ \alpha _L^w $ 0.5 m NAPL溶解相的横向弥散系数 $ \alpha _T^w $ 0.05 m K-S-P本构参数 $ \alpha $ 3.58 m−1 K-S-P本构参数 l 0.5 1 K-S-P本构参数 n 3.136 5 1 K-S-P本构参数 m 1-1/n 1 裂隙的孔隙率 $ {\varepsilon _f} $ 0.5 1 裂隙的固有渗透率 $ {k_f}/k $ 100 1 裂隙的厚度 $ {d_f} $ 0.03 m 裂隙的长度 $ {L_f} $ 1.5 m 抽提压力 $ {p_{puit}} $ −50 kPa 筛口过滤的等效流动阻力[16] $ {L_x} $ 5 cm 3. 孔隙-裂隙介质多相抽提规律与讨论
3.1 压裂增渗对污染物去除率的影响
单一水力压裂缝网采用筛口中心的水平向裂隙进行表征,本节分别模拟了筛口抽提 (仅设置基质抽提边界
$ {q_{w0}}{\text{ }}{q_{nw0}} $ $ {q_{fw0}}{\text{ }}{q_{fnw0}} $ 3.2 裂缝特征参数单因素分析
采用第150 d的污染物去除率表征低渗透污染场地中前期的修复效率,本节分别研究了污染程度 (Sn) 、裂缝渗透率 (kf/k) 、裂隙厚度 (df) 、裂隙长度 (Lf) 等因素的影响规律 (抽提负压为50 kPa) 。由图4可知,在单因素作用下,污染物去除率随着各自变量 (Sn、kf/k、df、Lf) 的增加而增大,变化规律均可拟合为PR = A(1‒exp(‒x/B))分布,参数A表征单因素条件下污染物的最大去除率,参数B表征单因素的影响权重。可以发现,污染程度对污染物最大去除率的影响最大,高浓度污染时去除率最大,且裂隙渗透率是影响去除效率的显著特征参数。随着裂隙渗透率的增加,污染物去除率的增加速率先快后慢,kf/k≤100时,裂隙对抽提效率的提升效果最佳。
3.3 裂缝特征参数多因素分析
本节设计了不同污染程度、裂缝渗透率、裂隙厚度、裂隙长度组合的1715组工况,综合分析了多因素共同作用下污染物去除率的变化规律。以NAPL初始饱和度为0.1为例,图5给出了裂缝特征参数对污染物去除率的耦合影响,可以发现在不同裂隙长度和裂隙渗透率条件下,增大裂隙厚度df都对污染物去除率有促进作用。同时,随着裂缝长度的增加,当裂隙渗透率kf/k≤100时污染物去除率逐渐缓慢增加;当裂隙渗透率kf/k>100时,污染物去除率呈先增加后波动降低的趋势,裂隙长度为1.5 m时效果最佳。
以kf/k = 1 000、df = 0.03 m为例,图6(a)进一步展示了污染物去除率随裂隙长度和修复时间的变化规律。可以发现,在修复前期 (0~40 d) ,污染物去除率的增大速率随着裂缝长度的增大而增大;但是,在修复中后期 (40~150 d) ,当裂隙长度大于1.5 m时,污染物去除率的增大速率发生减缓。图6(b)和(c)给出了裂隙口的NAPL相和水相抽提速率的变化曲线,在第40 d至60 d期间,NAPL相抽提速率发生陡降,且裂隙越长,下降越快,不同裂隙长度条件下抽提速率的大小关系发生改变;但是,水相抽提速率仍持续增大,且大小关系没有改变。因此,当裂隙长度大于1.5 m时,污染物去除率下降主要是因为NAPL抽提速率的下降和水相抽提速率的增加。由图7的NAPL相饱和度分布可知,随着修复时间逐渐从40 d增加到60 d,裂隙标高以上的NAPL相污染物逐渐减少,当裂隙长度大于1.5 m时,这部分污染物基本上被完全去除。因此,当裂隙标高上存在NAPL相污染物时,裂隙长度越长,修复效率越高,裂缝可以完全发挥作用;当裂隙标高以上的NAPL相污染物被去除后,污染物去除效率会下降,裂隙长度的优势也会被逐渐被削弱,无法完全发挥强化修复的作用。
4. 结论
1) 多相抽提去除主要以NAPL自由相为主,溶解相为辅,且当裂隙存在时,污染物去除率显著增大;同时,裂隙强化抽提效率主要作用于修复中前期。
2) 在单因素作用下,污染物去除率随着各自变量 (Sn、kf/k、df、Lf) 的增加而增大,变化规律均可拟合为PR = A(1‒exp(‒x/B))分布;污染程度对污染物最大去除率的影响最大,高浓度污染时去除率最大,且裂隙渗透率是影响去除效率的显著特征参数。
3) 在多因素耦合作用下,当裂隙渗透率kf/k大于100时,污染物去除率呈先增加后波动降低的趋势,且当裂隙长度为1.5 m时,去除效果最佳,这是因为当裂隙上层污染物被去除后,裂隙长度的促进作用会大幅衰减。因此,当裂隙设置于污染地层的下部,更有利于污染物的去除。
-
表 1 模型相关参数
Table 1. Parameters used in the numerical model
模型参数名称 符号 取值 单位 土体孔隙率 $ \varepsilon $ 0.32 1 土体固有渗透率 $ k $ 1×10−13 m2 土体干密度 $ \rho $ 1 600 kg·m−3 水的密度 $ {\rho _{\text{w}}} $ 1 000 kg·m−3 水的粘度 $ {\mu _w} $ 1×10−3 Pa·s 水的残余饱和度 $ {S_{rw}} $ 0.007 2 1 NAPL的密度 $ {\rho _{nw}} $ 1 460 kg·m−3 NAPL的粘度 $ {\mu _{{\text{n}}w}} $ 5.8×10−3 Pa·s NAPL的相对分子质量 M 131 g·mol−1 NAPL的残余饱和度[31] $ {S_{rnw}} $ 0 1 NAPL溶解相分子扩散系数[32] $ D_e^w $ 1.31×10−6 cm2·s−1 NAPL溶解相的纵向弥散系数 $ \alpha _L^w $ 0.5 m NAPL溶解相的横向弥散系数 $ \alpha _T^w $ 0.05 m K-S-P本构参数 $ \alpha $ 3.58 m−1 K-S-P本构参数 l 0.5 1 K-S-P本构参数 n 3.136 5 1 K-S-P本构参数 m 1-1/n 1 裂隙的孔隙率 $ {\varepsilon _f} $ 0.5 1 裂隙的固有渗透率 $ {k_f}/k $ 100 1 裂隙的厚度 $ {d_f} $ 0.03 m 裂隙的长度 $ {L_f} $ 1.5 m 抽提压力 $ {p_{puit}} $ −50 kPa 筛口过滤的等效流动阻力[16] $ {L_x} $ 5 cm -
[1] 环境保护部, 国土资源部. 全国土壤污染状况调查公报[R], 2014. [2] GE F, ZHANG Z X, FU H, et al. Distribution of organic contaminated sites in china: Statu quo and prospect[J]. Soils, 2021, 53(6): 1132-1141. [3] LUO Y M, TENG Y. Research progresses and prospects on soil pollution and remediation in china[J]. Acta Pedologica Sinica, 2020, 57(5): 1137-1142. [4] 刘松玉, 詹良通, 胡黎明, 等. 环境岩土工程研究进展[J]. 土木工程学报, 2016, 49(3): 6-30. [5] YOU X J, LIU S G, DAI C M, et al. Contaminant occurrence and migration between high- and low-permeability zones in groundwater systems: A review[J]. Science of the Total Environment, 2020, 743: 140703. doi: 10.1016/j.scitotenv.2020.140703 [6] SOOKHAK LARI K, RAYNER J L, DAVIS G B. Toward optimizing LNAPL remediation[J]. Water Resources Research, 2019, 55(2): 923-936. doi: 10.1029/2018WR023380 [7] HAN C, ZHU X B, XIONG G Y, et al. Quantitative study of in situ chemical oxidation remediation with coupled thermal desorption[J]. Water Research, 2023, 239: 120035. doi: 10.1016/j.watres.2023.120035 [8] LI Y, WEI M L, YU B W, et al. Thermal desorption optimization for the remediation of hydrocarbon-contaminated soils by a self-built sustainability evaluation tool[J]. Journal of Hazardous Materials, 2022, 436: 129156. doi: 10.1016/j.jhazmat.2022.129156 [9] YANG M, ANNABLE M D, JAWITZ J W. Back diffusion from thin low permeability zones[J]. Environmental Science & Technology, 2015, 49(1): 415-422. [10] ZHAO S, ZHANG J, FENG S J. The era of low-permeability sites remediation and corresponding technologies: A review[J]. Chemosphere, 2023, 313: 137264. doi: 10.1016/j.chemosphere.2022.137264 [11] MURDOCH L C. Hydraulic fracturing of soil during laboratory experiments part 1. Methods and observations[J]. Geotechnique 1992, 43(2): 255-265. [12] MURDOCH L C. Hydraulic fracturing of soil during laboratory experiments part 2. Propagation[J]. Geotechnique 1993, 43(2): 267-276. [13] MURDOCH L C. Hydraulic fracturing of soil during laboratory experiments part 3. Theoretical analysis[J]. Geotechnique 1993, 43(2): 277-287. [14] SHEN J, YAN J, GAO W, et al. Application potential of multi-phase extraction technology in remediations of chemical contaminated sites[J]. Chinese Journal of Environmental Engineering, 2021, 15(10): 3286-3296. [15] QI S Q, LUO J, O'CONNOR D, et al. A numerical model to optimize LNAPL remediation by multi-phase extraction[J]. Science of the Total Environment, 2020, 718: 137309. [16] KACEM M, BENADDA B. Mathematical model for multiphase extraction simulation[J]. Journal of Environmental Engineering, 2018, 144(6): 04018040. doi: 10.1061/(ASCE)EE.1943-7870.0001378 [17] MURDOCH L, KEMPER M, NARAYANASWAMY M, et al. Demonstration of hydraulic fracturing to facilitate remediation[R]. United States: Hazardous Waste Research and Information Center (HWRIC), 1994. [18] SKOVRONEK H S. Accutech pneumatic fracturing extraction and hot gas injection, phase 1. Applications analysis report[R]. United States: Environmental Protection Agency, 1993. [19] SCHULENBERG J W, REEVES H W. Axi-symmetric simulation of soil vapor extraction influenced by soil fracturing[J]. Journal of Contaminant Hydrology, 2002, 57(3-4): 189-222. doi: 10.1016/S0169-7722(02)00003-7 [20] CHEN F, FALTA R W, MURDOCH L C. Numerical analysis of thermal remediation in 3D field-scale fractured geologic media[J]. Groundwater, 2015, 53(4): 572-587. doi: 10.1111/gwat.12241 [21] BRADNER G C, MURDOCH L C. Effects of skin and hydraulic fractures on SVE wells[J]. Journal of Contaminant Hydrology, 2005, 77(4): 271-297. doi: 10.1016/j.jconhyd.2005.02.001 [22] TZOVOLOU D N, AGGELOPOULOS C A, THEODOROPOULOU M A, et al. Remediation of the unsaturated zone of NAPL-polluted low permeability soils with steam injection: An experimental study[J]. Journal of Soils and Sediments, 2011, 11(1): 72-81. doi: 10.1007/s11368-010-0268-5 [23] TZOVOLOU D N, THEODOROPOULOU M A, BLANCHET D, et al. In situ bioventing of the vadose zone of multi-scale heterogeneous soils[J]. Environmental Earth Sciences, 2015, 74(6): 4907-4925. doi: 10.1007/s12665-015-4501-9 [24] CUSHMAN D J, HARE R W. Remediation of deep LNAPL from glacial soils using high n back to remtech vacuum multi-phase extraction (MPE), pneumatic air lift (PAL), and pneumatic fracturing (PF); [C]// Remediation Technologies Symposium, Canada, 2005, 67-81. [25] NILSSON B. Combining steam injection with hydraulic fracturing for the in situ remediation of the unsaturated zone of a fractured soil polluted by jet fuel[J]. Journal of Environmental Management, 2011, 92(3): 695-707. doi: 10.1016/j.jenvman.2010.10.004 [26] TOUMA J, VAUCLIN M. Experimental and numerical analysis of two-phase infiltration in a partially saturated soil[J]. Transport in Porous Media, 1986, 1(1): 27-55. doi: 10.1007/BF01036524 [27] VANGENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898. doi: 10.2136/sssaj1980.03615995004400050002x [28] ZHENG Q T, YANG C B X, FENG S J, et al. Numerical modeling of drying from saturated to unsaturated conditions with two-phase partitioning boundaries at the medium surface and interface-dependent phase change[J]. International Journal of Multiphase Flow, 2024, 171: 104671. doi: 10.1016/j.ijmultiphaseflow.2023.104671 [29] ZHENG Q T, YANG C B X, FENG S J, et al. Influence mechanism of thermally enhanced phase change on heat transfer and soil vapour extraction[J]. Journal of Contaminant Hydrology, 2023, 257: 104202. doi: 10.1016/j.jconhyd.2023.104202 [30] CHEN J, HOPMANS J W, GRISMER M E. Parameter estimation of two-fluid capillary pressure–saturation and permeability functions[J]. Advances in Water Resources, 1999, 22(5): 479-493. doi: 10.1016/S0309-1708(98)00025-6 [31] 田蕾, 胡立堂, 张梦琳. 低渗透石化污染场地多相抽提修复效率的数值模拟[J]. 中国环境科学, 2022, 42(2): 925-935. [32] AYRAL-CINAR D, DEMOND A H. Effective diffusion coefficients of dnapl waste components in saturated low permeability soil materials[J]. Journal of Contaminant Hydrology, 2017, 207: 1-7. doi: 10.1016/j.jconhyd.2017.09.008 -











 下载:
下载: