-
目前，我国每年生活垃圾无害化处理已超过24×108 t[1]，卫生填埋是现阶段处理城市固体废弃物的主要手段之一[2]。膨润土衬垫(Geosynthetic Clay Liner，GCL)由2层土工织物夹裹1层膨润土构成，是我国目前新建和扩建卫生填埋场的关键防渗材料[3-5]。垃圾渗沥液在GCL中的扩散和运移过程是个复杂的多场耦合问题，受无机盐化学溶质和垃圾体上覆应力作用影响显著[6]。同时，GCL的渗透特性和结构性演化会相互影响，形成互馈机制[7]。填埋场服役过程中，GCL的渗透破坏不仅是化学和应力等多种外界复杂地质环境因素共同作用的结果，而且是渗沥液迁移过程中膨润土结构性演化的结果[8-9]。因此，开展耦合效应下GCL的扩散行为分析，对于正确评估GCL的防渗性能具有重要的理论价值。
针对GCL防渗性能的研究主要集中在实验测试方面[10-14]。结果表明，GCL中，起主要防渗作用的材料是膨润土，上覆应力和化学离子的扩散行为会直接影响GCL的防渗性能[15-17]。MALUSIS等[18]研究了Cl−和K+在GCL中的扩散行为，分析了离子浓度和上覆应力对扩散行为的影响。但是，由于观测手段的限制，实验难于直接观测溶质在GCL中的扩散过程[18]。ASHMAWY等[19]研究了Cl−、Na+、K+、Ca2+和Mg2+在GCL中的扩散行为，分析了离子浓度和孔隙比的影响。何俊等[20]以Cl−、Ca2+、Zn2+作为垃圾渗沥液的典型污染物，研究了其在GCL中的扩散行为。目前，就渗沥液水头[21-23]、垃圾堆体上覆应力[24-26]以及化学溶质[27-30]复杂耦合条件下GCL溶质扩散行为的研究非常匮乏[31]。
数值模拟是研究多孔介质水力特性的主要手段之一[32]。其中，COMSOL Multiphysics在分析多物理场耦合以及在溶质扩散和流体渗流等复杂问题方面具有明显的优势[33]。采用COMSOL Multiphysics软件，构建膨润土扩散柱的数值模型，以研究不同溶质浓度和不同离子种类的扩散速率和扩散规律，分析水头压力及上覆应力等因素对GCL中溶质扩散行为的影响，并提出渗透系数与扩散系数之间的计算公式，以期为GCL在填埋场中的工程应用和防污安全预警提供参考。
-
COMSOL Multiphysics以有限元为基础，通过求解偏微分方程(单场)和方程组(多场)实现多场耦合的仿真模拟[34]，其建模过程一般分为基本假设及几何模型建立、确定物理场控制方程并赋予物理场、网格划分及求解3部分。
-
依据已有研究[10,35-36]，考虑GCL孔隙率和扩散系数的影响，同时考虑美国材料与试验协会GCL系列测试标准(ASTM D6766)[37]中膨润土基本达到饱和状态等条件，本研究数值模型建立的基本假设为：GCL为均一饱和介质，离子扩散与流体渗透具有相同曲折度，流体渗流满足达西定律。
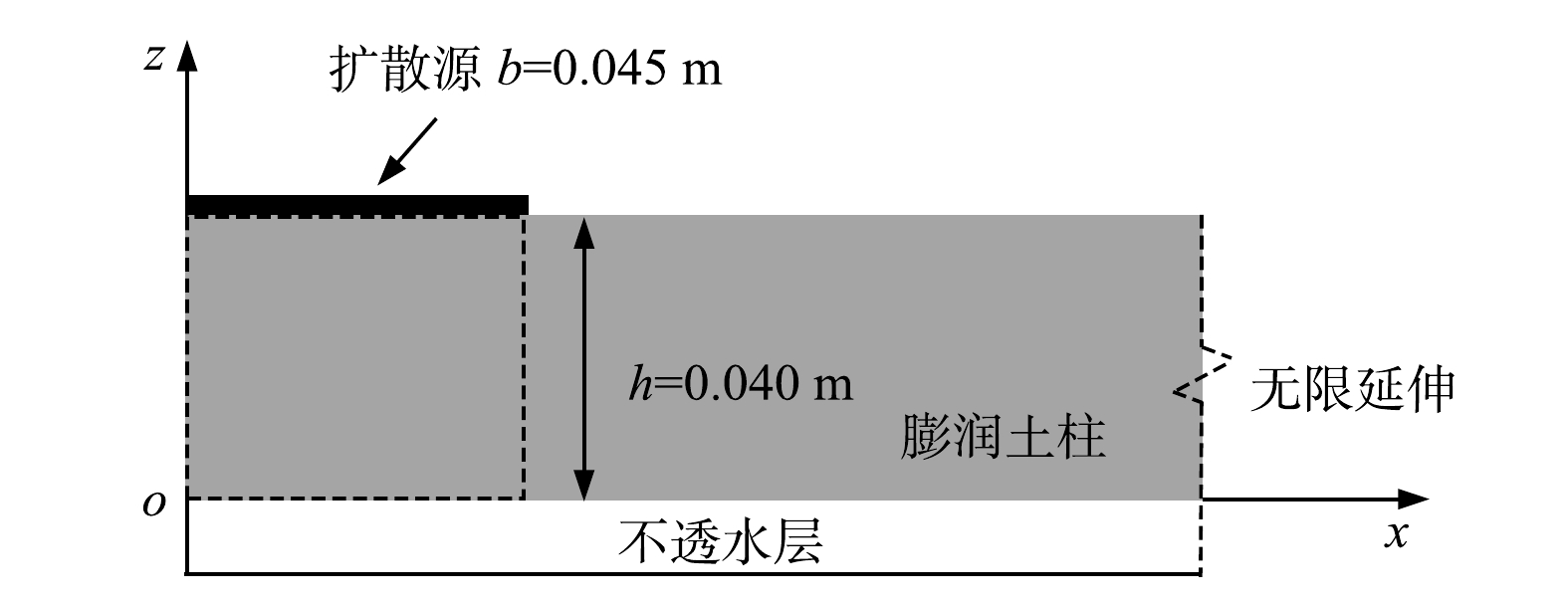
基于膨润土扩散柱实验[38]，同时考虑边界无限延伸的工程实际，采用图1所示膨润土模拟扩散柱。其中，模型上边界和下边界设为沿x方向扩展的无限边界，上边界为膨润土柱上表面，下边界为不透水层边界。膨润土柱z方向上的高度h为0.040 m，扩散源宽度b为0.045 m(图1矩形虚线框所示)。初始扩散源均匀分布在图1箭头所示平面位置。
-
质量守恒时，单位体积多孔介质的浓度随时间的变化量可以用扩散项、对流项、吸附项、源项与衰变项等表示见式(1) [39]。
式中：θl为体积含水量，表示为非饱和土的含水率；C为溶质浓度，mol∙m−3；
∇(θlDeff∇C) 表示为单位体积多孔介质内受扩散系数影响随浓度变化的扩散项；u∇C 为流速场和浓度梯度引起的对流场，u为达西流速，m∙s−1；∂∂t(ρdCs) 为受干密度影响的溶质吸附项；qCR为源项，q为单位体积流入的源体体积流量，1∙s−1；CR是源体的浓度，mol∙m−3；ζ1和ζ2分别表示为物质在过程中发生反应降解和衰变的速率，mol∙m−2∙s−1。当GCL内膨润土基本达到饱和时，式(1)左侧的θl C随时间的变化率见式(2)。
求解过程中溶质质量守恒且无外部溶质流入，则有
q=∂θl∂t 。同时，考虑模型假设GCL为连续介质，微元体内有CR=C。因此，qCR如式(3)所示。由于渗流过程温度恒定，同时多孔介质GCL为基本饱和状态，其孔隙率基本不发生变化，因此，溶质不发生衰变且有θl=n。将式(2)和式(3)代入式(1)，则得到控制溶质浓度扩散的非稳态扩散连续性方程如式(4)所示。
-
Cl−、Ca2+、Zn2+是常见的垃圾填埋场渗沥液所包含的离子，参考扩散柱实验结果[38]，本研究选择CaCl2、ZnSO4为初始扩散源溶质，研究化学溶质在GCL中的扩散行为，具体参数汇总如表1所示。参考已有实验数据[20,40-42]，选定模型中Cl−、Ca2+、Zn2+的扩散系数如表2所示。
-
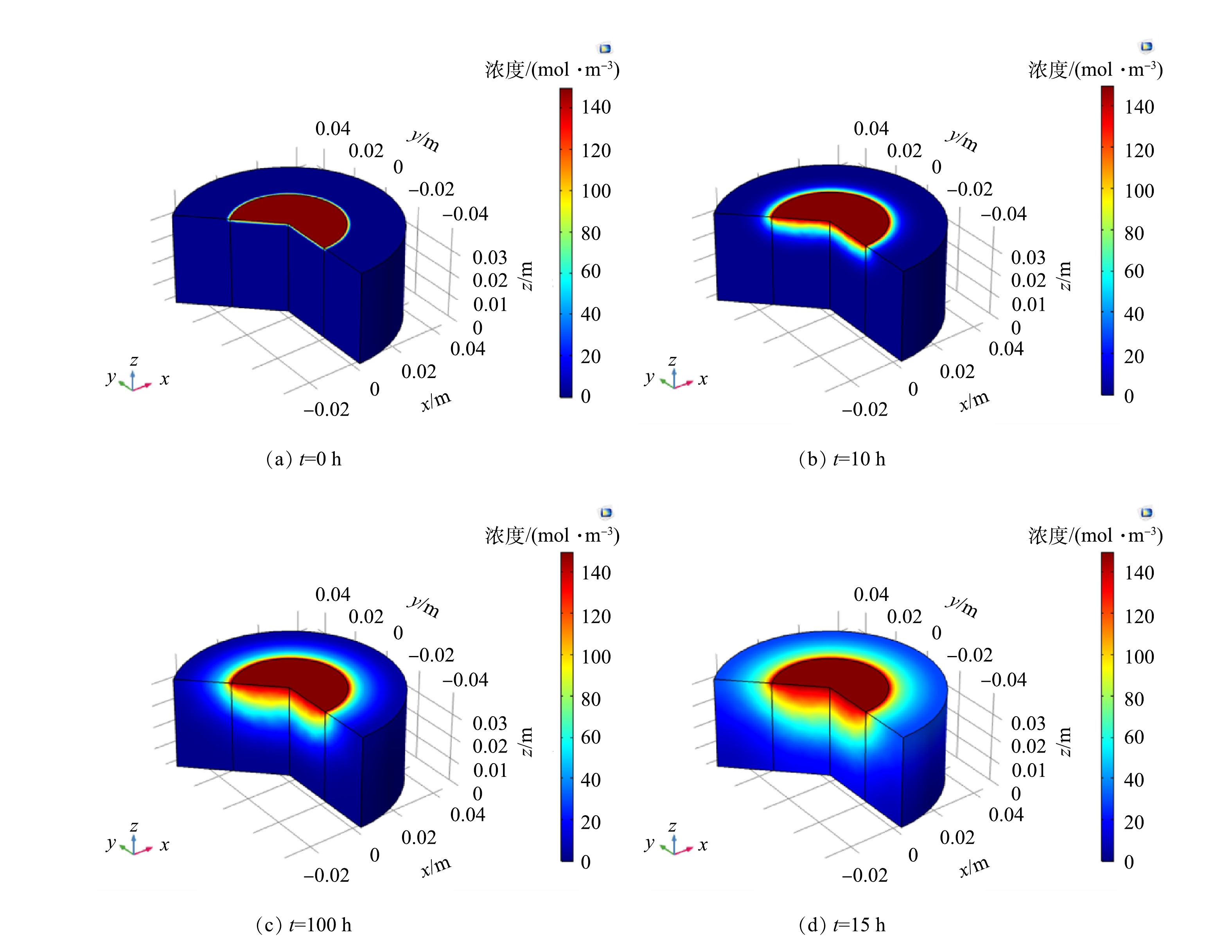
图2所示为Ca2+在不同时刻的扩散浓度分布图。比较图2(a)至2(d)可以看出，由于模型假设了GCL为均匀介质，因此Ca2+浓度分别在
3个方向是均匀扩散的。但是，Ca2+在竖直方向(z方向)的扩散速率明显大于水平方向的(x和y方向)。这是因为竖直方向为流体渗流方向，同时，溶质浓度随化学溶质的扩散会产生一定梯降，该梯降会加速GCL由均匀介质向非均匀介质转换，最终使得Ca2+在竖直方向的扩散速率最大。此外，比较图2(a)至2(d)可以看出，Ca2+浓度的扩散速度随时间的增长而逐渐减小。以Ca2+扩散浓度达到60 mol∙m−3时为例，10、100、150 h后，Ca2+运移的深度分别为0.005、0.015、0.02 m，对应的Ca2+平均运移速度分别为0.005、1.5×10−4、1.3×10−4 m∙h−1。此外，从t=0 h至t=100 h时间内，Ca2+扩散浓度随深度变化较大。但是，在t=100 h至t=150 h之间，Ca2+扩散浓度随深度的增加而逐渐减小。当t=150 h，基本达到扩散平衡[38]。因此，下节以t=150 h溶质扩散基本达到平衡时为例，进一步比较分析不同离子浓度和不同离子种类在GCL中的扩散规律。
-
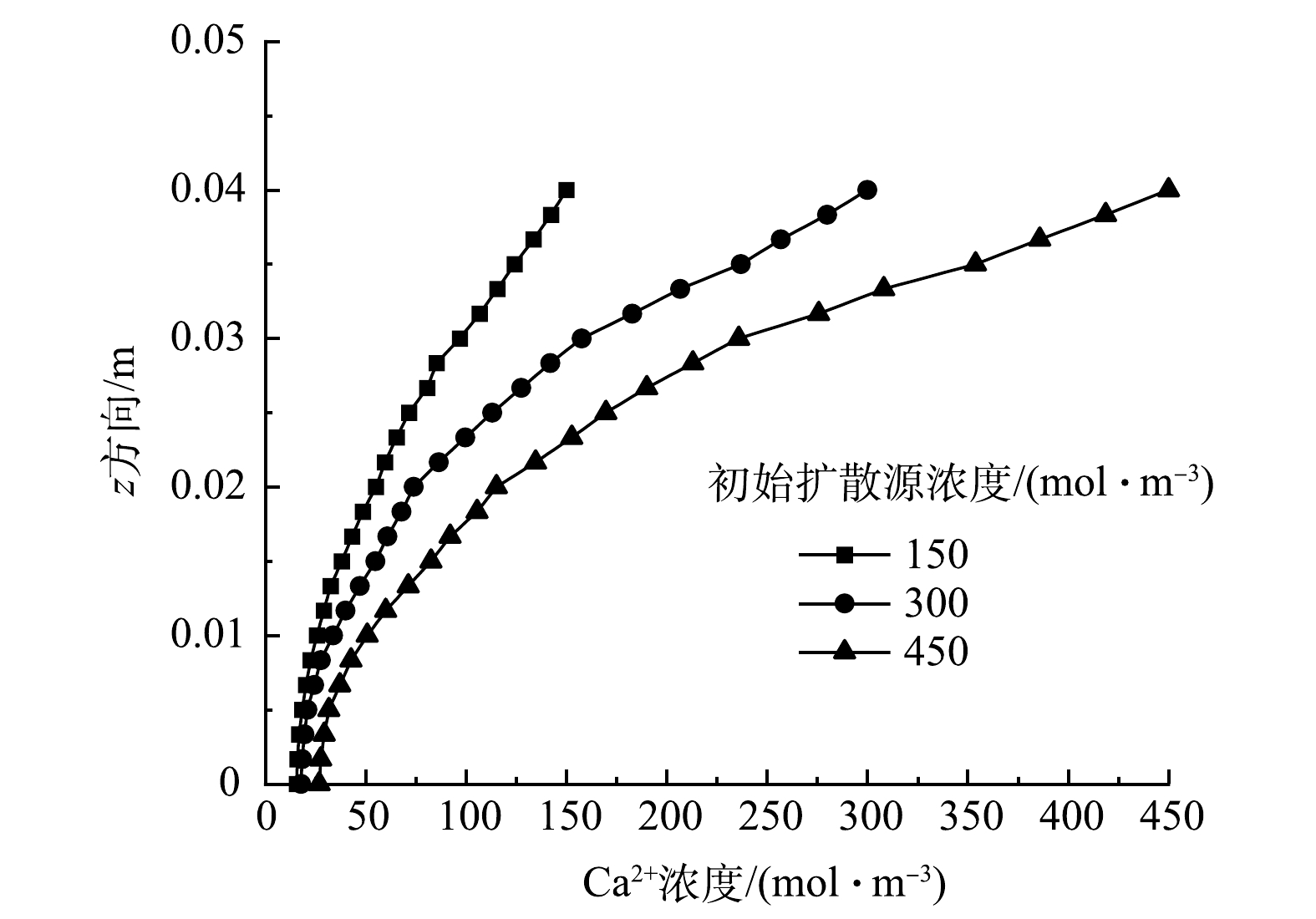
图3给出了t=150 h时，浓度分别为150、300、450 mol∙m−3的Ca2+初始扩散源在z方向的浓度分布图。可以看出，相同竖向位置处，Ca2+扩散浓度随初始扩散源浓度的增加而增大，即溶质的扩散作用随着初始扩散源浓度的增加而增大。进一步比较浓度为150与300 mol∙m−3的Ca2+初始扩散源随深度方向的扩散浓度梯降发现，溶质扩散的梯降随深度增加而逐渐减小。此外，比较初始扩散源浓度为150与300 mol∙m−3、300与450 mol∙m−3的曲线可以看出，初始扩散源处，溶质浓度差均为150 mol∙m−3。但是，溶质扩散后的浓度差与深度呈非线性变化关系。比如，当z=0.03 m时，初始扩散源浓度为150与300 mol∙m−3的浓度差值大于初始扩散源浓度为300和450 mol∙m−3的。但是，当z=0.01 m时，初始扩散源浓度为150与300 mol∙m−3的浓度差值小于初始扩散源浓度为300与450 mol∙m−3的。这说明，溶质在GCL中的扩散，不仅与初始扩散源的浓度有关，而且与扩散距离有关。扩散平衡时，初始扩散源附近，低浓度和中浓度的溶质影响范围较大。但远离初始扩散源处，高浓度初始扩散源的溶质扩散衰减较慢，因此影响范围更大。即低、中和高浓度初始扩散源的影响作用具有相反趋势。因此，当填埋场初始溶质浓度较高时，应尤其对较深范围可能出现的污染进行监测。
-
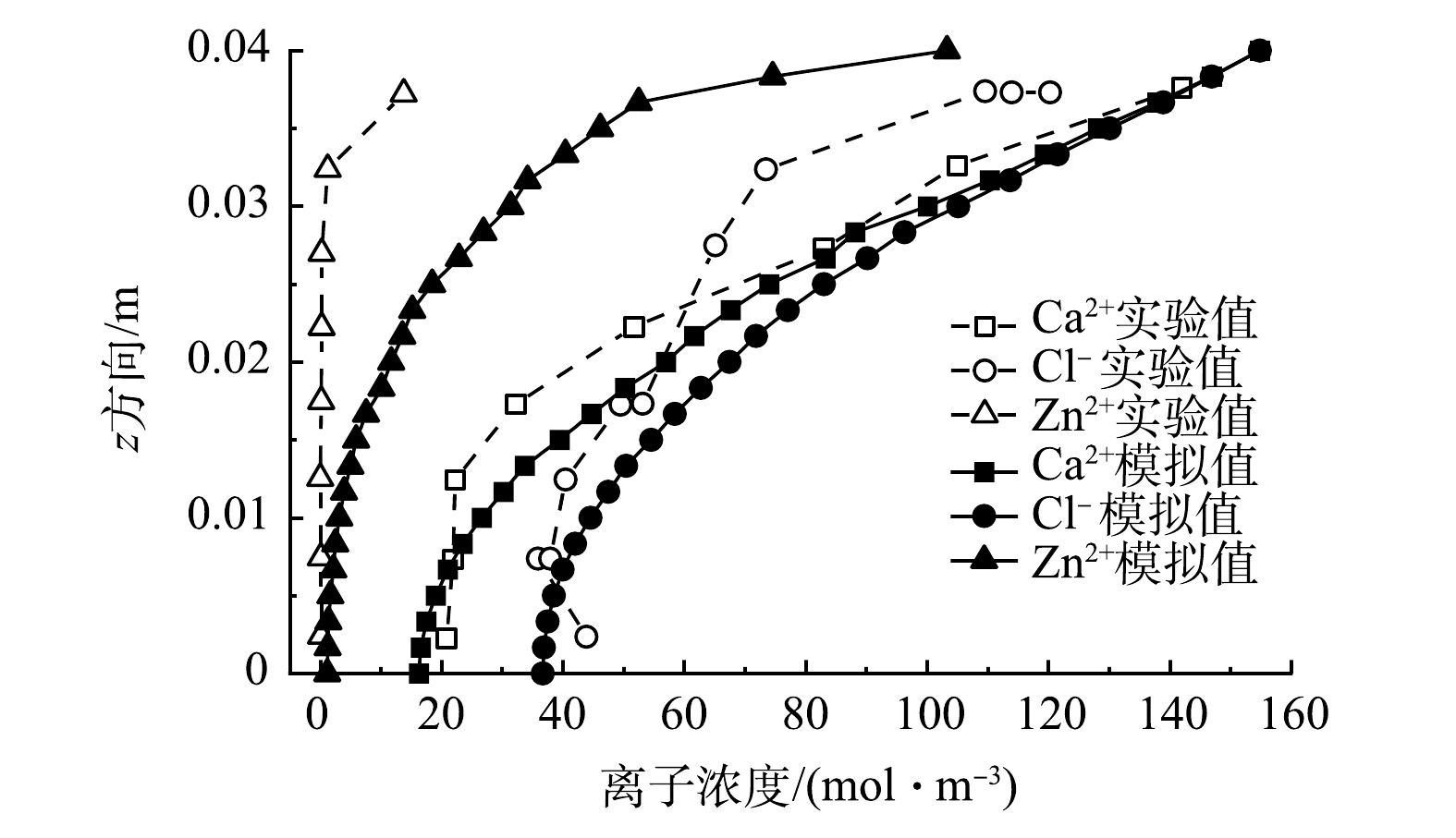
图4给出了t=150 h时扩散场作用下z方向不同种类离子扩散浓度随深度变化的模拟和实验曲线[38]。可以看出，Ca2+、Cl−、Zn2+的模拟值与实验值均表现为离初始扩散源越远(z值越小)离子浓度越小的规律。同时，比较Ca2+与Zn2+阳离子的模拟值发现，扩散系数越大(Ca2+>Zn2+)，离子随深度方向的浓度变化也越大，且随着扩散深度的增加，化学浓度变化逐渐减小。此外，整体Ca2+浓度的变化大于Cl−的，但是，Cl−浓度的差值随扩散深度的增加逐渐增大。这说明，阴离子扩散衰减的速率小于阳离子的。此外可以看出， Zn2+的模拟值较实验值偏大，但Ca2+的模拟值与实验值却非常接近。原因是Zn2+扩散系数远小于Ca2+的，但本研究在COMSOL模拟过程中仅考虑了GCL孔隙率和扩散系数的影响，未考虑膨润土吸湿膨胀及细观孔隙结构的影响。由此可以推测，对于扩散系数较大的阳离子，孔隙率和扩散系数就可以较好地表征其扩散行为。但是，对于扩散系数较小的阳离子，应进一步结合吸湿膨胀及细观孔隙结构演化研究其扩散行为。因此，实际填埋场工程中，应针对不同渗沥液特征，对相应的GCL采取不同安全评估标准。当渗沥液中含大量Ca2+等扩散系数较大的阳离子时，可采取常规测试GCL渗透系数的办法评估GCL的防渗性能。但当渗沥液中含大量Zn2+等扩散系数较小的阳离子时，应进一步加强分析离子在GCL中的运移和扩散特征，才能更准确地评估GCL的防污性能。
-
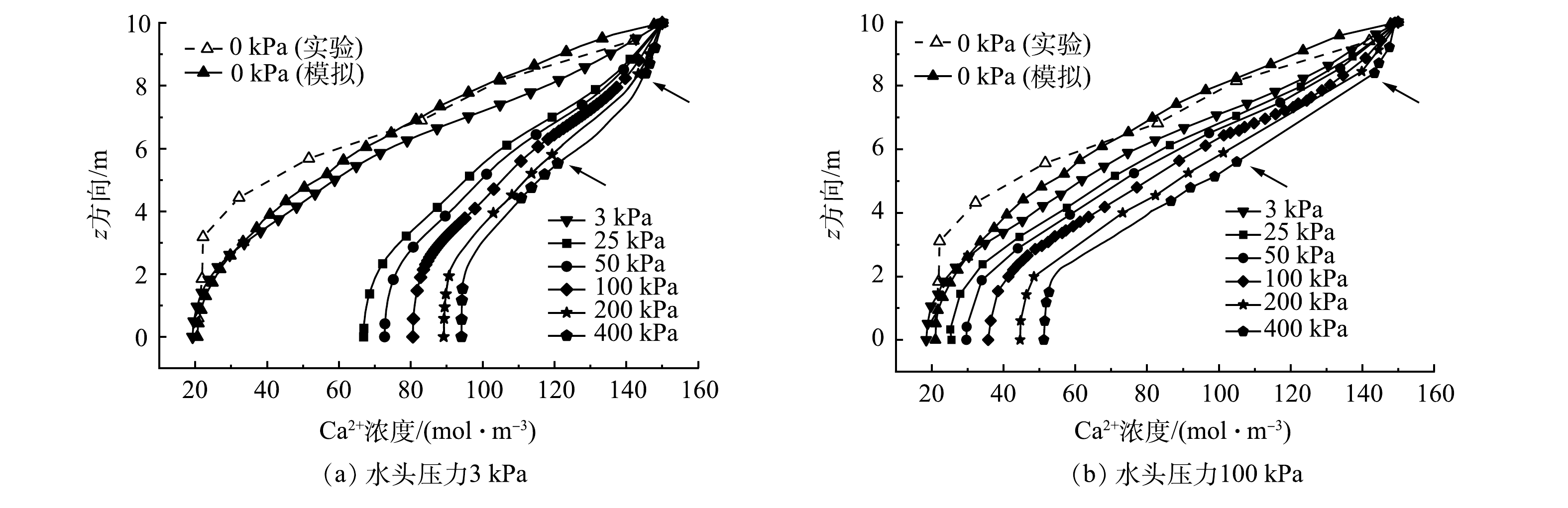
扩散实验较难在水头和上覆应力耦合效应下开展，因此，本研究以Ca2+为例，分别调整模型水头压力为3 和100 kPa，同时施加0、3、25、50、100、200和400 kPa等上覆应力，以研究水头和上覆应力耦合条件下GCL中溶质的扩散规律。
图5(a)所示为水头压力为3 kPa、上覆应力分别为0-400 kPa时，Ca2+浓度在z方向的变化曲线。可以看出，仅在3 kPa水头作用下，Ca2+浓度的模拟值与实验值基本一致。所有上覆应力下Ca2+浓度均随深度增加而呈逐渐减小的趋势，且随着上覆应力的增大，Ca2+扩散浓度随深度的变化逐渐减小。但是，上覆应力大于200 kPa时，Ca2+扩散浓度会在z=8.5和5.5 m位置处出现骤降点，即Ca2+扩散至该深度后，其扩散浓度随深度的增加而急剧减小。此外，值得注意的是，当上覆应力从3 kPa增加至25 kPa时，Ca2+扩散浓度的分布出现较大差异。以远离扩散源z=0 m处为例，当上覆应力分别为3和25 kPa时，该深度处Ca2+扩散浓度分别20和70 mol∙m−3，相差约50 mol∙m−3。而当上覆应力从25 kPa增加至400 kPa时，该处Ca2+扩散浓度仅相差约20 mol∙m−3。这说明，一定水头作用下，一定范围内的上覆应力会在初期较明显地增大GCL中化学溶质的扩散效应，进而促使化学溶质迅速扩散至较深的位置。因此，工程中应尽量避免干燥GCL直接上覆少量垃圾的情况，以防止垃圾填埋初期GCL的防渗性能明显降低。
图5(b)所示为水头压力100 kPa、上覆应力分别为0~400 kPa时，Ca2+浓度在z方向的变化曲线。可以看出，z=0 m时，上覆应力越大，同一深度处的Ca2+扩散浓度越大。上覆应力小于200 kPa时，Ca2+扩散浓度随深度变化比较均匀。而上覆应力大于200 kPa后，与水头压力为3kPa时类似，Ca2+扩散浓度会在z=8.5 m和5.5 m位置处出现骤降点，即Ca2+扩散至该深度后，Ca2+扩散浓度随深度的增加而急剧减小。其原因是，较大的上覆应力使得初始扩散源附近GCL的有效孔隙率明显减小，进而使得其内化学扩散效应显著受限。但随着深度的增加，上覆应力的压密效应逐渐减小，使得化学浓度较大时溶质的扩散效应随渗流明显增大。当z=5.5 m时，尽管上覆应力对有效孔隙率的减小受限，但是由于化学溶质浓度较小，因此GCL中溶质的扩散效应不再明显。继续增加深度后，上覆应力对有效孔隙率的减小几乎可以忽略，有效孔隙率逐渐增大，渗流的作用下，化学扩散再次趋于明显。由此也验证了GCL实验中，溶质的运移在化学和应力作用下存在耦合效应这一现象[35]。
-
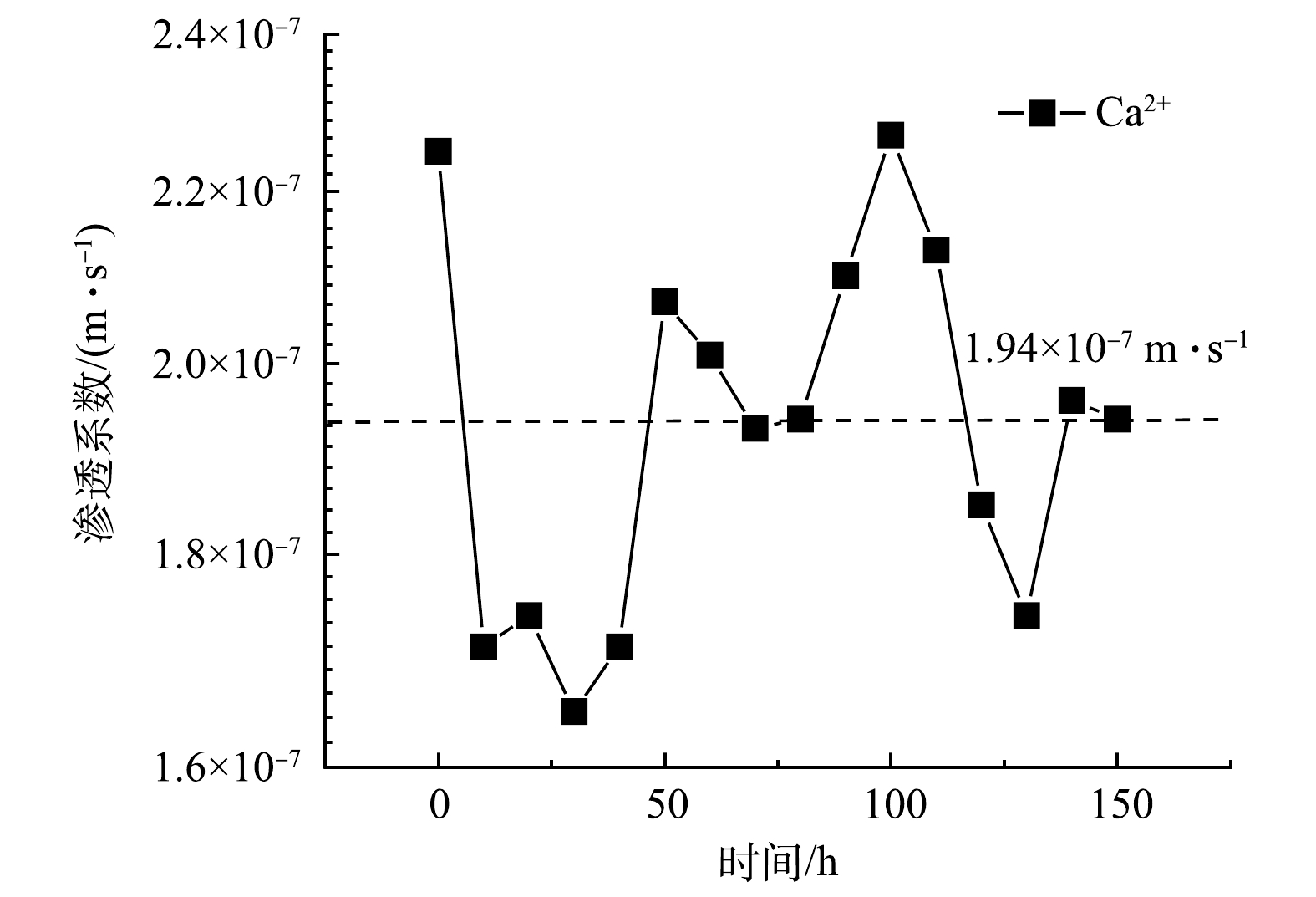
部分学者对膨润土的扩散系数和渗透系数及其相互关系进行了研究[40-42]。图6给出了本模拟Ca2+扩散过程中GCL底部边界渗透系数随时间的变化规律。可以看出，随着Ca2+的扩散，其底部边界处的渗透系数约在1.6×10−7至2.3×10−7 m∙s−1之间，当t=150 h扩散基本平衡时，渗透系数约为1.94×10−7 m∙s−1。
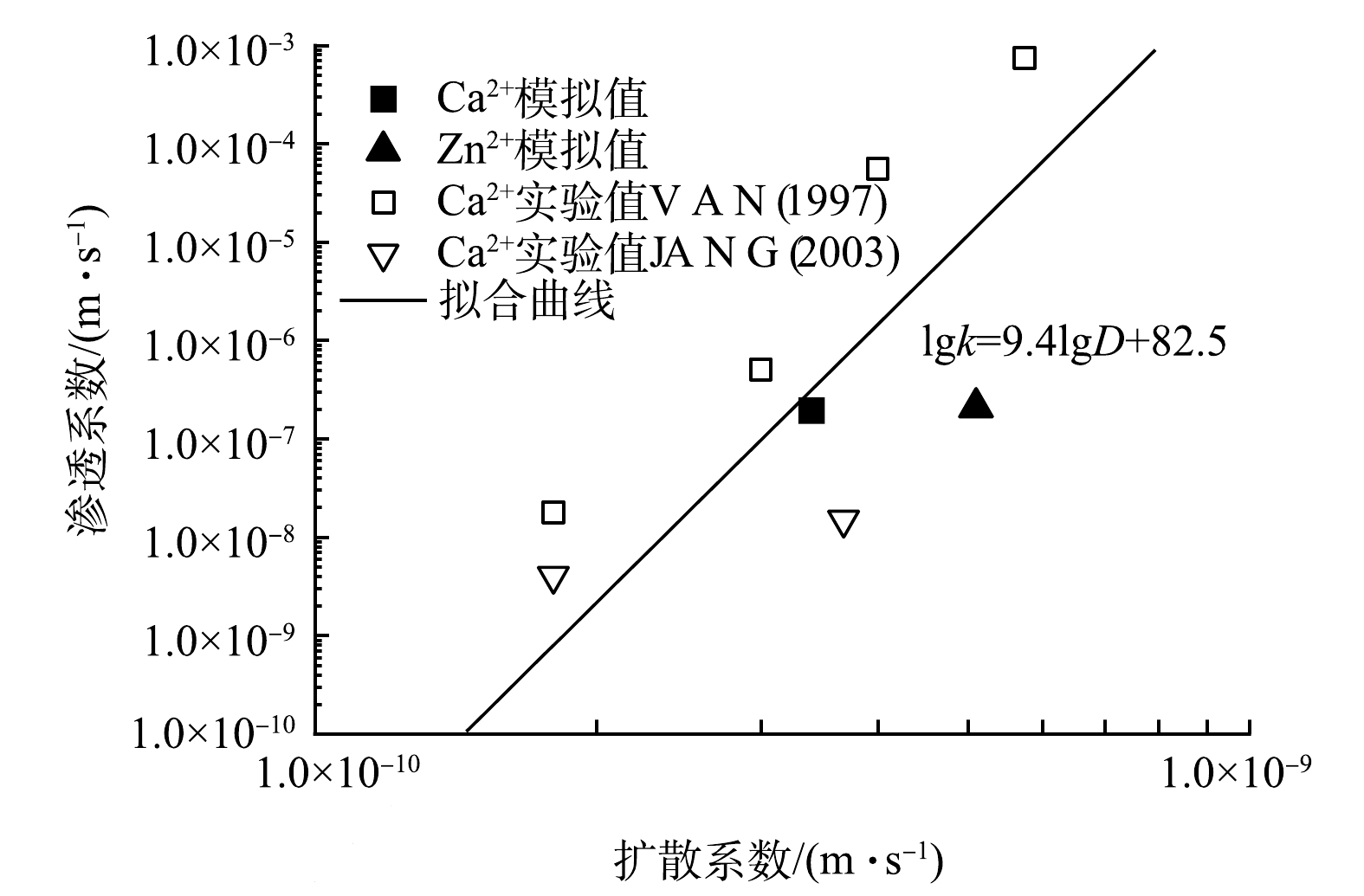
图7给出了本研究所得Ca2+和Zn2+扩散系数与渗透系数之间的模拟关系，同时汇总了JANG等[43]和VAN等[44]的实验值。可以看出，Ca2+的扩散系数和渗透系数值与相同条件下的实验结果非常接近。这说明，本模拟可以较准确地反应溶质在GCL中的扩散行为。同时，由于扩散系数与渗透系数在双对数坐标系下存在一定的线性关系[44-45]，因此，通过拟合模拟和实验数据，可以得到双对数坐标系下渗透系数与扩散系数之间的关系如式(5)所示。
-
1)溶质在GCL中的扩散，不仅与初始扩散源的浓度有关，而且与扩散系数有关。溶质的扩散会加速溶质梯度的变化，扩散速度随时间的增长而逐渐减小，低、中浓度和高浓度初始扩散源的影响作用具有相反的趋势。填埋场工程中当溶质浓度较高时，应尤其注意较深范围内可能出现的污染。
2)扩散系数越大，离子随初始扩散源主扩散方向的浓度变化越大，阴离子比阳离子扩散衰减的速率小。孔隙率和扩散系数可以较好地表征扩散系数较大阳离子的扩散行为，但吸湿膨胀及细观孔隙结构演化等对扩散系数较小阳离子的扩散行为影响不可忽略。
3)化学和应力对溶质在GCL中的扩散存在明显的耦合效应。一定水头作用下，上覆应力会加速GCL中化学溶质向较深位置扩散。填埋场工程中应尽量避免干燥GCL直接上覆少量垃圾的情况，以避免GCL的防渗性能在填埋初期明显降低。
膨润土衬垫溶质扩散及渗透行为COMSOL模拟
COMSOL simulation of solute diffusion and infiltration behavior of geosynthetics clay liner
-
摘要: 针对填埋场膨润土衬垫(GCL)易于被化学溶质击穿的问题，研究了化学溶质在GCL中的扩散行为和破坏机理，以指导工程实际。通过COMSOL Multiphysics构建膨润土扩散柱数值模型，研究了离子种类、离子浓度、水头压力以及上覆应力等因素对化学溶质在GCL中扩散行为的影响，并研究了渗透系数与扩散系数之间的转换关系。结果表明，阴离子比阳离子的扩散衰减速率小，扩散速率随溶质扩散时间的增长而减小，化学溶质的扩散会显著增加溶质浓度梯度的变化。对于扩散系数较大的溶质，孔隙率和扩散系数能较好地表征其扩散行为。上覆压力会明显增大化学溶质在GCL中的扩散。低、中浓度初始扩散源的扩散范围较浅，而高浓度初始扩散源的扩散范围较大。因此，在垃圾填埋场工程中，应根据渗沥液浓度、离子种类以及上覆垃圾荷载等对GCL的防污性能进行安全评估，尤其应对高浓度和高应力作用下较深范围内污染物的迁移情况进行监测。本研究结果可为GCL在填埋场中的工程应用和防污安全预警提供参考。
-
关键词:
- 膨润土衬垫 /
- 扩散行为 /
- 渗透系数 /
- COMSOL多物理场模拟
Abstract: Regarding to the chemical break-down of the geosynthetics clay liner (GCL) in landfill, the diffusion behavior and the failure mechanism was numerically studied to guide engineering practice. A serious of COMSOL Multiphysics numerical model was developed based on the diffusion column tests. The effects of chemical ionic species and concentrations, the water gradient and the overlying pressure on the diffusion behavior of the GCL were investigated. A relationship between the hydraulic conductivity and diffusion coefficient was exploded. The results demonstrated that the decays rate of anion diffusion was lower than that of cations. The diffusion rate was gradually decreased with the time. The chemical diffusion accelerated the change of the solution gradient. The porosity and diffusion coefficient can screen well the diffusion behavior of the GCL with larger diffusion coefficients. Under a certain water gradient, the overlying pressure increased the chemical diffusion through the GCL at the initial stage, and moved to a deeper position. The low and medium concentrations influenced the area nearby the initial diffusion source. However, the initial diffusion source with high concentration influenced a larger area. Therefore, the chemical diffusion and hydraulic performance of GCL in a landfill project should be evaluated carefully according to the concentration of leachate, the type of chemical ions, and the overlying pressure. The migration of pollutants should be monitored, especially relating to the high chemical concentration and high-pressure condition. The research results provided a theoretical reference for the application of GCL in landfills, as well as the risk assessment and early warning systems.-
Key words:
- GCL /
- diffusion behavior /
- the hydraulic conductivity /
- COMSOL multiphysics simulation
-
我国城市给水厂每年所产生的污泥约为1.5×108 m3[1]，其中含有大量的有机物、重金属以及致病菌和病原菌等，若不加处理任意排放，将成为危险的二次污染源，通过大气、地下水、地表水和土壤等介质进入食物链，造成严重的生态风险，影响人类健康[2]。作为给水厂的伴生产物，目前城市给水厂污泥有效资源转化率不足10%，且大多数采用卫生填埋、焚烧、土地利用[3]和投海等传统方法处理污泥，既不能有效利用可再用资源又容易造成二次污染。给水厂污泥中不仅含有大量的铁盐、铝盐混凝剂成分外，还含有活性炭组分[4]，将给水厂污泥制成颗粒状吸附剂用于吸附除磷，不仅可以降低给水厂污泥处置费用，同时污水除磷成本也大大低于化学除磷。并且给水厂污泥吸附除磷不会增加污泥量，不容易受出水SS，原水水质，脱氮条件等影响，去除率远高于传统生物除磷法。采用给水厂污泥来吸附污水中的磷，变废为宝，还可以达到资源化利用的目的。
有关给水厂污泥吸附除磷的研究工作多采用静态吸附搅拌的方法[5-8]，该方法用于实验室的实验研究是行之有效的，但难以在实际生产中推广使用。本研究采用北京市某给水厂废弃污泥为原材料，制备成颗粒状吸附剂用于连续处理初沉池水的动态吸附实验方法，为给水厂污泥用于实际生产中提供了一定理论和实验基础。
1. 材料与方法
1.1 仪器与试剂
试剂：磷酸二氢钾、抗坏血酸、钼酸铵、酒石酸锑氧钾、浓硫酸、氢氧化钠，均为分析纯，购自国药集团化学试剂有限公司。废弃铁铝泥取自北京市某大型给水厂，对该自来水厂的混凝剂投加种类和投加量等数据进行收集分析，该厂每天投加铝盐和铁盐2种混凝剂。本实验所用水均为北京某城市污水处理厂初沉池出水。
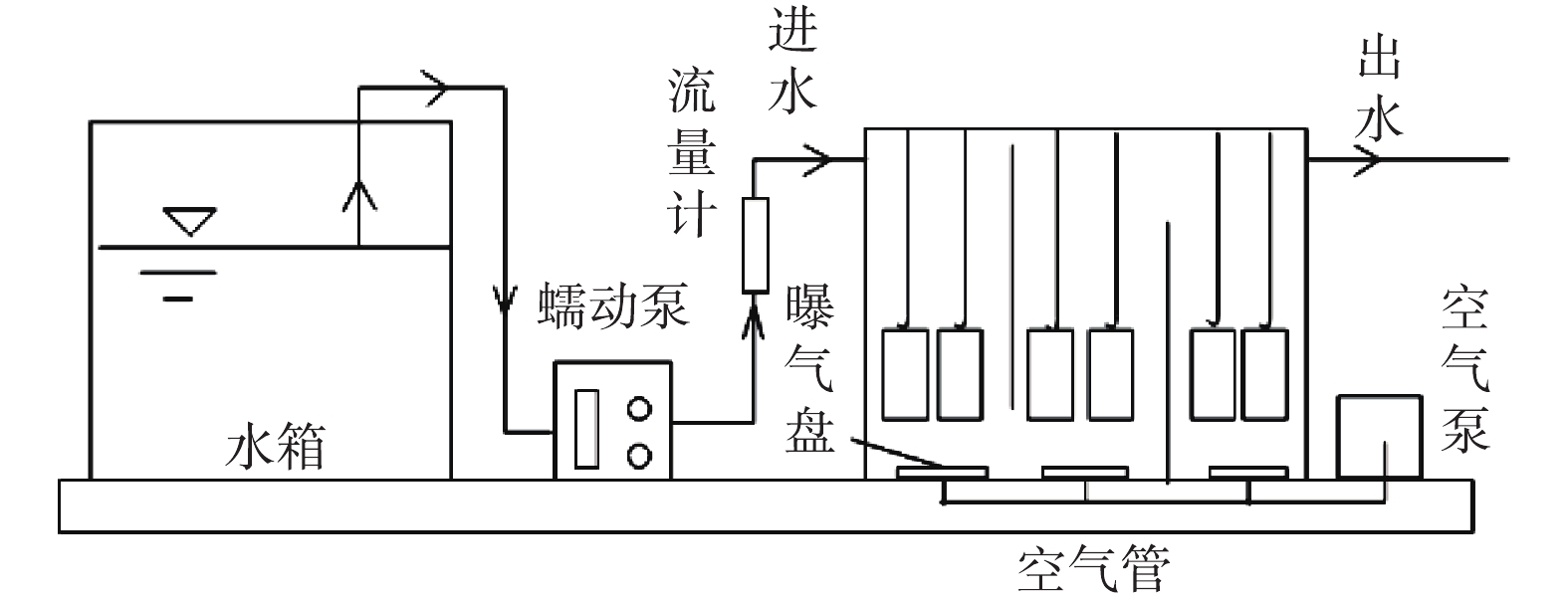
仪器：紫外可见分光光度计、六联混凝搅拌器、恒温搅拌器、硬度测定仪等。动态吸附实验装置详见图1和图2。2 mm动态吸附实验吸附装置如图1所示，长为0.94 m、宽为0.75 m、高为0.76 m，装置底部装有的曝气盘可以向装置内部曝气使得装置内部污水与2 mm颗粒吸附剂充分混合接触。污泥颗粒装入金属网袋中并用金属网钩均匀悬挂在装置内。小型固定床吸附柱装置如图2所示。柱身内径为4 cm，吸附剂装填高度为14.2 cm，采用上向流。
1.2 材料的制备
铁铝泥样品取回后放置于室外平铺晾晒，使得污泥含水率由83%降至67%左右(污泥外表成团状)。一部分污泥用铁铲经人工碾碎后放入摇摆式造粒机中通过3 mm的孔径磨具挤出，置于室外自然风干，制成低硬度的粒径约为2 mm的小颗粒。另一部分污泥放入干化机中挤压造粒后在干化机内部65 ℃干化1.5 h，成为含水率50%的大污泥颗粒，后再置于室外自然风干，制成尺寸为长约为12 mm、直径约为7 mm的柱状高硬度干化大颗粒。
1.3 给水厂颗粒污泥的表征
废弃铁铝泥中元素分析采用X射线荧光光谱分析法(XRF)，检测依据是JY/T016-1996波长色散型X射线荧光光谱法通则，仪器名称为X射线荧光光谱仪ZSX PrimusII。外表形貌的测定采用型号为S-3400N的扫描电子显微镜，将少量颗粒涂在导电胶上，固定在样品台上进行观察；采用ASAP2420比表面积及孔径分析仪，利用高纯氮气吸附介质测定吸附脱附等温线，采用BET法计算比表面积，采用t-plot计算微孔比表面积和微孔体积，总孔吸附平均直径根据总孔体积和比表面积计算得出；将制备的2种颗粒分别在去离子水中浸泡72 h后，先测定2种颗粒的脱落率，再用硬度测定仪分别检测浸泡前后2种颗粒的硬度。
1.4 吸附实验
向2个1 L烧杯中各加入1 L初沉池水，再分别加入10 g 2种不同粒径的颗粒，使用六联搅拌器以120 r·min−1的速度搅拌8 h，间隔2 h取一次水样，测定反应体系中各种形态的磷含量。分别考察了2 mm颗粒吸附剂和干化大颗粒吸附剂对初沉池污水中磷动态吸附的影响因素。
1)吸附剂投加量对出水磷浓度的影响。控制2 mm颗粒吸附剂投加量为10 g·L−1和20 g·L−1，将2 mm颗粒装入金属网袋中，并用金属网钩均匀悬挂在装置内，控制进水流量45 L·h−1，污水中空气曝气量7.2 m3·h−1，先开启进水泵，当装置满水并且有出水后将装有2 mm颗粒吸附剂的金属网带悬挂放置于反应器内，同时开始计时。反应8 h每间隔2 h在出水口处取样测定出水中各种形态磷的含量。
2)吸附时间对出水磷浓度的影响。控制2 mm颗粒吸附剂投加量为20 g·L−1，将2 mm颗粒装入金属网袋中并用金属网钩均匀悬挂在装置内，控制进水流量为45 L·h−1，污水中空气曝气量为7.2 m3·h−1，先开启进水泵，当装置满水并且有出水后将装有2 mm颗粒吸附剂的金属网带悬挂放置于反应器内，同时开始计时，反应时间为56 h，每间隔一段时间在出水口处取样测定出水中各种形态磷的含量。
3)空床停留时间(EBCT)对出水磷浓度的影响。控制干化大颗粒滤柱的空床停留时间分别为5、10、20、30 min。分别测出不同停留时间下出水水中各种形态磷的含量。
4)滤层高度对出水磷浓度的影响。控制干化大颗粒滤柱的空床停留时间为30 min，分别在不同滤层高度处(2.3、4.7、7.1、9.5、11.8、14.2 cm)检测出水水中各种形态磷的含量。
5)吸附时间对出水磷浓度的影响。控制干化大颗粒滤柱的空床停留时间为30 min，滤层高度为14.2 cm。连续运行135 h，每间隔一段时间在出水口处取样测定出水中各种形态磷的含量。
1.5 分析方法
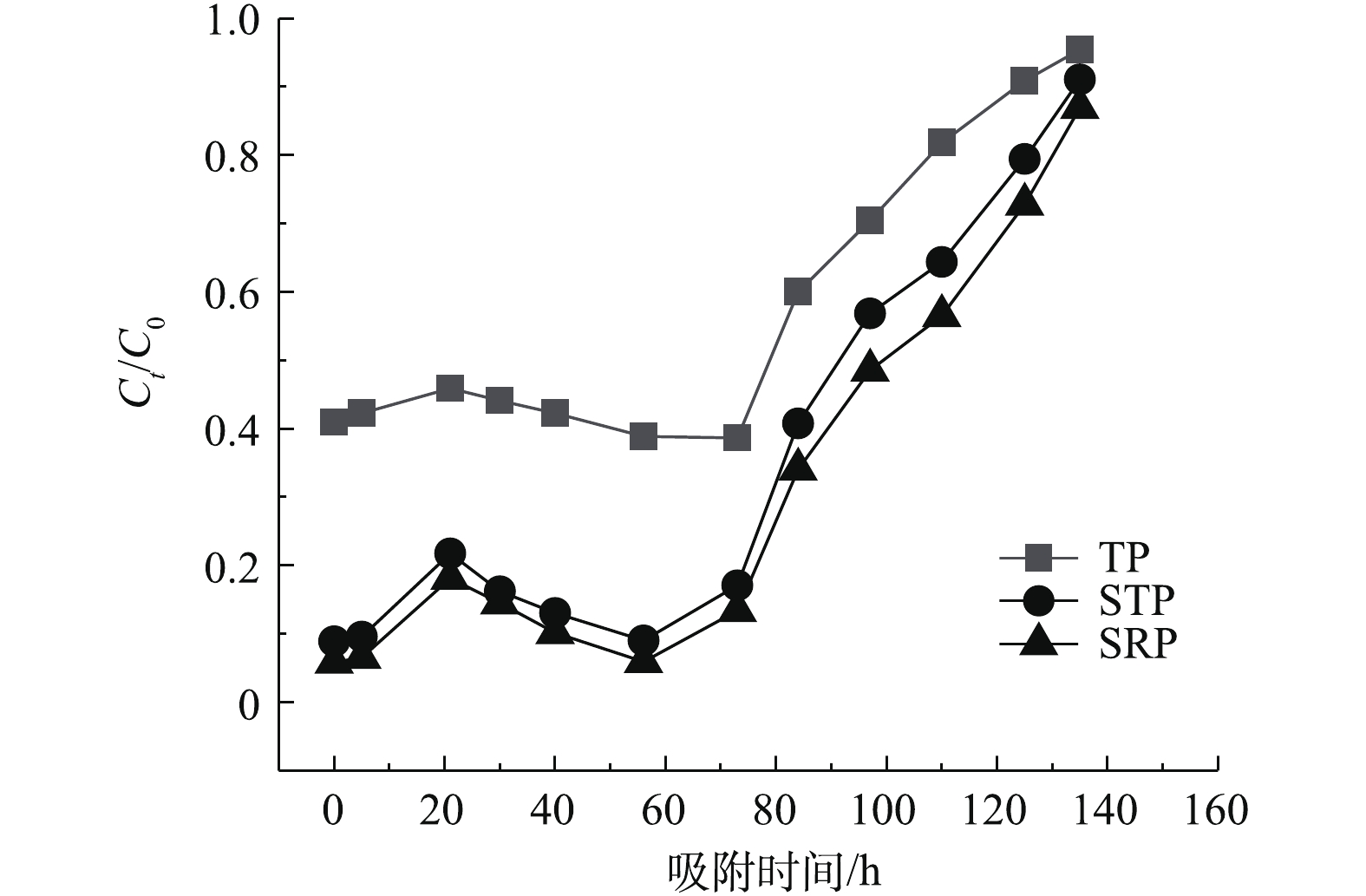
磷的测定采用钼锑抗分光光度法，根据不同的预处理方法将磷的形态分为总磷(total phosphorus，TP)、可溶性总磷(soluble total phosphorus，STP)、可溶性活性磷酸盐(soluble reactive phosphorus，SRP)、颗粒态磷(particulate phosphorus，PP)及其他溶解磷[9]。原水样直接消解测得TP含量；经0.45 μm滤膜过滤，消解测得STP含量；经0.45 μm滤膜过滤但不消解测得SRP含量；TP减去STP得PP；STP减去SRP得出其他溶解磷含量。
2. 结果与讨论
2.1 2种颗粒污泥的表征
废弃铁铝泥粉末XRF检测结果见表1。由表1可知，污泥粉末主要含有C、O、Al、Fe、Si、Ca等元素，质量分数分别为10.5%、51.9%、6.74%、15.9%、8.81%，主要物质应为SiO2、Al2O3、Fe2O3和CaO。检测结果与SONG等[10]的检测结果一致。由表1可知，废弃铁铝泥的性质与黏土性质相似，且该水厂Fe盐混凝剂投量高于Al盐混凝剂投量。
表 1 废弃铁铝泥粉末的组分分析结果Table 1. Composition analysis of waste Iron and aluminum sludge powder元素 质量分数/% 元素 质量分数/% 元素 质量分数/% C 10.5 Cl 0.29 Zn 0.007 4 O 51.9 K 0.451 As 0.009 8 Na 0.173 Ca 2.78 Br 0.004 1 Mg 0.434 Mn 0.128 Rb 0.002 8 Al 6.74 Ti 0.117 Sr 0.011 1 Fe 15.9 V 0.017 2 Zr 0.005 1 Si 8.81 Cr 0.009 6 Mo — N 1.26 Co — Pb — P 0.069 1 Ni 0.004 Ba 0.023 2 S 0.323 Cu 0.004 U — | Show Table
DownLoad:
CSV
图3、图4和表2分别为2种颗粒的表面形貌、比表面积和孔隙结构表征结果。图3(a)和图3(b)分别为2 mm小颗粒和干化大颗粒外观图。对比图4(a)和图4(b)可知，2种颗粒孔隙结构均较发达。由表1可知，干化大颗粒与2 mm小颗粒相比，比表面积和微孔体积分别减少了46.2%和33.6%，比表面积的降低是由于2种颗粒粒径相差较大，干化大颗粒比表面积远小于2 mm颗粒。微孔体积的减小推测可能是由于摇摆式造粒和干化机挤压造粒2种不同的造粒方式所致。由表1可知，干化大颗粒的优点在于具有较高的硬度，并且脱落率较低。2 mm颗粒在25 ℃、pH为7时的吸附容量为12.39 mg·g−1，高于干化大颗粒。综合考虑2种污泥颗粒的各项性能，将2 mm颗粒装入金属网袋中，且悬挂在图1所示装置内，再进行连续流动态吸附实验。金属网袋可以有效减少因水流冲刷作用造成的颗粒损失，并且当颗粒吸附达到饱和时方便及时更换。2 mm颗粒由于粒径过小且硬度同样较小，应用在滤柱装置内作为滤料可能会出现滤柱堵塞的情况发生，干化大颗粒粒径较大，硬度和脱落率较低可有效降低滤柱堵塞的情况，因此，采用干化大颗粒作为滤柱滤料进行动态吸附除磷实验。
图 4 2 mm颗粒和干化大颗粒SEM图片Figure 4. SEM images of 2 mm particles and dried large particles表 2 2种不同硬度颗粒的性能比较Table 2. Comparison of performance of particles with two different hardness吸附剂 尺寸/mm 硬度/N 脱落率/% 比表面积/(m2·g−1) T图法微孔体积/(cm3·g−1) 总孔吸附平均直径/nm 理论吸附量/(mg·g−1) 干化大颗粒 L=12D=7 30.31 10 68.53 0.008 9 4.08 5.24 2 mm D=2 24.70 16 127.29 0.013 4 4.12 12.39 | Show TableDownLoad:
CSV
2.2 某污水处理厂初沉池水中磷浓度及形态表征
对北京市某污水处理厂的初沉池污水中磷的形态分布及浓度水平进行了分析，采集不同时段的初沉池污水进行不同形态磷的测定分析，结果如下：该厂初沉池出水中总磷浓度在4.0~6.8 mg·L−1；可溶性总磷浓度在3.1~5.4 mg·L−1；可溶性活性磷酸盐浓度在2.4~3.1 mg·L−1；可溶性非活性磷酸盐浓度在0.7~2.7 mg·L−1，颗粒态磷浓度在0.9~2.0 mg·L−1。各种形态磷含量的分布规律为可溶性总磷>可溶性活性磷酸盐>颗粒态磷>可溶性非活性磷酸盐。由于可溶性总磷和可溶性活性磷酸盐在初沉池出水中占据较大比重，因此，本研究将对于可溶性总磷和可溶性活性磷酸盐去除率作为衡量初沉池出水中磷去除效果优劣的标准。
2.3 给水厂颗粒污泥的对初沉池污水中磷的静态吸附
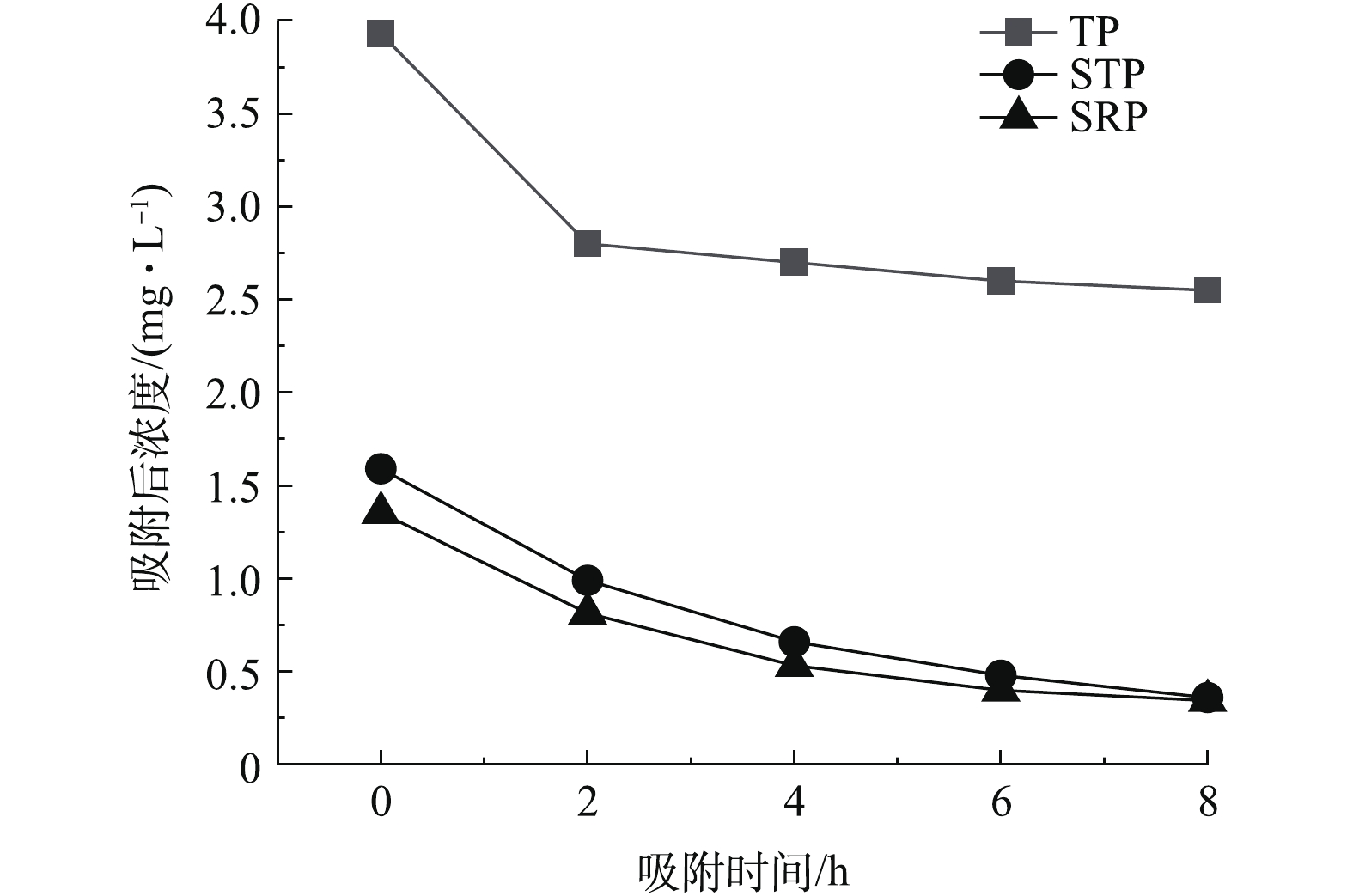
图5和图6分别为2种污泥颗粒对于初沉池中不同形态磷的去除效果。在前2 h内，污泥颗粒的对水中各种形态磷的去除效率较高，8 h左右基本达到吸附平衡。通过对2种污泥颗粒对水中各种形态磷的吸附效果比较，可以看出，污泥颗粒对于水中溶解态活性磷的去除效果较好，这是由于污泥颗粒对于水中磷的吸附以化学吸附为主，其主要吸附机理是依靠污泥颗粒表面的羟基、硫酸根与磷酸盐的配位交换或者形成铝的羟基磷酸盐络合物[11]。对于水中颗粒态的磷，主要依靠污泥颗粒的孔隙截留作用去除，由于2 mm颗粒比表面积大于干化大颗粒，因此，在吸附8 h后2 mm颗粒出水的总磷浓度为1.45 mg·L−1，小于干化大颗粒出水总磷浓度。同时，由图5和图6可知，反应8 h后2 mm颗粒出水总磷 、STP、SRP的浓度分别为1.45、0.11、0.036 mg·L−1；干化大颗粒出水TP 、STP、SRP的浓度分别为2.55、0.36、0.34 mg·L−1，2 mm颗粒比表面积和理论吸附容量均高于干化大颗粒，因此，在初沉池水中对磷的去除效果优于干化大颗粒。
图 6 干化大颗粒对磷的静态吸附曲线Figure 6. Static adsorption curve of dried large particles to phosphorus2.4 2 mm颗粒吸附剂对初沉池污水中磷的动态吸附
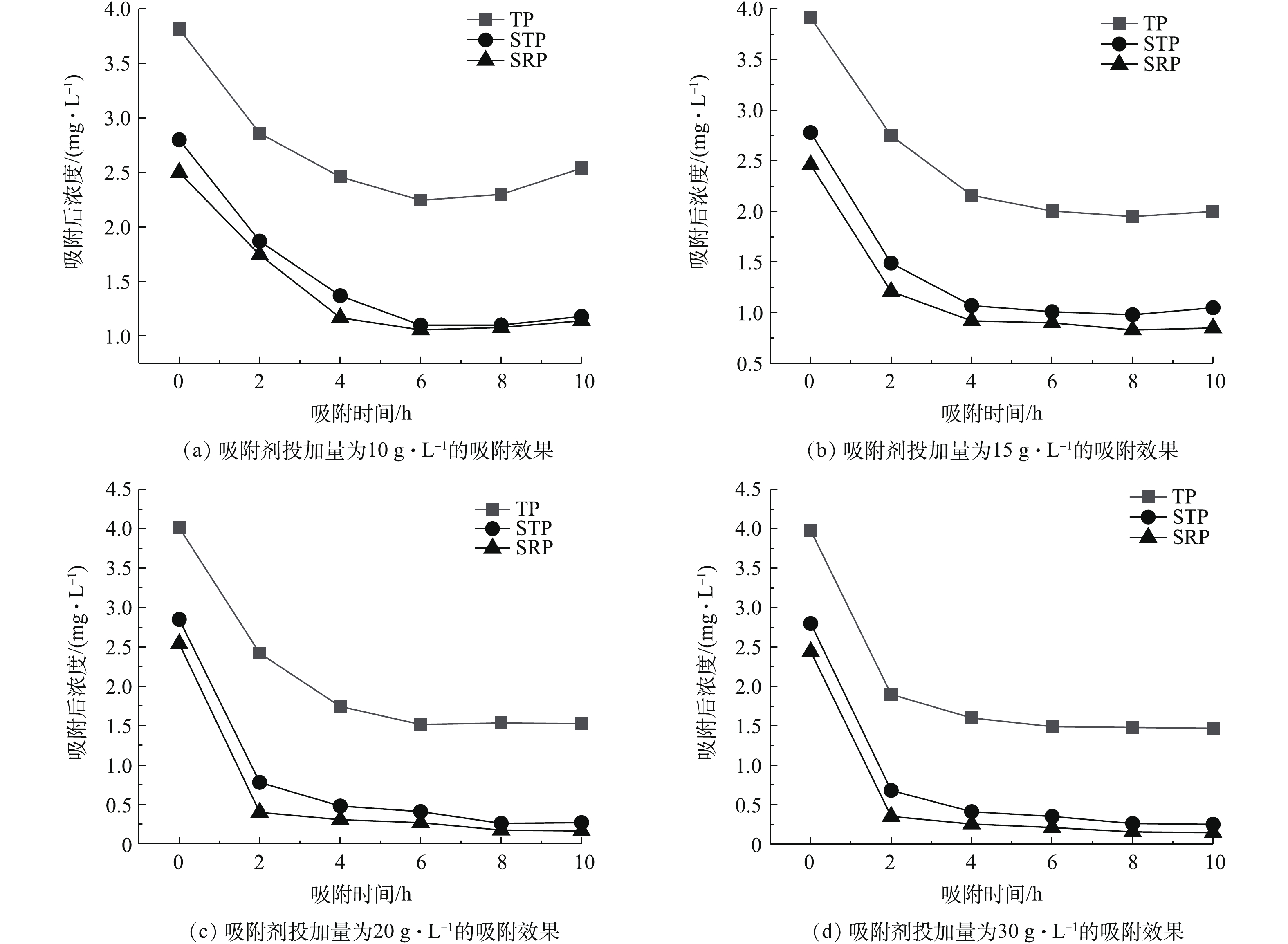
1)不同颗粒投加量下2 mm污泥颗粒在连续流中去除对比效果见图7。由10 g·L−1投量的静态吸附和动态吸附效果对比(图5和图7(a))可以看出，连续流吸附时出水磷的吸附效果远低于静态吸附实验，在吸附8 h后，出水TP浓度为2.3 mg·L−1、STP和SRP浓度分别为1.1 mg·L−1和1.07 mg·L−1。增加吸附剂投加量至15 g·L−1时吸附效果增加幅度有限。当颗粒投量为20 g·L−1时，吸附效果明显提高，出水TP浓度为1.52 mg·L−1，STP和SRP浓度分别为0.27 mg·L−1和0.16 mg·L−1。考虑到继续增加投加量至30 g·L吸附效果并未显著增加反而会增加较多成本，故认为20 g·L−1为最适宜投加量。
图 7 吸附剂投加量对出水磷浓度的影响Figure 7. Effect of adsorbent dosage on effluent phosphorus concentration2) 2 mm颗粒动态吸附实验中时间对出水磷浓度的影响结果如图8所示。在吸附初始阶段，由于颗粒表面空余活性吸附位点较多并且污泥颗粒表面与污水界面处具有较大的磷浓度梯度，传质推动力较大，有利于污泥颗粒对于溶液中磷的吸附，因此，污水中磷浓度快速降低。在吸附2 h后污泥颗粒表面与污水界面处磷浓度梯度逐渐减小，出水磷去除率升高缓慢，8 h后出水磷去除率达到最大。在运行后期，反应器深度除磷持续运行效果降低。
图 8 2 mm颗粒对磷的动态吸附曲线Figure 8. Dynamic adsorption curve of 2 mm particles to phosphorus2.5 干化大颗粒对初沉池污水中磷的动态吸附
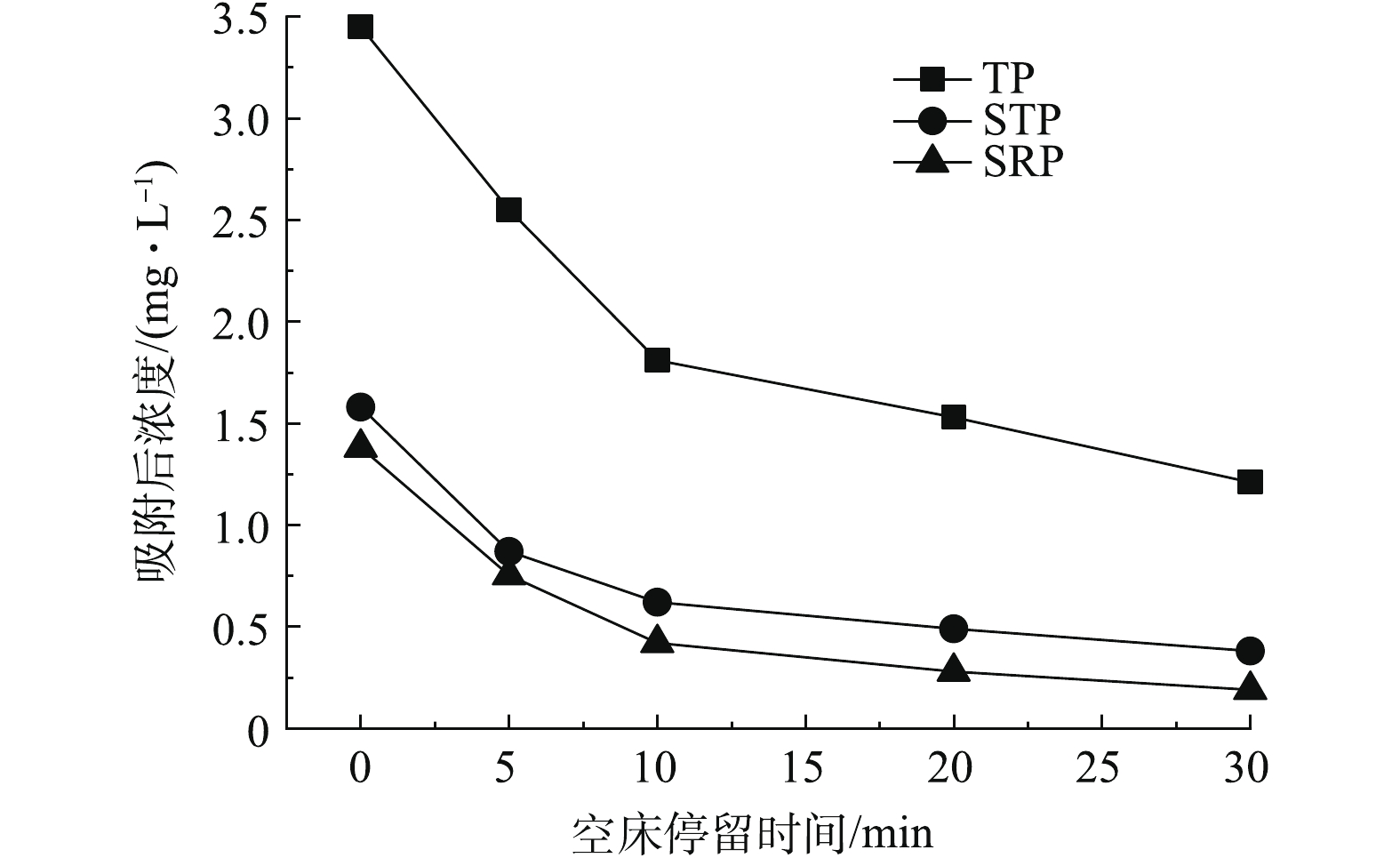
1)空床接触时间对各种形态磷去除率的影响结果见图9。由图9可知，总磷含量的降低大部分归功于溶解态活性磷酸盐含量的降低。颗粒态磷和其他溶解态磷含量虽然也有一定程度的降低，但幅度很小。这说明污泥颗粒主要依靠化学吸附去除水中溶解态磷，而对于颗粒态磷则依靠物理截留作用，去除效果一般。随着EBCT的增加，总磷、溶解性总磷以及可溶性活性磷酸盐的去除率均大幅度增加，这是由于EBCT较小，上柱滤速过大，一部分磷还没来得及被干化大颗粒吸附便流出滤柱。当EBCT为30 min时，各种形态的磷去除率虽有提高，但并不显著。虽然继续增大EBCT对吸附有利,但EBCT过大会会降低处理效率，从时间上增加能耗成本,所以干化大颗粒滤柱的空床停留时间应控制在30 min左右。
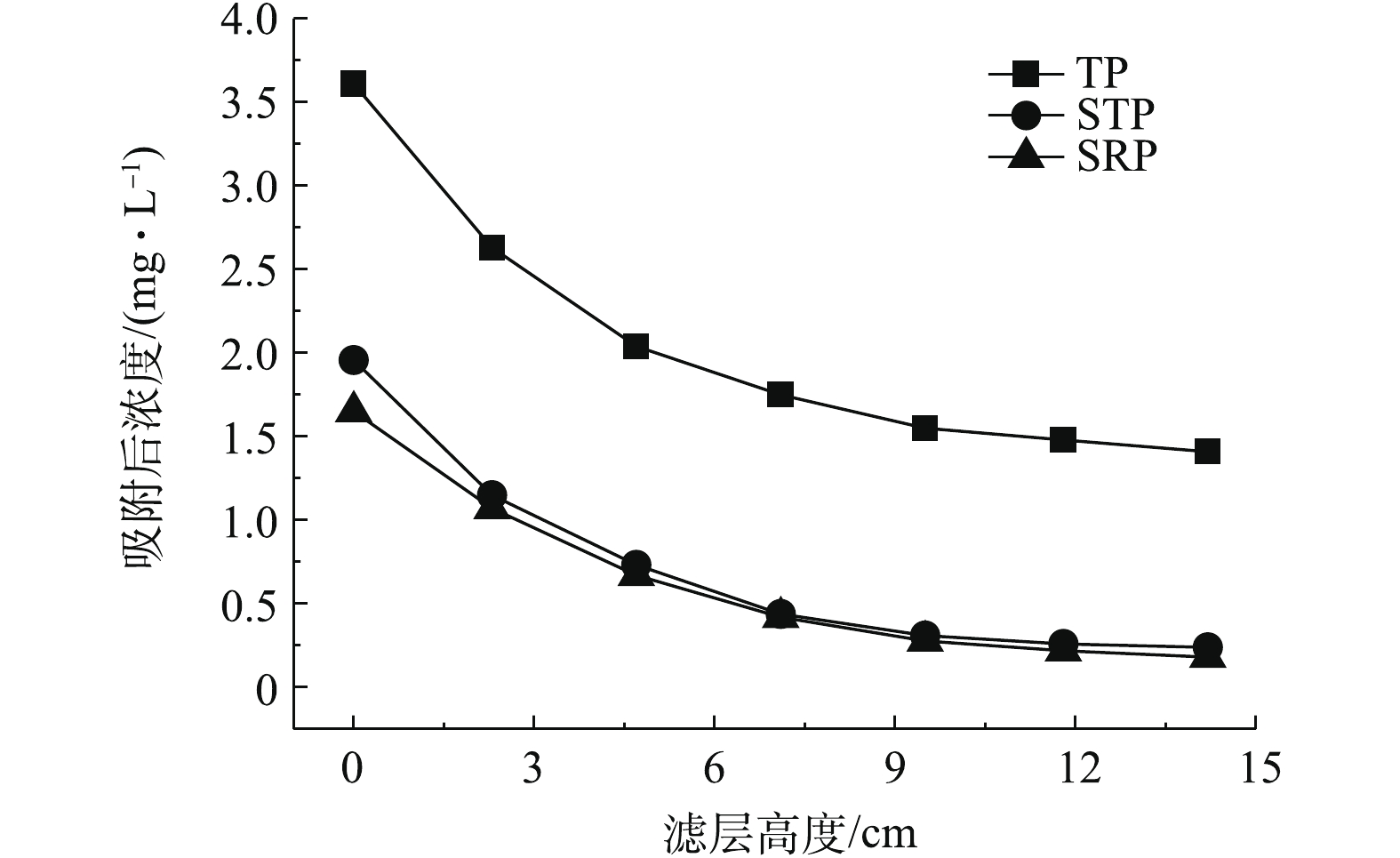
图 9 EBCT对干化大颗粒出水不同形态磷浓度的影响Figure 9. Effect of EBCT on effluent concentration of different phosphorus forms after dried large particles adsorption2)不同滤层高度对出水磷浓度的影响结果见图10。由图10可知，随着滤层高度的增加，出水总磷，可溶性总磷和可溶性活性磷酸盐的浓度均大幅度降低。当滤柱的滤层高度在11.5 cm和14.2 cm时，出水中不同形态的磷浓度并无显著降低，故可确认11.5 cm为干化大颗粒滤柱的有效滤层高度。
图 10 干化大颗粒不同滤层高度对磷去除率的影响Figure 10. Effect of different filler heights of dried large particles on phosphorus removal rate3)为考察干化大颗粒的吸附时间对实际废水的动态处理效果影响，以运行时间为横坐标，Ct/C0为纵坐标绘制穿透曲线，处理结果如图11所示。以出水浓度为进水浓度的10%为穿透点，反应器穿透时间为5 h；以出水浓度为进水浓度的90%为反应终点，反应器运行至135 h后，认为达到饱和。由图11可知，反应器对于TP的吸附效果较差，这是因为初沉池水中的组分较为复杂，悬浮物质、有机质等等均会引入污染吸附剂，对吸附效果造成一定影响。但从STP和SRP的处理效果来看，在固定床反应器的运行前期(0~80 h)，干化大颗粒依然对实际废水有良好的处理效果。但后续水体中其他物质的影响对磷的去除影响较大，导致固定床反应器吸附除磷持续运行效果降低。
图 11 干化大颗粒连续流动态吸附实验Figure 11. Continuous flow dynamic adsorption test of dried large particles2.6 技术经济分析
现依托污水处理厂为工程技术经济分析背景，以废弃铁铝泥颗粒状吸附剂生产成本为主要考虑对象，对颗粒吸附剂制备进行技术经济估算分析。利用给水厂废弃铁铝泥颗粒吸附除磷，对于STP浓度为2.85 mg·L−1的原水，按深度除磷后出水STP浓度低于0.26 mg·L−1计算，理论上处理初沉池水所需药剂费用为0.021 2元·t−1，低于化学沉淀法除磷的药剂费用。对于铁铝泥颗粒状吸附剂，虽然其无法达到深度除磷要求，但具有较低的使用成本，可以用于污水厂前端工艺中，可有效降低水厂后续工艺中絮凝剂的投加量，从而减少水厂的运行成本。此外，还可以同时降低给水厂废弃污泥的后续处置处理费用，从而达到污泥资源化利用的目的。
3. 结论
1)给水处理厂废弃铁铝泥主要含有碳、氧、铝、铁、硅等元素，孔隙发达，具有较大的比表面积，适宜吸附水中的磷。
2)给水厂污泥制成的2种粒径颗粒作为吸附剂对初沉池水中磷进行静态吸附，2 mm粒径颗粒由于具有较大的比表面积，故吸附效果优于干化大颗粒。
3) 2 mm颗粒的动态吸附实验结果表明，其适宜投加量为20 g·L−1，实验初始阶段，水中磷浓度快速降低，连续运行8 h后达到最佳去除效果。
4)干化大颗粒的动态吸附实验结果表明，滤柱的空床停留时间应控制为30 min、滤层有效高度为11.5 cm。反应器穿透时间为5 h，反应器运行至135 h后，认为达到饱和。在固定床反应器的运行前80 h，干化大颗粒对初沉池水有良好的处理效果。
5)经济分析表明，颗粒吸附剂理论上处理初沉池水所需药剂费用为0.021 2 元·t−1，具有较高的经济效益。
-
图 2 不同时刻Ca2+扩散浓度分布图
Figure 2. Diffusion concentration distribution of Ca2+ at different times
图 3 具有不同初始扩散源浓度的溶质随深度扩散变化图（CaCl2）
Figure 3. Solutions with different initial diffusion source concentrations vs the depth (CaCl2)
图 4 不同种类离子扩散浓度随深度变化曲线(Ca2+、Cl−、Zn2+)
Figure 4. Diffusion concentrations of vary ions vs the depth (Ca2+、Cl−、Zn2+)
图 5 水头压力和上覆应力对Ca2+浓度分布的影响
Figure 5. Influence of the gradient and the confine pressure on the distribution of the Ca2+ concentration
-
[1] 中华人民共和国国家统计局. 中国统计年鉴[M]. 北京: 中国统计出版社, 2020 [2] ZHANG P, WU Z C. Municipal sludge as landfill barrier material[J]. Journal of Environmental Sciences, 2002, 17(1): 474-477. [3] 刘磊, 薛强, 赵颖, 等. 溶质入渗土工合成衬垫的化学-渗透特性研究[J]. 岩土力学, 2012, 33(10): 3025-3066. [4] 卢普伟, 万小明, 王冲, 热带地区城市垃圾填埋场防渗施工技术[J]. 施工技术, 2020, 49(15): 96-98. [5] 段亚萍, 侯立兵, 石志刚, 等. 膨润土产品及制品标准化现状及发展[J]. 中国矿业, 2019, 28(12): 167-175. [6] ROWE R K, BOSTWICK L, THIEL R. Shrinkage characteristics of heat-tacked GCL seams[J]. Geotextiles and Geomembranes, 2010, 28(4): 352-359. doi: 10.1016/j.geotexmem.2009.11.001 [7] AZAD F M, EL-ZEIN A, ROWE R K, et al. Modelling of thermally induced desiccation of geosynthetic clay liners in double composite liner systems[J]. Geotextiles and Geomembranes, 2012, 34: 28-38. doi: 10.1016/j.geotexmem.2012.02.012 [8] BOUAZZA A, GATES W P. Overview of performance compatibility issues of GCLs with respect to leachates of extreme chemistry[J]. Geosynthetics International, 2014, 21(2): 151-167. doi: 10.1680/gein.14.00006 [9] BENSON C H, MEER S R. Relative abundance of monovalent and divalent cations and the impact of desiccation on geosynthetic clay liners[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2009, 135(3): 349-358. [10] ROWE R K, JABIN F. Effect of prehydration, permeant, and desiccation on GCL/Geomembrane interface transmissivity[J]. Geotextiles and Geomembranes, 2021, 49: 1451-1469. doi: 10.1016/j.geotexmem.2021.04.006 [11] 刘玉芹. 天然膨润土矿物防渗材料的性能评价与寿命预测[J]. 中国建筑防水, 2021, 8: 50-53. [12] 李芹, 廖才能, 廖明旭, 等. 赤泥渗滤液对钠基膨润土黏土衬垫的渗透机理分析[J]. 环境工程, 2021, 39(1): 148-153. [13] 陈永贵, 雷宏楠, 贺勇, 等. 膨润土−红黏土混合土对NaCl 溶液的渗透试验研究[J]. 中南大学学报(自然科学版), 2018, 49(4): 910-915. doi: 10.11817/j.issn.1672-7207.2018.04.019 [14] 王宝, 董兴玲. 利用膨润土的膨胀和稠度特征对GCL渗透系数进行预测的试验研究[J]. 土木建筑与环境工程, 2015, 37(5): 66-71. [15] FU X L, ZHANG R, REDDY K R, et al. Membrane behavior and diffusion properties of sand/SHMP-amended bentonite vertical cutoff wall backfill exposed to lead contamination[J]. Engineering Geology, 2021, 284: 106037. doi: 10.1016/j.enggeo.2021.106037 [16] 张虎元, 童艳梅, 贾全全. 强碱性溶液扩散对高庙子膨润土的化学腐蚀[J]. 岩石力学与工程学报, 2020, 39(1): 166-176. [17] 傅贤雷, 杜延军, 沈胜强, 等. PAC 改性膨润土/砂竖向阻隔屏障回填料化学渗透膜效应及扩散特性研究[J]. 岩石力学与工程学报, 2020, 39(S2): 3669-3675. [18] MALUSIS M A, KANG J B, SHACKELFORD C D. Restricted salt diffusion in a geosynthetic clay liner[J]. Environmental Geotechnics, 2015, 2(2): 68-77. doi: 10.1680/envgeo.13.00080 [19] ASHMAWYA K, MUHAMMAD N, ELHAJJI D. Advection, diffusion, and sorption charact- eristics of inorganic chemicals in GCL bentonite[M]. Austin: Waste Containment and Remediation, 2005. [20] 何俊, 施建勇, 廖智强, 等. 膨润土中离子扩散特征试验研究[J]. 岩土力学, 2007, 28(4): 831-835. doi: 10.3969/j.issn.1000-7598.2007.04.039 [21] 侯娟, 滕宇阳, 李昊, 等. 多孔介质曲折度对膨润土衬垫渗透性能的影响[J]. 湖南大学学报(自然科学版), 2022, 49(1): 155-164. [22] LIESKE W, CHRIST F, BAILLE W, et al. Suction and crack propagation in GCLs subjected to drying and wetting in CaCl2-solutions[J]. Geotextiles and Geomembranes, 2020, 48(6): 973-982. doi: 10.1016/j.geotexmem.2020.07.005 [23] 侯晓萍, 樊恒辉. 基于COMSOL Multiphysics的非饱和裂隙土降雨入渗特性研究[J]. 岩土力学, 2022, 43(2): 564-572. [24] 王祥云, 陈涛, 王春丽, 等. 若干重要放射性核素在北山花岗岩及高庙子膨润土中的吸附和扩散研究[J]. 中国科学:化学, 2020, 50(11): 1585-1599. [25] 张文杰, 顾晨, 楼晓红. 低固结压力下土−膨润土防渗墙填料渗透和扩散系数测试[J]. 岩土工程学报, 2017, 39(10): 1915-1921. doi: 10.11779/CJGE201710021 [26] LORENZETTI R J, BARTELT-HUNT S L, BURNS S E, et al. Hydraulic conductivities and effective diffusion coefficients of geosynthetic clay liners with organobentonite amendments[J]. Geotextiles and Geomembranes, 2005, 23(5): 385-400. doi: 10.1016/j.geotexmem.2005.02.002 [27] NOORUDDIN H A, HOSSAIN M E. Modified Kozeny-Carmen correlation for enhanced hydraulic flow unit characterization[J]. Journal of Petroleum Science and Engineering, 2011, 80(1): 107-115. doi: 10.1016/j.petrol.2011.11.003 [28] XU P, YU B. Developing a new form of permeability and Kozeny-Carman constant for homogeneous porous media by means of fractal geometry[J]. Advances in Water Resources, 2008, 31(1): 74-81. doi: 10.1016/j.advwatres.2007.06.003 [29] SHACKELFORD C D, MEIRE A, SAMPLE-LORD K. Limiting membrane and diffusion behavior of a geosynthetic clay liner[J]. Geotextiles and Geomembranes, 2016, 44(5): 707-718. doi: 10.1016/j.geotexmem.2016.05.009 [30] SHAN H Y, LAI Y J. Effect of hydrating liquid on the hydraulic properties of geosynthetic clay liners[J]. Geotextiles and Geomembranes, 2002, 20(1): 19-38. doi: 10.1016/S0266-1144(01)00023-1 [31] ROWE R K. Geosynthetic clay liners: Perceptions and misconceptions[J]. Geotextiles and Geomembranes, 2020, 48(2): 137-156. doi: 10.1016/j.geotexmem.2019.11.012 [32] 郭建春, 庄园, 刘超. 考虑非达西效应的酸蚀裂缝流场数值模拟[J]. 岩土力学, 2015, 36(11): 3315-3321. [33] 侯会明, 胡大伟, 周辉, 等. 考虑细观等效热学参数的高放废物处置库围岩应力-渗流-温度耦合模拟方法[J]. 岩土力学, 2019, 40(9): 3625-3634. [34] 杨盛. 基于COMSOL 模拟开裂混凝土中的氯离子扩散行为[J]. 科技创新与应用, 2020(6): 14-15. [35] 张志红, 师玉敏, 朱敏. 黏土垫层水力-力学-化学耦合模型研究[J]. 岩土工程学报, 2016, 38(7): 1283-1290. doi: 10.11779/CJGE201607016 [36] SHACKELFORD C D, BENSON C H, KATSUMI T, at al. Evaluating the hydraulic conductivity of GCLs permeated with non-standard liquids[J]. Geotextiles & Geomembranes, 2000, 18(2/3/4): 133-161. [37] ASTM D6766-2018. Standard test method for evaluation of hydraulic properties of geosynthetic clay liners permeated with potentially incompatible aqueous solutions-see all versions[S]. American Society for Materials and Testing, 2018. [38] 何俊. 基于微观分析的填埋场GCL中运移规律的理论研究[D]. 南京: 河海大学土木工程学院, 2006. [39] 李学垣. 土壤化学[M]. 北京: 高等教育出版社, 2001. [40] LAKE C B. Contaminant transport through geosynthetic clay liners and a composite liner system[D]. Ontario: The University of Western Ontario, 2001. [41] MALUSIS M A. Membrane behavior and coupled solute transport through a geosynthetic liner[D]. Colorado: Colorado State University, 2001. [42] SHACKELFORD C D, DANIEL D E. Diffusion in saturated soil. I: background[J]. Journal of Geotechnical Engineering, 1991, 117(3): 467-484. doi: 10.1061/(ASCE)0733-9410(1991)117:3(467) [43] JANG Y S, HONG G T. An experimental study on diffusion characteristics of hardened liner materials to inorganic chemicals[J]. Environmental Geology, 2003, 44(5): 599-607. doi: 10.1007/s00254-003-0797-y [44] VAN H A. Properties of self-sealing and self-repairing seals[C]//Sardinia 95, International Landfill Symposium. CISA, Cagliari, 1995. [45] 何俊, 郝国文. 粘土衬垫中渗透系数与扩散系数的关系[J]. 煤田地质与勘探, 2007, 35(6): 40-43. doi: 10.3969/j.issn.1001-1986.2007.06.010 -
点击查看大图
计量
- 文章访问数: 5323
- HTML全文浏览数: 5323
- PDF下载数: 114
- 施引文献: 0
