-
有机氯农药(organ chlorine pesticides, OCPs)普遍具有毒性强、难降解、易富集等特点,且部分OCPs 在低剂量长期暴露条件下仍具有内分泌干扰物特性,给生态环境和人类健康带来巨大的潜在威胁。近年来,随着我国工业化和城市化的快速发展及《斯德哥尔摩公约》[1]的履行,大批OCPs生产企业被关闭,遗留污染场地达1 200多个[2]。这些污染场地往往具有污染浓度高、分布较深等特点,已成为我国环境中重要的OCPs污染源。六六六(hexachlorocyclohexane, HCHs)和滴滴涕(dichlorodiphenyltrichloroethane, DDTs)是2种典型的OCPs。截至20世纪80年代,国内DDTs生产量约占世界总产量的20%,而HCHs生产总量占比高达33%[3-5]。OCPs容易在人体内积累, 造成急慢性毒性、内分泌干扰效应和“三致”效应等危害[6-7]。
许多学者采用化学氧化方法(包括芬顿/类芬顿氧化、活化过硫酸盐氧化、高铁酸钾氧化等方法[8-10])降解DDTs或HCHs。其中,高铁酸钾(K2FeO4)是一种兼具氧化和混凝作用的新型环境功能材料[11-15],且其生成的Fe(Ⅲ)通常为纳米级Fe(OH)3胶体,具有很强的吸附性能。有研究[16-17]表明,K2FeO4对γ-HCH具有较高的降解效率,但对DDTs的降解效果未见报道。过硫酸钠(Na2S2O8)通过热、碱、过渡金属或紫外辐射(UV)等方法活化后,可形成硫酸根自由基(SO4 −·)或羟基自由基(OH·),可以高效氧化降解多种类型的有机污染物[18-20]。有研究[21]表明,纳米零价铁活化过硫酸钠对DDTs具有较好的降解效果。在pH=3.2、Fe2+/Na2S2O8=1∶20时,0.16 mol·L−1的活化过硫酸钠反应24 h,DDTs降解率可达90%[22]。
高铁酸盐和活化过硫酸盐分别对HCHs和DDTs均具有较好的降解性能。由于环境介质中DDTs和HCHs往往同时存在,因此,须寻求HCHs和DDTs的同步降解方法。本研究采用K2FeO4和Na2S2O8组成的双氧化体系,考察了K2FeO4单独处理和K2FeO4/Na2S2O8联合处理对HCHs和DDTs降解效率的影响,分析了HCHs和DDTs在K2FeO4/Na2S2O8双氧化体系中的降解产物,并推断其可能存在的降解途径,旨在利用高铁酸盐降解HCHs和高铁酸盐自身降解产生的Fe2+和Fe3+,活化过硫酸盐以进一步降解DDTs,从而实现对HCHs和DDTs的同步协同降解,为K2FeO4/Na2S2O8双氧化体系在环境修复中的应用提供参考。
全文HTML
-
气相色谱-质谱联用仪(Thermo Trace ISQLT,美国赛默飞科技有限公司);恒温振荡箱(THZ-C,太仓市实验设备厂);分析天平(FA1004N,常州市衡正电子仪器有限公司);pH计(E28-standard,上海梅特勒-托利多仪器有限公司)。
无水硫酸钠(Na2SO4),高铁酸钾(K2FeO4),过硫酸钠(Na2S2O8),硫酸(H2SO4, 98%),氢氧化钾(KOH)均为分析纯,正己烷(C6H14),丙酮(CH3COCH3)均为色谱纯,六六六(HCHs,包括α-HCH、β-HCH、γ-HCH,99%),滴滴涕(DDTs,包括p,p ′-DDD、p,p ′-DDE、o,p ′-DDT、p,p ′-DDT,99%)均为标准样品。
-
单因素实验:量取25 mL去离子水于50 mL锥形瓶中,向其中加入含有7种OCPs、浓度均为1 000 mg·L−1 的混合标准工作溶液;混匀后分别加入K2FeO4和Na2S2O8,于恒温振荡箱中以180 r·min−1振荡12 h,加入10 mL正己烷剧烈振荡2 min,静置分层,取出全部正己烷溶液,过无水硫酸钠脱水;采用0.45 μm针式过滤头过滤,取1 μL溶液进入气相色谱-质谱联用仪(GC-MS),测定7种OCPs的浓度,每个处理重复2次。
多因素实验:采用Design Expert 8.0响应面法的中心组合实验设计,研究K2FeO4投加量、Na2S2O8投加量和溶液初始pH等3个因素对OCPs降解的影响,各实验因素的变化范围和对应的代码见表1。
采用Design Expert 8.0拟合响应值与实验条件之间的关系,根据拟合结果制作Perturbation图和3D响应面图,分别反映实验因素及其交互作用对响应值的影响。利用拟合方程对降解条件进行优化分析,得到实验范围内的最佳降解条件,对该条件下的降解效果进行验证,评估模型的预测能力。
采用GC/MS分析降解液中的7种OCPs残留浓度,并鉴定各OCPs的降解产物。
-
由于7种污染物的降解率各不相同,难于综合评判降解效果,因此,以毒性最强、大鼠急性半致死浓度(LD50)最小的γ-HCH为参照对象,其他6种OCPs统一折算为γ-HCH当量以便于加和,并构建环境风险评价方法。计算方法见式(1)和式(2)。
式中:T为7种污染物的γ-HCH当量之和;Ci为第i种OCP浓度;Li为第i种OCPs的毒性系数;
φ 为总环境风险削减率;T和T0为实验后和实验前7种OCPs的γ-HCH当量,mg·L−1。其中,HCHs和DDTs的LD50和对应的毒性系数见表2。
1.1. 仪器与试剂
1.2. 实验方法
1.3. 评价方法
-
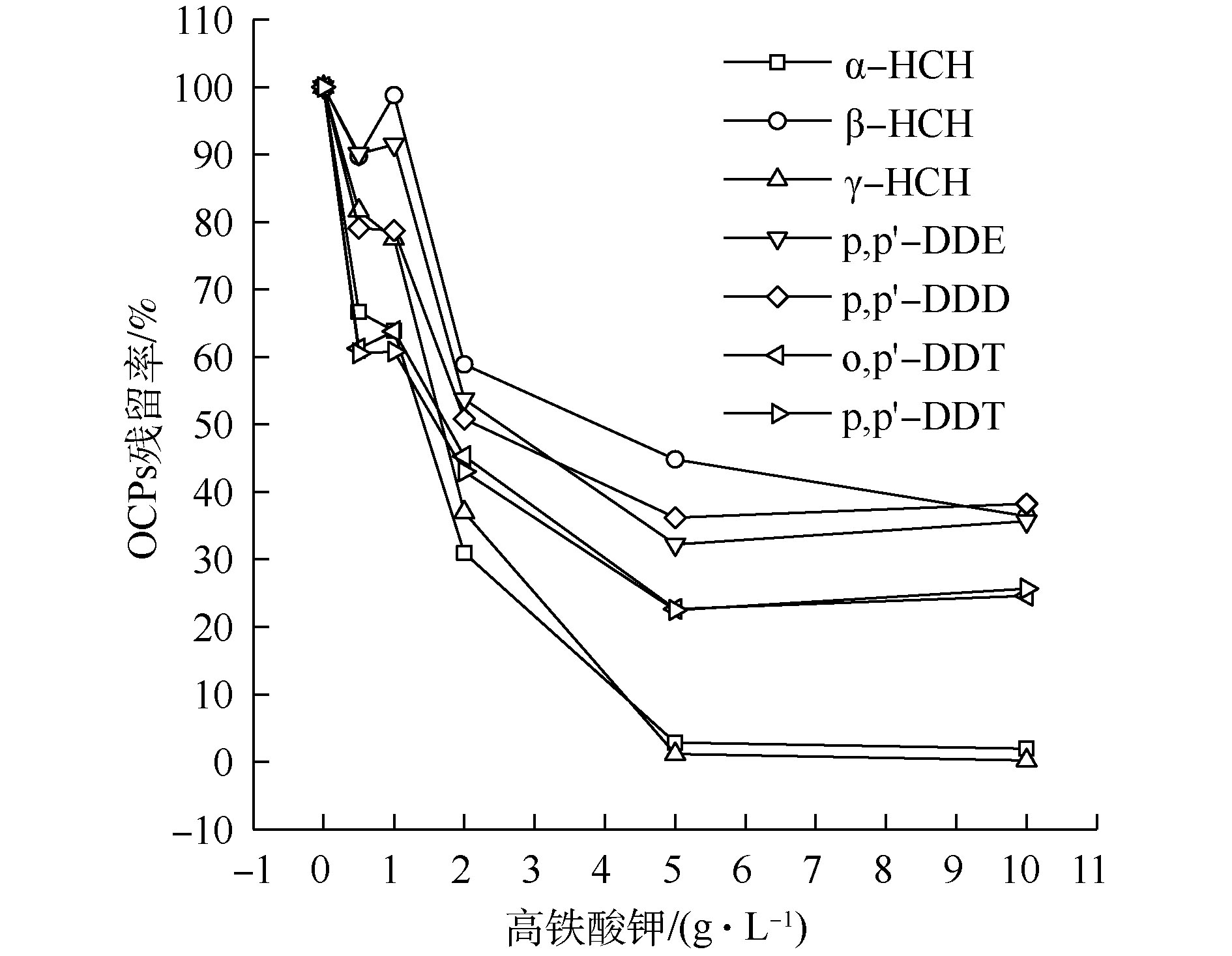
1) K2FeO4投加量对OCPs降解的影响。如图1所示,随着K2FeO4投加量的增加,β-HCH 和p,p′-DDE残留量呈先上升后下降的趋势,其他OCPs降解率则持续升高。当K2FeO4投加量超过5 g·L−1后,OCPs降解率趋于平稳。这可能是由于β-HCH为γ-HCH的降解产物之一,p,p′-DDE为o,p′-DDT或p,p′-DDT的降解产物之一,当K2FeO4投加量较低时,其产生量多于降解量,故有一定程度的积累。当K2FeO4投加量为5 g·L−1时,α-HCH和γ-HCH降解率达到97%以上,但β-HCH降解率仅为44.06%,DDTs降解率仅能达到60%左右。Fe(Ⅱ)投加量过大时,其会成为SO4−·的抑制剂[23-25],并且K2FeO4在浓度过高的时候会自发分解。王立立等[26]研究表明,当K2FeO4浓度超过0.03 mol·L−1时,K2FeO4变得相对不稳定,从而使得OCPs的降解率逐渐平缓甚至有所下降,这与本研究结果相似。此外,K2FeO4投加量的增加会使溶液中碱性增强,导致K2FeO4的氧化电位降低,从而降低了其氧化性能。因此,K2FeO4投加量过高时,OCPs降解率反而有下降的趋势[27]。
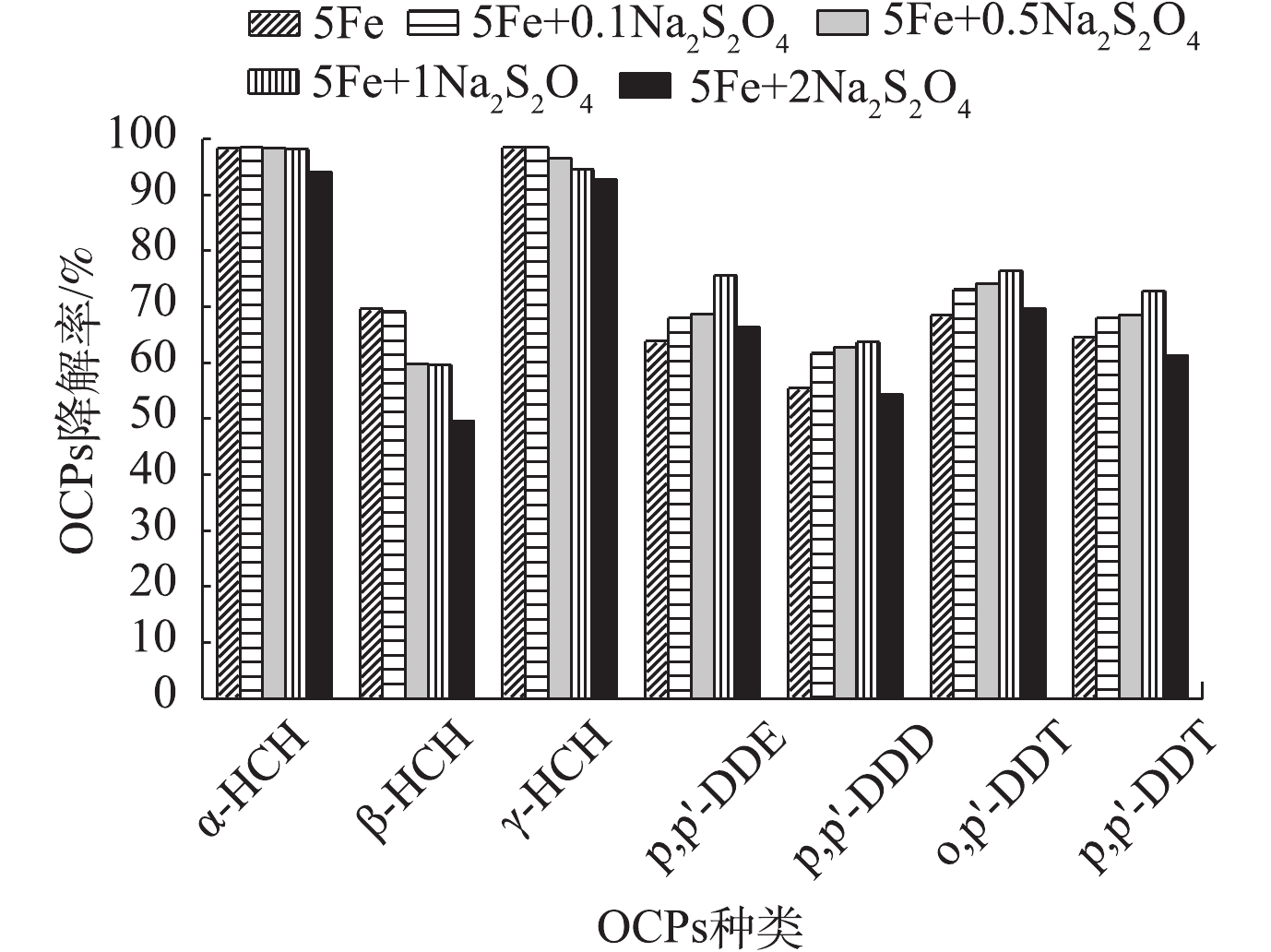
2) Na2S2O8投加量对OCPs降解的影响。由图2可知:当K2FeO4为5 g·L−1时,随着Na2S2O8投加量的增加,HCHs降解率逐渐降低,DDTs降解率先升高后降低;在Na2S2O8投加量为1 g·L−1时,DDTs的降解率达到最高值。这可能是由于HCHs的降解主要来自于K2FeO4氧化,活化过硫酸盐对HCHs的降解效果则较差[28-29];随着Na2S2O8投加量的增加,溶液pH呈下降趋势,因此,不利于K2FeO4降解HCHs。相反,DDTs的降解主要源于活化过硫酸盐氧化,因此,当Na2S2O8/K2FeO4投加量比值最优时,DDTs可达到最高降解率。增加Na2S2O8投加量在一定范围内有利于促进OCPs的降解,但当Na2S2O8过量时,过量的Na2S2O8会消耗SO4−·[30],OCPs的降解率不增反降。
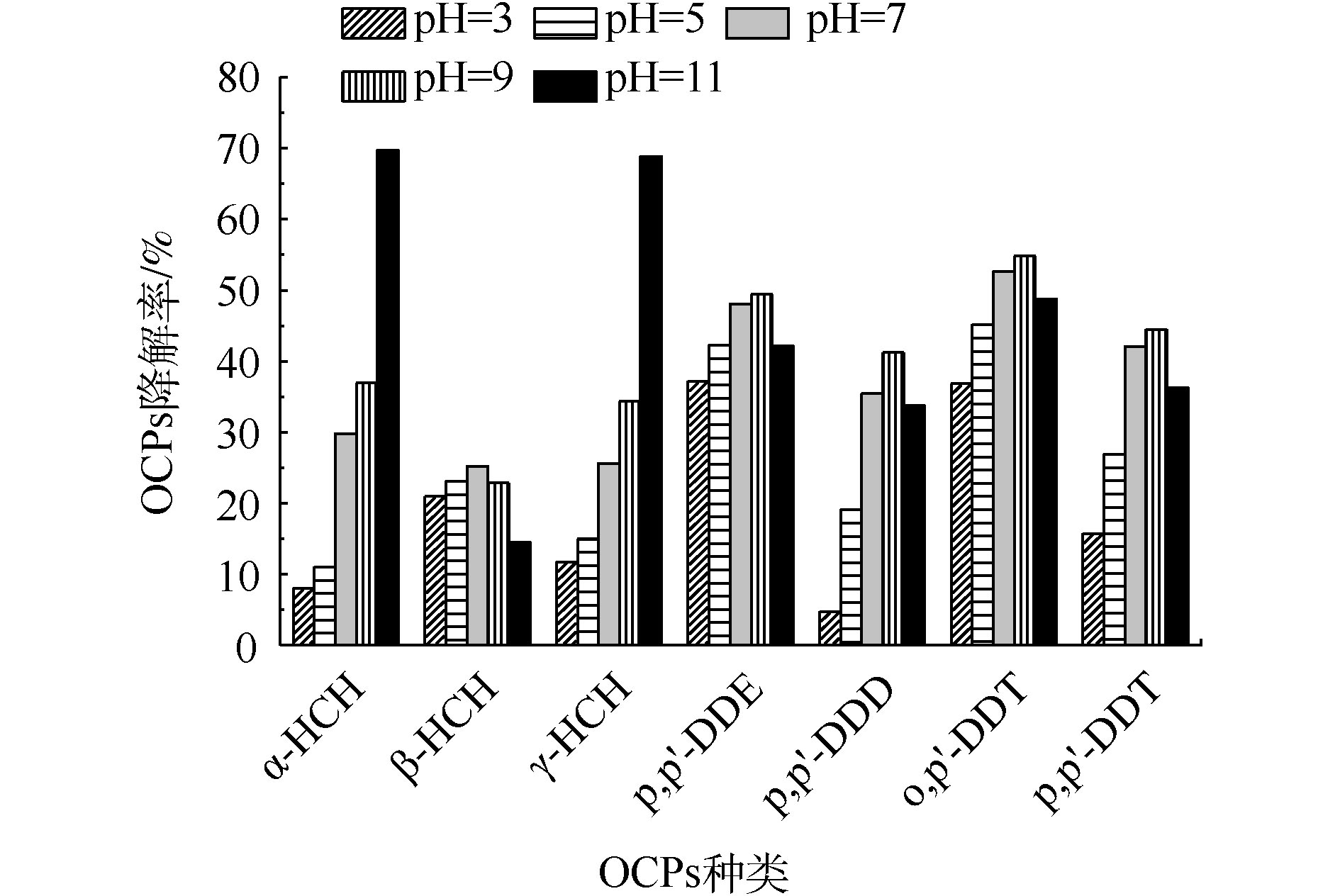
3) pH对OCPs降解率的影响。当K2FeO4投加量为5 g·L−1,Na2S2O8投加量为1 g·L−1时,溶液初始pH对OCPs降解率的影响结果见图3。α-HCH和γ-HCH的降解率随着初始pH的提高而大幅度提升,DDTs的降解率随着初始pH的提高呈先上升后下降的趋势,β-HCH的降解率变化幅度则较小。中性条件(pH=7)时,β-HCH降解效果相对较好,DDTs在弱碱性(pH=7~9)环境中的降解率最高,α-HCH和γ-HCH在碱性环境中(pH=9~11)下降解率较高。
pH对不同污染物呈现出不同的影响,这是因为不同OCPs在该反应体系中的降解机理不同。在酸性条件(pH=3~7)下,K2FeO4氧化性较强,但稳定性较差,容易产生分解;在碱性条件(pH=7~11)下,氧化性较弱,但稳定性较好。α-HCH和γ-HCH在碱性条件(pH=9~11)下具有较高的降解效率,一方面是因为α-HCH和γ-HCH在碱性条件下不稳定,另一方面则体现了K2FeO4在碱性条件的稳定降解能力。其他5种OCPs在近中性或酸性条件下(pH=2~7)降解效果较好。魏海江等[22]发现,活化过硫酸钠在中性(pH=7.7)及酸性(pH=3.2)条件都能有效地降解DDTs,而且中性条件下降解率比酸性条件下高,这与本研究的结果相似。
-
1)模型拟合、方差及显著性分析。根据中心组合设计实验结果(表3),采用Design-Experts 8.0中的二次多项式和逐步回归法拟合响应值(即各OCPs降解率、总环境风险削减率)与实验因素(即降解条件)之间的关系,得到α-HCH降解率(Y1)、β-HCH降解率(Y2)、γ-HCH降解率(Y3)、p,p′-DDE降解率(Y4)、p,p′-DDD降解率(Y5)、o,p′-DDT降解率(Y6)、p,p′-DDT降解率(Y7)和总环境风险削减率(Y8)的模型拟合结果(如表4所示)。
在表3和表4中,A、B和C分别代表K2FeO4投加量,Na2S2O8投加量和pH。模型编号1~8的F值均较大,P值均小于0.000 1,回归模型显著[31],失拟项均不显著(失拟项P>0.05),这表明回归模型正确,实验方法可靠。由于采用逐步回归方法进行模型拟合,确保进入回归模型中的实验因素均为显著(P<0.05)。模型的决定系数R2都在0.90以上,说明模型可靠性强。其中模型1、3、5和8为线性关系,表明各实验因素间不存在显著的互作关系。其他模型包含互作项,表明相应的实验因素之间存在交互作用。
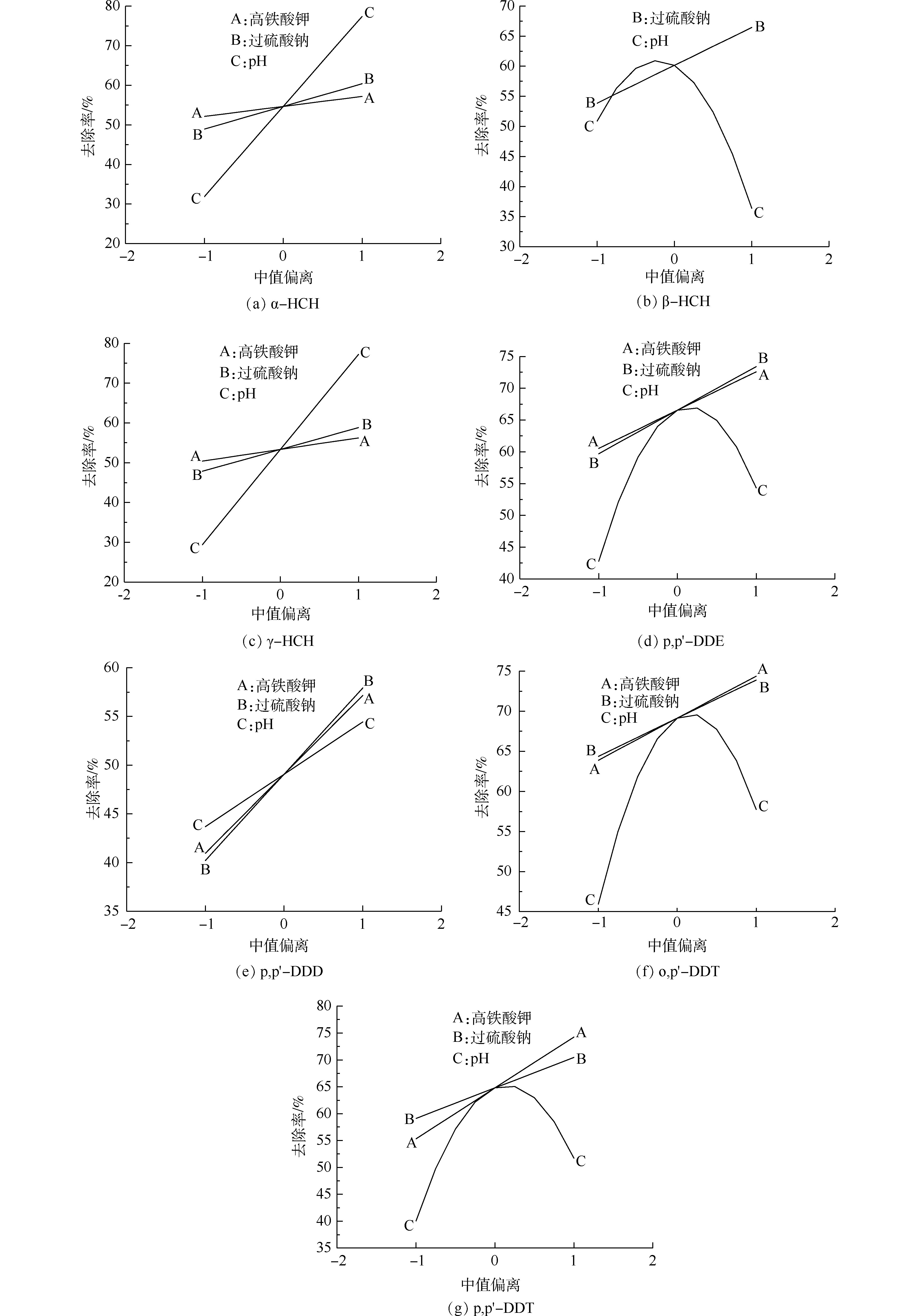
2)敏感性分析。图4反映了其他实验因素取参考点(中值)时,降解条件对各OCPs降解率及总环境风险削减率的影响程度。横坐标中−1和1分别代表最小值和最大值,−0.5和0.5分别代表最小值与中值的均值、中值与最大值的均值。K2FeO4、Na2S2O8投加量对各OCPs降解率及总环境风险削减率的影响效果相似,都随着K2FeO4、Na2S2O8投加量的增加而上升,其中β-HCH降解率不受K2FeO4投加量的影响,pH影响效果显著(图4(b))。
对于K2FeO4,pH影响其氧化性与稳定性之间的消长关系。酸性条件下K2FeO4氧化性较强但稳定性较差,反之碱性(pH=9~11)条件下K2FeO4稳定性较好但氧化能力相对较弱。对于活化过硫酸盐,pH决定了铁活化或碱活化两者之间的消长关系。当pH较高时,碱活化过硫酸盐氧化占优势,铁离子容易沉淀,因此,对过硫酸盐的活化效果较差;反之pH较低时铁活化过硫酸盐氧化占优势。
α-HCH、γ-HCH、p,p′-DDD降解率与3个因素均呈相关关系,表明碱性(pH=9~11)条件下,增加2种氧化剂对于污染物降解均有促进作用,它们主要依赖K2FeO4氧化或碱活化过硫酸钠降解污染物。β-HCH、p,p′-DDE、o,p′-DDT和p,p′-DDT的降解率与溶液初始pH呈抛物线趋势,在弱碱性(pH=7~9)条件下降解率较高。由于单独K2FeO4处理时降解率较低,因此,其降解可能主要源于活化过硫酸钠的氧化作用。当溶液pH=9时,以上4种污染物去除率处于峰值,表明铁活化和碱活化在此条件下达到平衡,均对OCPs降解发挥了一定的作用。
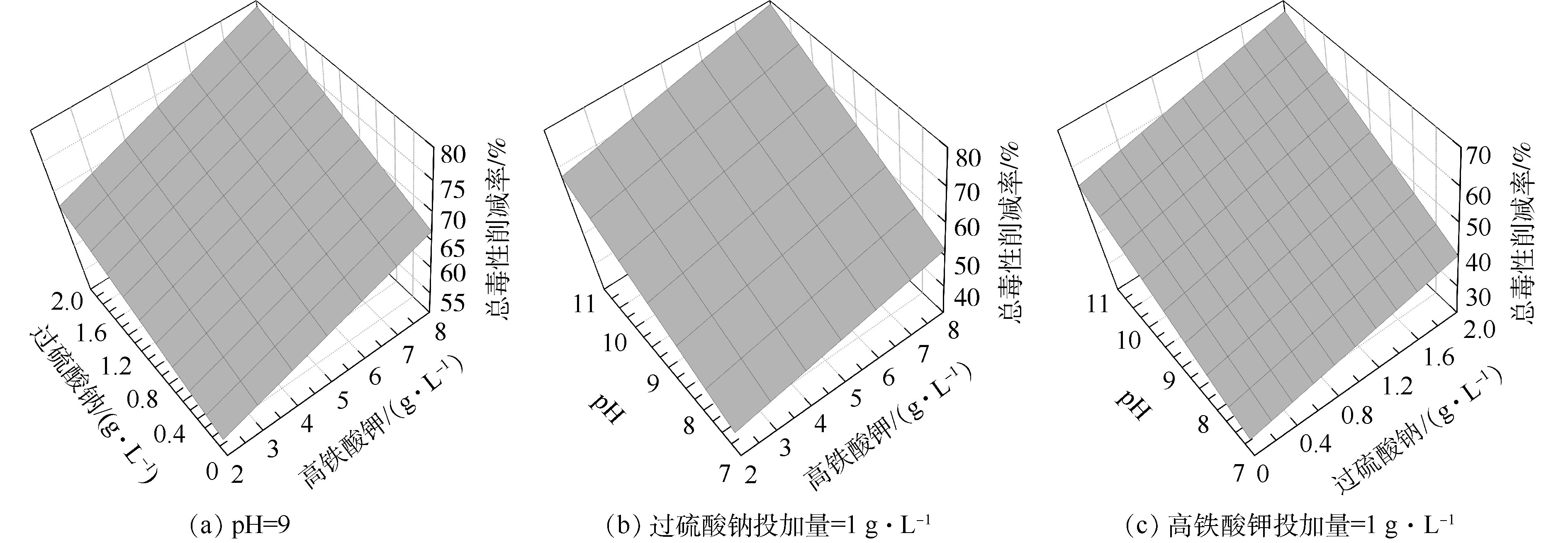
图5(a)反映了初始pH为9时,K2FeO4投加量与Na2S2O8投加量对总环境风险削减率的影响。总体上,总环境风险削减率与K2FeO4投加量、Na2S2O8投加量之间呈线性关系。当K2FeO4投加量一定时,总环境风险削减率随Na2S2O8投加量的增加而缓慢升高;当Na2S2O8投加量一定时,总环境风险削减率也随K2FeO4投加量的增加而缓慢升高,K2FeO4、Na2S2O8投加量对OCPs降解率及总环境风险削减率的影响效果相似。
图5(b)反映了Na2S2O8投加量为1 g·L−1时,K2FeO4投加量与初始pH对环境风险削减率的影响。总体上也呈线性关系。当初始pH一定时,总环境风险削减率也随K2FeO4投加量的增加而缓慢升高,当K2FeO4投加量一定时,总环境风险削减率随初始pH的增加而升高,但初始pH影响幅度较大。
图5(c)反映了K2FeO4投加量为5 g·L−1时,Na2S2O8投加量与初始pH对环境风险削减率的影响。总体上也呈线性关系。当初始pH一定时,总环境风险削减率也随Na2S2O8投加量的增加而缓慢升高,当K2FeO4投加量一定时,总环境风险削减率随初始pH的增加而升高且初始pH影响较为显著。
3) 最优处理条件及验证。以总环境风险削减率最大化为目标对实验条件进行最优化求解。利用Design-Expert 8.0优化得到的最优降解条件为:K2FeO4投加量为8 g·L−1,Na2S2O8投加量为2 g·L−1,pH为11时,总环境风险削减率模拟值为79.16%。根据以上模拟结果,采用Design-Expert 8.0优化得到的最优降解条件进行验证实验,结果如表5所示。与预测值相差较小,误差范围小于5%,预测值和验证值之间存在较好的一致性,表明该模型有较高的可信度和较好的预测能力。
-
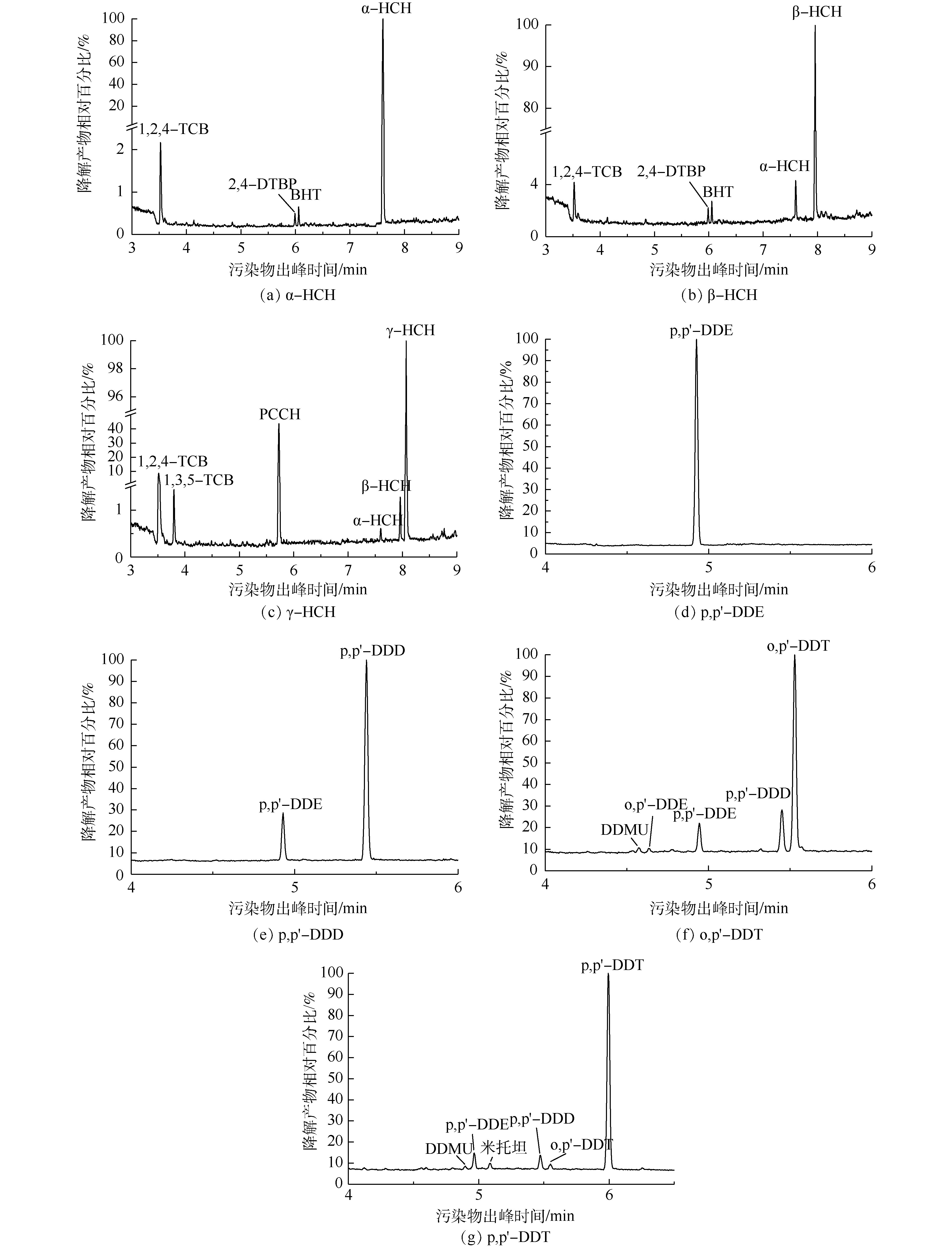
采用Design-Expert 8.0优化得到的最优降解条件分别处理含不同OCPs的水溶液,对降解液进行GC-MS分析,不同OCPs降解液的色谱图见图6。其中图6(a)~(g)分别为α-HCH、β-HCH、γ-HCH、p,p′-DDE、p,p′-DDD、o,p′-DDT和p,p′-DDT降解液的色谱图,共产生了8种降解产物,其基本信息见表6。γ-HCH先转化为α-HCH和β-HCH,接着脱氯脱氢产生PCCH(五氯环己烯)、1,2,4-TCB(1,2,4-三氯苯)和1,3,5-TCB(1,3,5-三氯苯)。LI等[32]发现,β-HCH比α-HCH具有更强的抗降解能力,因此,β-HCH先转化为α-HCH, 再脱氯脱氢产生1,2,4-TCB,接着催化水解氧化生成2,4-DTBP(2,4-二叔丁基苯酚)和BHT(2,6-二叔丁基对甲酚)。p,p′-DDT还脱氯脱氢产生了p,p′-DDD的同分异构体Mitotane(米托坦),o,p′-DDT脱氯脱氢产生了p,p′-DDE的同分异构体o,p′-DDE,二级降解产物均为DDMU。王占杰[33]发现,降解产物DDD比降解产物DDE更易于降解,与本研究结果相符。p,p′-DDE未检测出中间产物,说明降解较为彻底。另外,杨青[34]发现,DDTs(或HCHs)在辐解过程中有Cl·释放,但难以完全脱氯。本研究也检测到未被降解的不完全脱氯产物。
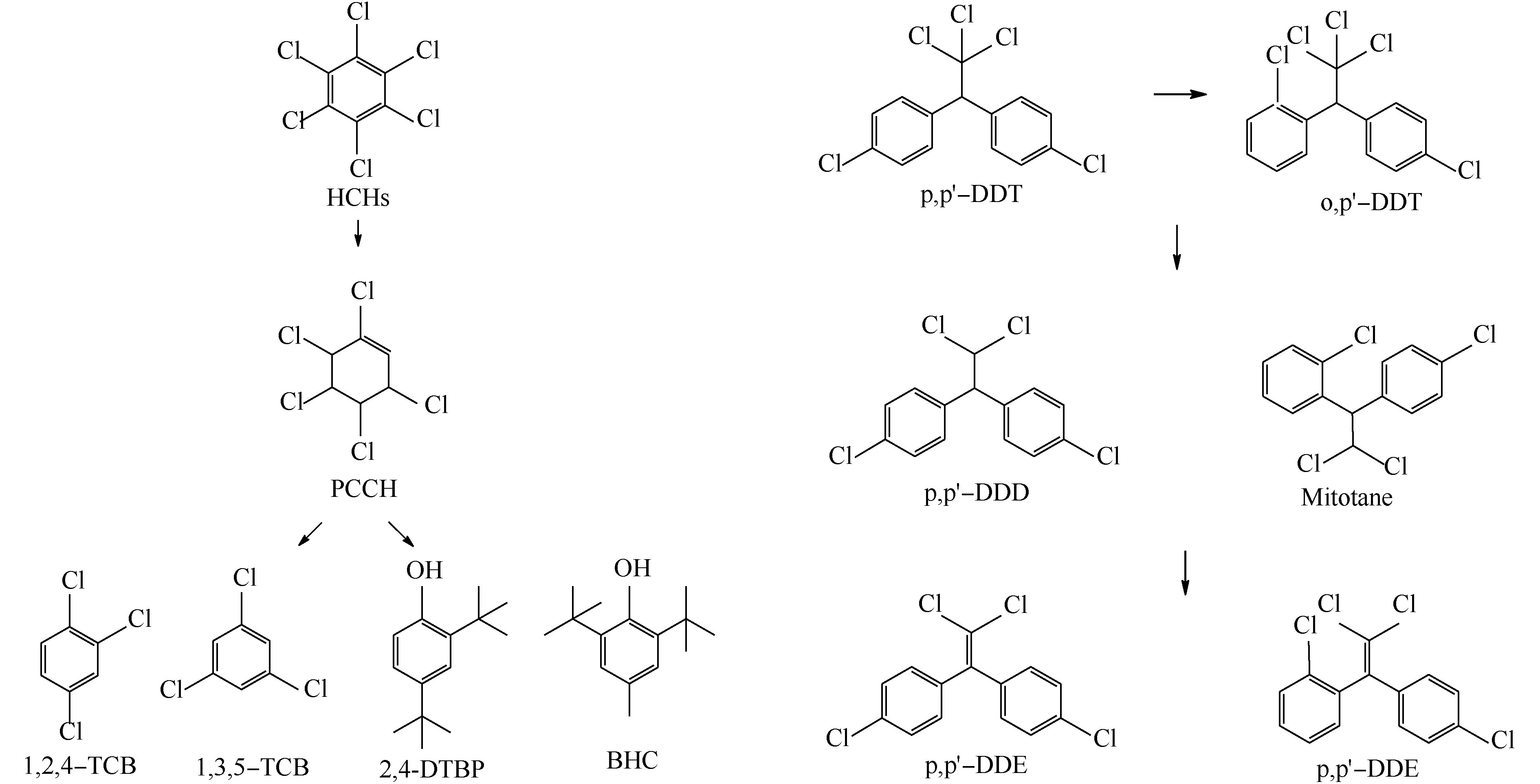
综和上述分析,可推断出K2FeO4/Na2S2O8联合处理对HCHs和DDTs的降解路径图如图7所示。HCHs和DDTs的降解途径主要为脱氯脱氢和水解氧化,p,p′-DDT、o,p′-DDT、p,p′-DDD(或Mitotane)和p,p′-DDE存在依次降解关系。
2.1. 单因素实验
2.2. 多因素实验
2.3. 降解机理
-
1) K2FeO4/Na2S2O8对OCPs的联合降解效果总体上显著优于K2FeO4单独处理的降解效果,中性(pH=7)条件有利于β-HCH的降解,弱碱性条件(pH=7~9)有利于DDTs的降解,而α-HCH和γ-HCH在碱性(pH=9~11)条件下降解效果最显著。
2) α-HCH、γ-HCH、p,p′-DDD降解率和总环境风险削减率与K2FeO4投加量、Na2S2O8投加量和溶液pH的关系呈二次多项式关系,其他OCPs和总环境风险削减率与降解条件呈线性关系,当K2FeO4投加量为8 g·L−1,Na2S2O8投加量为2 g·L−1,pH为11时,总环境风险削减率可达79.16%。
3) K2FeO4/Na2S2O8联合处理对HCHs和DDTs的降解途径主要为脱氯脱氢,但仍存在不完全脱氯产物。其中,HCHs不完全脱氯产物主要为三氯苯和PCCH,次要的水解氧化反应产物为2,4-DTBP和BHT。p,p′-DDT、o,p′-DDT、p,p′-DDD和p,p′-DDE存在依次降解关系。



 DownLoad:
DownLoad: