-
大气边界层(atmospheric boundary layer)为最贴近地面的一层大气,是指直接受地面影响的对流层部分,响应地面作用的时间尺度为一个小时或更短,厚度约为对流层高度的1/10[1-3]。它主要通过摩擦阻力、蒸发和蒸腾、热量输送、污染物排放以及影响气流变化的地形等与地面的作用形成[4-6]。大气边界层内的空气运动由于受到地球自转、温度层结、水汽输送和复杂下垫面等因素的影响而非常复杂[7-8],具有各种气象要素日变化较大、垂直梯度较大等特点,大气边界层高度也随时间和空间不断变化。人类活动带来的污染物排放、传输和转化大部分发生在该层。因此,大气边界层的观测和研究成为大气科学领域的重要内容[9-11]。
常用的提取大气边界层高度手段为:利用常规无线电探空探测的温度、湿度和风廓线计算得到。但是,常规探空探测很难得到高时空分辨率的大气边界层高度信息[10]。近年来,随着遥感技术的迅速发展,激光雷达、微波辐射计和风廓线雷达等高时空分辨率的遥感设备成为估算大气边界层高度的新手段[12-13]。与传统的气象观测手段相比,激光雷达探测大气边界层高度具有时空分辨率高、连续稳定的优势[6]。目前基于激光雷达提取边界层高度的方法包括:目测法、梯度法、标准差法、小波协方差法和线性拟合法。王琳等[4]基于脉冲激光雷达(MPL)数据通过设置不同的尺度间隔研究小波协方差法反演边界层高度的稳定性和准确性,结果表明在尺度间隔﹥300 m时,反演边界层高度趋于稳定。张婉春等[14]基于MPL使用梯度法探测了灰霾天气大气边界层变化特征,发现灰霾天气边界层高度较低。上述对边界层高度的反演都是基于MPL,因激光雷达造价高并未广泛使用。激光云高仪作为一种简易的激光雷达,一般来说探测能力弱于MPL,但与MPL相比造价便宜且体积较小,目前已经广泛应用于全国气象观测网,有较高的时空密度,且污染天气激光云高仪能获得足够的信噪比用于边界层高度的反演[15-17]。
本研究基于Vaisala CL51 云高仪使用梯度法和小波协方差法对2016年10月北京市大兴CL51云高仪后向散射数据进行计算,验证CL51激光云高仪反演边界层高度的可行性,比较梯度法、小波协方差法反演边界层高度的差异,分析不同天气条件边界层高度的日变化,并与探空探测的边界层高度进行对比。
-
Vaisala CL51 云高仪是一种米散射激光雷达,目前在气象探测中主要用于云高、云层和积分云量的测量,其后向散射信号可以反映大气垂直结构。其运用脉冲二极管激光探测和测距技术,短脉冲沿垂直方向发出,在激光脉冲穿过天空时测量光的散射,发射出的激光与大气中的大气分子、气溶胶和水汽等相互作用,后向散射信号被雷达接收系统接收,得到不同高度后向散射回波强度。CL5l激光云高仪激光波长与霾粒子的直径相当,因此产生的散射为米散射,其信号强度的激光雷达方程,见式(1):
式中:
pr(z) 为接收到的瞬时功率;E0 为有效脉冲能量;C为光速;A为接收机孔径;Z为距离;β(z) 为容积后向散射系数;e−2∫z0σ(z')dz' 为大气透过率。CL51激光云高仪光波长910 nm,脉冲频率为10 kHz,峰值功率为27 W,测量高度从地面开始最高达15 km,高度分辨率为10 m,时间分辨率为16 s。CL51激光云高仪与其他的激光雷达相比,云高仪发射的激光功率非常低,后向散射信号容易受到环境噪音的影响。为了提高信噪比CL51激光云高仪采用几束激光脉冲返回信号叠加的总和,高频率的激光脉冲基本消除了伪噪声和高斯白噪声。 -
本研究使用的激光云高仪后向散射资料为北京市大兴区气象局CL51激光云高仪Level2数据,该资料每16 s一组廓线数据,最高高度为4 500 m。所使用的大气成分数据、地面观测数据均为北京市南郊观象台业务观测数据,其中颗粒物质量浓度资料为1小时平均的PM10、PM2.5质量浓度。
-
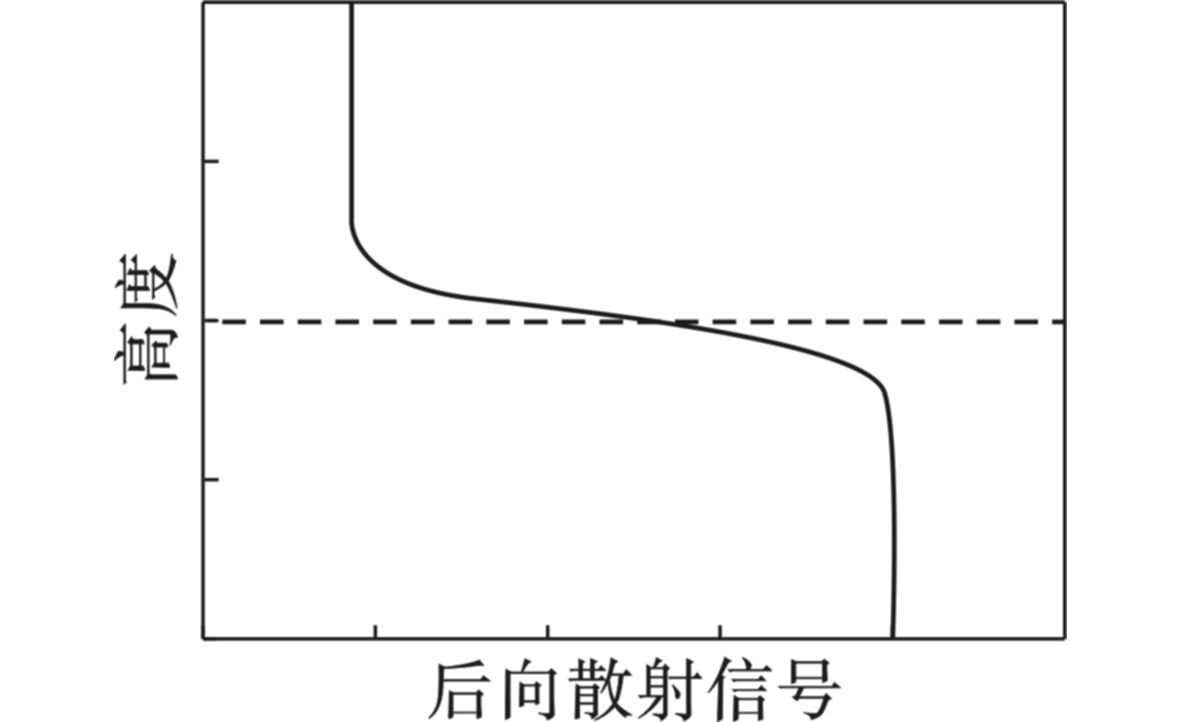
大气边界层顶存在一个逆温层,使得大量的气溶胶粒子聚集在大气边界层内,逆温层以上的自由大气中气溶胶粒子浓度较低。所以在大气边界层与自由大气交界处,气溶胶粒子浓度减小非常快,反映在激光云高仪后向散射信号上,也表现为快速衰减[13]。因此,信号减小最快的高度即可得到大气边界层高度。为理想情况下激光云高仪距离平方校正信号
p(z)z2 廓线图,见图1,虚线为大气边界层高度。图1可知,后向散射信号在大气边界层高度附近减小非常快。
-
梯度法[4]是根据距离平方矫正信号
p(z)z2 随高度的衰减率来判断大气边界层高度。梯度D(z),见式(2):大气边界层高度处于
p(z)z2 衰减最快的位置,也就是取得最大负梯度的高度。这种方法简单方便,但是容易受到环境噪声的干扰,为了减少干扰对结果的影响,本文对p(z)z2 进行了平滑处理,由于王琳等[4]研究表明,平滑点数﹥20时,梯度法反演的边界层高度趋于稳定,故选择的平滑步长为200 m。 -
本研究小波协方差变换使用的是Haar母函数,Haar小波分析法是最早的小波分析方法[7-8],见式(3):
式中:a是Haar函数的振幅;b是Haar函数的中心位置。
小波协方差变换函数
wf() 的定义,见式(4):式中:f(z)为距离平方矫正信号
p(z)z2 ,zt、zb 分别是积分的上限和下限。公式(4)反映的是b高度±a/2范围内的p(z)z2 信号与Haar函数的相似程度。wf(a,b) 越大,相似程度越大,即信号的阶跃性质越明显。wf 取得最大值时的b为大气边界层高度[6]。激光云高仪后向散射信号为离散信号,式(4)可写为式(5):式中,
Δ z是激光云高仪距离分辨率为10 m,a为小波振幅,小波振幅选择300 m。 -
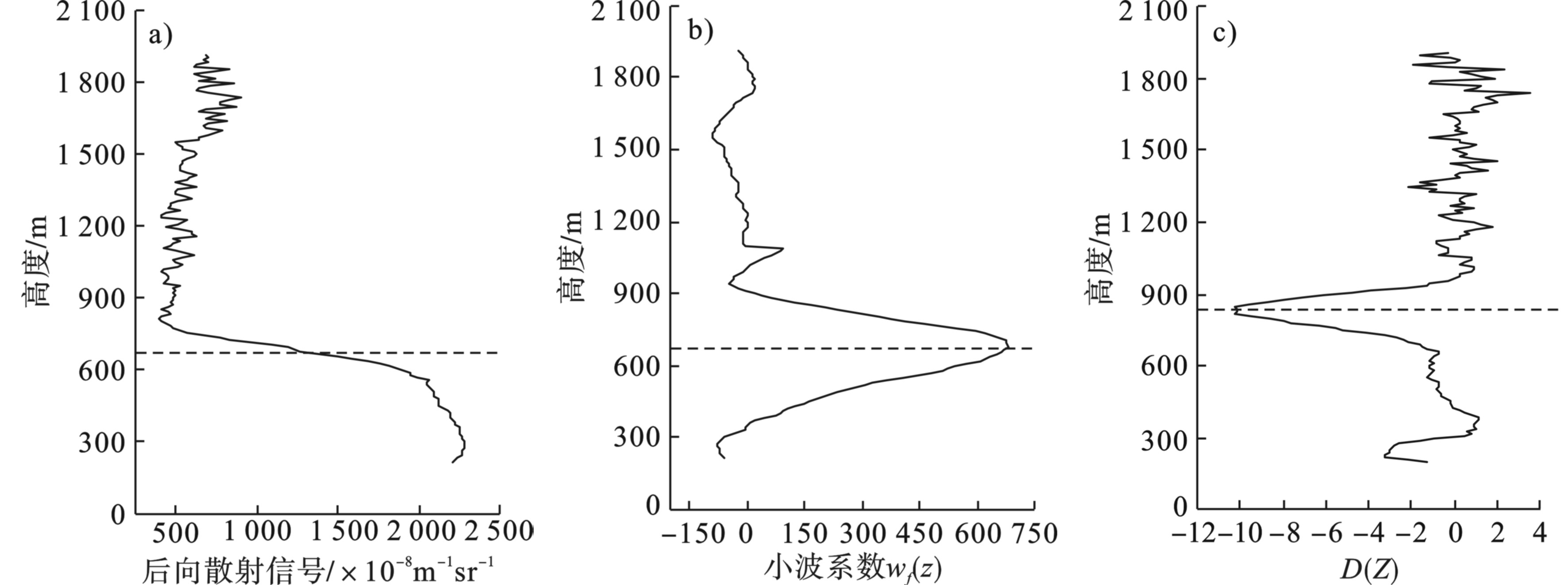
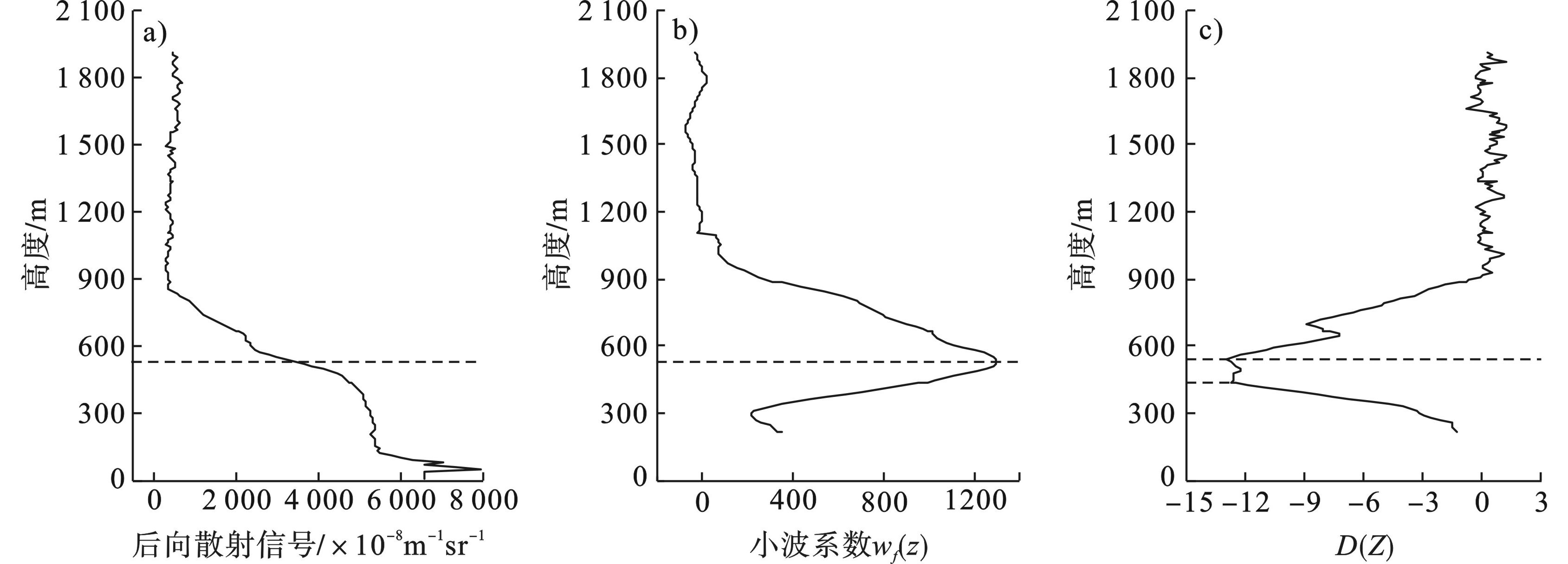
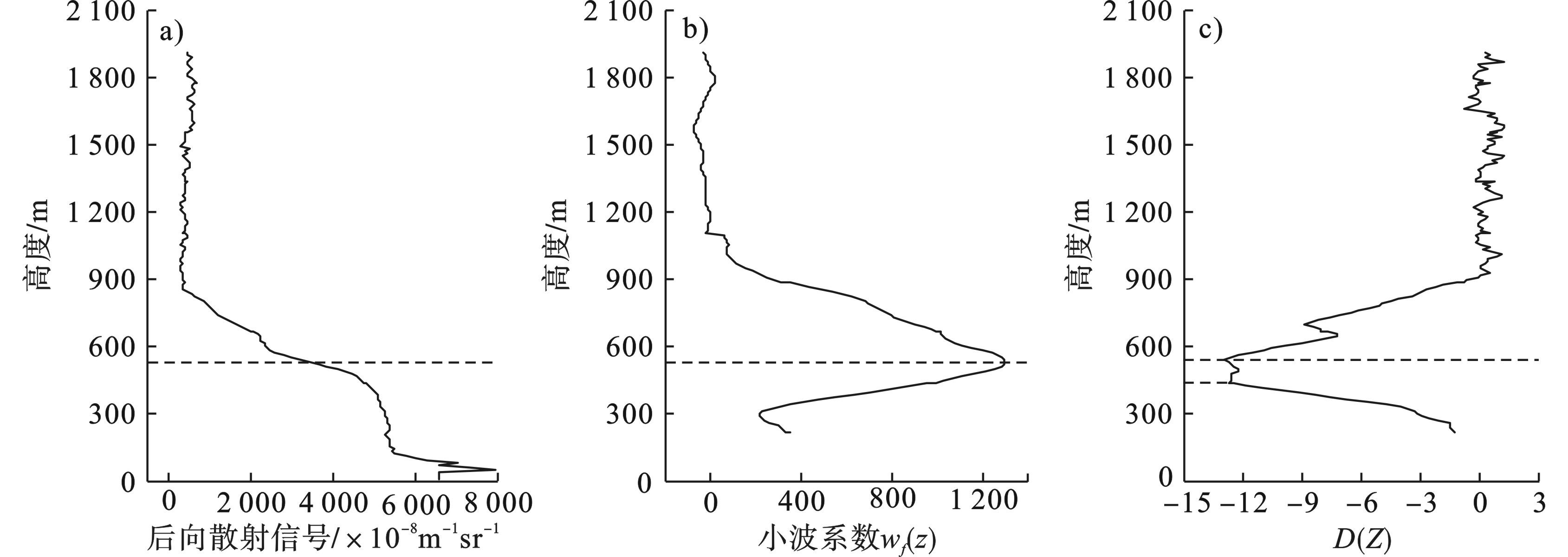
为了研究基于CL51激光云高仪后向散射信号反演大气边界层高度的情况,选择2016年10月5日14:00、2016年10月13日10:30和2016年10月31日10:30 3个时段,使用小波协方差法与梯度法分别计算大气边界层高度,利用后向散射廓线、小波系数廓线和梯度廓线分析2种方法结果的差异。
2016年10月5日14:00、2016年10月13日10:30和2016年10月31日10:30激光云高仪后向散射信号、小波系数和后向散射信号垂直梯度,见图1。2016年10月5日、2016年10月13日和2016年10月31日分别为轻度霾天气、重度霾天气和晴空天气,见图2~图4。
图2(a)可知,后向散射信号在600~750 m高度明显减小,与图1理想后向散射信号在边界层高度附近明显减小相符,后向散射信号在600~750 m高度衰减最快, 可见边界层高度在600~750 m直接;图2(b)小波系数廓线极大值高度为680 m,680 m即小波法反演的边界层高度;图2(c)梯度廓线极小值高度为730 m,730 m即梯度法反演的边界层高度。
图3(a)可知,后向散射信号在450~600 m高度衰减最快,可见边界层高度在450~600 m之间;图3(b)显示小波系数廓线取得极大值的高度为530 m;图3(c)可知,梯度廓线在450和540 m高度均取得极大值,对照后向散射廓线可知540 m处为边界层高度。
图4(a)后向散射信号在高度750~900 m之间快速衰减,对比理想后向散射信号廓线可知,边界层高度就在750~900 m之间。图4(b)小波系数廓线在840 m高度处存在一个极大值,图4(c)梯度廓线存在波动,这是由于后向散射信号廓线存在波动造成的,梯度值极小值760 m即为边界层高度。可见,小波分析法和梯度法都能反映后向散射信号快速减小的位置,但是在提取边界层高度时,梯度法容易受局部气溶胶团的干扰,小波法能更稳定地提取边界层高度。
-
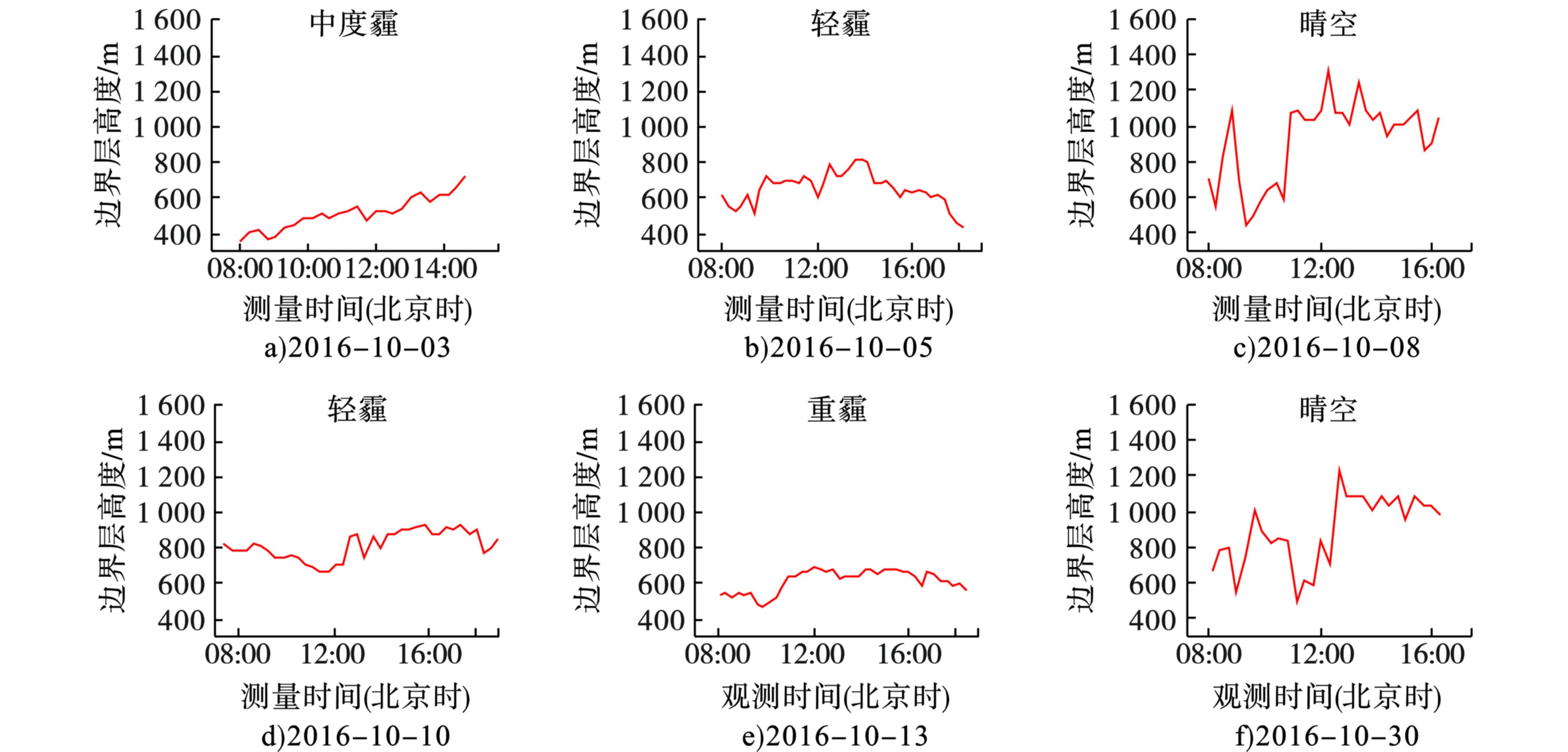
不同天气连续探测边界层高度时序图,可更直观地反映污染天气边界层高度与晴好天气边界层高度的不同特征,见图5。
图5可知,2种方法得到的边界层高度差别不大,但是不同天气边界层高度及其日变化存在明显差异。不同天气边界层高度的差异与地面风速、辐射、湿度和能见度等气象要素息息相关,以下结合地面气象要素分析不同天气边界层高度的差异。2016年10月3日、10月5日、10月10日和10月13日均为霾污染天气,霾污染天气边界层高度均较低,污染程度不同边界层高度日变化也略有差异。
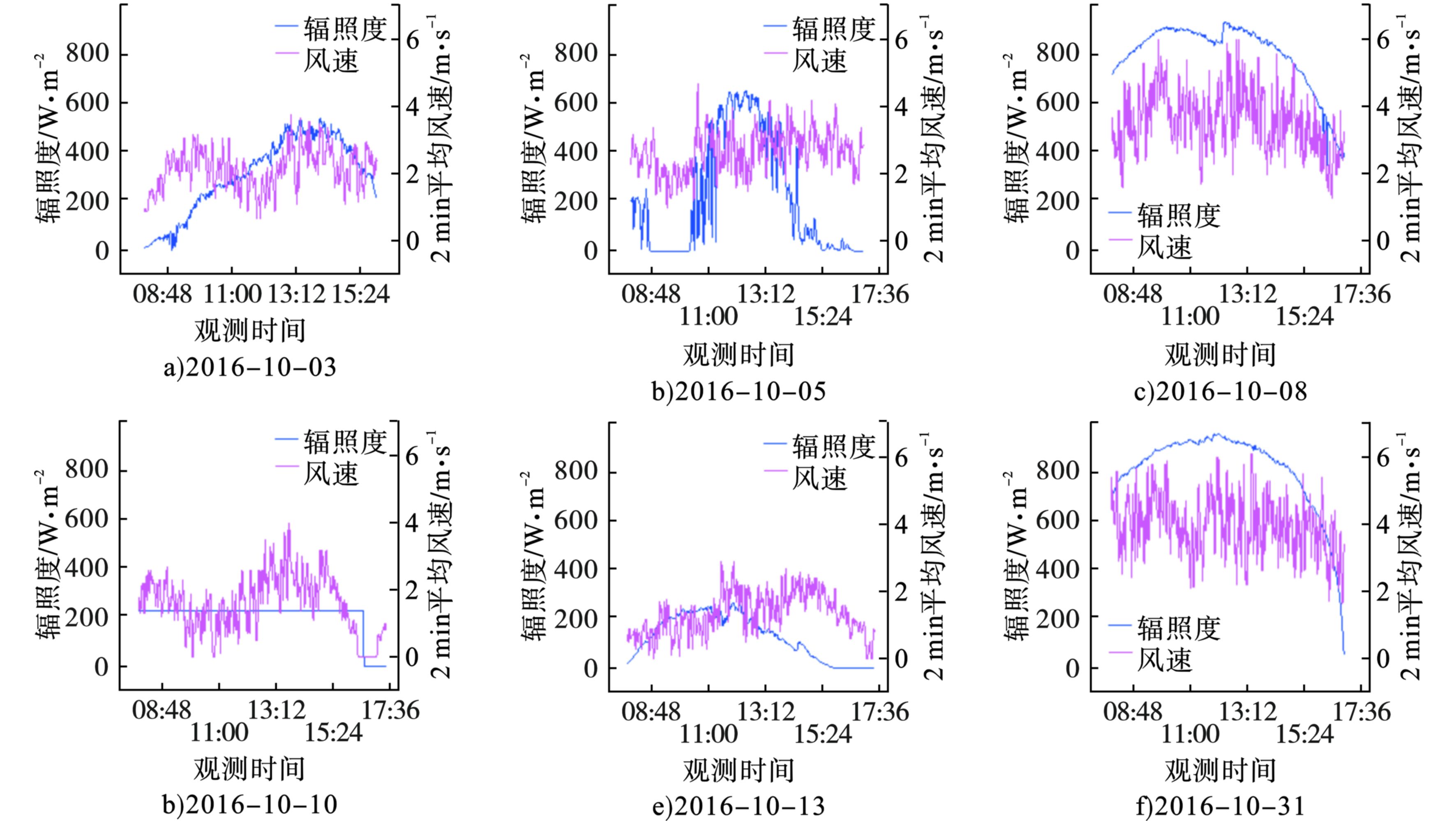
2016年10月3日08:00~14:30,湿度随时间逐渐减小、能见度逐渐增大,由中度霾转为轻度霾,边界层高度逐渐抬升,见图6。
图6(a)可知,研究时段内地面直接辐射值较小,地面风速也较小,地面不具备边界层高度抬升的动力热力条件。但是10月4号凌晨出现了明显降温,上游天气系统破坏了稳定边界层顶的逆温层,故边界层高度随时间逐渐抬升,边界层内的气溶胶粒子发生垂直输送,地面污染逐渐减弱。10月5日、10月10日为轻霾天气,图5(b)、(e)可知,边界层高度分布在400~900 m,低于晴空天气。由于霾对太阳辐射的衰减作用,导致到达地面的太阳辐射较晴空少,地表升温幅度小,正午前后边界层高度抬升幅度较小。10月13日是重度霾污染天气,图5(d)可知,边界层高度较低且没有明显的日变化,集中在400~700 m。重污染天气,边界层内污染物浓度较大,对太阳辐射的吸收和散射作用较强,导致地表接收的太阳辐射较少。图6(d)可知,研究时段内,地面直接辐射值均﹤300
W/m2 ,地面风为不超过2 m/s的小风,不仅地表没有足够的热量使边界层发生明显的抬升,风速较小也不利于污染物扩散,所以边界层高度随时间没有显著变化,且维持在较低高度。图5(c)、(f)是晴空天气边界层高度时序图,边界层高度可达1 300 m,明显高于霾污染天气,边界层高度在正午前后有明显抬升。图6(c)、(f)可知,10月8日与10月31日08:00~16:00时段地面太阳辐射值均﹥600W/m2 ,12:00左右达到最大值,可达900W/m2 。可见晴空天气太阳辐射较强,有利于地表温度增加,增强了湍流作用,使边界层高度抬升。 -
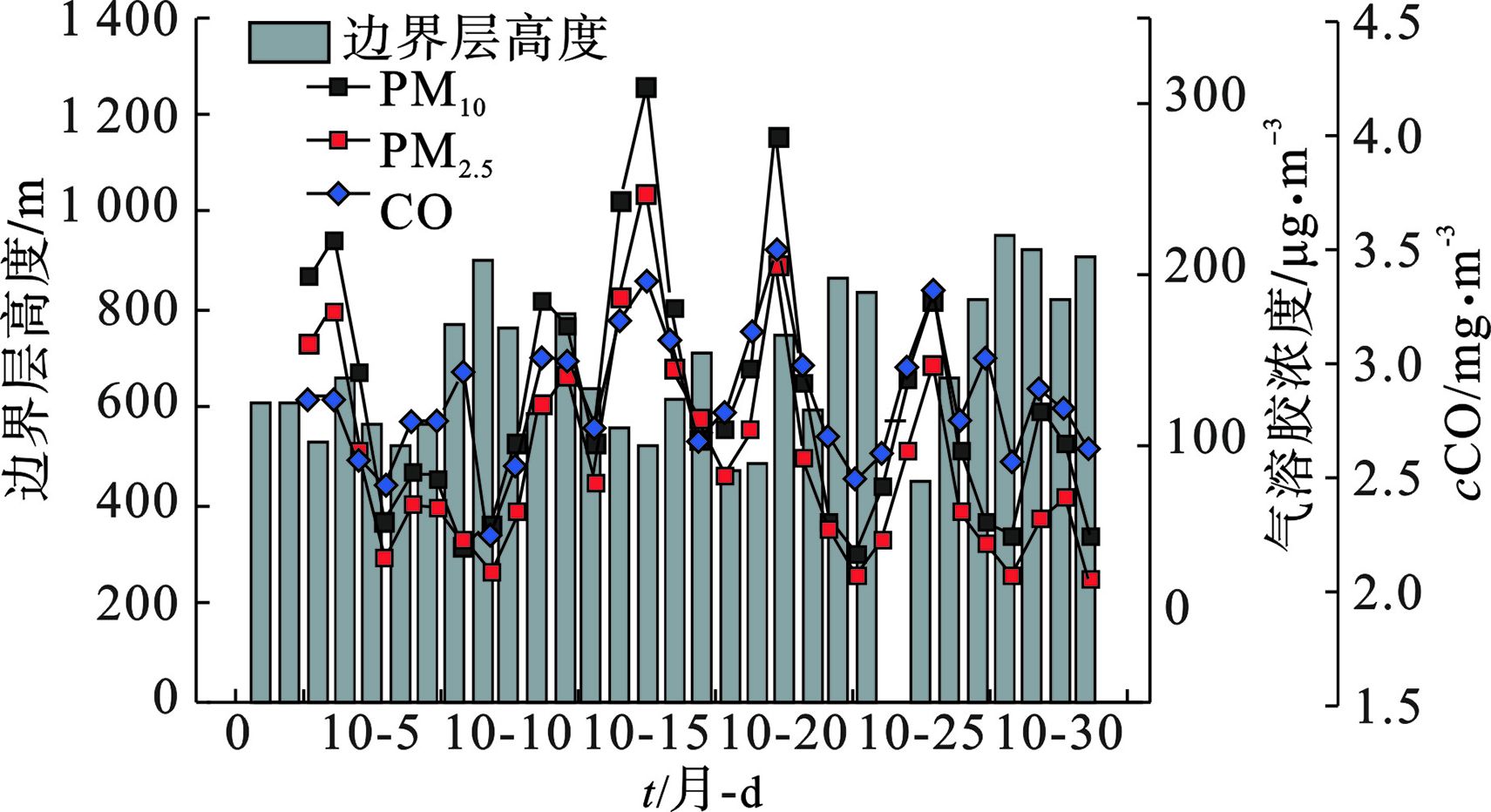
3.2节可知,边界层高度与地面污染有直接的关系,边界层高度决定了污染物在垂直方向上的扩散空间,大气中的污染物通过对太阳辐射的吸收散射作用影响边界层高度的抬升。为了进一步了解各种污染物浓度与边界层高度的相互关系,使用2016年10月激光云高仪探测的边界层高度日平均数据分别与PM2.5、PM10、CO和黑碳等日平均质量浓度数据进行相关性分析。边界层高度与PM2.5、PM10和CO质量浓度的相关系数分别为−0.586、−0.496和−0.528,可见,边界层高度与PM2.5、PM10和CO质量浓度均存在负相关关系,边界层高度与PM2.5浓度相关关系比与PM10浓度相关关系更显著。
2016年10月激光云高仪探测的边界层高度与颗粒物质量浓度变化关系,PM2.5在PM10中占比变化范围为43%~94%,占比平均值为70%,见图7。
图7可知,在空气污染物中,PM2.5颗粒物为主要成分。颗粒物质量浓度较小,边界层高度较高,颗粒物质量浓度较大,边界层高度则较低,边界层高度与PM2.5、PM10颗粒物质量浓度均具有较显著的负相关关系。
黑碳气溶胶(BC)是悬浮在大气中的由含碳物质不完全燃烧产生的黑色碳质颗粒物,是光学法测得的吸光性含碳物质,具有较宽的吸收波段,在可见光和红外波段具有较强的吸收,会影响地面太阳直接辐射。边界层高度与370、470、520、590、660、880和950 nm波段测得的黑碳气溶胶质量浓度相关系数分别为−0.350、−0.242、−0.315、−0.317、−0.317、−0.315和−0.322,可见边界层高度与黑碳气溶胶浓度也具有负相关关系。大气中的黑碳气溶胶通过吸收太阳辐射,削弱到达大气底部的辐射,减小地面增温,进而阻碍边界层高度的抬升,所以黑碳浓度越大,边界层高度越低。
-
激光云高仪作为一种后向散射激光雷达,其后向散射信号可以反映大气垂直结构,可用于边界层高度反演。本研究利用2016年10月激光云高仪数据和探空数据,基于激光云高仪后向散射信号研究了不同天气条件下小波协方差法与梯度法提取边界层高度的差异。并与探空提取结果进行了对比,分析了地面污染对边界层高度的影响。得到以下结论。
(1)通过比较基于激光云高仪的小波协方差法、梯度法,发现2种方法计算的边界层高度差异较小。但在提取边界层高度时,梯度法容易受局部气溶胶团的干扰,小波法能更稳定地提取边界层高度。
(2)霾污染天气,大气中污染物对太阳辐射的吸收和散射,使到达地表的太阳辐射较少,同时加热自由大气,使得大气层结更加稳定,如果没有上游天气系统的影响,不利于边界层内污染物的扩散,边界层高度会维持在较低的高度,边界层高度没有明显日变化。晴空情况下,在正午前后,较强的太阳辐射加热了近地层大气,边界层内湍流扩散旺盛,使大气层结不稳定,边界层发生明显抬升,故边界层高度高于霾污染天气,边界层高度具有较明显的日变化。
(3)大气中的污染物通过对太阳辐射的吸收散射作用影响边界层高度的抬升,边界层高度与PM2.5、PM10、CO和黑碳等污染物质量浓度均存在负相关关系,边界层高度与PM2.5浓度相关关系比与PM10浓度相关关系更显著。
基于激光云高仪探测污染天气边界层高度
Observation of atmospheric boundary layer height of pollution weather with lidar ceilometer
-
摘要: 利用2016年10月北京市大兴CL51云高仪后向散射数据,分别采用梯度法和小波协方差法计算了边界层高度。分析了晴空和霾污染天气边界层高度的差异及影响因素。结果表明,两种方法计算的边界层高度一致性较好。晴空和霾污染天气边界层高度具有不同特征,在霾污染天气,由于大气中污染物削弱了到达地表的太阳辐射,地表没有足够的热量使边界层发生明显抬升,边界层高度维持在较低的高度。晴空天气,由于太阳辐射对地面的增温,边界层高度在正午前后有明显的抬升,边界层高度较高且日变化较明显。边界层高度与地面PM2.5、PM10、CO和黑碳气溶胶等污染物浓度呈负相关关系。Abstract: The atmospheric boundary layer height (ABLH) was calculated by the lidar ceilometer based on the data of Vaisala CL51 ceilometer observed in October 2016 by the Beijing Daxing station. Both the gradient method and the wavelet covariance method were adopted. The atmospheric boundary layer height difference and its influence factors in sunny and haze conditions were analyzed. The results showed that there was no significant difference in ABLH by the two methods. The boundary layer height had different characteristics under different weather conditions. In the case of haze pollution, due to the absorption and scattering of the solar radiation by pollutants in the atmosphere, there was less solar radiation reached the earth surface, the ABLH was lower because of the less heat. While in sunny days, because of the warming of the earth by the solar radiation, the ABLH was higher than that of haze days, and the daily variation of ABLH was more obvious. The ABLH was negatively correlated with the concentrations of PM2.5, PM10, CO, black carbon aerosol and other pollutants on the ground.
-
近年来,袋式除尘器可实现对超细微颗粒的高效处理,且具有运行稳定、造价低廉等优点,已被广泛应用[1]。然而,袋式除尘器体积庞大,占用空间较大[2]。滤筒除尘器是袋式除尘器的一种,具有过滤比表面积更大、阻力低、占地空间更小、安装便捷、易于检修等优点。近年来,通过设计优化和过滤材料更新,滤筒除尘器的处理含尘气量有了巨幅提升,其应用更广泛,在经济性和过滤效率方面都超越了传统袋式除尘器。目前,大部分相关研究集中在立式滤筒除尘器和滤筒清灰方面,而对卧式滤筒除尘器的研究较少。胡家雷等[3]在对滤筒进行脉冲清灰时发现喷嘴长度和喷嘴收缩角对清灰均匀性有显著影响。郗元等[4]运用CFD软件模拟了不同结构滤筒对除尘器内部流场的分布影响,为提高除尘效率,建议选用矩形或圆柱滤筒作为滤芯。刘侹楠[5]模拟了不同进气方式的卧式滤筒除尘器,并添加不同形式导流板进行优化设计,最终使内部流场达到设计标准。袁娜等[6]探究了不同角度挡板对卧式滤筒除尘器内部流场的影响,发现挡板角度为165°~170°时,气流能达到均匀的标准。
卧式滤筒除尘器为立式滤筒除尘器的改进设计,可应用于空间高度受限场所。当含尘气流从除尘器顶部入口进入后,较大粉尘颗粒在重力作用下顺沿气流方向或碰撞到壁面后沉降至灰斗,细微粉尘颗粒则随气流通过滤筒时被拦截在滤筒表面。在过滤过程中,除尘器内部结构对气流组织有着重要作用[5]。因为各除尘器结构不同,导致其内部流场也差别较大,而通过实验来优化除尘器设计不仅耗费时间,且效果不尽人意。运用相关软件进行数值模拟,可直观测得除尘器内部流场特征,且节省时间并降低投资成本[7]。因此,近年来该方法已得到广泛应用。
本研究运用Fluent等软件对现有卧式滤筒除尘器进行数值模拟,探索在不同类型挡板和导流板下除尘器内部的气流组织情况,以期获得最优流场状态,进而为除尘器的结构优化提供参考。
1. 数值模拟
1.1 模型建立与网格划分
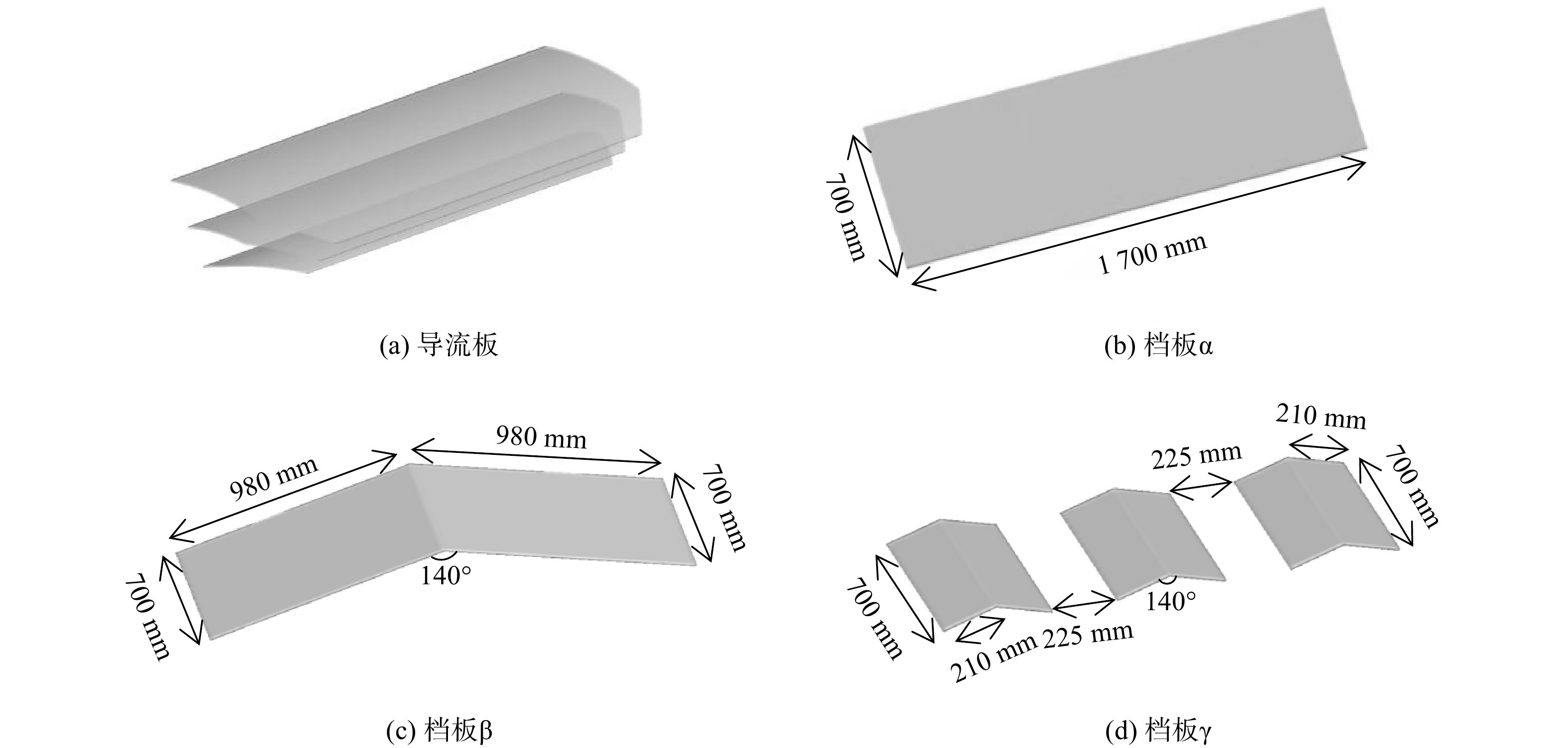
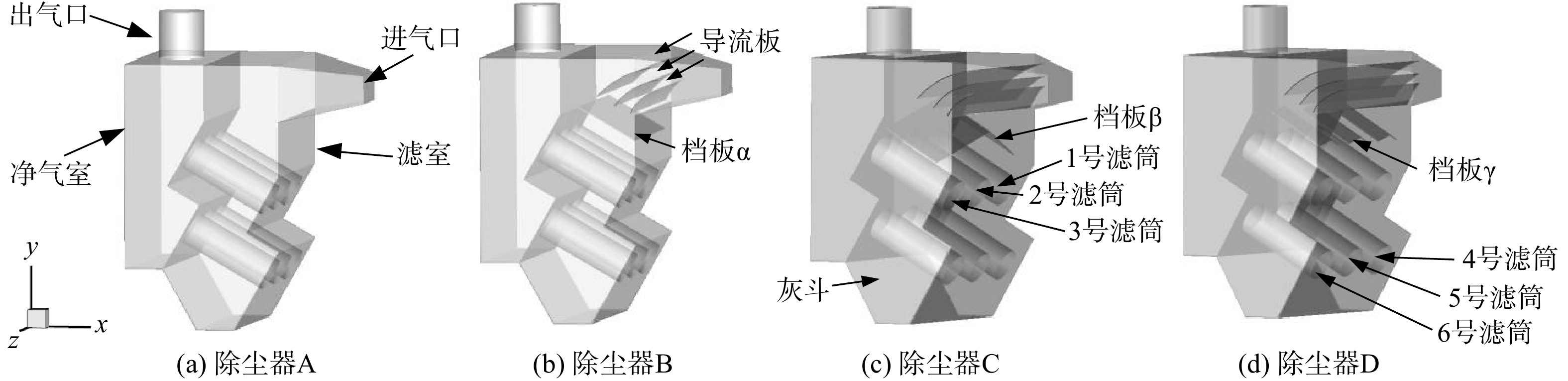
本研究采用的卧式滤筒除尘器由箱体、脉冲清灰系统和滤筒组成。在不影响模拟结果准确性的前提下,取消清灰系统并将滤筒简化为圆柱形[8]。运用ANSYS进行建模,建立如图1所示的4个侧进气卧式滤筒除尘器模型。这4个模型主体尺寸相同,长1 687 mm,宽2 000 mm,高3 330 mm。除尘器内有6个滤筒,其规格为φ360 mm×1 000 mm。滤筒间距为260 mm,两侧距壁面200 mm,上下2层滤筒间隔332 mm。除尘器A为常规卧式滤筒除尘器。除尘器B、C、D在入口处添加了导流板和各类型挡板。其中,3种除尘器的导流板相同,各挡板位于滤筒正上方相同位置,在y方向上投影面积相同。
图2(a)为导流板形状。除尘器中的挡板尺寸如图2(b)~(d)所示。挡板α尺寸为700 mm×1 700 mm;挡板β的夹角为140°,单块的尺寸为700 mm×980 mm;挡板γ由6块小挡板组成,各夹角为140°,单块尺寸为700 mm×210 mm,挡板间距为225 mm。使用Gambit划分网格,采用结构化与非结构化相结合的形式进行网格划分。为提高模拟结果的合理性,对进出口、导流板、挡板、滤筒区域网格进行了加密,并对网格独立性进行了验证,最终选取网格数约381×104的模型进行模拟。
1.2 边界条件设置与求解计算
利用Fluent 18.0软件模拟卧式滤筒除尘器内部流场。入口设为velocity-inlet,速度10 m·s−1;出口设为outflow,滤料厚度为2 mm。滤筒模型边界设为porous-jump,渗透率为6.418×10−12 m2,压力跃阶系数C2取0。其余边界条件如导流板、挡板、净气室、进出口壁面均设置为壁面。气体设为常温常压不可压缩流体[9]。使用压力基稳态求解、湍流模型为k-ε 双方程模型,压力-速度耦合方式为SIMPLE。数值模拟中的连续性方程与动量守恒方程为式(1)和式(2)[10]。
∂(ui)∂xi=0 (1) ∂∂xi(ρuiuj)=−∂p∂xi+∂∂xj(μeff(∂ui∂xj+∂uj∂xi))+ρgi (2) 式中:p为静压;μeff为有效粘度系数;gi为重力加速度分量。
湍流模型采用标准 k—ε模型。湍动能方程与湍动耗散率方程见式(3)~(4)。
∂(ρkui)∂xi=∂[(μ+μσk)∂k∂xj]∂xj+Gk−ρε (3) ∂(ρεui)∂xi=∂[(μ+μtσε)∂ε∂xj]∂xj+C1εεkGk−C2ερε2k (4) 式中:C1ε、C2ε为常量;Gk是由于平均速度梯度引起的湍动能k的产生项;σk 和 σε 是k方程和ε方程的湍流Prandtl数。
滤筒为多孔介质阶跃模型(porous-jump model),压降方程见式(5)。
Δp=−(μαv+12C2ρv2)Δm (5) 式中:α为渗透率;C2为内部阻力系数;Δm 为滤筒厚度。由于过滤风速低,滤筒厚度为2 mm,故忽略第二项内部阻力[10]。
2. 模拟结果与分析
2.1 除尘器内部流场分析
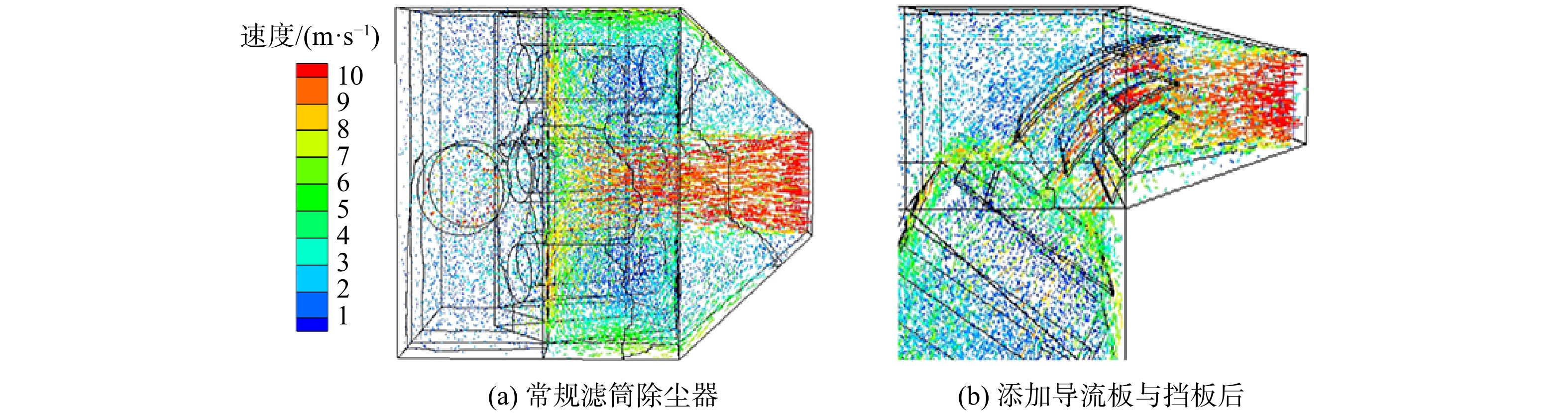
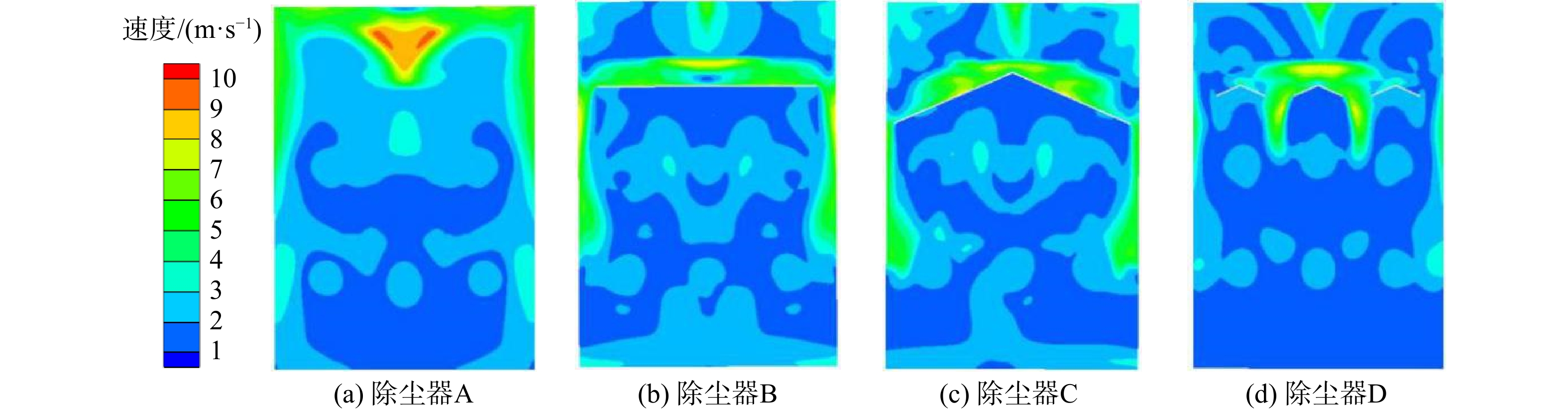
图3为常规滤筒除尘器入口处气流速度矢量俯视图,以及添加导流板、挡板后的局部气流速度矢量图。由于该卧式滤筒除尘器滤筒放置位置较为特殊,特选取如图4(a)~(d)所示x=1 236 mm处平面,以及与图5(a)~(d)所示垂直滤筒上方100 mm处截面速度云图来分析其内部流场情况。从图3(a)中气流速度矢量图可观察到,当入射气流进入除尘器A中,因无导流板作用直接撞击内部墙体,导致气流方向改变,部分气流在除尘器顶部形成涡流使除尘器四周壁面流速较快,平均速度为7.25 m·s−1(见图4(a))。图5(a)中除尘器A壁面流速同样过高,与图4(a)情况相符,滤筒顶部气流达8.60 m·s−1。这是由于另一部分入射气流方向改变后,直接顺沿壁面向下运动抵达滤筒顶部,动能较高。综合图3(a)、图4(a)、图5(a)可发现,除尘器A中内部流场较为紊乱,上层滤筒间隙风速过快,平均风速为5.63 m·s−1。风速过快会导致二次扬尘,且滤筒局部风速不均。长期在此条件下运行,部分滤筒会率先破损和堵塞,从而影响除尘效果。
改善除尘器内部流场均匀性的方法主要是增加功能各异的挡板与导流板,并通过阻挡、分流等功能,使气体的流动规律被强制改变[11]。图3(b)为除尘器安装导流板与挡板后的局部速度矢量图。由图3(b)可知,气流从入口进入除尘器经导流板与挡板作用后,方向发生了改变,并观测到无高速气流直接冲刷除尘器的主体结构。由于导流板的存在,除尘器B、C、D顶部当涡流消失。除尘器B、C、D在x=1 236 mm处平面的速度云图见图4(b)~(d)。由图5可知,加入各类型挡板后,壁面风速有所降低。挡板下方的气流速度存在明显的跳跃边界,滤筒间隙风速较除尘器A降低,内部流场在挡板作用下更加均匀。
如图4(b)与图5(b)所示,除尘器B在挡板α作用下,仅1号、3号滤筒两外侧附近流速较高。这是因入口气流撞击挡板后沿四周扩散导致,平均速度约为6.80 m·s−1,剩余区域滤筒间隙风速约为3.50 m·s−1。图4(c)与图5(c)为除尘器C在挡板β作用下的速度云图,整体效果与挡板α相似,但1号、3号滤筒外侧附近流速较高部分减少,滤筒底部出现较大范围的流速过快区域。其原因是:挡板β存在一定的倾斜角度,当入射气流经过导流板抵达挡板β,动能损失较挡板α小,部分气流沿倾斜角度运动导致滤筒底部风速较快,平均风速约为6.50 m·s−1,其余部分滤筒间隙风速约为3.20 m·s−1。除尘器D在分离式挡板γ作用下的速度云图如图4(d)与图5(d)所示。因为挡板γ由6块小挡板组成,流速较快区域出现在中间挡板两侧,除尘器壁面风速过高情况消失。由图5(d)可知,除尘器D内部的流场气流组织较为均匀,整体变化幅度不大,滤筒间隙平均风速约为3.40 m·s−1。对于滤筒除尘器而言,在合理范围内提高流场速度有利于提高除尘器的工作效率。
2.2 滤筒表面的风速
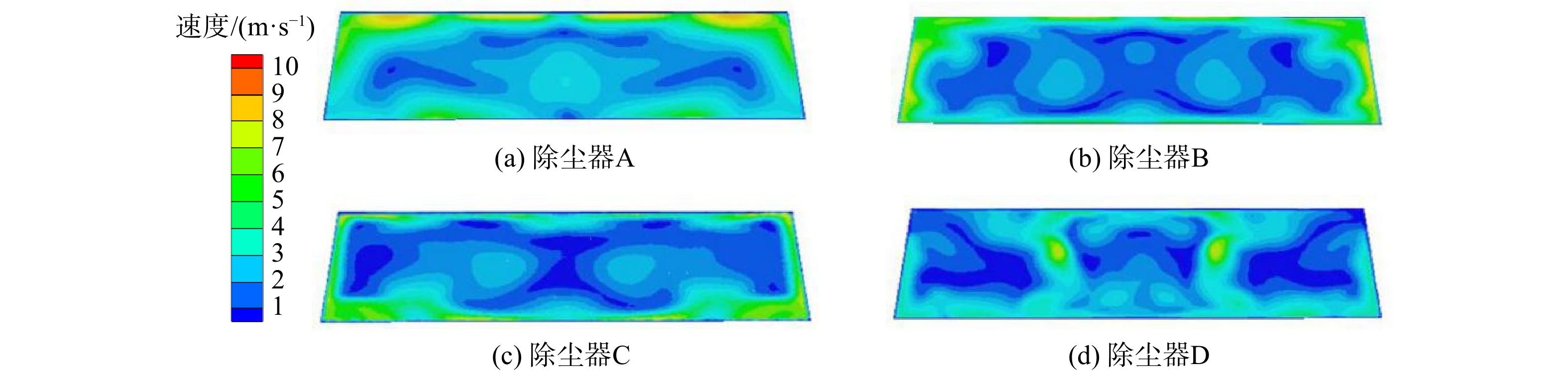
滤筒是除尘器工作的最核心部件。由于无法直接测出过滤风速,在其他条件不变的情况下,滤筒表面风速与过滤速度呈线性相关,通过Fluent软件观测各部位流速特征,可分析滤筒内的过滤情况。在本除尘器中,到达滤筒区域的速度方向主要为竖直方向。滤筒磨损程度主要与该方向速度有关,速度越大,滤筒正面受冲击就越严重[12]。根据能量守恒原理,滤筒表面速度分布不均,会导致滤筒各部位内外压差偏大。另外,在实际运行中,速度较快部位的粉尘层会越积越密,使得滤筒内外压差进一步变大,进而造成粉尘颗粒被挤压至滤筒中,导致颗粒逃逸,分离效率下降,最终出现破洞。图6(a)~(d)分别为卧式滤筒除尘器A、B、C、D滤筒部分的表面风速云图。
由图6(a)可发现,除尘器A为常规卧式滤筒除尘器,无导流、阻流措施,气体进入除尘器撞击墙体后四处逸散,导致上层滤筒表面风速较为紊乱。2号滤筒表面风速较快,大部分区域在3.10 m·s−1。1号、2号、3号滤筒首尾两端最高速度达6.30 m·s−1。由于气流进入除尘器后,气体方向改变,部分气流顺沿壁面到达滤筒顶部,使得气流速度较高。然而,入口喇叭管存在一个向下倾斜的角度,气流沿管道向下运动以较高的速度冲击滤筒末端,导致流速过快。除尘器A中,上层滤筒首尾两端和2号滤筒受冲击程度严重,压力分布不均,长期如此会导致这些部位破损[13]。图6(b)表明,在除尘器B入口设置导流板和挡板α后,射流现象消失,气流经导流板撞击挡板后向四周扩散,导致上层滤筒外侧与末端风速较高,约为4.50 m·s−1。其余区域速度为1.28 ~2.80 m·s−1,较除尘器A的情况有所优化。如图6(c)所示,除尘器C在添加导流板和挡板β后,上层滤筒底部表面风速过高,最高流速达7.50 m·s−1,效果较差。这与较大挡板夹角在165°~170°时,能更好地使除尘器内部气流组织达到均匀相符[6]。图6(d)表示除尘器D在导流板和分离式挡板γ综合作用下的滤筒表面风速情况,其整体均匀,1号、3号滤筒顶部内侧风速为2.40 m·s−1,底部风速约为3.10 m·s−1,其他滤筒区域表面速度为1.13~2.26 m·s−1。综合除尘器A、B、C、D平面速度云图与滤筒表面速度可知,分离式挡板γ能较好地优化侧进气卧式滤筒除尘器内部气流组织。
2.3 滤筒中流量分配的均匀性
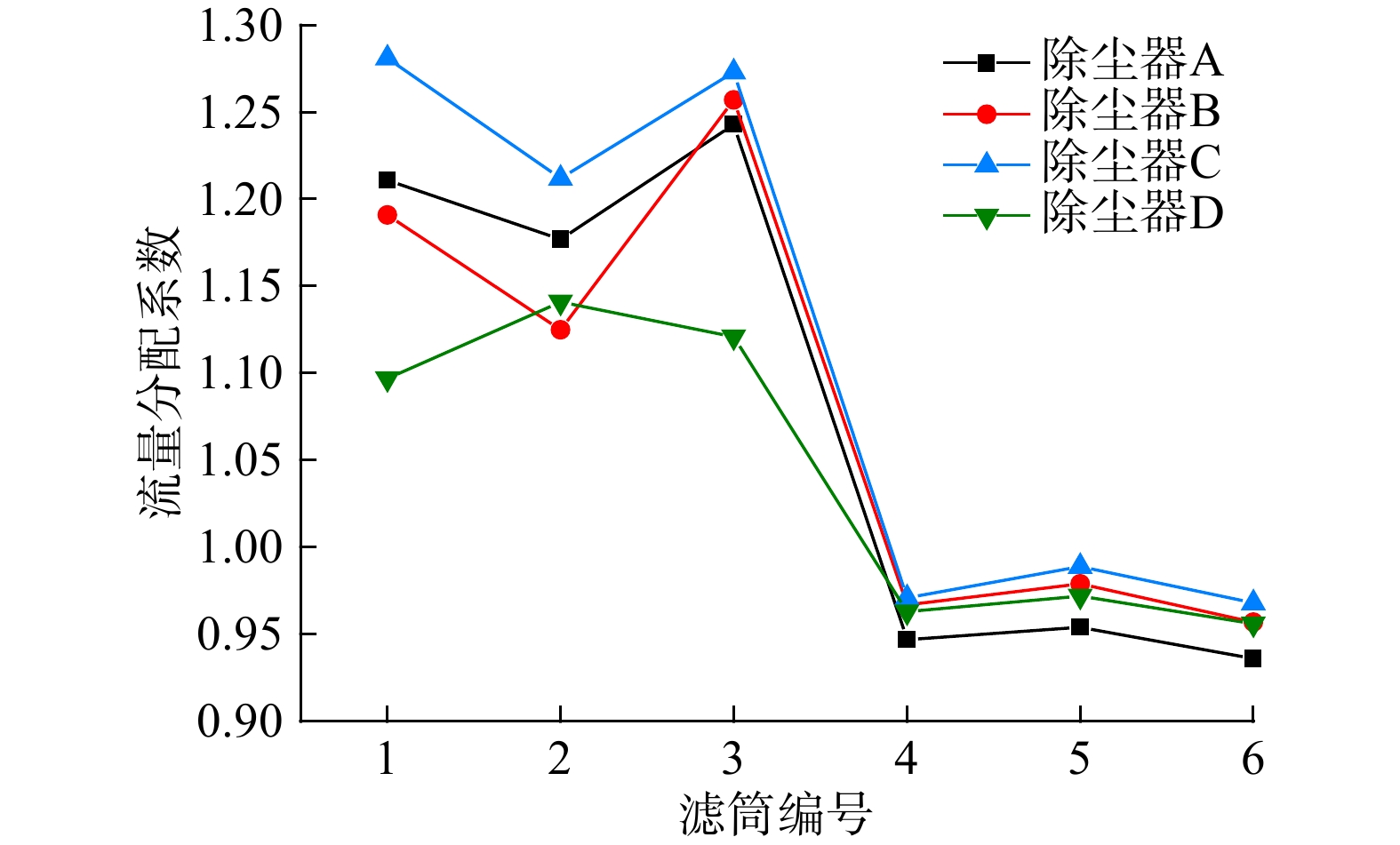
利用Fluent设置监控面,对滤筒流量进行了统计。除尘器滤筒流量分配不均匀,会使滤筒处理气量达不到设计值。因此,研究除尘器各滤筒流量均匀性对除尘器高效运行具有重要意义[14]。为更好地定量分析除尘器流场分布状态,引入流量分配系数Ki、流量分配差值ΔK、综合流量不均幅值ΔKζ,分别对应方程式(6)~(8)。
Ki=QiQm(i=1,2,3,⋯,n) (6) ΔK=Kimax−Kimin (7) ΔKζ=∑(|Ki−1|N) (8) 式中:Qi 为单滤筒实际处理气量,m3·s−1;Qm 为滤筒平均处理气量,m3·s−1;n是模型中所选取的滤筒总数[15]。Ki max,Ki min 分别为单滤筒最大及最小流量分配系数。其中,Ki 一般在1.0左右浮动;在实际工况中ΔK ≠0,一般ΔK 为±15%之内。ΔK 越趋向0,代表各滤筒过滤越平均效果越好,可默认各滤筒气量均匀分配[16]。而综合流量不均幅值ΔKζ 是指实际流量分配系数与理想流量分配系数的平均值。此参数综合考虑了各个滤筒的流量偏差[15],评价比较全面。综上所述,对于滤筒处理气量,要使Ki趋向1.0,ΔK趋向0。
图7为除尘器A、B、C、D各滤筒的流量分配系数Ki。图7表明,除尘器D各滤筒流量分配最为均匀,上下滤筒处理风量差异较小,流量分配系数Ki 基本在1.0附近波动。由表1可知,除尘器D滤筒在导流板和分离式挡板γ作用下,流量分配差值ΔK 仅为18.5%,综合流量不均幅值ΔKζ 为7.7%,最大正负偏差变化也最小,故可默认在该模型下滤筒气流分配均匀。除尘器A与除尘器C的流量分配系数Ki 总体趋势是一致的,但上层滤筒处理风量明显高于下层滤筒,流量分配差值ΔK均超过±15%,分别为32.7%与33.3%。由此可知,在除尘器A、C中,各滤筒并未充分发挥作用,这不符合滤筒气量均匀分配的标准。此外,上层滤筒流量较大,会加大滤筒的负荷,影响除尘器使用寿命。图7还表明,除尘器B中2号滤筒处理气量明显小于1号、3号滤筒。这是由于受挡板α的影响,气流冲击挡板后方向发生改变,导致1号、3号滤筒外侧气流速度较高,而2号滤筒处于挡板正下方,处理气量明显偏少。综合分析滤筒表面速度云图和各滤筒流量分配情况后发现,滤筒表面风速对其流量分配系数影响较大[6]。在合理条件下,通常滤筒表面风速越低、变化越小,则各滤筒间流量越均匀,更有利于发挥滤筒的过滤功能。
表 1 除尘器流量分配结果Table 1. Flow distributions of the dust collector除尘器种类 流量分配差值 最大正偏差 最大负偏差 综合流量不均幅值 除尘器A 32.7% 16.5% −14.2% 13.3% 除尘器B 30.0% 18.5% −11.5% 10.6% 除尘器C 33.3% 16.5% −14.8% 14.2% 除尘器D 18.5% 9.9% −8.6% 7.7% 2.4 除尘器的压降问题分析
除尘器的压降由多种因素导致,而压力损失是衡量除尘器运行成本的关键因素。压力损失大表明除尘器运行成本高,且影响除尘器的清灰周期及设备寿命。在入口管道处添加导流板和挡板后会使除尘器内部结构发生改变,相应的局部阻力也发生变化。这是因为边界改变区域会出现漩涡区和速度重新分布,使得局部阻力增大。同时,这些结构会加大流体之间,以及流体与除尘器之间的接触,使得摩擦阻力增加[17]。通常情况下,局部阻力影响较大。
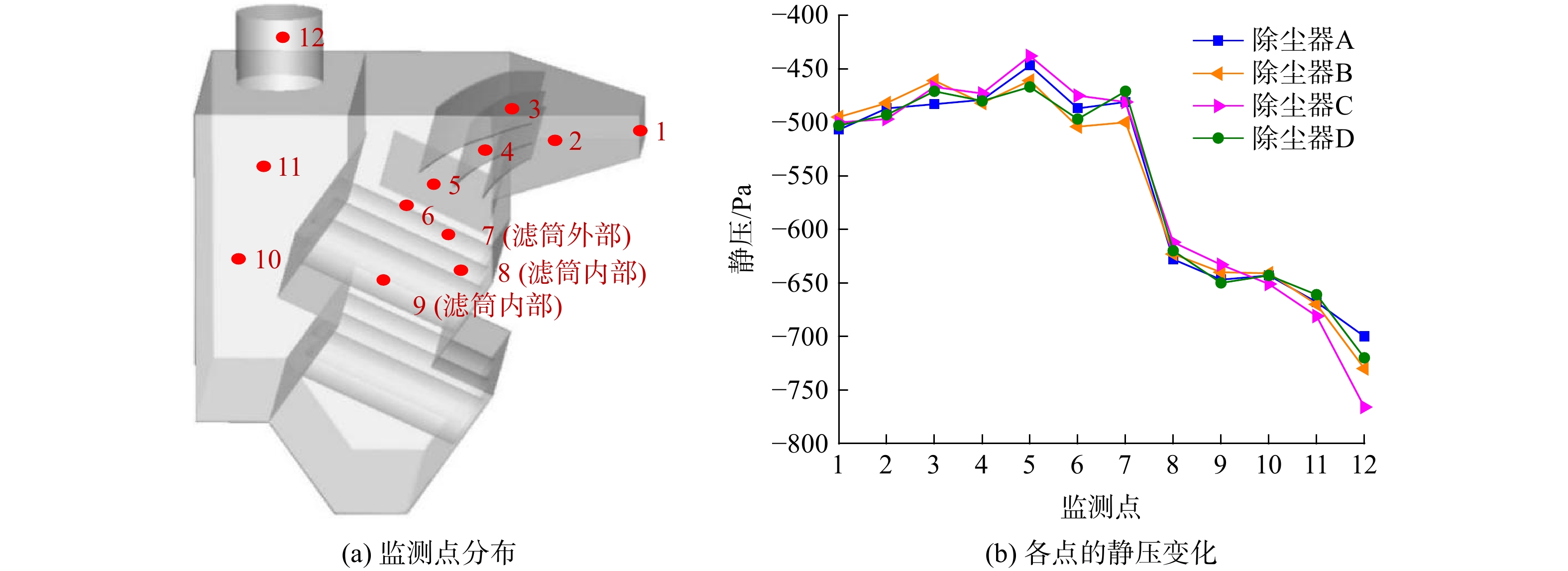
当风速一定时,除尘器的静压主要由其内部结构决定[18-20],可分析静压以较好地说明压降的状况。本除尘器为负压系统。以除尘器B为例,在入口、进风管道、导流板、挡板、滤筒、出口等位置设置12个有代表性的静压测点(见图8(a))。图8(b)为除尘器A、B、C、D分别在这些监测点的压力变化趋势。由图8(b)可知,4种除尘器压降变化趋势一致。除尘器A作为常规卧式滤筒除尘器,其压降变化最小;除尘器B、C、D在加入导流板和各种挡板后运行阻力增加,但变化幅度都较小。这说明添加导流板与挡板α、β、γ后,除尘器静压损失方面控制较好,并未使运行成本大幅增加,符合节能环保的要求。其中,安装了分离式挡板γ的除尘器D压力损失表现最好。
3. 结论及建议
1)运用Fluent等软件对常见的侧进气卧式滤筒除尘器进行CFD模拟,发现传统的卧式滤筒除尘器内部流场较为紊乱,易造成二次扬尘问题,滤筒气量分配不均,局部滤筒过早出现破损,可导致除尘器寿命衰减。
2)对卧式滤筒除尘器内部进行优化,在入口添加导流板及不同类型的挡板,综合分析内部流场、滤筒表面风速、除尘器压降、滤筒流量分配均匀性等因素后可看出,添加了导流板与分离式挡板γ的除尘器D的除尘效果最优。
3)除尘器内部结构对其流场状态起决定性作用。预先对除尘器进行气流组织模拟,得到最优的结构参数,可指导现实的工程设计。后续研究可重点关注模拟和实验测试的过滤效率及能耗等。
-
[1] 张强. 大气边界层气象学研究综述[J]. 干旱气象, 2003, 21(3): 74 − 78. [2] LIU S Y, LIANG X ZH. Observed diurnal cycle climatology of planetary boundary layer height[J].Journal of Climate, 2010, 23: 5790-5809. [3] 魏浩, 胡明宝, 艾未华. 小波变换在风廓线雷达探测大气边界层高度中的应用研究[J]. 热带气象学报, 2015, 31(6): 811 − 820. [4] 王琳, 谢晨波, 韩永, 等. 测量大气边界层高度的激光雷达数据反演方法研究[J]. 大气与环境光学学报, 2012, 7(4): 241 − 247. doi: 10.3969/j.issn.1673-6141.2012.04.001 [5] 王珍珠, 李炬, 钟志庆, 等. 激光雷达探测北京城区夏季大气边界层[J]. 应用光学, 2008, 29(1): 96 − 100. doi: 10.3969/j.issn.1002-2082.2008.01.023 [6] 沈建, 沈利洪, 韩笑, 等. 激光雷达与微波辐射计联合观测大气边界层高度变化[J]. 气象科技, 2017, 45(3): 425 − 429. [7] 李红, 马媛媛, 杨毅. 基于激光雷达资料的小波变换法反演边界层高度的方法[J]. 干旱气象, 2015, 33(1): 78 − 88. [8] LEWEIS J R. WELTON E J, MOLOD A M. Welton, REA M . Molod. Improved boundary layer depth retrievals from MPLNET[J]. Journal of Geophys. Reseach, 118,6: 1-10 [9] 刘辉志, 冯健武, 王雷, 等. 大气边界层物理研究进展[J]. 大气科学, 2013, 37(2): 467 − 467. doi: 10.3878/j.issn.1006-9895.2012.12315 [10] 刘思波, 何文英, 刘红燕, 等. 地基微波辐射计探测大气边界层高度方法[J]. 应用气象学报, 2015, 26(5): 626 − 635. doi: 10.11898/1001-7313.20150512 [11] 滕继峣, 秦凯, 汪云甲, 等. 基于激光雷达观测的大气边界层自动识别局部最优点算法[J]. 光谱学与光谱分析, 2017, 37: 361 − 367. [12] 杨富燕, 张宁, 朱莲芳, 等. 基于激光雷达和微波辐射计观测确定混合层高度方法的比较[J]. 高原气象, 2016, 35(4): 1102 − 1111. [13] 狄慧鸽, 候晓龙, 赵虎, 等. 多波长激光雷达探测多种天气气溶胶光学特性与分析[J]. 物理学报, 2014, 63(24): 244206. doi: 10.7498/aps.63.244206 [14] 张婉春, 张莹, 吕阳, 等. 利用激光雷达探测灰霾天气大气边界层高度[J]. 遥感学报, 2013, 17(4): 981 − 992. [15] 卜令兵, 袁静, 高爱臻, 等. 基于激光云高仪的雾霾过程探测[J]. 光子学报, 2014, 43(9): 09010021 − 09010026. [16] 陈臻懿, 刘文清, 张玉钧, 等. 用激光云高仪测量边界层高度[J]. 激光技术, 2009, 33(5): 455 − 458. doi: 10.3969/j.issn.1001-3806.2009.05.003 [17] ZHU X W, TANG G Q, GUO J P. Mixing layer height on the North China Plain and meteorologicalevidence of serious air pollution in southern Hebei[J]. Atmospheric Research, 2018, 209: 204 − 211. doi: 10.1016/j.atmosres.2018.03.019 -






 下载:
下载: