-
随着产业升级和城市扩张，大量工厂搬迁或废弃后遗留的场地存在土壤污染问题，需要进行土壤修复才能再次开发[1]。电阻加热技术具有对环境扰动小，受土壤异质性影响小，处理深度大等优点，尤其适合修复含有挥发性、半挥发性有机污染物的污染场地[2-5]。但在实际修复工程中，ERH技术的工程参数设计，例如电极间距、电场强度等，都会显著地影响场地电阻加热的实际效果[6]，导致修复周期和成本控制的不确定性。修复场地的污染物分布、地下水流场和土壤特性等往往差异较大，但工程师只能根据已有工程经验和有限的取样勘探结果，进行原位加热工程的参数设计。若能够采用建模的方法，对场地条件下的加热过程进行预测，将有利于减少设计的盲目性，帮助缩短工程周期和控制修复成本。
目前，对于ERH技术的数值模型已经有了一定的探索和应用。HIEBERT等[7-8]开发了用于模拟单相电阻加热过程的二维有限差分模型，并研究了不同的横卧电极设置方式对非均质含油地层的加热效果的影响。CARRIGAN等[9]将改进的欧姆加热模型与非等温多孔流动和传输模型进行了耦合，研究了电极阵列的电相位如何影响电阻加热的均匀性。MCGEE等[10]进一步简化了模拟多相电阻加热的欧姆方程，并模拟了电阻加热从非均质油砂中回收沥青的过程。KROL等[11]考虑温度对密度、粘度、扩散系数的影响，建立了二维有限差分模型，模拟了电阻加热到50 ℃的情况下对地下水流动的影响，发现地下水流动方向和流速发生显著变化。许丹芸等[12]使用有限元方法模拟了电阻加热土壤过程。
尽管关于ERH技术的数值模型研究已有一定的开展，但一方面，以往的模型对电阻加热土壤过程中的水分蒸发缺乏关注和进一步的验证；另一方面，大部分模型是针对实际场地的验证评估，对如何运用模型指导ERH工艺参数的选取探讨不足。本研究使用COMSOL多物理场耦合软件，基于有限元计算方法开展原位电阻加热温度场模拟研究，建立了考虑土壤水分蒸发的模拟原位电阻加热温度场的数值模型。通过对比土柱装置小试实验和数值模拟的结果，验证了数值模型的准确性，并利用数值模型分析了场地尺度下电场强度、电极间距和地下水流动对电阻加热温度场的影响。本研究结果有助于预测修复周期和优化电极井布设，从而达到节约能源和降低修复成本的目的。
-
本研究利用COMSOL的传热模块、电流模块、PDE模块以及电流和传热耦合的电磁热模块，构建土壤电阻加热模型。为简化模型概念，在模拟时做如下假设：1)忽略土壤和水在加热过程中密度、热容随温度的变化；2)将土体视为均质且各向同性的多孔介质，土壤初始温度均匀一致；3)忽略土体在加热过程中的热变形；4)忽略电极和土壤之间的接触电阻；5)由于实验土柱较短，需要考虑水分在低于沸点时的挥发[13]，但在模拟大尺度的场地加热中，忽略水分的挥发；6)忽略水蒸气对热量传递的影响。
电阻加热土壤过程中能量的控制方程如式(1)所示。
式中：ρeff为单元的有效密度，kg·m−3；Ceff为单元的有效热容，J·(kg·K)−1；T为温度，K；t为时间，s；λ为导热系数，W·(m·K)−1；σ为土壤电导率，S·m−1；E为电势梯度，V·m−1；mLG为水的气化速率，kg·(m³·s)−1；ΔHvap为水的潜热，J·kg−1；ρf为流体密度，kg·m−3；Cf为流体热容，J·(kg·K)−1；uf为流体流速，m·s−1。
土壤单元的有效密度ρeff和有效热容Ceff由土壤中固，液，气三相的体积分数决定，如式(2)~式(3)所示。
式中：θ表示各相的体积分数；ρ为各相的密度，kg·m−3；C为各相的热容，J·(kg·K)−1；下标S，L，G表示固，液，气三相。
土壤含水量的控制方程如式(5)所示。
式中：DL为导水系数，m2·s−1；α为比例常数，m2·s−1；θL*为残余饱和度。
液态水变为气态水的情况可分为2种，一种是低于水的沸点时的挥发，一种是到达沸点时的沸腾，用式(6)可以得到水的气化速率。需要注意，只有水的饱和蒸气压(p*)大于等于外部气压(pG)且含水量大于0时，沸腾才会发生。可以通过安托因方程[14](式(7))计算不同温度下水的饱和蒸气压，进而判断温度是否到达沸点。
式中：A、B、C为经验常数；mvap为挥发速率，kg·(m³·s)−1；kvap为蒸发速率常数，s−1。
土壤单元的热导率会随着温度和含水量的变化发生极大的变化，在此使用TARNAWSKI等[15]推导出的经验公式，如式(8)~式(9)所示。
式中:下标sat和dry分别表示饱和和干燥状态的土壤；a~g为经验常数；Sw为水饱和度。
电阻加热一般使用低频率电压(50~60 Hz)，产生的电磁波长远大于系统的物理尺寸，位移电流可以忽略，因此可以假设电阻加热产生的电场为准静态电场，可以通过将欧姆定律代入电流连续性方程中来求解电势分布，电流连续性方程如公式(10)所示。
土壤电导率则使用Archie定律进行计算[16-17]，考虑温度对电导率的影响[18]，如式(11)所示。
式中: ψ为电势，V；φ为孔隙度；m、n和β为经验常数(m为胶结系数，n为饱和度系数，β为温度系数)；σL为土壤溶液电导率，S·m−1。
模拟单相交流电加热时，其电势分布与直流电基本一致，可以设置2个电极分别为接地和施加的电压。但模拟三相交流电时，电极电势与直流电则完全不同，三相交流电的电极电势可以视为由虚部和实部组成[19]，如式(12)所示。
式中：ω为角频率，rad·s−1；t为时间，s；θ为相角，°(三相交流电分别为0 °、120 °和240 °)；j为虚部；E0为正弦交流电振幅的绝对值，一般为电压的21/2倍，V。
-
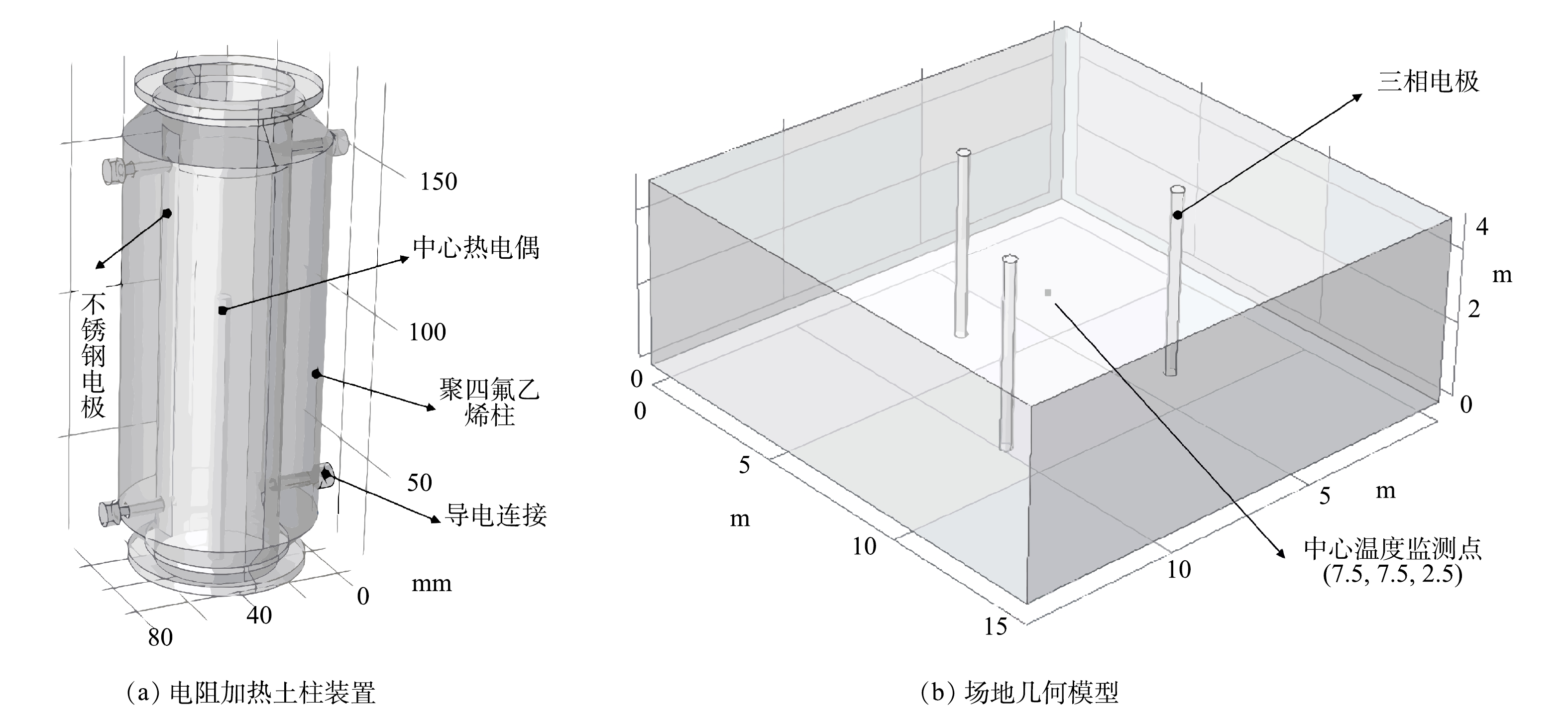
电阻加热土柱装置模型如图1(a)所示，装置高16 cm，内径4.5 cm。装置的罐体用不导电的聚四氟乙烯制成，内部装填细砂。装置2边为对称分布的用螺丝与螺母固定的不锈钢片电极，螺丝作为导电连接，电线连接到螺丝上以引入电压，热电偶从装置底部插入，用于监测土柱中心点的温度。使用Solidworks对电阻加热土柱装置进行建模，得到电阻加热土柱装置的几何模型，再导入到COMSOL中用于模拟，几何模型的网格划分均采用三角单元网格，单元大小选择细化。
为了模拟实际场地中电阻加热的过程，构建了图1(b)所示的三相电阻加热场地模型。场地模型为长宽15 m、高5 m的长方体，在场地中部按等边三角形放置3根半径20 cm、高5 m的电极，电极间距为6 m，并在3个电极构成的等边三角形中心点设置了温度监测点。
-
电阻加热土柱装置数值模拟的边界条件为：1)流动边界条件，所有边界均设置为0通量边界条件，这是因为已在方程中添加了描述水蒸发的汇项；2)温度边界条件，所有边界均设置为自然对流热通量边界；3)电势边界条件，2个电极分别设置为接地和电势，其他边界设置为电绝缘边界。土壤的初始温度、含水量、水的电导率和电极电压根据实测得到的初始值设置。对于各项参数的取值如表1所示。
电阻加热场地模拟的边界条件为：1)流动边界条件，模拟地下水位上涨时，底部边界设置为通量边界条件，其他边界设置为0通量边界条件；2)温度边界条件，地下水流入的边界设置为流入边界，流入温度10 ℃，其他边界设置为热绝缘边界；3)电势边界条件，3个电极分别设置为三相电势中的1相，其他边界设置为电绝缘边界。各项参数的设置与土柱装置实验相同。
-
为验证模型在不同的土壤含水量和土壤溶液电导率时的准确性，使用电阻加热土柱装置进行了验证实验。由于装置较小，电场强度较大，故使用电导率较小的细砂充当模拟土壤。分别向300 g细砂中加入40、50、60、70 mL的去离子水，质量分数为0.3%的NaCl溶液和质量分数为0.5%的NaCl溶液，充分搅拌，并装填进装置中。为了保持砂的孔隙度一致，在装填时保证装填高度为15 cm。加入去离子水的砂在100 V的条件下进行电阻加热，加入NaCl溶液的砂在50 V的条件下进行电阻加热。由于模拟只探究电阻加热的升温过程，所以实验只进行到温度到达100 ℃就停止，未加热到100 ℃时则在加热2 h后停止。
为模拟实际工程环境下土壤内热量传递规律，用实际场地模型探究了地下水流动、电场强度和电极间距的变化对土壤温度变化的影响。模拟的工况如表2所示，其他参数与表1一致，土壤溶液电导率设为0.1 dS·m−1。
-
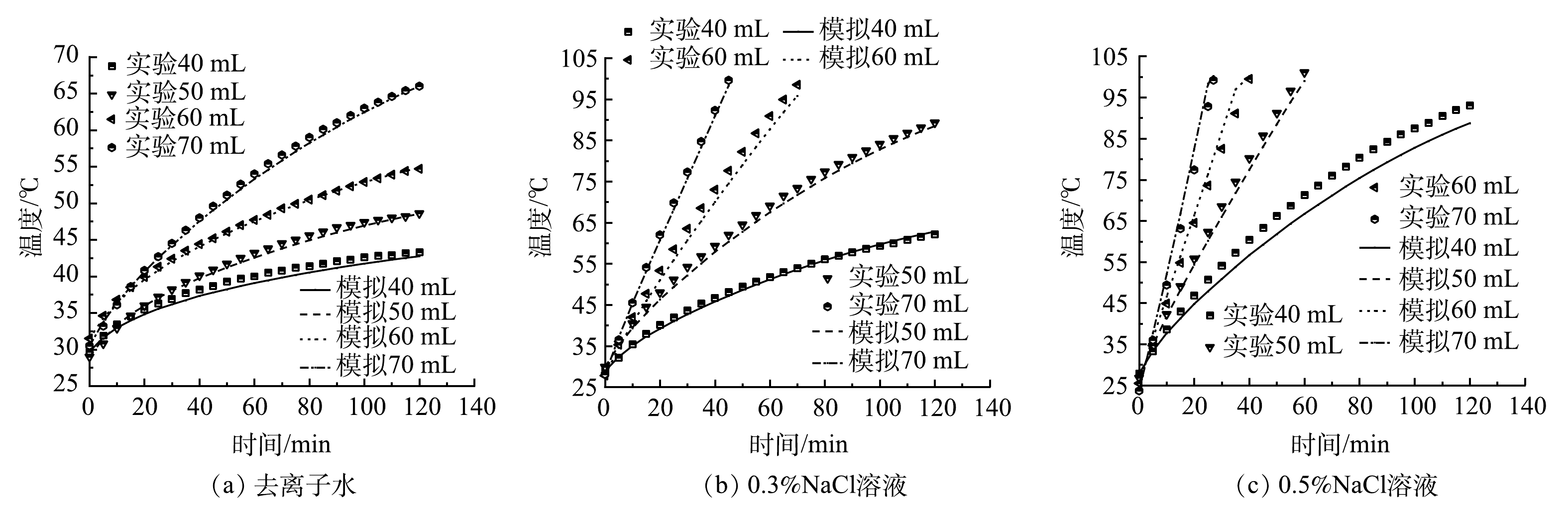
图2给出了不同含水率和电导率的情况下，土柱中心热电偶监测的温度变化。可以看出，随着含水量和土壤溶液电导率的增加，中心点加热到100 ℃所需要的时间不断减小。而当含水量较小或者土壤溶液电导率较小时，升温速率较小，甚至出现温度平台的情况。升温速率较小是由于此时土壤电导率较小[20]，电流产生的焦耳热较小。升温速率减小则是因为，土柱中挥发掉的水份随着加热时间的增长逐渐变多[21]，进一步降低了土壤电导率，使电流产生的焦耳热进一步减少。此外，由图2(a)可以看到，加入不同体积的去离子水后的细砂依然可以被加热，而去离子水的电导率几乎可以忽略不计。这说明，细砂中的离子溶解进入了去离子水中，提高了去离子水的电导率。
为验证模型的可靠性，将不同含水量和土壤溶液电导率的电阻加热实测值和模拟值进行了对比。利用均方误差MSE和平均相对误差MRE评价模拟值和实测值的差异(式(12)~式(13))。
式中：n为实测数据个数；Mi、Si分别为第i个实测和模拟得到的数据。
图2(a)中给出的模拟值趋势线与实测值差异较小，实测值和模拟值均方误差为0.05~0.66，平均相对误差为0.42%~1.97%。较小的均方误差和平均相对误差表明，实测数据与模拟数据之间的偏差较小，模型具有较好的准确性。加入不同体积的0.3%NaCl(图2(b))和0.5%NaCl(图2(c))溶液，土壤溶液电导率随着NaCl溶液的体积和质量分数的增加而增大。对比实测和模拟预测结果，均方误差为0.38~12.29，平均相对误差为1.15%~5.32%。这表明，在较宽的土壤电导率范围内(加入70 mL的0.5%NaCl溶液时，土壤的电导率为1.1 dS·m−1)，实测数据与模拟数据之间的偏差也较小，模型用于预测不同电导率的土壤加热过程是可靠的。误差产生的原因可能是，对土壤原有的电导率，实验过程中空气热对流导致的热量散失以及水分挥发速率的估值存在一定的偏差。
-
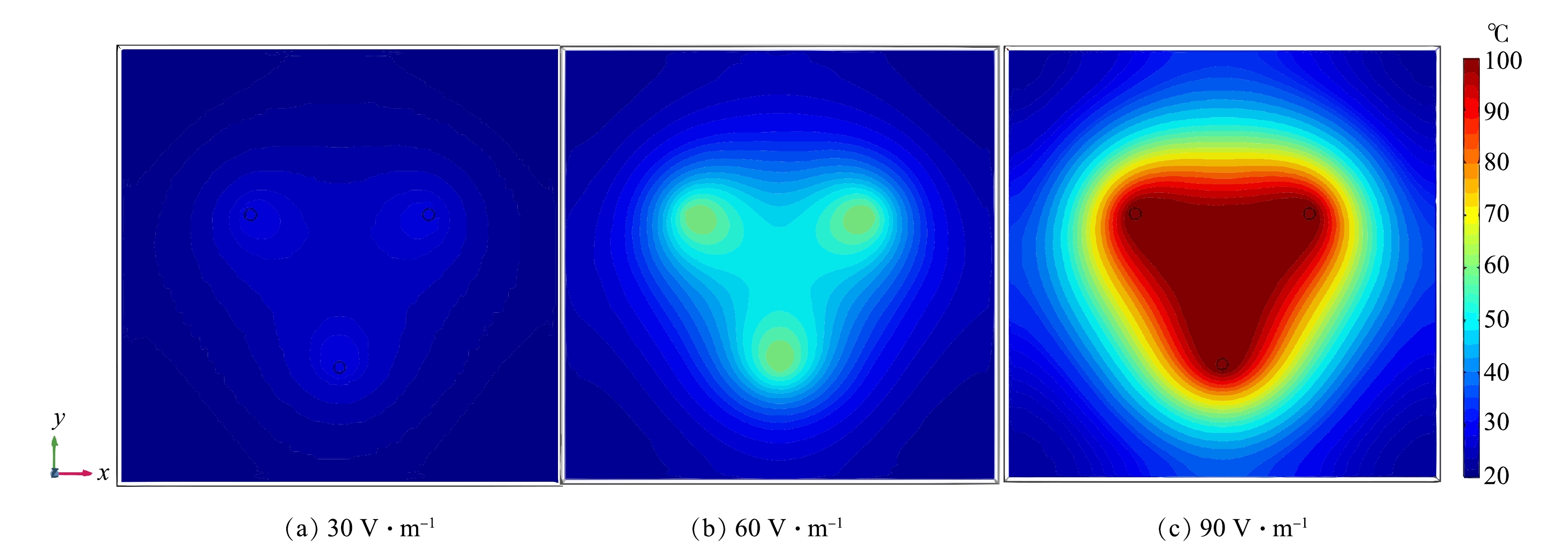
电场强度是影响电阻加热升温速率的重要因素，由电极电压和电极间距共同决定，为了考察场地尺度下的温度场以及各条件对温度场的影响，建立了图1(b)的场地模型。图3和图4分别展示了电极间距6 m时，30、60、90 V·m−1电场强度下加热70 d后，温度场的横截面以及位于3个电极中心点(见图1(b))温度的变化。从图3可以看出，电场强度越大，土壤升温速率越快，电极附近的升温更快，温度更高。这与MCGEE等[10]和HAN等[22]的研究结果是一致的。电流产生的焦耳热随电场强度的增大而增大，电场强度越大，土壤升温速率越快；电极附近的电流密度最高，产生的焦耳热最多，所以土壤升温速率更快。
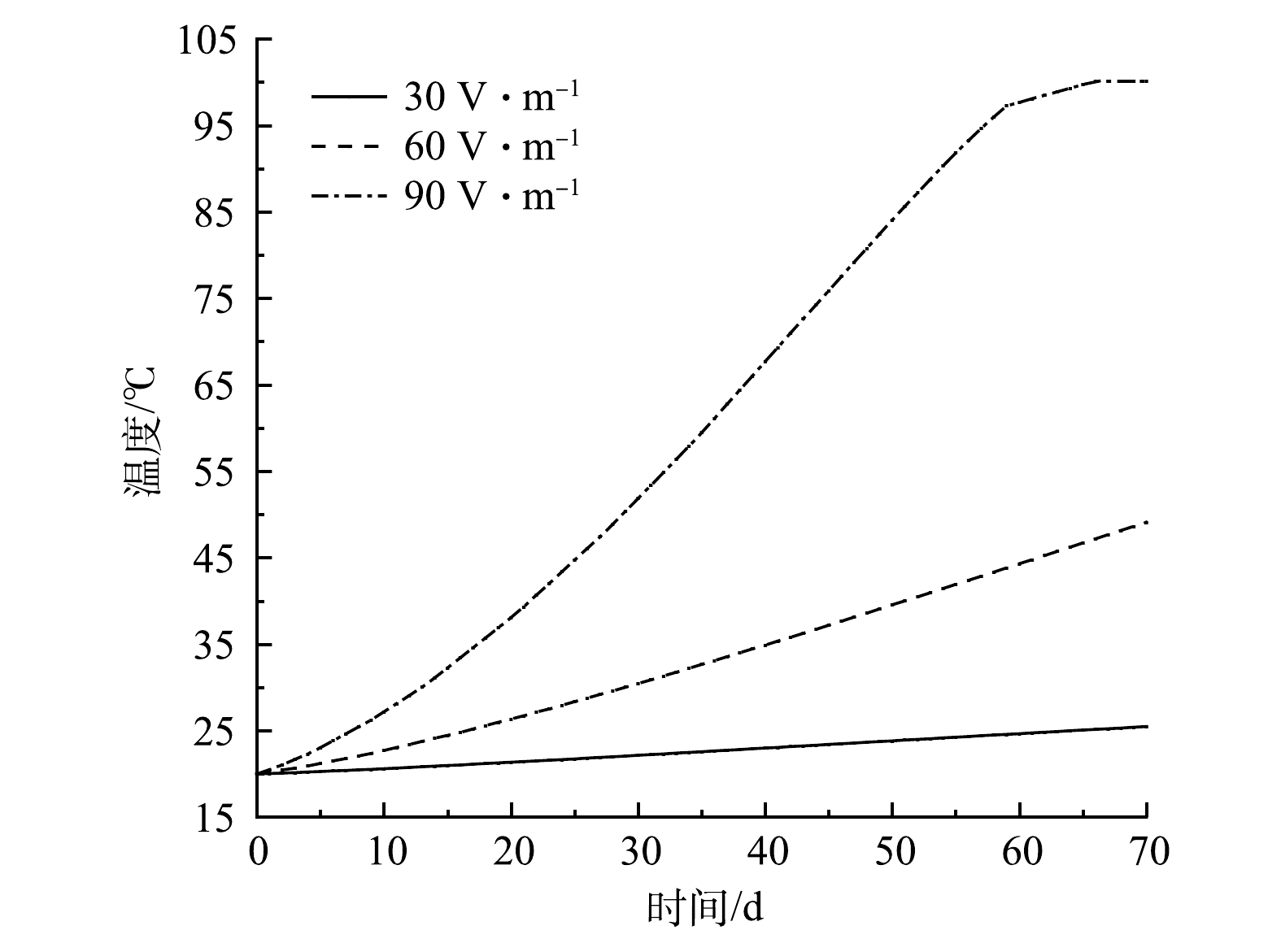
从图4可以看到，场地在加热90 d后，30、60和90 V·m−1电场强度获得的中心温度分别为25.5、49.1和100.0 ℃，中心点的平均升温速率分别为0.079，0.420和1.210 ℃·d−1。由式(1)可知，焦耳热与电场强度的平方呈正比，电场强度为30、60、90 V·m−1时中心点升温速率之比应为1∶4∶9，小于模拟得到的比值，即1∶5.3∶15.5。这说明，中心点的温度可能是电流焦耳热和外部热传导叠加共同决定。此外，电场强度为90 V·m−1时，当中心点温度达到97 ℃后，升温速率明显放缓。这是因为，此时的电极温度已经达到水的沸点，电极土壤水分蒸发带走了大量热量，导致土壤热导率和土壤电导率下降，从而使升温速率下降。
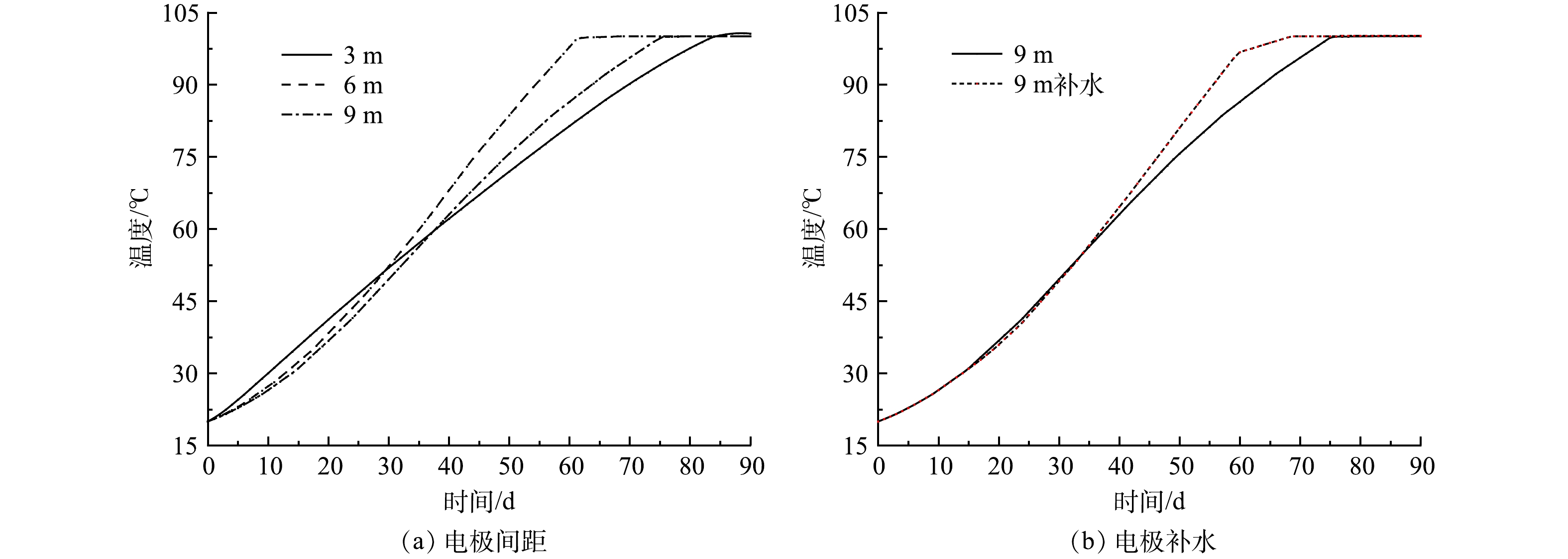
电极间距的设置决定了电极井的数量，会极大地影响修复场地的成本和热传导过程。为探究电极间距这一单因素对电阻加热过程的影响，在保持电场强度90 V·m−1不变的条件下，模拟电极间距3、6和9 m时中心温度的变化，结果如图5所示。从图5(a)可以看出,在电场强度为90 V·m−1，电极间距为3、6和9 m时，中心点的温度达到100 ℃的时间分别为84、62和75 d，达到100 ℃的能耗分别为10 418、23 375和51 311 kW·h。综上可知，6 m为最适宜的电极间距，此时中心点的升温速率最快，且相较于电极间距为3 m时场地修复需要布设的电极井数量更少，相较于电极间距为9 m时需要的能耗更少。从图5(a)还可以看出，随着电极间距的增大，中心点升温速率先增大后减小。这是因为，为了保证电场强度一定，电压随电极间距增大而增大，导致电极处的升温速率也随之增大，这一定程度上弥补了间距增大导致的中心点热传导距离增大的不足。但是，9 m间距下的电压增加，造成电极附近温度过早达到水的沸点，导致电极周围土壤水分过早蒸发，土壤热导率和电导率下降，升温速率略为下降。
为了考察电极附近土壤水分蒸发对中心点升温速率的影响，模拟了电场强度90 V·m−1、电极间距为9 m时，对电极附近补水的情况下，中心点温度的变化。从图5(b)可以看到，在加热40 d后，补水的情况下中心点温度明显高于不补水的情况，补水的情况下中心点的温度达到100 ℃的时间为68 d，比不补水的情况下早8 d。此结果表明，电极周围土壤水分过早蒸发是造成升温速率下降的原因之一，补水可以使土壤含水率增大，增加土壤的电导率和热导率，提高了升温速率。这与葛松等[3]的研究结果一致。监测电极的电流变化，并及时对电极附近进行补水，对于更快加热到目标温度至关重要。
-
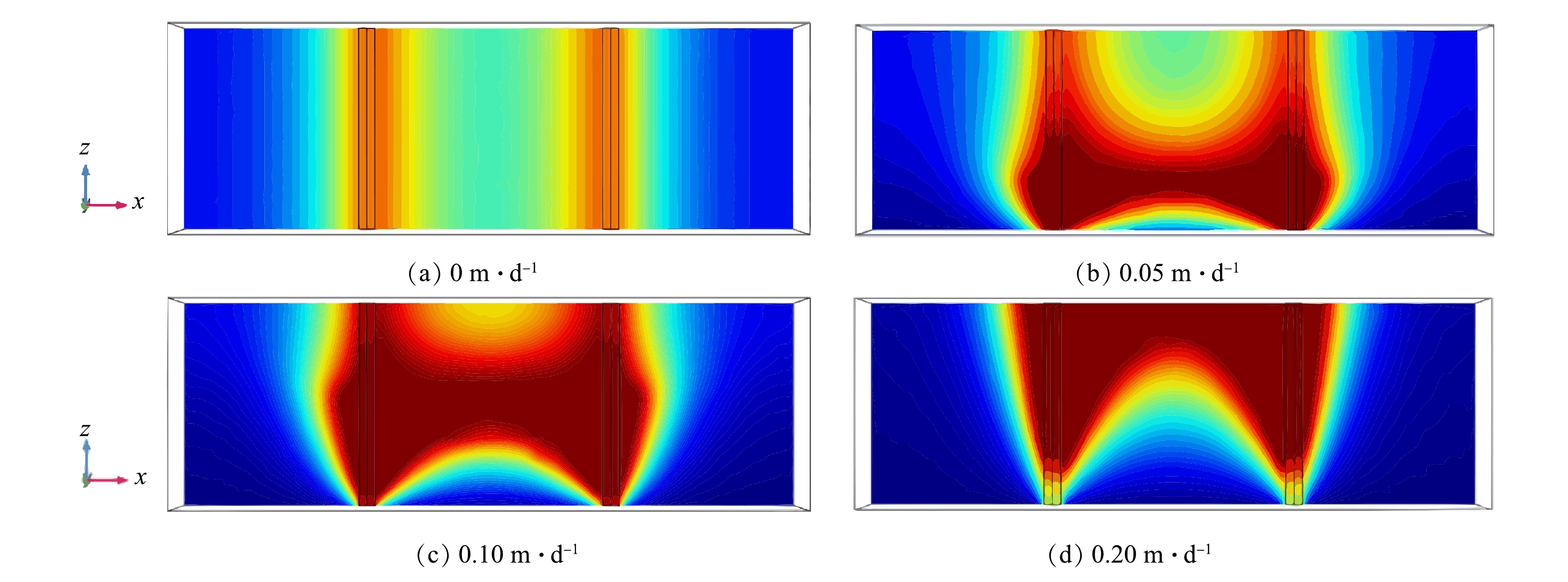
使用原位电阻加热的场地一般修复深度都较大，有必要考虑地下水流动和地下水位变化对温度场的影响。为进行预测，分别设定了0、0.1、0.2、0.3 m·d−1的地下水流速下加热30 d和0、0.05、0.10、0.20 m·d−1的地下水上涨速度下加热30 d的条件进行模拟，流入的地下水出的温度假定为10 ℃，温度场的变化结果如图6和图7所示。从图6可以看到，随着地下水流速的增加，场地左侧的温度逐渐降低到10 ℃，温度场右移的趋势越明显，中心点的最高温度从100.0 ℃降低到38.5 ℃。这说明，较高的地下水流速会将场地中的热量带向下游，对场地升温速率造成不利影响，与MUNHOLLAND等[23]在二维沙箱中得到的结果一致。实际工程中应尽量减小地下水流速，必要时可增加侧向的物理屏障来形成止水帷幕，或通过蒸汽注入等手段来增加流入地下水的温度。
从图7可以看到，随着地下水位上涨速度提升至0.1 m·d−1，场地下部和两侧的温度逐渐降低到10 ℃，但由不饱和区域变为饱和区域的土壤升温速率上升，中心点最高温度从51 ℃升高到100 ℃。随着地下水位上升速度达到0.2 m·d−1，相较于0.1 m·d−1时，温度场明显向上移动，中心点最高温度从100 ℃降低到54 ℃。这是因为，地下水位上涨可以起到一定的补水作用，提高不饱和区域土壤的电导率，从而提高土壤升温速率，但地下水上涨速度过快还是会导致流失的热量多于通过补水增加的焦耳热，使得场地温度从底部开始下降，不利于场地的修复。应当指出，由于实际场地地层的复杂性，地下水的流速和流向并不是均匀的。因此，对于非均质地层，可以建立相应的多模块的空间耦合模型，通过改变各地层模块的物理参数，从而实现数值模拟目标。
-
1)电阻加热温度场数值模型与土柱装置实验数据吻合度较好，模拟值和实测值均方误差为0.05~12.29，平均相对误差为0.42%~5.32%，数值模型具有较好的预测准确性。
2)场地模型研究发现，升温速率与电场强度成正比，电极处升温速率最快；电场强度为90 V·m−1时6 m为最适宜的电极间距，此时中心点升温速率最快，能耗相对较低，需要的电极井较少；模型考虑水分蒸发的情况下，电极周围土壤水分会更早蒸发，导致土壤升温速率下降，此时对电极附近补水可以显著增加土壤升温速率，故在实际工程中应监测电流和功率，并及时对电极附近进行补水。
3)场地地下水流动会带走热量，不利于场地的热修复。但对于不饱和场地，地下水位上涨速度小于等于0.1 m·d−1时可以起到补水作用，提高场地升温速率。故对于地下水流速过高的场地应采取水力平衡或设置止水帷幕等工程措施以缓解热量流失。
原位电阻加热修复热传递模型构建及数值模拟
Modeling of the heat transfer of in-situ electrical resistance heating remediation and numerical simulation
-
摘要: 原位电阻加热(Electrical resistance heating，ERH)技术在场地修复中工艺参数的选取较多依赖于工程经验，ERH热量传递的数值模型能够模拟不同工艺参数下土壤加热的温度场，从而为ERH工艺参数的选取提供理论指导。利用电阻加热土柱装置实验验证了建立的数值模型的准确性，并应用在场地尺度下探讨了电场强度、电极间距和地下水流动对原位三相电阻加热的影响。结果表明，模型具有较好的准确性，实测值和模拟值均方误差为0.05~12.29，平均相对误差为0.42%~5.32%。随着电场强度越大，土壤升温速率显著加快；电场强度90 V·m−1时，综合考虑电极井建设数量、加热时长及能耗，最适宜的电极间距为6 m；对电极附近补水可以显著缩短加热时长。较快的地下水流动会降低场地升温速率，不利于场地的修复；对于地下水流速过快的场地应采取适当的工程措施缓解热量流失。本研究结果可为原位电阻加热工程的设计和运行提供参考。Abstract: The selection of process parameters of in-situ electrical resistance heating (ERH) technology in site restoration is still lack of scientific theoretical guidance. A numerical model of ERH heat transfer was established to simulate the soil temperature field with different operation parameters, so as to provide theoretical guidance for the selection of operation parameters. The accuracy of the model was verified by the ERH experiment using a soil column device, and the effects of electric field intensity, electrode spacing and groundwater flow on the soil temperature field during in-situ three-phase resistance heating were discussed at a site scale. The results showed that the mean square error between measured and simulated values was in the range of 0.05~12.29, and the average relative error ranged from 0.42% to 5.32%, indicating that the model was of good accuracy. With the increase of electric field intensity, the soil heating rate increased significantly. When the electric field strength was 90 V·m−1, considering the number of electrode wells, heating time and energy consumption, the suitable electrode spacing was 6 m. Replenishing water to the heating electrode could significantly shorten the heating time. Rapid groundwater flow reduced the temperature rising rate of the site, which was not conducive to the remediation of the site. Appropriate engineering measures should be taken to alleviate the heat loss in the site with fast groundwater flow rate. This study provides a reference for the design and running of in-situ ERH remediation engineering.
-
随着石油工业、机械加工、食品加工与餐饮业的不断发展，含油废水的排放量日益增大。不经处理的含油废水直接排放会对周边环境造成严重的危害。含油废水中的油可分为浮油、分散油、乳化油和溶解油4种[1]。其中乳化油因其油滴尺寸较小，油水二元体系稳定性强，难以通过重力、气浮等方式实现油水分离，是最难处理的一类含油废水[2]。目前，乳化油废水处理方法包括：膜分离法、吸附法、絮凝法等[3-5]。其中的电絮凝法具有除油能力强、操作简便、自动化程度高、无需添加化学药剂等优点，是一种高效、经济、环保的含油污水处理方法[6]。电絮凝法的缺点在于废水处理过程需要消耗大量电能，导致其水处理成本相对较高。
为了降低废水处理过程的电能消耗，降低废水处理成本。近些年来提出了一种利用工作溶液盐/浓差能驱动的逆电渗析(reverse electrodialysis，RED)技术来处理各种有机/无机废水的技术[7-12]。工作溶液盐/浓差能即可来自于自然界(海水/盐湖水与入海/入盐湖的河水之间的盐差)，也可以来自盐/海水分离副产物(浓盐/海水与自然盐/海水之间的盐差)，还可以通过废热转换(溶液热分离)获得[13]。
1954年PATTLE[14]首次提出利用自然界盐差能的RED发电技术以来，对该技术的研究逐渐深入，各国学者发表了大量有关RED技术的研究论文。RED电堆/反应器的结构和工作原理类似。他们都是由端板、阴/阳电极，交错布置的阴/阳离子交换膜(AEM/CEM)及隔垫所构成。当浓/稀盐溶液分别流经由膜隔垫所隔两电极会产生得失电子的氧化还原反应。电子通过外部电路从阳极流向阴极，从而在外电路中产生电流。发电用的RED电堆与水处理用的RED反应器不同之处在于：电极液在RED电堆内作可逆的闭式循环，而废水作为电极液流经RED反应器电极流道并因电极的氧化还原反应生成各种反应物来降解废水中的污染物。不同的电极材料和废水成分在RED反应器电极氧化还原反应过程中会生成不同的反应物。理论上而言，若RED反应器阳极选用铁或铝作为牺牲阳极时，RED反应器可以产生电絮凝效果来处理一些难以生化降解的有机或无机废水[15]。
但实际上，因在使用过程中牺牲阳极会被不断消耗而需要定期换新，导致需要不断拆装RED反应器造成使用不便。另外，在处理含油废水过程时电极表面易被油膜污染，减弱含油废水的处理效果。为此，本课题组提出了一种如图1所示的RED电堆与常规电絮凝器耦合的乳化油废水处理系统。该系统由工作溶液的盐差能驱动RED电堆发电，电絮凝器作为负载连接在电堆的外部电路中。由于盐差能驱动的RED电堆属于内生电源。在RED电堆结构参数确定的条件下，其输出电参数(电压与电流)与外部电路负载(电絮凝器)电阻有关。而电极材料、电极间隙、处理时间、阳极钝化、含油废水参数(初始pH、电导率和温度)等变化会影响电絮凝器电阻，进而影响其工作效率。因此，本研究采用单因素法，在RED电堆结构和操作参数不变的条件下，考察电絮凝器电极材料、电极间距、支撑电解质浓度、含油废水初始pH及温度对耦合系统的乳化油废水处理效果的影响。
图 1 逆电渗析电堆与电絮凝器耦合处理乳化油废水实验系统Figure 1. Experimental system of reverse electrodialysis reactor coupled with electrocoagulation for emulsified oil wastewater treatment1. 实验系统与方法
1.1 RED电堆与电絮凝器耦合系统
逆电渗析电堆与电絮凝器耦合系统合处理乳化油废水实验系统流程如图1所示。由图1可见，RED电堆与电絮凝器构成一串联电路。实验所用的RED电堆和电絮凝器均为自制。RED电堆由离子交换膜、丝网隔垫及电极构成，离子交换膜有40张CEM以及41张AEM(最外两侧膜采用AEM)，均购自日本富士公司，型号为type 10，厚度为0.12 mm；丝网隔垫厚度为0.38 mm，孔隙率为80%；2个10 cm×10 cm×1.5 cm的钛镀钌铱板构成电极。电絮凝器由有机玻璃(透明亚克力板)制成，电解槽尺寸为20 cm×10 cm×15 cm。槽内壁设有0.3 cm宽的竖直凹槽，用来放置电极板(10 cm×10 cm×0.3 cm)。凹槽下端距电解槽底面1 cm，电极板实际有效浸没面积为90 cm2。电解槽放置在磁力搅拌器上，转子以400 r·min−1的速度不断搅拌电解槽内的含油废水，以使其保持油水均匀状态。选择这个搅拌速度值，是因为它促进了胶体和不稳定物质之间的相遇，而不会在所使用的实验装置内造成任何可察觉的聚合体破裂[16]。
1.2 工作流程
人工配置浓度分别为0.03 mol·L−1和3 mol·L−1的稀/浓NaCl水溶液作为工作溶液并储存在相应的玻璃瓶内(5和7)。0.1 mol·L−1 的铁氰化钾水溶液作为电极液储存在避光的玻璃瓶(3)内。2台蠕动泵(6和8)泵送稀/浓溶液工作溶液流经RED电堆(11)。在稀/浓溶液盐差的作用下，浓溶液中的盐分跨膜迁移到稀溶液中，使得浓溶液浓度降低，稀溶液浓度升高。流出RED电堆的稀/浓溶液分别储存在其相应的玻璃瓶内(9和10)。一台蠕动泵(4)泵送电极液，并在RED阴/阳极回路内作循环流动，以将电荷快速转移到RED正/负极。RED电堆输出电能驱动电絮凝器工作。RED阴/阳(正/负)极与电絮凝器对应的阳/阴极用铜导线相接，构成外部电路。利用数字万用表(12和13)在线检测RED电堆输出电流和电压。RED电堆的理论开路电压可按能斯特(Nernst)方程(式(1))计算[13]。离子活度系数可用扩展的 Debye-Hückel方程(式(2))表示。
U=(αCEM+αAEM)NmRTzFln(γCSCCSγDSCDS) (1) 式中：U为理论开路电压，V；
α γ γ(x)=exp[−0.51z2√Λ(x)1+(A/305)√Λ(x)] (2) 式中：z为离子化合价；A为有效水合离子半径(
ANa+=450pm，ACl−=300pm Λ 由于流经RED电堆的浓、稀溶液浓度会发生变化，因此RED电堆理论开路电压需按浓、稀溶液平均浓度计算。本次实验固定RED电堆结构和操作参数[浓溶液浓度为3 mol·L−1，稀溶液浓度恒定为0.03 mol·L−1，过膜流速均为0.35 cm·s−1(稀/浓溶液流率均为0.134 4 L·min−1)]不变，计算得理论开路电压为6.335 V。RED电堆输出(端)电压为式(3)计算值，在RED输出电能的驱动下，电絮凝器的阳极和阴极发生的电化学反应如式(4)~式(6)所示
Uo=U−IRi (3) 式中：Ri为RED电堆的内电阻，Ω，其由膜电阻，稀/浓溶液流道电阻和电极液流道及电极电阻所组成。
阳极氧化反应：M=Mn++ne− (4) 阴极还原反应：2H2O+2e−→2OH−+H2↑ (5) 总反应：Mn++nOH−→M(OH)n (6) 反应生成的单体和聚合氢氧化物作为絮凝剂具有高吸附性能，它与废水中分散的颗粒和溶解的污染物具有很强的亲和力。因此，可以通过絮凝作用去除废水中的污染物。絮凝后的产物可以通过漂浮或沉淀的方法从水相中分离出来。阴极还原反应所产生的氢气气泡可促进污染物聚结过程，有助于采用浮选去除乳化油废水中的油组份。氢气泡尺寸越小，絮凝体的截留面积越大，污染物与水的分离效果也越好[17]。此外，电场也被证明是一种有效的破乳方法。在电场力的驱动下，油滴沿着电场的方向运动，然后聚集并破乳[18]。油滴在电场中极化，导致相邻油滴之间的静电吸引力增强[19]。
1.3 材料及仪器
以自制乳化油废水作为研究对象。乳化油制备过程为：每升水中含40 g15#机油(购自德国德殻石化(中国)发展有限公司)并添加8 g十二烷基苯磺酸钠作为稳定剂。采用磁力搅拌器以1 000 r·min−1的速度搅拌30 min，形成稳定的油水乳状液。去除表面浮油后的乳化油再作进一步稀释。稀释后取2 L含油量为1 g·L−1的含油废水进行实验研究。利用氢氧化钠和硫酸来调节含油废水的初始pH，并通过添加支撑电解质(Na2SO4)来调节含油废水的电导率。
实验中各种溶液配制所需的溶剂水为去离子水，所用的盐/电解质购自天津大茂化学试剂厂，为分析纯级，其所含杂质可以忽略。
实验所用的仪器有，紫外可见分光光度计(UV1780，日本岛津有限公司)；蠕动泵(BT100-2J，保定兰格恒流泵有限公司)；蠕动泵(KCP PRO-2-N16，卡默尔流体科技(上海)有限公司)；电子天平(JJ1023BC，G电子秤有限公司)；数字万用表(KEITHLEY 2110-220，美国泰克科技有限公司)；低速离心机(LSC-20，上海秋佐科学有限公司)；热力磁力搅拌器(EMS-9A，天津欧诺仪器股份有限公司)；电导率仪(FE38，梅特勒托利多科技(中国)有限公司)；pH测试仪(PXSJ-226，上海雷磁仪器有限公司)。
1.4 实验和测试方法
每次实验前，铁或铝阳极先要在稀硫酸溶液中浸泡15 min，捞出后用砂纸打磨再用去离子水冲洗，去除表面氧化层。在实验过程中，含油废水处理时长为60 min，每隔10 min抽取电解槽(18)中的水样。对所有水样进行离心处理，将电絮凝过程中形成的絮凝物从水相中分离出来。在每份水样中取1 mL加入氯化钠进行破乳。氯化钠投加量为总体积的5%。然后用10 mL石油醚萃取水样中的油以便测量。测量时通过紫外可见分光光度仪测试水样的吸光度，通过依据绘制的标准曲线反推其浓度。按式(7)计算除油率。为了探索操作参数变化对含油废水处理效果的影响，采用单一变量法进行实验。相同的实验重复2次。
R=(1−Ct/C0)×100% (7) 式中:C0为含油废水中油初始质量浓度，mg·L−1；Ct为絮凝处理t时间后测得含油废水中油质量浓度(乳化后的含油废水紫外光吸收波长峰值λ=225 nm)，mg·L−1。
2. 结果与讨论
2.1 电极材料对极板间电压及除油率的影响
电絮凝器电极选用不锈钢-铁、不锈钢-铝、石墨-铁、石墨-铝、钛镀钌铱-铁、钛镀钌铱-铝6种阴-阳极材料组合，用以考察不同阴-阳材料组合对乳化油废水去除效果的影响。图2给出了不同电极组合下极板间电压及除油率随时间的变化关系。其中，实验条件为：极板间距1 cm、含油废水中添加0.1 mol·L−1硫酸钠，pH为7.8 (pH不为7的原因是配备的乳化油中添加了支撑电解质Na2SO4，SO42-离子可以少量结合H+离子，间接引起pH升高)，温度20 ℃。
图 2 不同电极组合下极板间电压及除油率随反应时间的变化Figure 2. Variation of inter-plate voltage and oil removal rate with time at different electrode combinations由图2(a)可见，采用铝阳极时极板间电压远高于采用铁阳极，而RED的输出电压与电絮凝器采用何种阳极材料关联不大。此外，实验还发现采用铝阳极时串联电路的电流远低于采用铁阳极时的电流，因此，虽然采用铝阳极时极板间电压较高，但采用铁阳极絮凝时，RED电堆可以输出更大的电流。
根据法拉第电解定律，通过的总电荷越多，电极产生的混凝剂也越多。一方面，电流密度越大，产生的絮凝剂越多[20]；另一方面，电流密度越大，阴极还原生成的氢气气泡量越大且气泡尺寸越小[21]，导致气泡密度的增加，更多的小气泡也为油微粒附着于絮凝剂提供了更大的表面积，使得油水分离效率提高。
由图2(b)可见，采用铁阳极对乳化油废水的处理效果要优越于铝阳极。一方面是因为采用铁阳极可以获得较大的电流密度，有利于产生更多的絮凝剂；另一方面，铝阳极氧化过程中易形成致密的表面氧化层，导致电极电阻增大。由于表面氧化层在pH为4~10内的水溶液中非常稳定，氧化层后的铝不易被氧化成铝离子，使得铝离子与氢氧根结合生成的絮凝剂Al(OH)3量减小，絮凝效率变差。
从实验结果可以发现，采用不锈钢-铁电极组合处理含油废水的除油率最高，石墨-铁电极以及钛镀辽铱-铁电极组合处理效果次之，采用铝阳极组合电极处理含油废水的除油率最差。因此，后续均采用不锈钢-铁电极组合进行实验。
2.2 电极间距对极板间电压及除油率的影响
图3给出了不同极板间距下极板间电压及除油率随时间的变化关系。除电极间距外，其他操作参数与电极材料实验时的操作条件相同。由图3(a)可见，随着时间的延长，极板间电压均会降低。其原因在于，电解过程中电极的氧化还原反应均产生阴、阳离子且溶于废水中，会使废水的电导率逐渐增大，废水的电阻减小，极板间电压降低。由图3(a)还可见，随着极板间距的增大，电极间的电压随之增大。这是由于在相同的废水电导率下，极板间距越大，废水的电阻就越大。因此，用来克服溶液间的电阻的电压也就越大。
图 3 不同极板间距下极板间电压及除油率随反应时间的变化Figure 3. Variation of inter-plate voltage and oil removal rate over time at different plate spacing由图3(b)可见，当极板间距由1 cm增大至2.5 cm时，系统的除油率降低。其原因在于，絮凝器电极电阻增大，导致电流密度降低。然而，当极板间距由0.5 cm增大至1 cm时，系统的除油率反而上升。其原因在于，当絮凝器电极间距较小时，适当增大电极间距有利于改善电极间溶液的混合状态，减轻极板附近的浓差极化现象，进而有利于金属离子的溶出，形成絮凝体。
由于需要处理的乳化油废水电导率较低，采用较小的极板间距可以降低用于克服溶液电阻所损失的电压。但极板间距过小时，电极氧化还原反应过程的浓差极化现象较为严重。通过实验发现，对于所研究的RED-EC耦合废水处理系统，采用1 cm的极板间距较为合适。因此，后续实验中极板间距均为1 cm。
2.3 支撑电解质浓度对极板间电压及除油率的影响
支撑电解质浓度变化会影响废水电导率变化，进而会影响电絮凝器电极间废水电阻值，从而影响RED电堆的输出电流和系统的除油率。为了考察支撑电解质浓度变化对除油率的影响，在模拟乳化油废水中添加不同浓度的硫酸钠。图4给出了不同支撑电解质浓度下，极板间电压及除油率随时间的变化关系(除废水中支撑电解质浓度外，其他操作参数与电极材料实验时的操作参数条件相同)。
图 4 不同支撑电解质浓度下，极板间电压及除油率随反应时间的变化Figure 4. Variation of inter-plate voltage and oil removal rate over time at different supporting electrolyte concentrations比较图4(a)和图4(b)可见，当模拟乳化油废水中不添加支撑电解质(硫酸钠浓度为0 mol·L−1)时，极板电压很高，RED电堆的输出电流很小，除油率较低，仅为36.7%。其原因在于，配制的不含支撑电解质的模拟乳化油废水的电导率很低，溶液电阻很大，导致极板间废水所损失的电压很大，RED电堆输出电流减小，除油率降低。当向模拟乳化油废水加入少量支撑电解质(硫酸钠浓度为0.05 mol·L−1)后，废水的电导率会迅速增加，废水的电阻迅速降低，电极电压也随之降低，RED电堆的输出电流随之增加，除油率也随之增大。如果继续增加废水中的支撑电解质浓度，尽管废水电导率会增大，但增大的幅度逐渐变小，对电絮凝器电极电压的影响也会逐渐降低，除油率增速逐渐减小。因此，在采用电絮凝法处理含油废水时，可根据废水的实际电导率来添加支撑电解质量。
2.4 初始pH对极板间电压及除油率的影响
由于含油废水初始pH会影响影响金属氢氧化物(絮凝剂)的形成。因此，该值变化对电絮凝过程会产生较大的影响[22]。为了探索不同初始pH对实验系统除油率的影响，在其它操作参数不变的情况下，通过添加氢氧化钠或硫酸调节废水初始pH(初始pH为3~11)，考察初始pH对RED-EC耦合废水处理系统的除油率的影响关系。
图5给出了在不同初始pH条件下，含油废水pH随处理时间的变化情况。由图5可见，当含油废水初始pH较低时，随着处理时间的增加，废水的pH也会随之增加。其原因是由于在电絮凝过程中阴极还原反应产生了氢氧根(OH−)((5))。但随着含油废水初始pH的增大，随着处理时间而变化的废水pH增速逐渐减小。当初始pH为11时，废水的pH不再随处理时间的变化而变化，几乎保持恒定。
图6给出了不同初始pH条件下，极板间电压及除油率随时间的变化关系。由图6(a)可见，当初始pH偏离7(中性)越多，电极电压相对越低，相应的RED电堆输出电流也就相对越大。其原因在于，添加的酸或碱都属于强电解质，其浓度越高废水的电导率越大，极板间溶液电阻越小，极板间电压越小。当废水初始pH为3时，极板间电压随着处理时间的延长而增大。其原因在于，电絮凝反应产生的部分OH−与酸中的H+中和成水，废水的pH升高(图5)，电导率降低所致。而当废水初始pH为中性或弱碱性时，极板间电压随着处理时间的延长而减小，原因在上述分析中已有阐述。
图 6 不同初始pH条件下，极板间电压及除油率随反应时间的变化Figure 6. Variation of inter-plate voltage and oil removal rate over time at different initial pHs由图6(b)可见，当废水初始pH为中性时，耦合系统的除油率最高。而初始pH太低或太高均对耦合系统的除油率不利。影响耦合系统电絮凝除油效果是多方面的。从预防电极钝化的思路考虑，当pH较低时，电极氧化膜易于溶解，使得电极钝化现象得到延缓。而从絮凝的角度看，中性偏碱性条件更有利于Fe(OH)3絮体形成，以达到较好的絮凝效果[23]。正是由于这两种相互矛盾关系的影响，初始pH在5~9内含油废水经耦合系统处理60 min后的除油率可达到80%以上。
2.5 温度对极板间电压及除油率的影响
电絮凝处理含油废水时，废水温度变化会对除油率产生影响。在电极为不锈钢-铁电极、极板间距1 cm、支撑电解质浓度0.1 mol·L−1、pH为7.8的条件下，不同温度下极板间电压及除油率随时间的变化情况如图7所示。由图7(a)可见，随着电解槽内的含油废水温度升高，电极板间的工作电压降低，RED电堆输出电流增加。其原因在于，随着废水温度的升高，溶解于废水中的金属盐溶质“颗粒”的布朗运动强度增加，溶液电导率增大，电极板间的溶液电阻减小，使得电极电压降低。PAZENKO等[24]研究了废水温度对电絮凝法处理含油废水的影响，得出温度越高，电导率越高，能耗越低的结论。由图7(b)可见，在相同的处理时间内，耦合系统对含油废水的除油率随温度的升高而增加，验证了PAZENKO文献[24]得出的结论。因此，在有条件时，适当提高含油废水温度有利于提高耦合系统处理效率。
图 7 不同温度下极板间电压及除油率随反应时间的变化Figure 7. Variation of inter-plate voltage and oil removal rate over time at different temperatures3. 结论
1)与采用铝阳极材料相比，采用铁阳极材料的耦合废水处理系统具有更高的除油率。
2)极板间距和含油废水参数(电导率、初始pH和温度)变化会对耦合废水处理系统的除油率产生影响。过大或过小的极板间距均对系统的除油率不利，在所研究的系统中，电絮凝器极板间距为1 cm时最佳；当废水的电导率很低时，系统的除油率很小，适当增加废水的电导率可以迅速提高系统的除油率；中性或微碱性条件下系统的除油率较高；温度越高，系统的除油率也越高。
3)采用不锈钢-铁电极，1 cm电极间距，0.1 mol·L−1支撑电解质(Na2SO4)浓度，pH 7.8和40 ℃的实验条件下，经耦合废水处理系统处理60分钟后的含油废水除油率可达到98.39%。
-
图 1 实验装置与场地模型
Figure 1. (a) Electrical resistance heating soil column device and (b) site geometric model
图 2 土柱加入不同体积不同溶液中心点温度实测值与模拟值
Figure 2. Measured and simulated values of the center point temperature of the soil column, added with different volumes of different solutions
图 3 不同电场强度下加热70 d模拟场地横截面温度场
Figure 3. Cross-sectional temperature field of the site heated for 70 days under different electric field intensities
图 4 电场强度对模拟场地中心点温度变化的影响
Figure 4. Effect of electric field intensity on central point temperature of simulated site
图 5 90 V·m−1电场强度下电极间距变化和电极补水对模拟场地中心点温度的影响
Figure 5. Effect of electrode spacing and replenishment of water near the electrode on central point temperature of simulated site under the electric field intensity of 90 V·m−1
图 6 地下水流速对场地横截面温度场的影响
Figure 6. Influence of groundwater velocity on temperature field of site
图 7 地下水上涨速度对场地纵截面温度场的影响
Figure 7. Influence of groundwater rising speed on temperature field of site
表 1 数值模拟参数
Table 1. Numerical simulation parameters
模拟参数 取值 模拟参数 取值 液体密度，ρL 1 000 kg·m−3 温度系数，β 0.02 固体密度，ρS 2 650 kg·m−3 比例常数，α 5×10−6 m2·s−1 气体密度，ρG 1.9 kg·m−3 经验常数，A 8.07131 液体热容，CL 4 200 J·(kg·K)−1 经验常数，B 1 730.63 固体热容，CS 920 J·(kg·K)−1 经验常数，C 233.426 气体热容，CG 1 000 J·(kg·K)−11 胶结系数，m 1.44 湿导热系数，λsat 1.87 W·(m·K)−1 饱和度系数，n 2 干导热系数，λdry 0.23 W·(m·K)−1 水的潜热，ΔHvap 2 257.2 kJ·kg−1 孔隙度，φ 0.5 蒸发速率系数，kvap 1×10−6 s−1 
下载: 导出CSV
表 2 数值模拟工况
Table 2. Numerical simulation conditions
工况 电场强度/ (V·m−1) 初始水饱和度 地下水流速/ (m·s1) 电极间距/m 地下水涨速/ (m·d1) A-1 30 0.6 0 6 0 A-2 60 0.6 0 6 0 A-3 90 0.6 0 6 0 B-1 90/60 0.6 0 3 0 B-2 90/60 0.6 0 6 0 B-3 90/60 0.6 0 9 0 C-1 90 1 0.1 6 0 C-2 90 1 0.2 6 0 C-3 90 1 0.3 6 0 D-1 90 0.6 0 6 0.05 D-2 90 0.6 0 6 0.1 D-3 90 0.6 0 6 0.2
下载: 导出CSV
-
[1] 苗竹, 任贝, 吕正勇, 等. 工业污染场地修复现状[J]. 资源节约与环保, 2020(3): 21-22. doi: 10.3969/j.issn.1673-2251.2020.03.022 [2] BEYKE G, FLEMING D. In situ thermal remediation of DNAPL and LNAPL using electrical resistance heating[J]. Remediation Journal, 2005, 15(3): 5-22. doi: 10.1002/rem.20047 [3] 葛松, 孟宪荣, 许伟, 等. 原位电阻热脱附土壤升温机制及影响因素[J]. 环境科学, 2020, 41(8): 3822-3828. [4] SLEEP B E, MA Y F. Thermal variation of organic fluid properties and impact on thermal remediation feasibility[J]. Journal of Soil Contamination, 2008, 6(3): 281-306. [5] HORST J, MUNHOLLAND J, HEGELE P, et al. In situ thermal remediation for source areas: technology advances and a review of the market from 1988–2020[J]. Ground Water Monitoring & Remediation, 2021, 41(1): 17-31. [6] 田垚, 杨永刚, 韩自玉, 等. 电阻加热条件优化及其对污染土壤中苯并(a)芘的去除[J]. 环境工程学报, 2019, 13(10): 2336-2346. doi: 10.12030/j.cjee.201905176 [7] HIEBERT A D, VERMEULEN F E, CHUTE F S, et al. Numerical simulation results for the electrical heating of athabasca oil-sand formations[J]. Spe Reservoir Engineering, 1986, 1(1): 76-84. doi: 10.2118/13013-PA [8] HIEBERT A D, CAPJACK C E, CHUTE F S, et al. A simulation code for investigating 2D heating of material bodies by low frequency electric fields[J]. Applied Mathematical Modelling, 1983, 7(5): 366-371. doi: 10.1016/0307-904X(83)90136-1 [9] CARRIGAN C R, NITAO J J. Predictive and diagnostic simulation of in situ electrical heating in contaminated, low-permeability soils[J]. Environmental Science & Technology, 2000, 34(22): 4835-4841. [10] MCGEE B C W, VERMEULEN F E. The mechanisms of electrical heating for the recovery of bitumen from oil sands[J]. Journal of Canadian Petroleum Technology, 2007, 46(1): 28-34. [11] KROL M M, SLEEP B E, JOHNSON R L. Impact of low-temperature electrical resistance heating on subsurface flow and transport[J]. Water Resources Research, 2011, 47(5): W05546. [12] 许丹芸, 张亚宁, 朱玲, 等. 基于COMSOL模拟的有机污染土壤ERH修复工艺优化[J]. 环境工程学报, 2021, 15(11): 3642-3650. doi: 10.12030/j.cjee.202101051 [13] TAO G L, LEI D, LIU L S, et al. Prediction of soil water characteristic curve based on soil water evaporation[J]. Advances in Civil Engineering, 2021, 2021: 1-14. [14] YAWS C L, YANG H C. To estimate vapor pressure easily[J]. Hydrocarbon Processing, 1989, 68(10): 65-70. [15] TARNAWSKI V R, LEONG W H, BRISTOW K L. Developing a temperature-dependent Kersten function for soil thermal conductivity[J]. International Journal of Energy Research, 2000, 24(15): 1335-1350. doi: 10.1002/1099-114X(200012)24:15<1335::AID-ER652>3.0.CO;2-X [16] ARCHIE G E. The electrical resistivity log as an aid in determining some reservoir characteristics[J]. Transactions of the AIME, 1942, 146(1): 54-62. doi: 10.2118/942054-G [17] 陈仁朋, 陈伟, 王进学, 等. 饱和砂性土孔隙水电导率特性及测试技术[J]. 岩土工程学报, 2010, 32(5): 780-783. [18] MA R J, MCBRATNEY A, WHELAN B, et al. Comparing temperature correction models for soil electrical conductivity measurement[J]. Precision Agriculture, 2011, 12(1): 55-66. doi: 10.1007/s11119-009-9156-7 [19] HEGELE P R, MCGEE B C W. Managing the negative impacts of groundwater flow on electrothermal remediation[J]. Remediation Journal, 2017, 27(3): 29-38. doi: 10.1002/rem.21516 [20] FU Y W, HORTON R, REN T S, et al. A general form of Archie's model for estimating bulk soil electrical conductivity[J]. Journal of Hydrology, 2021, 59(7): 126160. [21] 唐朝生, 施斌, 顾凯. 土中水分的蒸发过程实验研究[J]. 工程地质学报, 2011, 19(6): 875-881. doi: 10.3969/j.issn.1004-9665.2011.06.012 [22] HAN Z Y, JIAO W T, TIAN Y, et al. Lab-scale removal of PAHs in contaminated soil using electrical resistance heating: Removal efficiency and alteration of soil properties[J]. Chemosphere, 2020, 23(9): 124496. [23] MUNHOLLAND J L, MUMFORD K G, KUEPER B H. Factors affecting gas migration and contaminant redistribution in heterogeneous porous media subject to electrical resistance heating[J]. Journal of Contaminant Hydrology, 2016, 18(4): 14-24. -
点击查看大图
计量
- 文章访问数: 4196
- HTML全文浏览数: 4196
- PDF下载数: 59
- 施引文献: 0
