-
土霉素(oxytetracycline, OTC)是常见的四环素类抗生素,广泛用作抗菌剂。土霉素进入生物体后,约50%~80%无法被吸收,被排出体外。一般而言,抗生素释放到水环境中后,一方面不易被清除,另一方面容易诱变耐药基因,由此造成相关环境风险[1],因此,废水中土霉素的去除研究十分必要。
吸附法广泛用于难降解污染物(如重金属离子、抗生素类、氯代酚类、染料等)的去除。活性炭(AC)具有孔隙多、比表面积大的表面特征,在废水处理领域中主要用于处理重金属、染料、有机物以及净化饮用水等方面[2-3]。但AC价格高,粉末状的AC从溶液中分离回收困难,在吸附过程中常常有质量损失。
磁性材料具有特殊性,可以在外磁场的存在下将固体材料从溶液中分离出来,近10年来受到重视。但直接用磁性材料如Fe3O4作吸附剂,吸附能力差。将活性炭赋予磁性,在保证其基本吸附性能的基础上,能够实现简单分离,解决了AC在使用过程中固液分离困难以及不易回收的问题,在废水处理中的应用范围更加广泛[4-6]。本课题组采用共沉淀法制备了磁性活性炭(MAC),在表征的基础上,研究了其对阳离子染料、氯代酚和硝基酚的吸附性能,发现MAC有较大的吸附量,且可以再生使用,同时具有好的固水分离性能[7-8]。本研究利用盐酸土霉素(OTC-HCl)作为目标物,探讨MAC对OTC-HCl的吸附和解吸特征,并用吸附模型对实验结果进行了拟合,所得结果为其进一步工程化应用提供参考。
全文HTML
-
原料:粉末活性炭(AC,200目)。试剂:FeSO4、FeCl3、NaCl、Na2SO4、CaCl2、盐酸土霉素(OTC-HCl,化学纯)、聚乙二醇,实验所用化学试剂未特殊指明均为分析纯,实验过程中所用水均为蒸馏水。仪器:恒温振荡器(SHZ-82,常州国华电器有限公司)、紫外-可见分光光度计(752,上海舜宇恒平仪器有限公司)、精密酸度计(PHS-3C,上海仪电科学仪器)。
-
采用文献中的方法[8],称取1.6 g AC和0.04 g聚乙二醇,放于水中,搅拌15 min。随后加入2.03 g FeCl3和1.39 g FeSO4,继续搅拌30 min。随后滴加pH=12.5的氨水溶液,直至溶液的pH为11,陈化30 min,恒温水浴50 ℃。反应结束后,用磁铁分离产物,蒸馏水洗涤60 ℃干燥,制得MAC。
表征结果说明,MAC中磁性材料γ-Fe2O3为主要成分,AC约为50%;MAC的饱和磁化强度为5.20 emu·g–1,表面积为1.13 ×103 m2·g−1,MAC的等电点pH为7.09,MAC呈现无规则的颗粒状结构且颗粒尺寸不均匀,大多数微粒尺寸小于1 μm。
采用静态法进行实验,将0.015 g MAC放入50 mL锥形瓶中,加入一定质量浓度的OTC-HCl溶液10 mL,在恒温振荡器进行吸附。一定时间后,采用磁铁分离,取上清液,用分光光度法测定OTC-HCl的浓度,根据吸附前后溶液的浓度差计算。吸附温度分别控制在293、303和313 K。土霉素的测定采用紫外分光光度法,测定波长为269 nm。依据吸收定律,吸光度与OTC的质量浓度在一定范围内呈线性关系。
按固液比为1.5 g·L–1加入MAC和500 mg·L–1 OTC-HCl溶液,于303 K恒温振荡器中吸附600 min,取出锥形瓶,进行磁铁分离,测定上清液中OTC-HCl的浓度,计算方法见式(1)。
式中:qe为单位吸附量,mg·g–1;C0、Ce分别为吸附前后OTC-HCl的浓度,mg·L–1;V为溶液的体积,L;m为吸附剂用量,g。
固液分离后的OTC-HCl-MAC用蒸馏水洗涤数次后干燥,然后用0.01 mol·L–1 NaOH溶液作为解吸液脱附(固液比为1.5 g·L–1),计算解吸率(D,吸附质解吸后进行溶液的量与解吸前吸附剂上的量比值)。将解吸后的MAC用蒸馏水洗涤干燥,进行新一轮的再生实验,计算再生率(再生率为再吸附时单位质量吸附剂的吸附量与第1次吸附时的吸附量比值)。
1.1. 原料、试剂与仪器
1.2. 实验方法
-
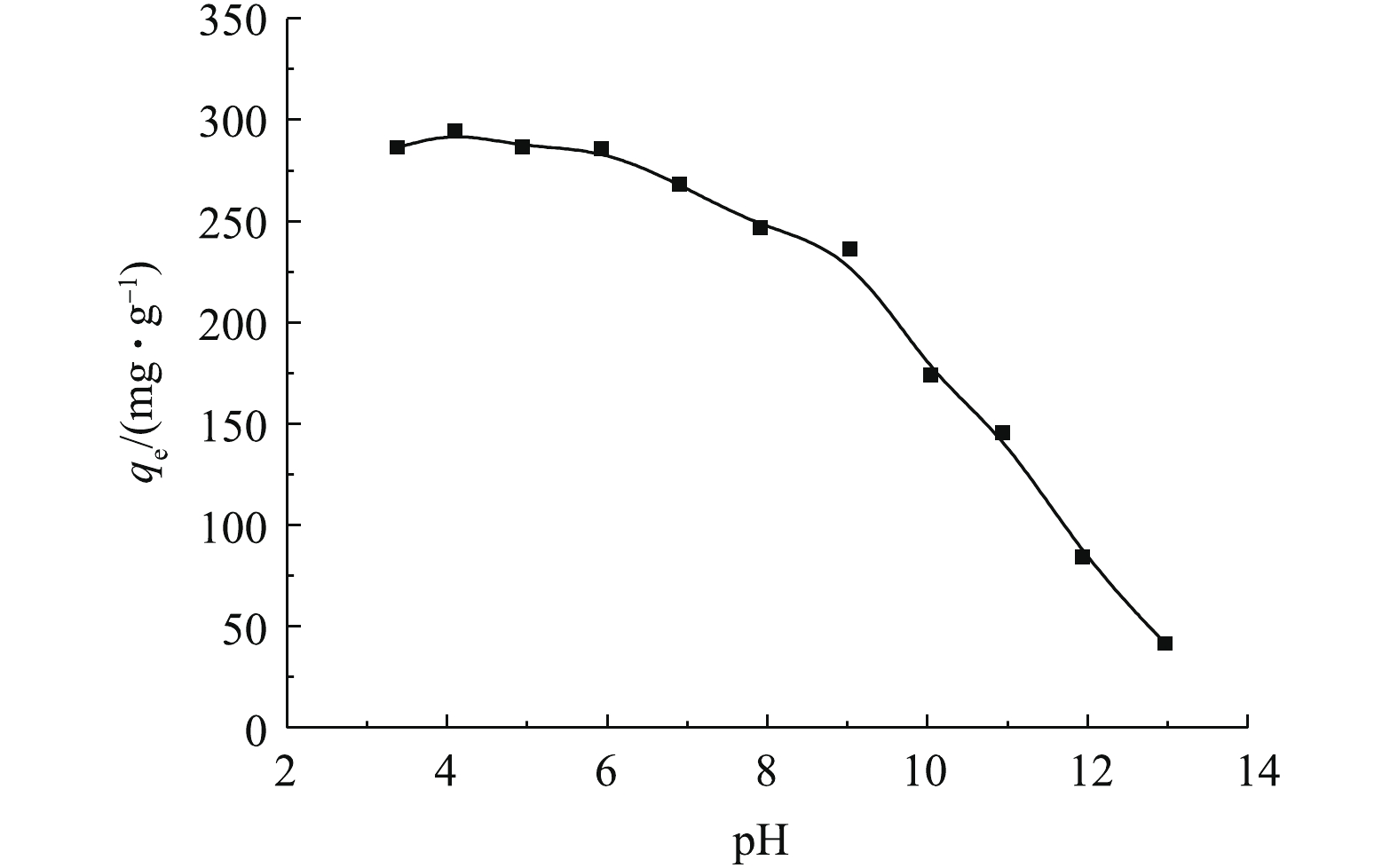
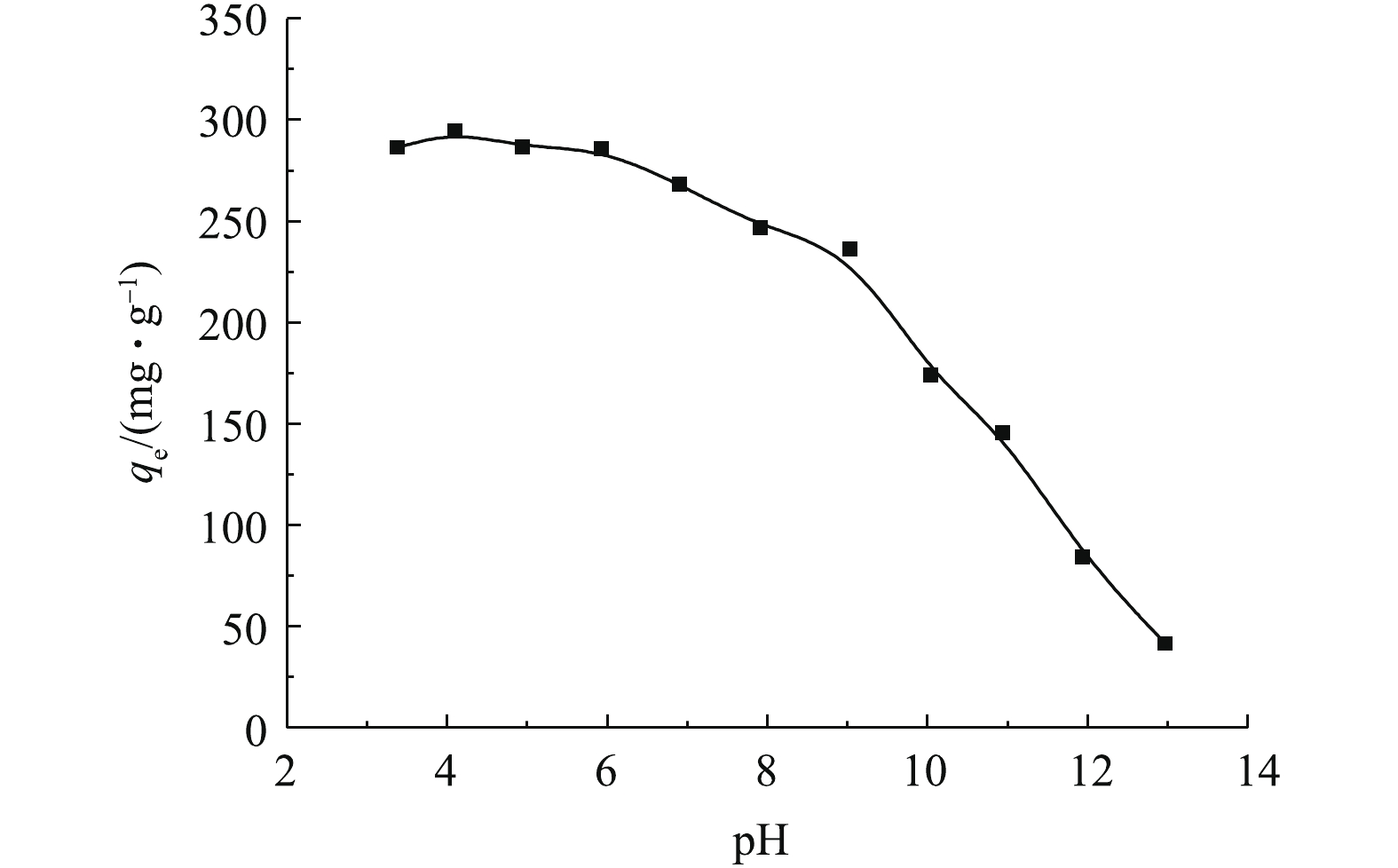
溶液pH不仅影响吸附剂表面的性质,也影响吸附质的存在状态。溶液pH对MAC吸附OTC-HCl的结果如图1所示(C0=500 mg·L−1, t=600 min, T=303 K)。由图1可知,在pH为3~6时,吸附量变化不大,pH超过6时,吸附量逐渐减小。由于OTC-HCl溶液的初始pH为3.40,因此后续实验可以不调pH。
土霉素是一种两性物质,具有多种极性基团,包括氨基和羟基,有两级离解常数(pKa1=3.53,pKa2=9.58)[9]。在pH<3.53时,OTC主要以正离子状态存在;在3.53<pH<9.58时,OTC以两性分子存在;在pH>9.58时,主要以负离子的形式存在。MAC的等电点为7.09,当溶液pH小于7.09时,吸附剂表面带正电,故当溶液pH<3.3时,吸附剂和吸附质之间产生静电排斥,影响吸附作用的进行。当3.53<pH<7.09时,土霉素主要以两性分子状态存在,MAC表面带正电荷,两性的OTC与MAC可能通过静电引力、氢键作用力和范德华力结合,此时OTC-HCl易吸附在MAC表面。当溶液pH>7.09时,OTC与MAC之间形成静电斥力,故MAC对OTC-HCl的吸附能力逐渐降低。
-
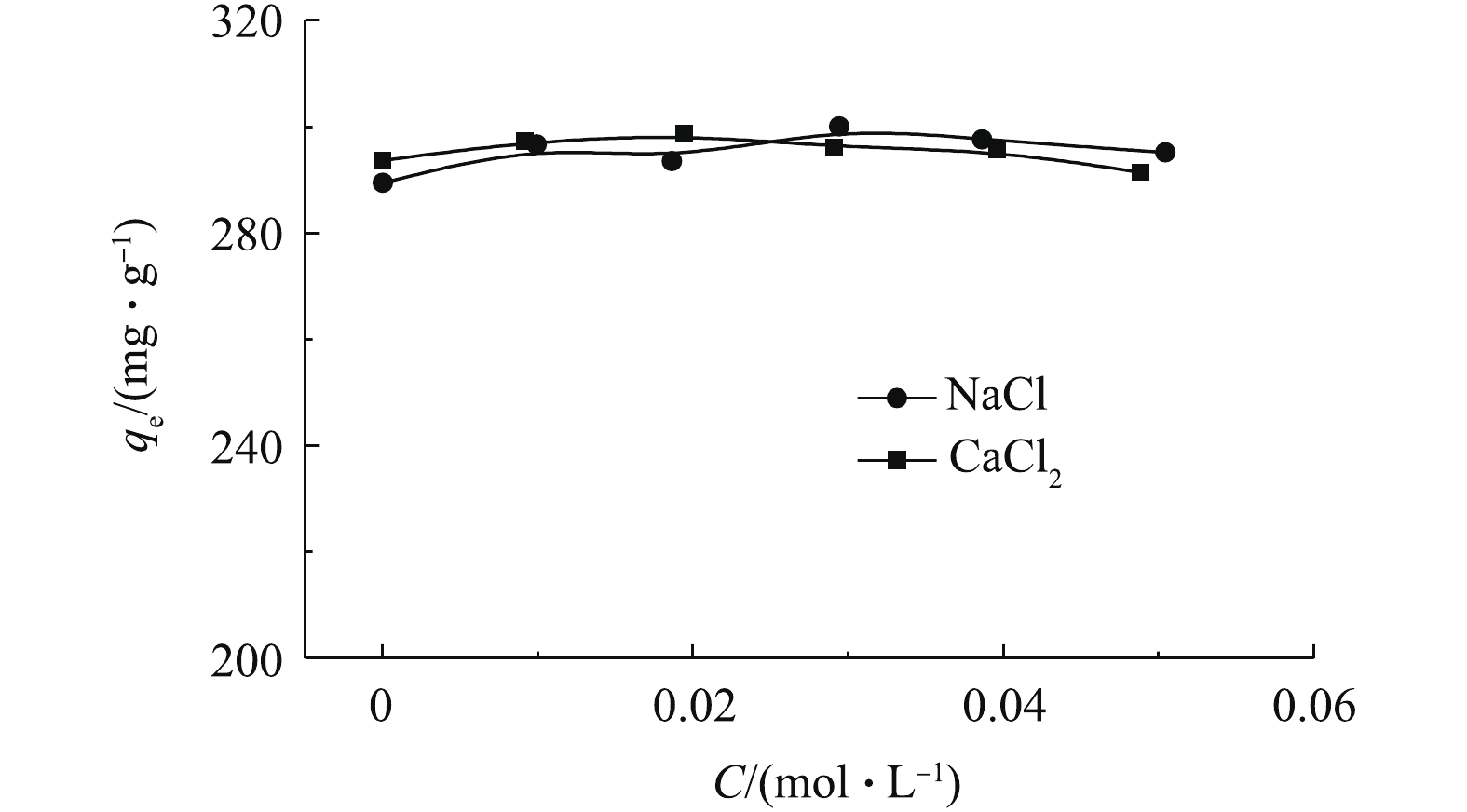
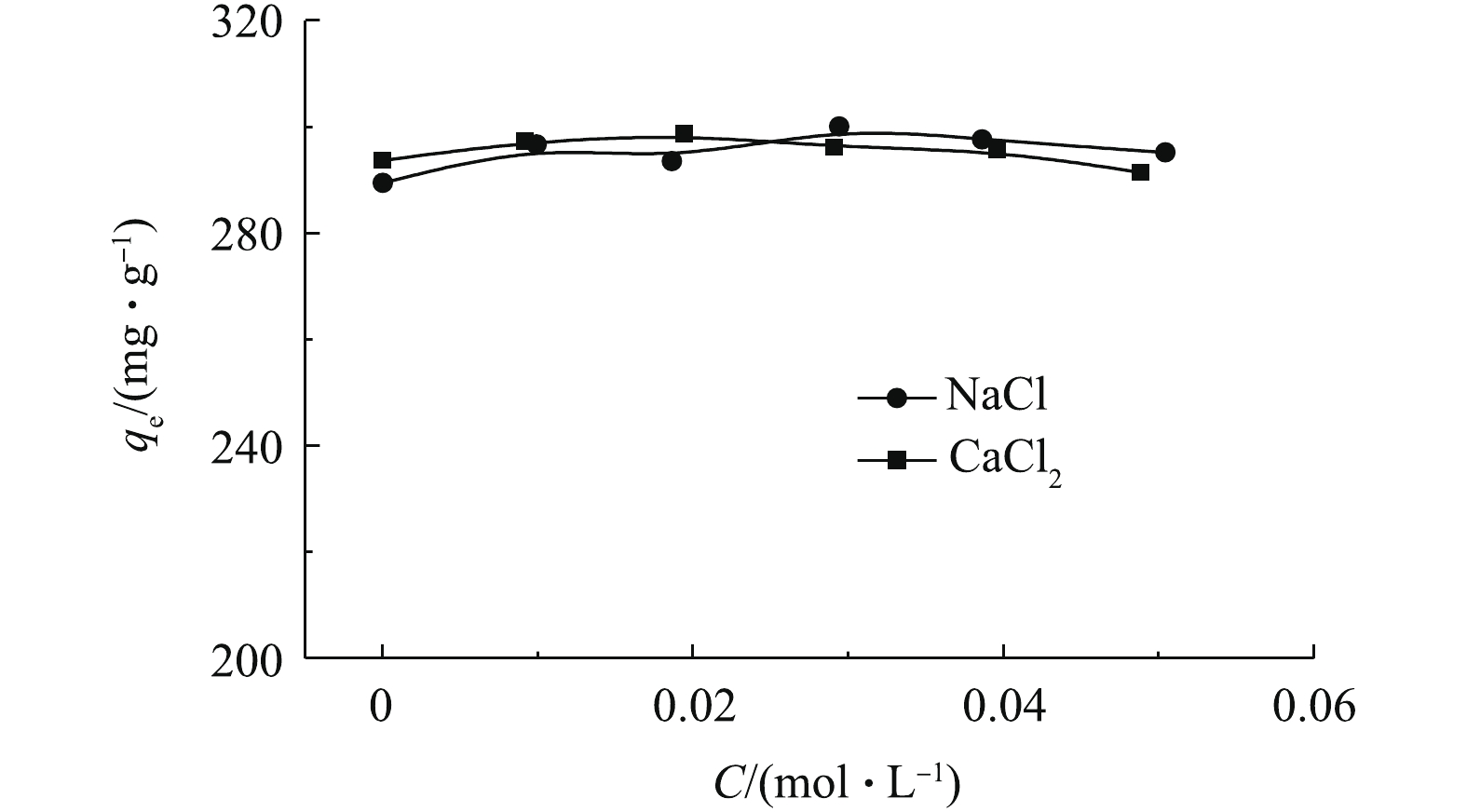
实际废水中常常含有盐类,因此,研究盐浓度对吸附的影响十分必要。不同浓度的NaCl和CaCl2对吸附的影响如图2所示(C0=500 mg·L−1, t=600 min,T=303 K)。可以看出,不同浓度的NaCl和CaCl2对吸附量的影响很小,说明无机盐离子的存在对吸附过程基本无影响,也说明离子交换作用不是主要的吸附机理。采用Mag@ZnO-Co3O4对土霉素进行吸附,得出的结论[10]与本研究一致。
-
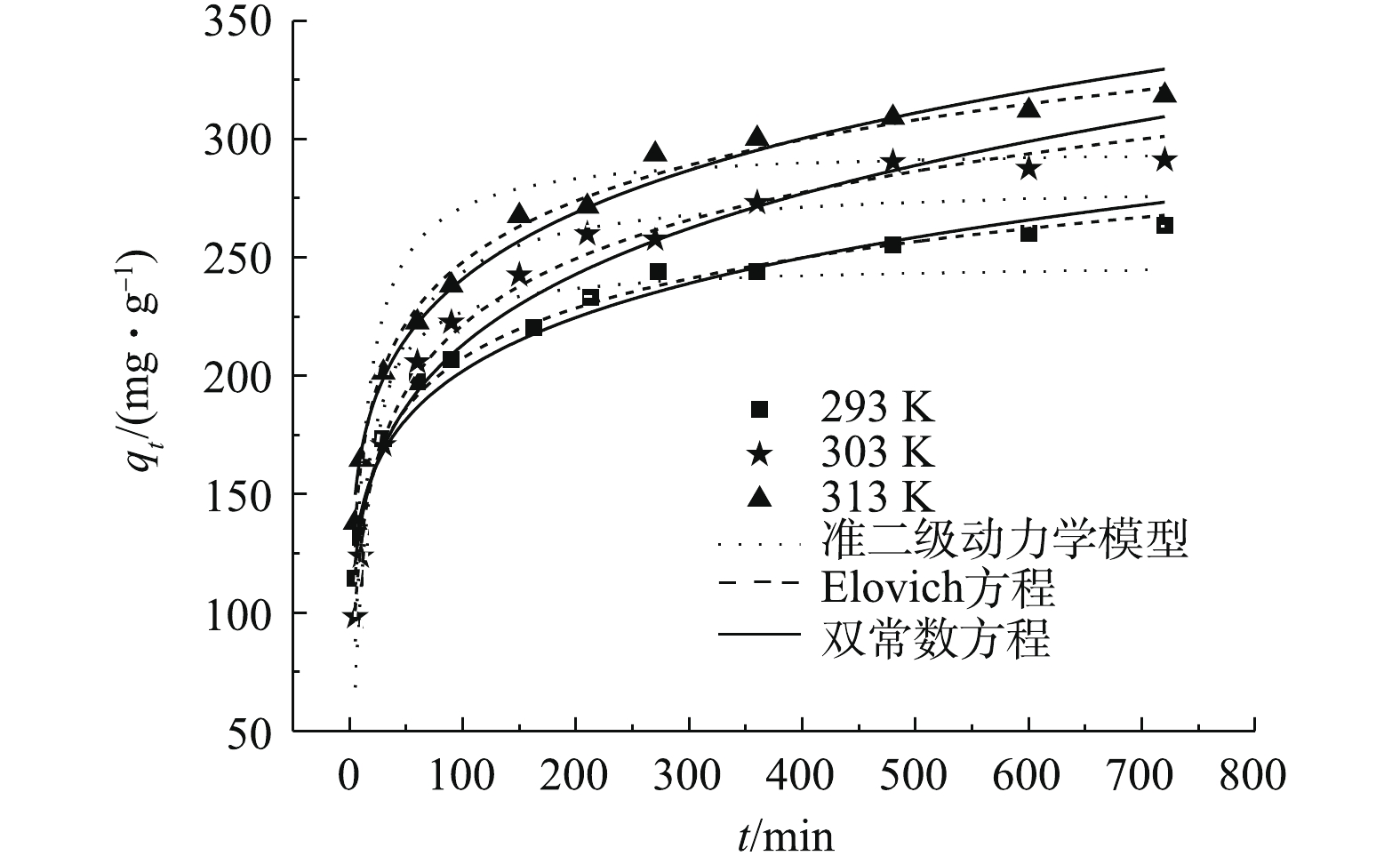
接触时间对吸附的影响如图3所示(C0=500 mg·L−1)。可以看出,随着温度的增加,MAC对OTC-HCl吸附量逐渐变大,说明该吸附过程是一个吸热反应。在同一温度下,随着时间的增加,吸附量迅速变大,然后增加幅度变小,最后趋于平衡。平衡时间超过600 min,说明存在着内扩散的作用。在同样条件下,磁性氧化铁对OTC-HCl几乎没有结合能力。
采用常见的3种动力学模型(见表1)对动力学结果进行非线性拟合分析,结果见表2,拟合曲线见图3。表2中误差按式(2)计算。
式中:E为误差;q为实验结果;qc为理论计算结果。
根据表2的结果,可决系数R2由大到小依次为Elovich方程>双常数方程>准二级动力学模型,误差则依次变大。由图3可看出,Elovich方程的拟合曲线与实验曲线最接近,因此,Elovich方程更好地预测吸附动力学过程。
由t1/2值(吸附量达到平衡吸附量一半时需要的时间)可以计算扩散系数。假定吸附剂为均匀球形颗粒,孔隙扩散系数[7,11-12]可按式(3)计算。
式中:Dp为扩散系数,cm2·s−1;r0为吸附剂直径,cm;t1/2为单位吸附量过半时的吸附时间,s。
由Elovich方程计算出的t1/2,可得温度为293、303、313 K时OTC-HCl在MAC表面的扩散系数,其数值分别为6.00×10−13、3.30×10−13、5.43×10−13 cm2·s−1。所得扩散系数的数量级为10−13,孔隙扩散过程对吸附的影响较大,可以影响吸附速率及平衡时间。
-
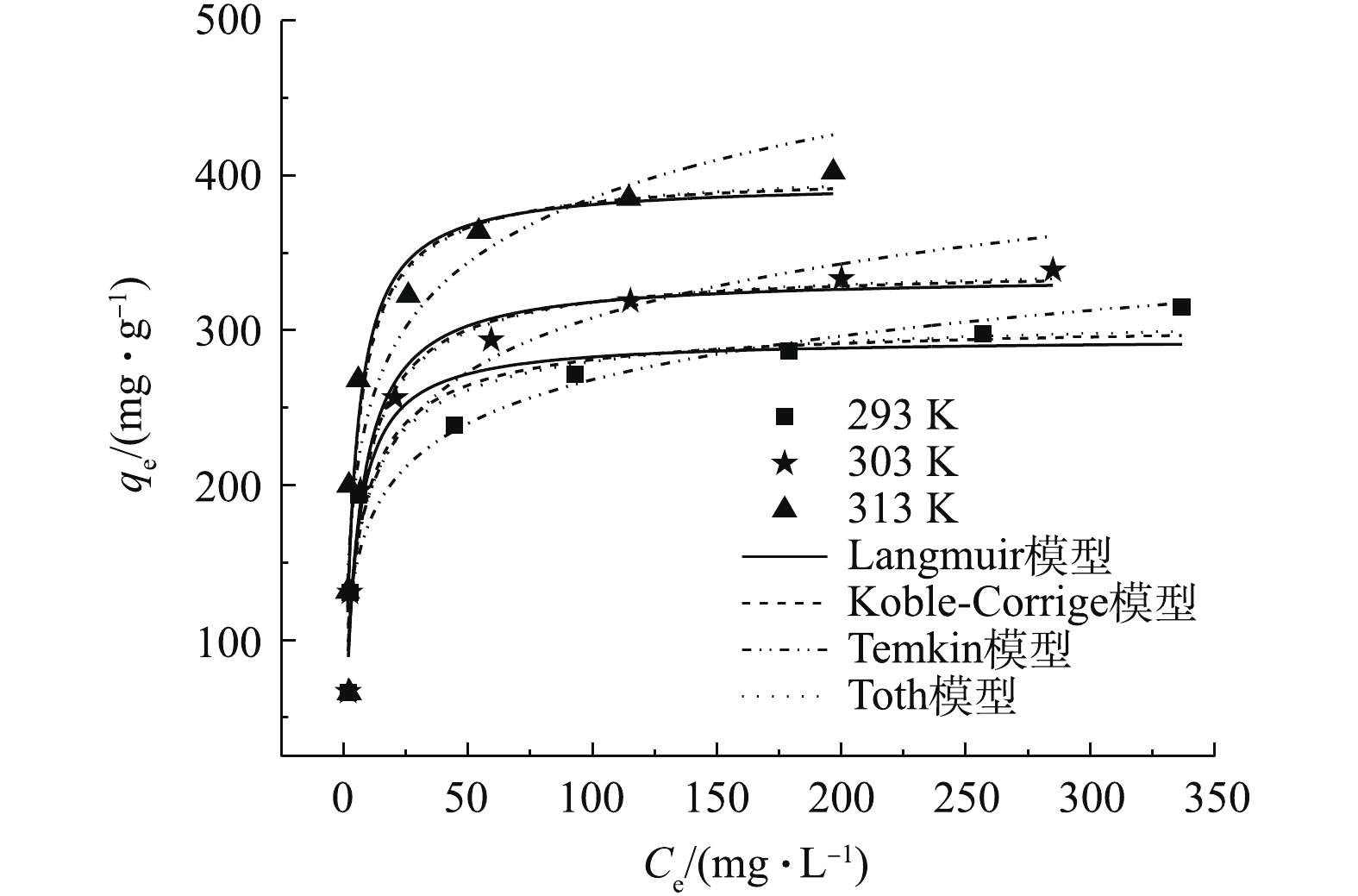
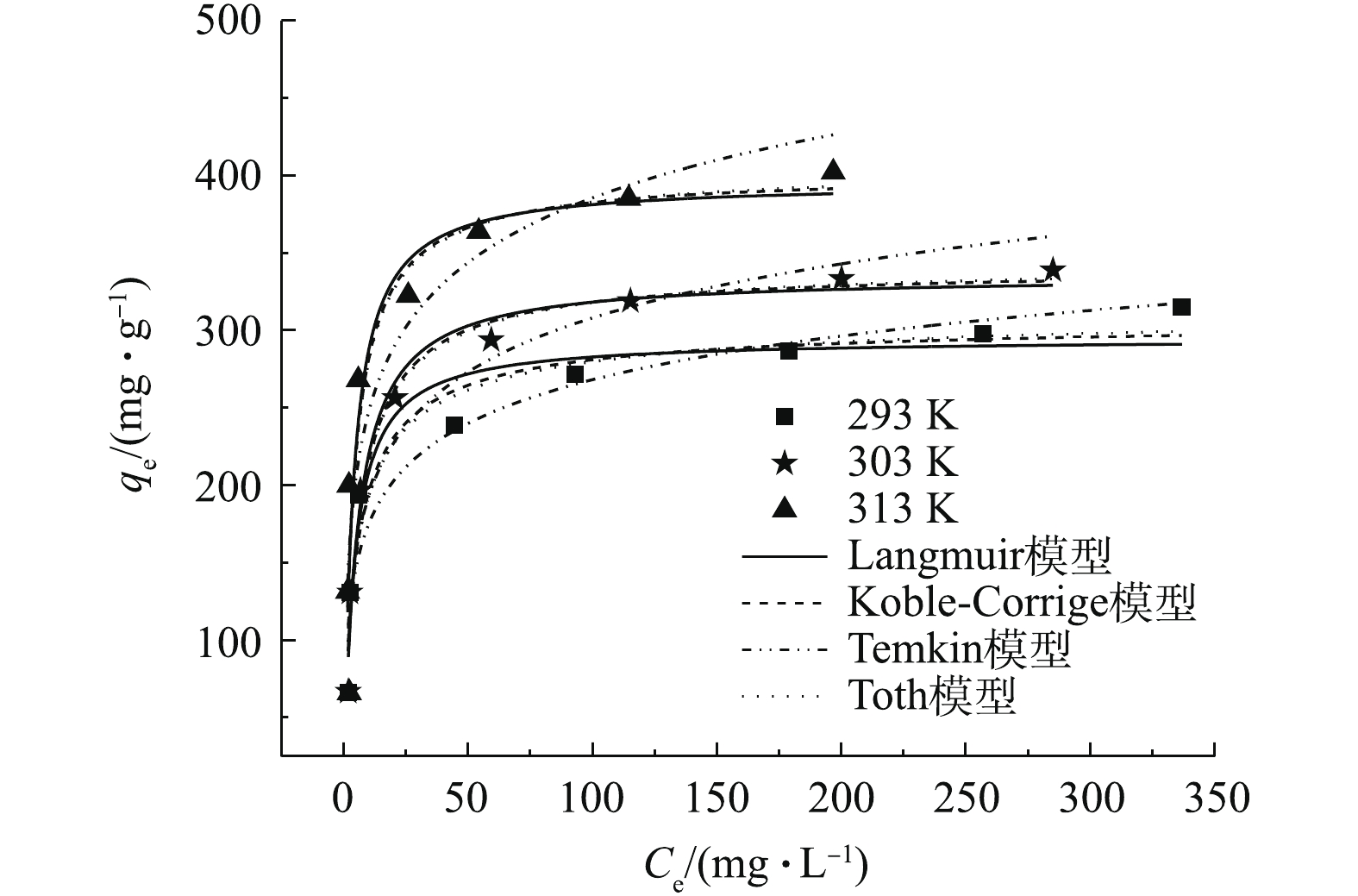
不同OTC-HCl平衡浓度的影响如图4所示。可以看出,在浓度较低时,随着浓度的增加,吸附量迅速变大,随后吸附量增加缓慢,最终趋于平衡。这是因为在浓度低时,MAC具有较多的活性位点,易结合OTC-HCl,随浓度的增加,吸附量增加幅度较大;随着OTC-HCl浓度的增加,单位吸附量缓慢增加,趋势逐渐平缓,是因为MAC的吸附位点被逐渐饱和,吸附逐渐达到饱和状态。由图4还可看出,温度升高有利于吸附。
采用常见的4种吸附等温线模型(方程式见表1)对不同温度下的结果进行拟合,结果见表3,拟合曲线见图4。可以看出,Langmuir模型的R2较大,误差较小,说明该模型可以较好地预测平衡吸附过程。该吸附过程主要是单分子层的吸附过程。另外,qm与实验所得qe接近,且qm和qe均随着温度升高变大,说明该吸附过程是一个吸热反应。Temkin模型适用于多相表面吸附,可以看出,该模型的拟合结果较差,不适合用来描述吸附过程。Koble-Corrigan模型是Langmuir和Freundlich模型的结合形式,拟合所得R2较大,误差较小,可以用于描述其吸附过程。其n值为0.791~0.925,B值为0.204~0.281,MAC吸附OTC-HCl包含单分子和多分子层吸附共存的过程。Toth模型克服Langmuir模型对高浓度和Freundlich模型对低浓度的限制,适应多种类型等温线的拟合。根据表3的拟合结果,发现Toth模型得到的最大吸附量与实验值接近,误差最小,且图4中Toth的拟合曲线与实验曲线最接近,说明Toth模型预测平衡吸附过程最好,也说明该吸附过程含有不均匀表面的吸附。由于在同一条件下,由Toth模型和Koble-Corrigan模型得到的R2值和误差非常接近,因此两者的拟合曲线几乎重叠。
-
吸附剂循环利用可以回收吸附质,也可以提高吸附剂的效率[13-14]。采用0.01 mol·L−1 NaOH溶液作为解吸剂,3次解吸率分别为62.2%、54.2%和47.7%,再生率分别为85.4%、76.0%和75.8%。结果说明MAC有一定的解吸及重复使用性能。
一次解吸时间对解吸率的影响结果如图5所示。可以看出,解吸开始时,解吸速率快,5 min解吸率就达到了26.3%;随后变缓,在480 min时,实现了解吸基本平衡,解吸率达到62.2%。解吸率及再生率下降的原因主要是部分HCl-OTC进入吸附剂孔内部,或与吸附剂结合牢固,不易解吸下来。使用多次后,采用外部磁场仍很容易进行分离,说明磁性稳定。
采用表1的动力学方程对图5的结果进行拟合分析,拟合曲线见图5。拟合结果如下:准二级动力学模型,解吸率=(60.7±1.3)%,k2=(1.88±0.32)×10−3,R2=0.935,误差=88.4;Elovich方程,A=16.1±1.7,B=7.71±0.36,R2=0.978,误差=294;双常数方程,A=12.5±1.1,Ks=0.141±0.020,R2=0.892,误差=16.1。
根据R2、误差和拟合曲线与实验值的比较结果,准二级动力学模型和Elovich方程可以预测解吸动力学,且Elovich方程的R2值最大,误差最小,且该模型主要描述离子交换过程。OTC-HCl-MAC的解吸过程很可能是离子交换的过程。
采用MAC吸附对氯苯酚和对硝基苯酚,也可用NaOH溶液进行再生,解吸过程可用准二级动力学模型和Elovich方程预测,但准二级动力学模型更准确[7],这与本研究的结果有区别。阳离子表面活性剂改性树叶对2,4-二氯苯酚有较好的吸附能力,用75%乙醇溶液解吸,准二级动力学模型可拟合解吸结果[15],这也与本研究的结果有差别。
2.1. 溶液pH对吸附效果的影响
2.2. 溶液盐度对吸附效果的影响
2.3. 吸附时间的影响
2.4. OTC-HCl浓度的影响
2.5. 吸附剂的解吸及再吸附性能
-
1)溶液pH影响MAC对OTC-HCl的吸附量,共存盐的影响小,升温有利于吸附。
2) MAC对OTC-HCl的吸附过程符合Langmuir模型和Elovich动力学模型,推测该过程是单分子层的非均相扩散过程。
3)吸附OTC-HCl后的MAC有一定的解吸再生性能,MAC可用于水体中此类污染物的去除。



 下载:
下载: