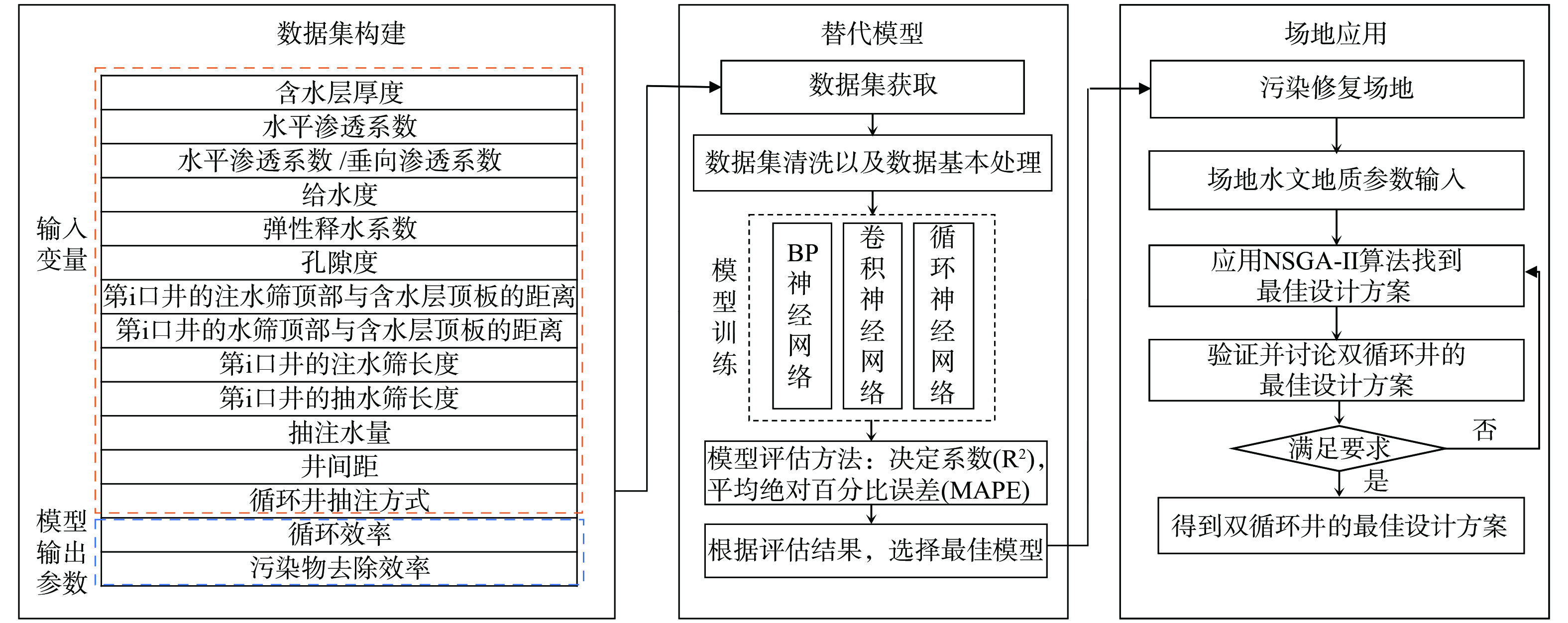
本研究的研究思路主要分为3个基本步骤，具体流程如图1所示。

1) 双循环井简介。双循环井具有多种结构形式，本研究以2个典型循环井组成的循环井对为研究单元。循环井包含2个由阻隔器分隔开的筛管 (抽水筛和注水筛) ，受污染的地下水通过抽水筛抽出，经处理后再通过注水筛以相同流量注入含水层。地下水在循环井周围形成环流场，而相邻两井的循环模式不同，引起的水流流向不同，且相邻井之间产生互相扰动。主要有两种不同的情况，即循环方式相同 (如图2(a)) 和循环方式相反 (如图2(b)) 。

2) 数据集构成。利用FloPy软件包和Python开发双循环井数值模型，利用该数值模型建立包含输入变量和模型输出参数的数据集。如图1所示，输入变量主要包括双循环井运行效果的影响因素 (水文地质参数、循环井结构参数以及运行参数^[19-20]) ，输出变量为模型输出双循环井运行180 d后^[10,21]的运行效果表征参数 (循环井群循环效率、污染物去除效率^{[10,19,21-22]}) 。其中循环井抽注方式 (相邻井抽注模式相同或相反) 的确定在本次研究中由循环井结构参数中抽注水筛的位置关系决定。循环井分为上抽下注和上注下抽2种抽注模式，即循环井抽水筛顶部与含水层顶部的距离小于注水筛顶部与含水层顶部的距离，则该循环井抽注模式为上抽下注模式，反之则称为上注下抽模式。

3) 数值模型求解。将输入变量输入到数值模型中，利用地下水流模拟程序 (MODFLOW) 、粒子追踪模拟程序 (MODPATH) 和溶质运移模拟程序 (MT3DMS) 分别进行双循环井地下水流、运动轨迹及污染物运移的数值模拟计算，根据MODPATH建立粒子追踪模型，以所有循环井的循环粒子数与投放总粒子数的比作为循环井群循环效率；此外根据MT3DMS模拟污染物在地下水中的运行过程，以运行时段末与运行前场地污染物的变化总量与初始污染物总量的比作为污染物去除效率^[23-25]。最终形成输入变量和模型输出参数共同组成的数据集。

卷积神经网络 (convolutional neural networks，CNN) 是一种具有多个处理层的神经网络模型，主要由卷积层、池化层和全连接层这3类层组成，通过将这3类层按照不同数量及顺序叠加起来，即可构建出一个完整的卷积神经网络^[26]。本研究根据已获得的双循环井数据集，利用卷积神经网络模型学习双循环井影响因素与运行效果响应之间的映射关系。卷积神经网络模型的训练基于损失函数的计算结果，将误差进行反向传播到卷积神经网络的各个层，各层根据误差的反馈进行参数权值的更新。之后随着模型的训练、验证过程的进行，将卷积神经网络的结构及其他参数进行不断优化，从而使基于深度学习方法的替代模型与数值模拟模型达到最佳拟合。

根据前述样本空间的参数选取以及模型求解得到的双循环井性能指标，本研究共利用已有的800个数据集样本，随机抽取600组为训练集、100组为验证集和100组为测试集。其中训练集在卷积神经网络的训练过程中，通过梯度下降的方式减小训练误差，并得到模型内置参数，使模型获得预测双循环井运行效果表征参数响应的能力；验证集用于调整模型的网络结构和超参数，并对模型的能力进行初步评估；测试集用于最后模型精确度的评估。

在模型的构建上，本研究采用自适应动量优化 (adaptive moment，Adam) 算法优化卷积神经网络建立的替代模型，使用均方误差 (mean squared error，MSE) 作为损失函数，为了确定卷积神经网络模型中的网络结构和超参数，尝试了多种组合，并最终确定了误差最小的卷积神经网络模型结构，实验结果为建立的模型结构包括交替连接的3个卷积层和3个最大池化层、1个展平层和3个全连接层。另外该模型的核心参数配置：每批样本为50，迭代次数为3 000，激活函数均为线性整流函数 (rectified linear unit，ReLu) ，卷积神经网络内部参数如图3所示。

1) 目标函数。在本研究中，通过循环效率和污染物去除效率来衡量双循环井的运行效果，循环效率 (Pr) 是衡量双循环井抽水筛对地下水捕获能力的指标，可以体现水力环流的闭合性。较高的循环效率不仅可以保证修复试剂的充分利用，也可以保证污染组分再双循环井系统中得到降解，从而避免污染物从双循环井的环流场逃逸，造成二次污染。可以利用MODPATH计算，从而通过数值模型量化该指标。另外双循环群修复的最终目的是高效捕获和去除地下水中的污染物，所以将污染物去除效率 (η) 也作为指标。因此目标函数的数学表达式可以表示为式(1)和式(2)。

式中：${N}_{inj}$为注入的粒子数；${N}_{rec}$为随时间t变化的粒子回收数；$Conc$表示场地初始污染物浓度；$Conc'$表示双循环井运行180 d后污染物浓度。

2) 约束条件。循环井群主要受到以下3种类型的约束条件的影响，即循环井所在位置的约束条件，循环井筛管的约束条件和流量的约束条件。

①循环井位置的约束条件，本研究主要考虑双循环井的设计方案，假定以第一个井的位置为原点 (0，0) ，第二个井的位置则为 (0，d) ，则井间距的约束条件见式(3)。

式中：${d}_{{\mathrm{max}}}$根据待修复场地的具体大小得到的可布置的两个循环井之间的最大井间距，m，该参数由场地大小决定。

②筛管位置的约束条件，保证每个循环井的上下筛管位置均位于含水层中，是使用循环井技术的必要条件^[4]，则筛管位置的约束条件见式(4)。

式中：${d}_{{\mathrm{in}}}^{i}$表示第i口井注水筛顶部与含水层顶板的距离，m；${d}_{{\mathrm{out}}}^{i}$表示第i口井抽水筛顶部与含水层顶板的距离，m；${L}_{{\mathrm{max}}}$为筛管的最大长度，m；M表示含水层的厚度，m。

③循环井流量的约束条件，假设循环井每个井的抽注流量大小相等，则循环井流量的约束条件见式(5)。

式中：${Q}^{i}$表示为第i口循环井抽注流量，m³∙d⁻¹；${Q}_{{\mathrm{in}}}^{i}$表示第i口井的注水筛流量，m³∙d⁻¹；${Q}_{{\mathrm{out}}}^{i}$表示第i口井的抽水筛流量，m³∙d⁻¹；${Q}_{{\mathrm{max}}}$表示为抽注流量的最大值，该参数由水文地质参数决定^[27]，各参数的含义详见图2。

3) 基于NSGA-Ⅱ算法的双循环井参数多目标优化。双循环井优化问题实际上是一个具有多个变量以及多目标函数的复杂优化问题。目前用于解决多目标优化问题的方法很多，比如遗传算法，NSGA算法，粒子群算法等。NSGA-Ⅱ算法比其他优化算法适用性更加广泛，在复杂应用场合上效果更好^[28]。NSGA-Ⅱ算法的基本流程如下。

①首先随机初始化父代种群P₀，种群规模为P，对父代种群进行非支配排序后，经过选择、交叉和变异遗传算子生成第一个子代种群N₀。

②从第二个子代种群开始，将初始化父代种群P₀和第一个子代种群N₀合并为新种群K₀，对K₀种群进行非支配排序后，对每个非支配层的个体计算拥挤度，并根据非支配关系和拥挤度选取N个个体组成父代种群P₁，再采用遗传算子产生新一代种群N₁。

③以此类推，直到进化代数gen达到设定的最大遗传代数gen_max时停止计算，得到Pareto最优解集。

为了保证NSGA-Ⅱ算法的全局寻优能力，准确且快速的找到最优解集，模型参数设置如下：初始化种群个数100；迭代次数300；选择模拟二进制交叉算子 (SBX) ；交叉概率0.8；使用多项式变异 (PM) ；变异概率0.2。通过求解优化模型，即可获得约束条件下的双循环井污染物去除效率和循环效率。

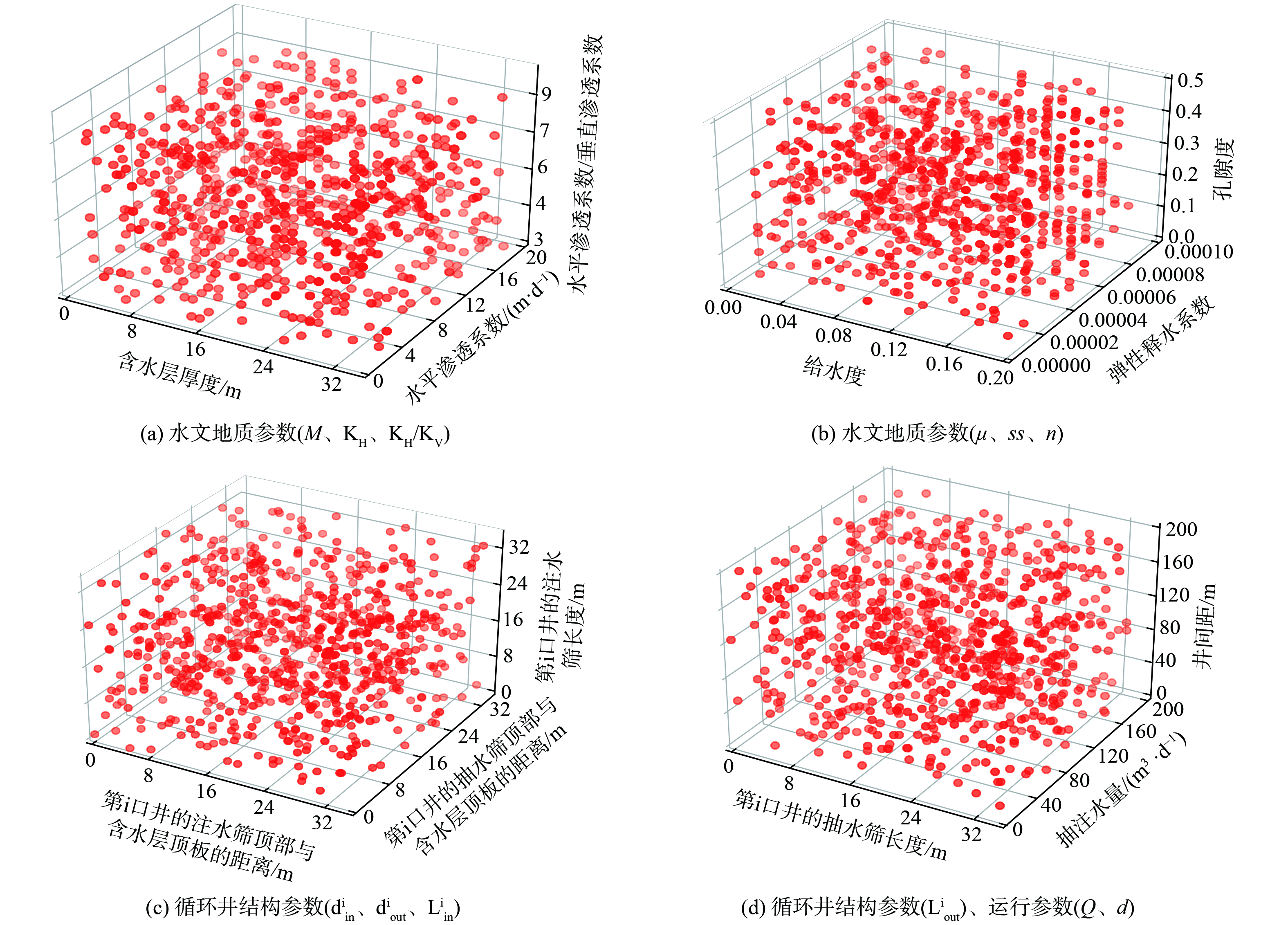
本研究中通过数值模型建立了包含输入变量和模型输出参数共同组成的有效数据样本800个，数据集的主要指标见表1。该数据集是用于训练替代模型的训练样本，训练样本覆盖越广泛，样本数越多，越能保证训练效果，使替代模型能够更好的拟合数值模型中输入输出的响应关系。由图4可知，该数据集中各输入变量的分布基本覆盖了循环井适用的全部范围，表明通过数值模型获取的数据集具有代表性。

评估训练后替代模型的精确度，选取100组数据作为测试集，对训练后的替代模型进行测试，以评估模型泛化能力。此外，为证明本研究中卷积神经网络替代模型的性能，选取深度学习模型中的反向传播 (back propagation，BP) 神经网络模型和循环神经网络模型 (recurrent neural networks，RNN) 进行对比。

利用Tensorflow平台建立卷积神经网络、BP神经网络和循环神经网络3种深度学习模型，以决定系数 (r-square，R²) 、平均绝对百分比误差 (mean absolute percentage error，MAPE) 作为评价替代模型的精确度的指标，R²越接近于1，表示替代模型的精确度越高；MAPE越接近于0，表示替代模型的精确度越高。其计算式如式(6)~式(7)所示。

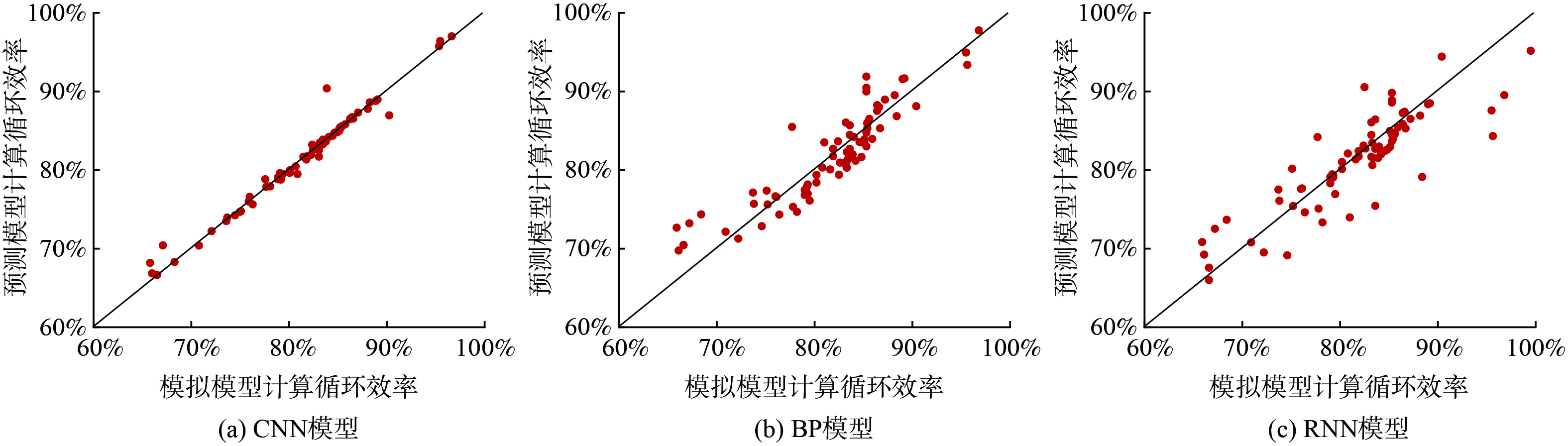
式中：n表示样本个数，i表示样本编号，${\hat{y}}_{i}$表示替代模型输出值，${y}_{i}$表示模拟模型输出值，${\stackrel{-}{y}}_{i}$表示模拟模型输出值的平均值。各模型的预测结果具体如图5、6所示，结果表明CNN模型效果预测效果越好。

几种预测模型对双循环井运行效果表征参数的精确度R²和MAPE如表2所示，可知3种预测模型对循环效率的预测效果均比污染物去除效率要好；另外，无论是预测循环效率还是污染物去除效率， CNN模型的精确度都要优于另外两种深度学习模型。CNN模型对于循环效率的精确度R²达到0.972，MAPE达到0.008；而对于污染物去除效率的精确度R²达到0.946，MAPE达到0.009。

综上所述，基于卷积神经网络的替代模型和数值模型具有较高的拟合精度并且具有强大的泛化能力，可以更好地反映数值模拟模型的输入输出变量响应关系，并且可以嵌入优化模型中，保证了双循环井优化方案的可靠性。

本研究选取陕西省西安市某示范场地为研究区，针对场地实际水文地质条件开展双循环井优化设计。该场地位于关中盆地渭河河谷阶地中部，场地东西长180 m，南北宽60~70 m。试验目标含水层为第四系全新统、上更新统冲积孔隙潜水含水层。含水层以中砂为主，赋水性良好，含水层厚度 (M) 为13.5 m、水平渗透系数 (K_H) 为20 m∙d⁻¹、水平渗透系数/垂向渗透系数 (K_H/K_V) 为3、给水度 (μ) 为0.2、弹性释水系数 (ss) 为0.0001、孔隙度 (n) 为0.39。将该试验场地的水文地质参数输入到测试后的双循环井多目标优化设计模型中，以获取适合该场地的优化设计方案。

将试验场地的水文地质参数输入双循环井运行效果预测模型中，并利用NSGA-Ⅱ算法求解适合该试验场地的双循环井结构及运行参数的最优组合，从而实现双循环井的优化设计。NSGA-Ⅱ优化算法求解结果可采用超体积指数指标 (Hypervolume) 指标来评价。如图7所示，在迭代70次后，优化算法收敛至较优水平，并逐渐寻找最优解，证明该算法可行。

在获得的Pareto最优解集中选择4个典型方案进行对比，优化方案如表3~表4所示。其中方案1和方案2的2个循环井抽注模式相同 (均为上抽下注模式) 。方案1循环井的循环效率低于方案2，而污染物去除效率高于方案2；2种方案的抽注水量相同，但方案2的井间距小于方案1。井间距越小，循环井间互相扰动越强，而多个循环井间的相互扰动对单井的循环效率起着促进作用，因而整体的循环效率变高。

方案3和方案4的两个循环井抽注模式不同。方案3循环井循环效率低于方案4，而污染物去除效率高于方案4；2种方案的抽注水量相同，但方案4的井间距小于方案3。井间距越小，循环井间互相扰动越强，因此抽注模式相反方案中循环井间相互扰动同样对单井的循环效率有积极的影响。

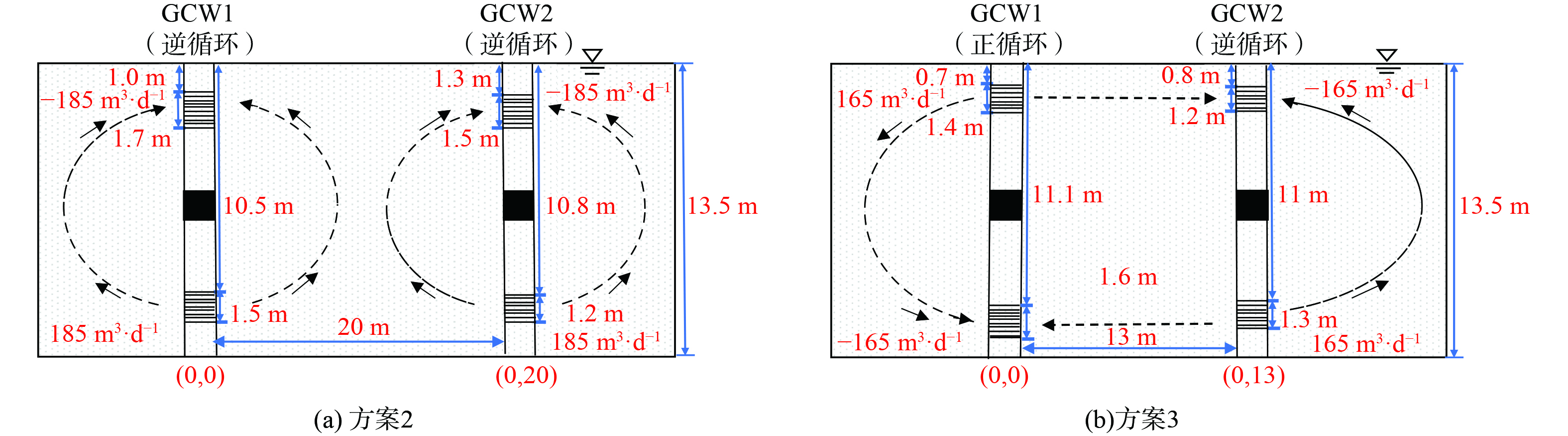
多目标优化设计模型得到的优化设计方案均可以得到较高的循环效率和污染物去除效率，因此在双循环井的实际应用中，可进一步根据优化时的侧重点选择其中更符合实际需求的设计方案。例如当污染场地修复工期较长时，可侧重于保证修复试剂的充分利用，同时为防止污染物从双循环井的环流场逃逸而污染下游地下水，可选择循环效率最优的方案2作为最终优化设计方案；而当修复工期较短时，可侧重于保证场地污染物去除效率更高，则可选择污染物去除效率最高的方案3作为最终的优化设计方案。方案2和方案3的设计参数如图8所示。

将表3列出的优化设计参数代入到前述双循环井模拟模型中求解，将优化模型与模拟模型得到的结果进行相对误差计算，其计算式如式(8)所示。

式中：$\sigma$表示相对误差，${x}'$表示优化模型求解结果，x表示模拟模型求解结果。

计算对比结果如表4所示，循环效率的最大相对误差为3.4%，污染物去除效率的最大相对误差为3.8%，相对误差均低于±5%，证明该NSGA-Ⅱ优化模型的计算结果可靠。

1) 考虑到水文地质参数的不确定性，深度学习方法中基于卷积神经网络的替代模型与地下水数值模型有很大的适应性，可以稳健地反映地下水数值模型的输入输出关系。本研究选取确定性系数 (R²) 、平均绝对百分比误差 (MAPE) 2个指标去评价替代模型的精确度。结果表明替代模型一方面减少了计算负荷，同时在预测双循环井循环效率时的R²达到0.972，MAPE达到0.008；污染物去除效率的R²达到0.986，MAPE达到0.009，计算精度高。说明构建基于卷积神经网络的替代模型在双循环井的优化设计中是可行的。

2) 通过对双循环井优化设计方案的验证，发现得到的双循环井运行效果较好，验证了优化设计方案的可靠性，也表明了优化设计在双循环井实际使用工作中的必要性。本研究在获得的Pareto最优解集中选取4个典型方案进行对比分析，并最终确定了两个不同优化目标下的最优方案。本研究中的双循环井优化设计方法可以获取不同水文地质条件下双循环井结构及运行参数、井间距等指标，从而保证循环井的运行效果，达到该技术在地下水污染治理中的合理应用。