-
静电除尘器具有处理风量大、阻力能耗低、耐高温、除尘效率高等诸多优点，被广泛应用于工业尾气颗粒物净化领域[1-2]。电除尘设备除尘性能受到电场结构、电场电压、气流速度等众多因素的影响[3-5]。其中，电场结构直接影响电场分布和流场分布，进而影响除尘效率[6-7]，故电场内部电极排列布置对设备除尘性能影响较大。
国内外学者做了大量关于电场结构优化相关的研究工作。依成武等[8]设计了单区双涡旋型极板电除尘器，通过实验证实了电压、收尘面积、流速以及粉尘粒径等对除尘效率的影响，并发现当电极电压约为18 kV、有效收尘面积为2.7 m2时，除尘效率最大。胡建华等[9]发现，改变极板间距会影响荷电颗粒的沉降速度与运动轨迹，电极线间距存在一个最佳值。张立莹等[10]研究得出，增大极板间距会降低电场强度和颗粒的荷电量，最终致使颗粒捕集效率下降。崔晓慧等[11]对新型阳极板进行排布优化研究，证明错位板排布有利于提高对微细粉尘的收集效率。AHMED等[12]研究了线板式电除尘的电场特性，得出减小线间距会增大放电电流值的结论。DONG等[13]研究表明，放电极间距在大于150 mm时，颗粒捕集效率没有明显提升，设定合适的放电极间距对电除尘器的设计至关重要。又有研究人员[14-16]提出，极板极线间距在符合一定比例时具有较好捕集效率，优化极-板间距对提高电除尘效率有重要作用。
本研究拟利用电晕电场模型、k-ε湍流模型、Lawless电荷累积模型来建立新的静电除尘多场模拟模型，并通过改变极板间距和极线间距，分析电场电势、风速、颗粒运动轨迹、除尘效率的变化特征，以揭示极线间距和极板间距对线板式除尘器效率的影响，从而为线板式电除尘内部结构和电极排布的优化和设计提供参考。
-
线板式静电除尘器电场内部由收尘极板和电极线组成，如图1所示。其工作原理是：电极线与收尘极板之间形成高压电场，电极附近产生电晕放电，致使空气发生电离；当含尘气流穿过电晕区时，粉尘颗粒物在库仑力的作用下向收尘极板运动，被收尘极板捕集，实现气固分离、净化空气的目的。
本实验通过调节两收尘极板和电极线的间距监测电场内电势和风速，在收尘极板至第2根与第3根放电极中间 (即ab线) ，和第1根电极至收尘极板 (即cd线) 设置监测位，监测并收集数据。
-
本研究依据带电粒子传输电流的守恒性建立电晕模型，故使用电流连续性方程和Poisson方程来求解带电粒子输运问题[17]。电晕模型的控制方程见式 (1)~(4) 。
式中：J为电流密度，A·m−2；kion为离子迁移率，(m2·V−1·s−1)；ρion为离子电荷密度，C·m−3；E为电场强度，V·m−1；Dion是离子扩散系数，m2·s−1；ɛ0为真空介电常数；V为电势，V。
-
湍流模型使用动量守恒的Navier-Stokes方程和质量守恒的连续性方程进行求解，见式 (5)~(7)。
式中：μc为层流黏度系数，kg·m−1·s−1；μT为湍流黏度系数，kg·m−1·s−1；ρ为流体密度，kg·m−3；I为单位矩阵；p为气体静压力，Pa；FEHD为电流体力，N·m−3。
标准k-ε湍流模型由湍动能方程和耗散率方程组成，控制方程见式 (8)~(10) 。
式中：k为湍流动能；ɛ为湍流耗散率；Pk为湍动能每单位耗散净产出；湍流场参数：σk为1；σε为1.3；Cε1为1.44；Cε2为1.92；Cε3为0.09。
-
根据牛顿第二运动定律，对颗粒位置矢量分量的二阶运动方程进行求解，以求得运动颗粒的位置，控制方程见式 (11)~(12) 。
式中：q为颗粒的位置，m；v为颗粒运动的速度，m·s−1；mp为颗粒的质量，kg；Ft为施加在粒子上的合力，N。
使用LAWLESS模型[18]计算颗粒上累积的电荷，计算方程见式 (13)~(14) 。
式中：v=(qpe/2πε0dpkBT)，其含义为无量纲的粒子荷电；w=(εp/(εp+2))(Edpe/2kBT)，其含义为无量纲的电场强度；qp为颗粒荷电量，C；e为电子的电荷，1.6×10−19C；dp为颗粒直径，m；kB为玻尔兹曼常数，1.3806×10−23 J·K−1；T为热力学温度，K；εp为颗粒介电常数；τ=(ρionkiont/ε0)，其含义为无量纲的充电时间；ρion为离子电荷密度，C·m−3；kion为离子迁移率，m2·V−1·s−1；t为实际荷电时间，s。
模型求解共分为两步。第一步是稳态计算，计算电场、电荷传输、湍流场和多物理场耦合。基于稳态计算的结果再进行第二步瞬态计算，计算流体流动颗粒追踪。最终得出颗粒在电场、流场的运动轨迹和除尘效率。
-
为验证数值模拟模型的可靠性和准确性，选取前人的实验数据作为基准，采用COMSOL软件建立模型对静电除尘器性能进行数值模拟，将模拟结果与实验数据进行验证。
-
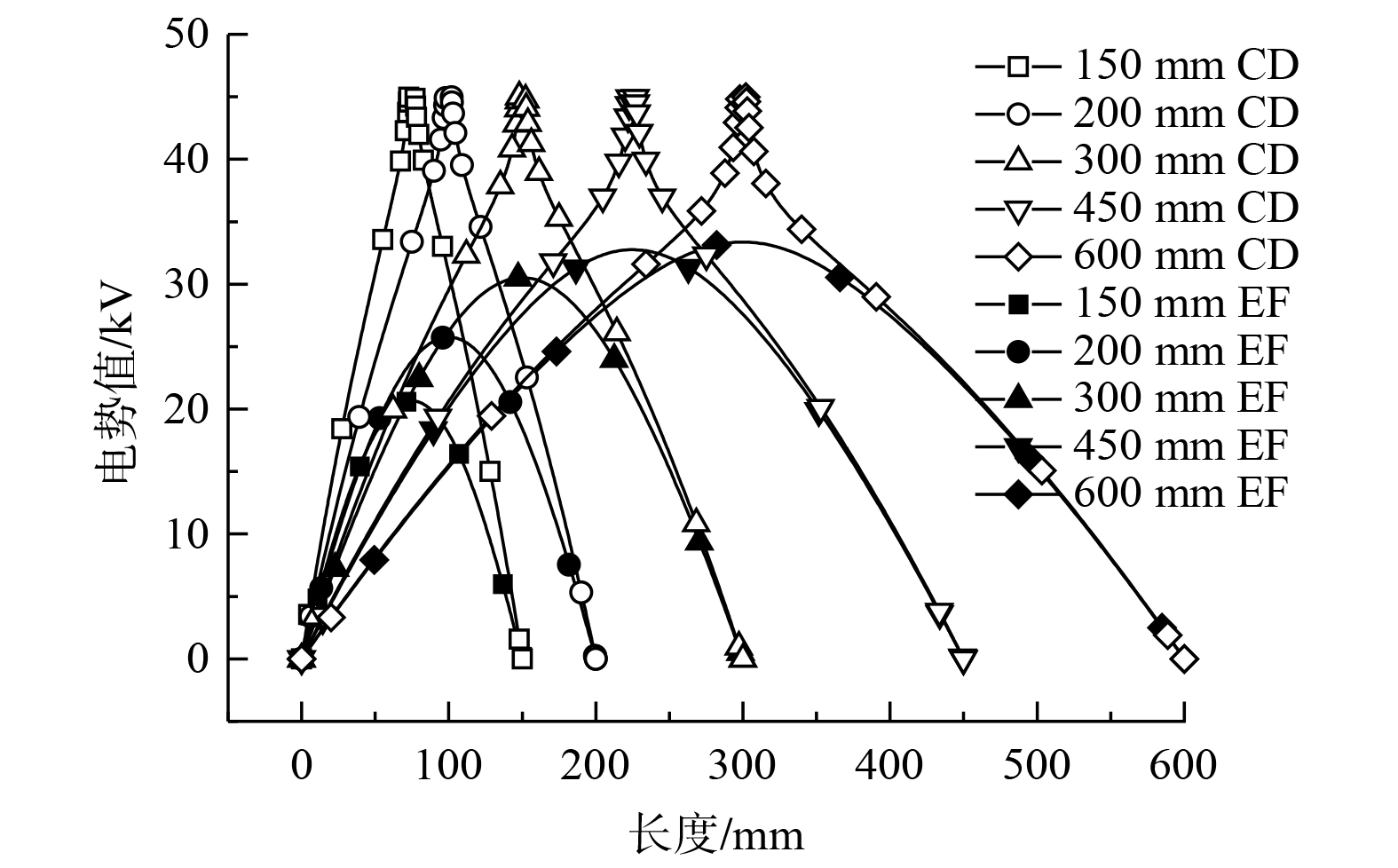
电势验证选用PENNEY[19]的线板式电除尘器实验数据进行验证，通过数值模拟软件建立1∶1的物理模型。在电场电压为28.7 kV、43.5 kV、46.5 kV的3种工况下，模拟收尘极板至第2根与第3根放电极中间 (即图1中ab线位置) 的电势值，并将模拟结果与实验数据进行对比，得出电势验证结果如图2所示，电势模拟结果与实验数据具有良好的拟合度。
-
静电除尘器内部流场实验数据选择KALLIO [20]的线板式电除尘器流场实验的数据，通过模拟计算进行风速验证。验证的实验工况：电场内3根放电极等距布置，电场电压为42 kV，入口风速分别为0.8 m·s−1、1.2 m·s−1、1.8 m·s−1时，模拟第1根电极至收尘极板 (即图1中cd线位置) 的风速值，模拟值与实验数据具有较高的一致性，如图3所示。
-
选择KIHM [21]的实验数据进行除尘效率的验证，实验模型参数：极板长度400 mm，板间距50 mm，8根放电极间距50 mm，入口风速2.0 m·s−1，颗粒粒径为4 μm。模拟不同电压下的除尘效率，模拟结果与实验数据对比如图4所示，当电压7.7 kV时，除尘效率相对误差最大，其值为5%。
综合电势、流场、除尘效率的验证结果，采用本文数学模型经COMSOL软件对静电除尘器性能进行数值模拟具有较高的可靠性，可以用于开展线板结构排布对电除尘性能影响的研究。
-
为研究线板结构排布对电除尘性能的影响趋势，分别设置2个实验组合，通过改变极板间距或极线间距，揭示其对除尘效率的影响规律。组合一几何模型如图5 (a) 所示：固定极线间距为180 mm，选择极板间距分别为150 mm、200 mm、300 mm、450 mm、600 mm下5种工况的模拟结果进行分析。组合二几何模型如图5 (b) 所示：固定极板间距为250 mm，选择极线间距分别为100 mm、150 mm、225 mm、300 mm、450 mm下5种工况的模拟结果进行分析。为了观测电场内部电势、空间电荷密度、风速、压力等参数的数据，设置4条观测线，如图5所示，其中AB线为穿过所有放电极且平行于极板的直线，CD线为穿过放电极且垂直于极板的直线，EF线位于两根放电极中间且垂直于极板的直线，GH线位于放电极与极板中间且平行于极板的直线。
对模型进行控制网格划分，网格总体大小设置细化网格，将电极附近网格进行加密，对边界网格设置了5层边界层和超细化网格，保证模型具有较高的单元网格质量，使模型具有较高的计算精度，几何模型网格划分如图6。
设定模型的参数，如表1所示。计算过程中，忽略温度、大气压力对除尘工况的影响，将入口风速、电场电压设置为定值，假设粉尘形状为球形颗粒物。收尘极板电势值设为零 (接地) ，通过记录总粒子数与出口壁面上的粒子数，得出除尘效率。模型的边界条件如表2所示。
-
1) 不同极板间距电势分布特征。在线板式电场内，放电极线上电势值为最大，收尘极板上电势为零，电势大小以电极线为圆心，向周围呈现发散式降低的分布趋势。如图7所示，随着极板间距变大，电场空间尺寸相应地增加，电势分布发生变化。从电极线至极板方向上电势的变化速率逐渐减小，电极线之间电势梯度随之降低，且电极线对附近电势的影响程度减轻。
在改变极板间距工况中，监测GH线上的电势值的变化。如图8所示，入口与出口处GH线上电势值随着极板间距增大而升高，而电极线位置处的电势峰值呈现下降趋势，且GH线上电势波动幅度随极板间距增大而降低。由于电场中极线与极板之间电势差为恒定值，故随着极板间距的增大，电极线至极板方向上的电势降低速率变缓，GH线上的电势值变化幅度明显降低，电势的变化趋势变缓。
在改变极板间距时，将CD线与EF线上的电势值变化联合考虑。如图9所示，电极线处电势最大值为45 kV，极板上电势值的最小值0 kV，在数值上与图7所呈现的趋势一致。随着极板间距的增大，CD、EF线上的电势值变化趋势逐渐变缓，且EF线上电势值的最大值逐渐升高，即两电极中间位置的电势值逐渐增大。
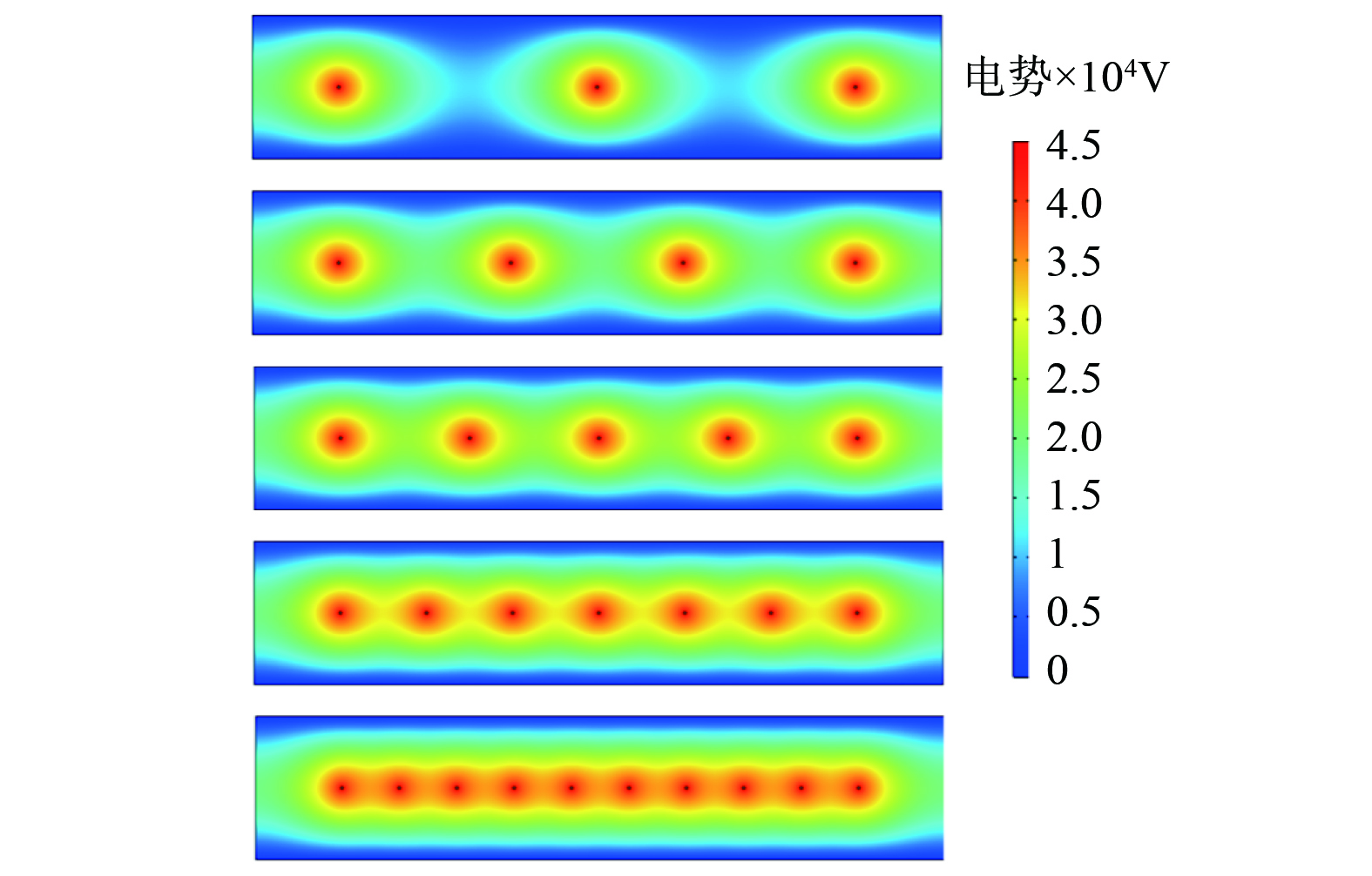
2) 不同极线间距电势分布特征。如图10所示，当极线间距减小时，单个电极产生电势的辐射范围发生了近距离重叠，电极之间的电势由点式分布呈现为条状分布，极线周围电势的影响程度增强，而电极至极板方向上电势分布没有发生明显变化。
通过监测AB线上的电势值变化，分析极线间距变化对电场电势值的影响趋势。如图11所示，随着极线间距减小，入口、出口处AB线上的电势值和电极处电势峰值保持不变，两电极之间的电势值逐渐增大，且电势值变化幅度逐渐降低，而两电极之间电势梯度基本不变。
电极线间距减小时，CD线上的电势值没有明显变化，而EF线上电势最大值逐渐升高，且EF线上数据变化速率也随之增大。如图12所示，CD线上电势变化表明，穿过电极线至极板方向上的电势大小不受极线间距的影响；EF线上电势呈现的趋势说明，两电极间距减小会引发两电极中间位置电势值的降低。
-
1) 极板间距对流场分布的影响。电场入口风速为1.0 m·s−1，当极板间距改变时，电场内部风流流动的雷诺数发生相应的变化。如图13所示，随着极板间距的增加，雷诺数变大，流场内产生的涡流的范围越小，流速分布更加均匀，电极对气流的扰动影响程度降低，流场较为稳定。
通过测量GH线上的风速变化，分析极板间距对风速的影响。如图14所示，极板间距为150 mm工况时，GH线上的风速波动幅度最大，流场风速最高值达1.21 m·s−1，此时GH线距离电极线较近，流动受到电极的影响较大。随着极板间距的增大，GH线上速度值浮动越小，当极板间距为600 mm时，GH线上的风速值波动较小，流场相对稳定。
2) 极线间距对流场分布的影响。如图15所示，当电极线数量较少时，电极彼此之间的影响较小，流场相对较为稳定；随着电极线数量增加，极线间距逐步减小，流场被隔离成两个流动通道，流动紊乱程度明显增大，流场内部速度波动较大，流速形成不均匀分布。
通过改变极线间距时，测量EF线上的风速变化。如图16所示，EF线上风速呈现倒双沟的形状，在两极线中间位置的风速最低；随着极线间距减小，EF线上风速有所增加；当极线间距为450 mm时，电极对EF线速度的影响较小，则风速值变化幅度相对最小，即极线间距越大，风速值改变的幅度越小。
-
粒径2.5 μm颗粒的运动轨迹如图17所示。颗粒在电场力的作用下，在运动过程中会向收尘极板移动，最终被收尘极板捕集，减小极板间距或极线间距，颗粒轨迹偏移的角度越大，颗粒的捕集效率越高，且颗粒在电场停留的时间越短；反之，随着极板间距或极线间距的增大，颗粒向极板偏移的角度越小，部分颗粒穿过出口直接逃逸。由于极线周围的高电势，颗粒在电极附近会有较高的速度值，随着距极线的距离越远，颗粒运动速度越小。所以，适当的控制极板间距或极线间距能够有效的提高除尘效率。
颗粒在模型中的能量密度如图18所示，电极线附近的粒子具有较大的能量密度，这是因为电极放电，空气被电离，粒子在电场内迅速荷电，从而获得电能，荷电后的粒子在电场力作用下运动向收尘极板，此时粒子具有较大的动能和电能。入口、出口处的粒子由于距离电极较远，则呈现出较低的能量密度；随着极板间距增大，电场内颗粒的能量密度逐渐降低；当极线间距减小时，由于电极彼此之间的相互影响，颗粒可以在电场中充分荷电，获得较多的能量，从而具有较高的能量密度。
-
在考虑不同的极板间距和极线间距对电场、流场性能的影响的同时，也探究了极板、极线间距对不同粒径颗粒的除尘效率的影响，选择颗粒的粒径分别为1 μm、2 μm、2.5 μm、3 μm、4 μm、5 μm进行模拟试验。如图19 (a) 所示，在极板间距和极线间距固定的情况下，颗粒粒径越大，捕集效率越高；颗粒粒度越小，捕集难度越高。对同一粒径的颗粒物，减小极板间距或极线间距促使颗粒除尘效率升高，然而，极板间距或极线间距的减小增加钢材使用成本和处理风量的降低，需要综合考虑。在组合一中，当极线间距为180 mm且极板间距为200 mm时，除尘效果最佳，对于粒径为2.5 μm的颗粒除尘效率达到98.6%。如图19 (b) 所示，当极板间距固定为250 mm时，对同一粒径的颗粒物，极线间距越大，颗粒除尘效率越低；当极线间距为225 mm时，对于粒径为3 μm的颗粒除尘效率达到95.2%。
-
1) 线板式电场电势呈现以电极线为圆心，向周围发散式降低的分布特征；随着极板间距变大，从电极线至极板方向电势的变化速率减小，电极线之间电势梯度随之降低；当极线间距减小时，电极之间的电势由点式分布呈现为条状分布，极线周围电势的影响程度增强。
2) 随着极板间距的增加，流场内产生的涡流的范围减小，电极对气流的扰动影响程度降低；当电极线数量增加时，极线间距减小，流场被隔离成类似两流动通道，流动紊乱程度明显增大，流场内部速度波动较大，流速形成不均匀分布。
3) 减小极板间距或极线间距，颗粒轨迹偏移的角度越大，颗粒的捕集效率越高，且颗粒在电场停留的时间越短；随着极板间距或极线间距增大，电场内颗粒的能量密度逐渐降低。
4) 颗粒粒径越大，除尘效率越高；极板间距或者极线间距越大，除尘效率越低。当极板间距为200 mm，且极线间距为180 mm时，对于粒径为2.5 μm的颗粒除尘效率达到98.6%。当极板间距为250 mm，且极线间距为225 mm时，对于粒径为3μm的颗粒除尘效率达到95.2%。
线板排布对静电除尘性能影响的数值模拟
Numerical simulation of the influence of wire and plate arrangement on electrostatic precipitator performance
-
摘要: 为揭示电极排布对线板式电除尘器除尘性能的影响规律，基于电晕电场模型、k-ε湍流模型、Lawless电荷累积模型，建立了电除尘多物理场模拟模型，并通过改变极板间距和极线间距，分析了电场电势、风速、颗粒运动轨迹、除尘效率的变化特征。结果表明：极板间距增大降低了电势变化速率，极线间距减小导致放电极电势分布由点式转为条状，极线周围电势影响程度增强；增加极板间距或极线间距，均能减小流场内涡流范围，提高流速分布的均匀性；极板间距或极线间距减小，颗粒轨迹偏移的角度增大，除尘效率随之升高，且颗粒在电场停留的时间缩短；除尘效率与颗粒粒径呈正相关，除尘效率与极板间距或极线间距呈负相关。模拟得到的优化工况为：当极线间距为180 mm、极板间距为200 mm时，电除尘器对粒径为2.5 μm的颗粒除尘效率为98.6%。本研究通过构建新的模拟模型应用于线板式电除尘器的工况优化中，可为电除尘器结构优化设计和性能提升提供参考。Abstract: In order to obtain the influence law of electrode arrangement on the performance of wire-plate electrostatic precipitator, the multi physical field simulation model was established based on corona electric field model, k-ε Turbulence model and Lawless model. The variation characteristics of electric field potential, wind speed, particle trajectory and dust removal efficiency were analyzed via changing the distance between plates or lines. The results showed that the increase of polar plate spacing reduced the potential change rate, and the decrease of polar line spacing led to the change of electrode potential distribution from point to strip, and the in-fluence degree of potential around electrode was enhanced. Increasing the distance between plates or lines could reduce the eddy current range and improve the uniformity of velocity distribution. With the decrease of polar plate spacing or polar line spacing, the angle of particle trajectory offset increased, and the dust removal efficiency increased. The dust removal efficiency was positively correlated with particle size, and negatively correlated with polar plate spacing or polar line spacing. When the polar line spacing was 180mm and the polar plate spacing was 200mm, the removal efficiency of particles with the size of 2.5μm was 98.6%. The research on the arrangement of wire plate structure can provide theoretical reference for the optimization of wire plate electrostatic precipitator.
-
甲基橙(methyl orange, MO)是一种水溶性偶氮染料，染料释放到天然水体中将严重影响水生生物生长，危害人类健康，具有致畸、致癌和致突变的作用[1]。MO在水中可电离为Na+与有机阴离子，并在微生物的作用下，产生芳香胺类中间体产物，随着食物链传播，在生物体内富集，加剧了人体健康的危害[2]。众所周知，塑料是一种可塑性强、化学稳定性高的高分子材料, 广泛应用于服装、包装、电子等各类产品中[3-6]。但是塑料的危害并没有引起人们的足够重视，80%的塑料产品没有经过有效处理就流入垃圾填埋场和自然环境中，并在重力作用、生物作用、水力作用、天气作用以及人类活动等外界驱动力的作用下，形成粒径＜5 mm 的微塑料[7]。微塑料具有不规则的表面结构、较大的比表面积以及对疏水性污染物较强的亲和力，使其能够作为环境污染物的载体，影响污染物在环境中的迁移转化[8-10]。
环境中的微塑料容易受到光照作用而发生老化，老化后的微塑料会产生新的含氧基团(如羟基、羰基等)，增加对有机污染物或重金属的吸附能力[11]。BHAGAT等[12]通过研究发现紫外(ultraviolet light, UV)老化增加了微塑料对有机污染物的亲和力；LI等[13]研究发现PE/PS/PA三种微塑料在UV老化后对Cr(VI)的吸附增强。但由于UV条件下微塑料老化速率较低，限制了人们研究微塑料在环境中与污染物的迁移转化。因此，关于微塑料的实验室加速老化技术逐渐被研究和开展。光催化技术是实验室加速微塑料老化的一种有效手段，常见的光催化剂有 TiO2、ZnO、Cds、H3BO3等，不同的光催化剂对PVC老化的影响如表1所示，其中 TiO2因具有活性高、热稳定性好、成本低等特点，使用最为广泛[14]，但TiO2光催化降解过程中光激发产生的电子-空穴对的复合会导致催化活性的降低。由于O3本身及其在水中分解产生的自由基具有一定的氧化能力，可以达到加速老化的目的[15-16]，因此将光催化和O3结合可以有效增强单一光催化技术的氧化能力，利用TiO2/UV协同老化过程中产生的 e−可与O3反应生成氧化性更强的·OH，抑制了电子-空穴对的复合，使光催化性能得到进一步提高[17]。综上所述，本文以PVC微塑料为研究对象，采用TiO2/UV/O3协同老化的方法对PVC进行加速老化实验，研究微塑料表面形貌及微观结构的变化，以及PVC对MO的吸附行为，为研究环境中的微塑料在污染物迁移转化过程中所起到的作用提供参考。
表 1 不同光催化剂对PVC的降解实例Table 1. Examples of degradation of microplastics by different photocatalysts催化剂 光源 光强/(mW·cm−2) 质量百分比/% 老化时间/h 质量 损失/% 参考文献 TiO2 254 nm 紫外光 1 1.5 250 52.8 [18] TiO2 254 nm 紫外光 1 2 216 35 [19] Cds 254 nm 紫外光 l 1.5 250 44.9 [18] Cds >300 nm 可见光 2 2 250 47.29 [18] H3BO3 >300 nm 可见光 2 2 250 14.9 [18] H3BO3 254 nm 紫外光 1 1.5 250 21.1 [18] ZnO 356 nm 紫外光 — — 2 20 [20] | Show Table
DownLoad:
CSV
1. 材料与方法
1.1 材料与仪器
实验材料微塑料聚氯乙烯(polyvinyl chloride, PVC, 300 μm)购自科信达建材有限公司，使用前将PVC置于1 L大烧杯中，加入无水乙醇漫过塑料超过1/4，磁力搅拌30 min，过滤后加入相同量的纯水搅拌均匀，重复上述操作3次滤干，在35 ℃下烘干备用。实验试剂包括二氧化钛、甲基橙(纯度>96%)、无水乙醇(AR)。
主要实验仪器：电子分析天平(JJ124B型，常熟市双杰测试仪器厂)；优普超纯水仪(UPHW-I-90T型，上海四科仪器设备有限公司)；磁力搅拌器(Feb-78-2型，江苏荣华仪器制造有限公司)；电热鼓风干燥箱(101-3A型，上海喆钛机械制造有限公司)；紫外灯(GGZ175-1型，上海季光特种照明电器厂)；恒温水浴搅拌器(SHA-C型，常州市金坛区指前镇旭日实验仪器厂)；循环水式多用真空泵(SHZ-D(Ⅲ)型，郑州科丰仪器设备有限公司)；低速台式离心机(TDL-4型，上海安亭科学仪器)；数控超声波冲洗器(KQ-50DB型，昆山市超声仪器有限公司)；臭氧机(CF-YG5型，北京山美水美环保高科技有限公司)。
1.2 老化塑料的制备
1) UV老化PVC 在UV光照下进行，将1 g微塑料样品加入1 L烧杯中搅拌均匀，加入一定量的纯水，用磁力搅拌器不间断搅拌保证微塑料和光催化剂在水体中充分接触。在室温下，于1×175 W紫外灯 (λ=365 nm) 下照射，期间每隔一定时间补充纯水。分别老化0.5、1、1.5和2 h后，超声离心30 min，将老化后的PVC进行抽滤，收集在9 mm的培养皿中，放入50 ℃烘箱中烘干备用，将样品分别编号为UV0.5-PVC，UV1-PVC，UV1.5-PVC，UV2-PVC。
2) UV/TiO2协同老化PVC 在UV光照下进行，将1 g微塑料样品和0.01 g TiO2光催化剂加入1 L烧杯中搅拌均匀,其余实验步骤与(1)UV老化相同，最后将样品分别编号为UV/T0.5-PVC，UV/T1-PVC,UV/T1.5-PVC，UV/T2-PVC。
3) TiO2/ UV /O3协同老化PVC 在UV光照下进行，将1 g微塑料样品和0.01 g TiO2光催化剂加入1 L烧杯中搅拌均匀，加入一定量的纯水，用磁力搅拌器不间断搅拌保证微塑料和光催化剂在水体中充分接触。在室温下，于1×175 W紫外灯 (λ=365 nm) 下照射，并在同一时刻通入5 L·min−1 的O3气体，其余实验步骤与(1)UV老化相同，最后将样品分别编号为O3-PVC-T0.5，O3-PVC-T1，O3-PVC-T1.5，O3-PVC-T2。
1.3 老化PVC的表征与分析
采用扫描电子显微镜(scanning electron microscope, SEM，FlexSEM 1 000，株式会社日立制作所)分析老化前后微塑料表面形貌特征变化；傅里叶变换红外光谱(Fourier transform infrared spectroscopy, FTIR ，Nicolet is50，美国赛默飞)鉴别不同体系老化前后官能团的变化；X射线衍射(X-ray diffractometer, XRD ，Smartlab SE，日本理学)在扫描范围2θ=10.0 °~60.0 °，扫描速度5.0 °·min−1，管电流 50 mA，管电压 40 kV下测定光催化老化微塑料PVC的晶型结构；纳米激光粒度Zeta电位仪(Zeta potential，Zetasizer Pro，马尔文帕纳科)在高稳定性He-Ne激光器，4 mW，632.8 nm条件下测定体系中微塑料的固-液界面电性，并对PVC在与不同光催化剂共存下老化0.5、1、1.5、2 h后的失重率进行分析。
1.4 老化微塑料吸附MO实验
1)吸附动力学实验: 称取0.1 g不同老化程度的PVC于50 mL锥形瓶中，加入30 mg·L−1 MO溶液30 mL，用玻璃盖密封瓶口进行吸附动力学实验。将样品置于(25±1) ℃，150 r·min−1恒温水浴振荡器中避光振荡(1、2、4、6、8、10、24、48、96 h)，静止5 min后，离心后进行抽滤，并用分光光度法测量滤液，每个实验组设置3个平行样，1个空白样。
2)吸附等温线实验: 准确称取0.1 g不同老化程度的PVC于50 mL锥形瓶中，分别加入质量浓度为10、20、30、50 mg·L−1 MO溶液30 mL并用玻璃盖密封。在恒温水浴振荡器中设置(25±1) ℃、150 r·min−1、避光条件下进行振荡48 h，离心后进行抽滤，并用分光光度法测量滤液，每个实验组设置3个平行样，1个空白样。
1.5 吸附机理实验及表征
分别称取0.1 g PVC和TiO2/ UV /O3协同老化2 h的PVC于50 mL锥形瓶中，加入30 mg·L−1 MO溶液30 mL，在恒温水浴振荡器中设置(25±1) ℃、150 r·min−1、避光条件下进行振荡48 h，在离心机中离心10 min(3 000 r·min−1),去除上清液，把吸附平衡后的微塑料干燥24 h。用玛瑙研钵充分研磨，采用Nicolet is50 傅里叶变换红外光谱仪测定，分辨率为4 cm−1，扫描范围为4 000~500 cm−1。
2. 结果与讨论
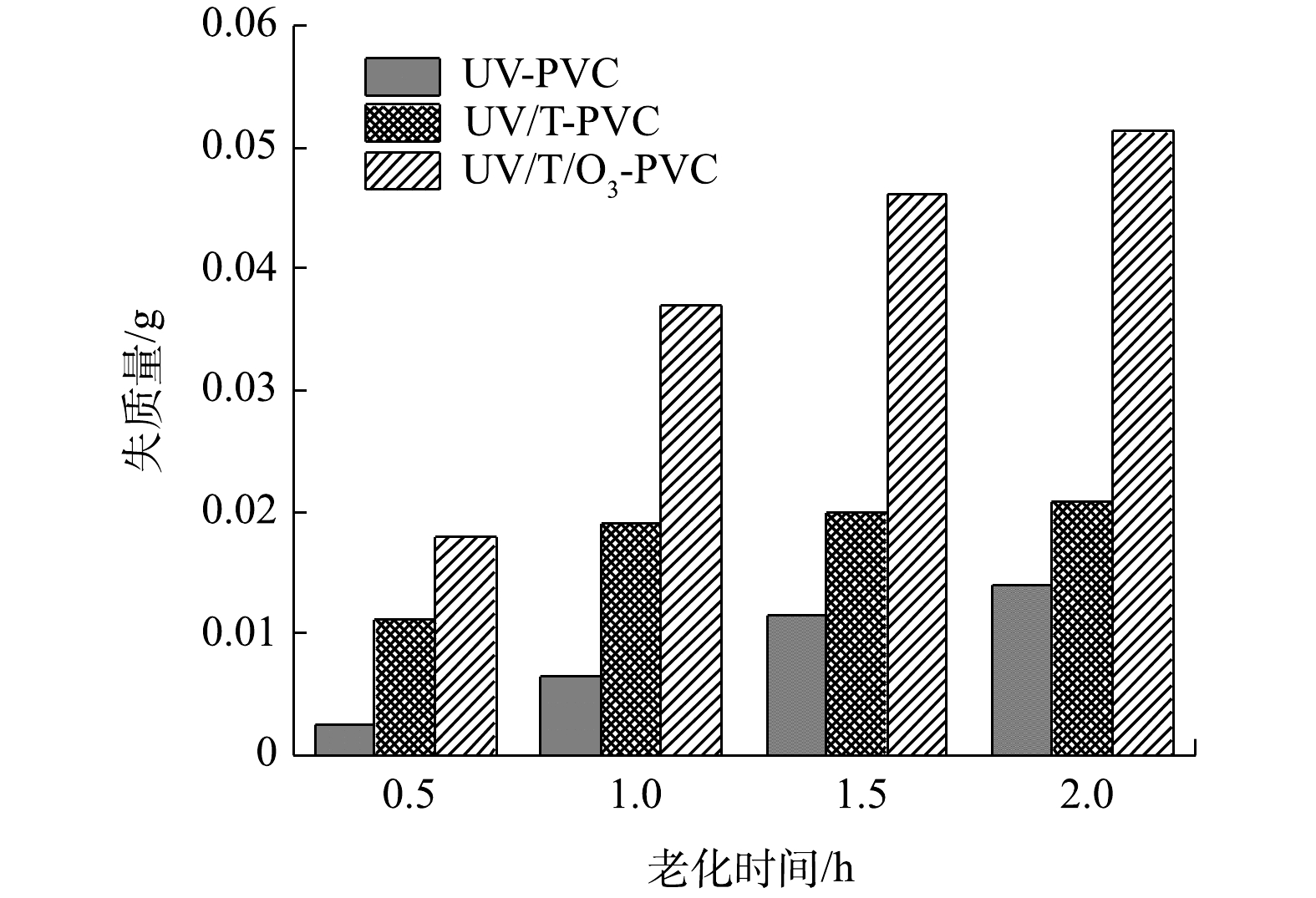
2.1 老化微塑料的质量分析
微塑料在老化过程中的重量变化可以直观的反映微塑料的老化程度。图1反映了UV老化PVC，TiO2/UV协同老化PVC，TiO2/ O3/UV协同老化PVC的质量损失情况。结果表明， TiO2/ O3/UV协同老化对PVC的老化效果最好，失质量均随着老化时间的增加而增加，不难推测，在阳光下使用较低数量的光催化剂亦可以有效地加速PVC的降解老化。在THOMAS[21]的研究中也证实了这一点，他通过将微塑料PE和TiO2制备成复合膜在高时效性的自然光照下老化，结果表明复合膜在老化后失重率为18.1%，相比于纯样微塑料0.5%是一个质的提升。
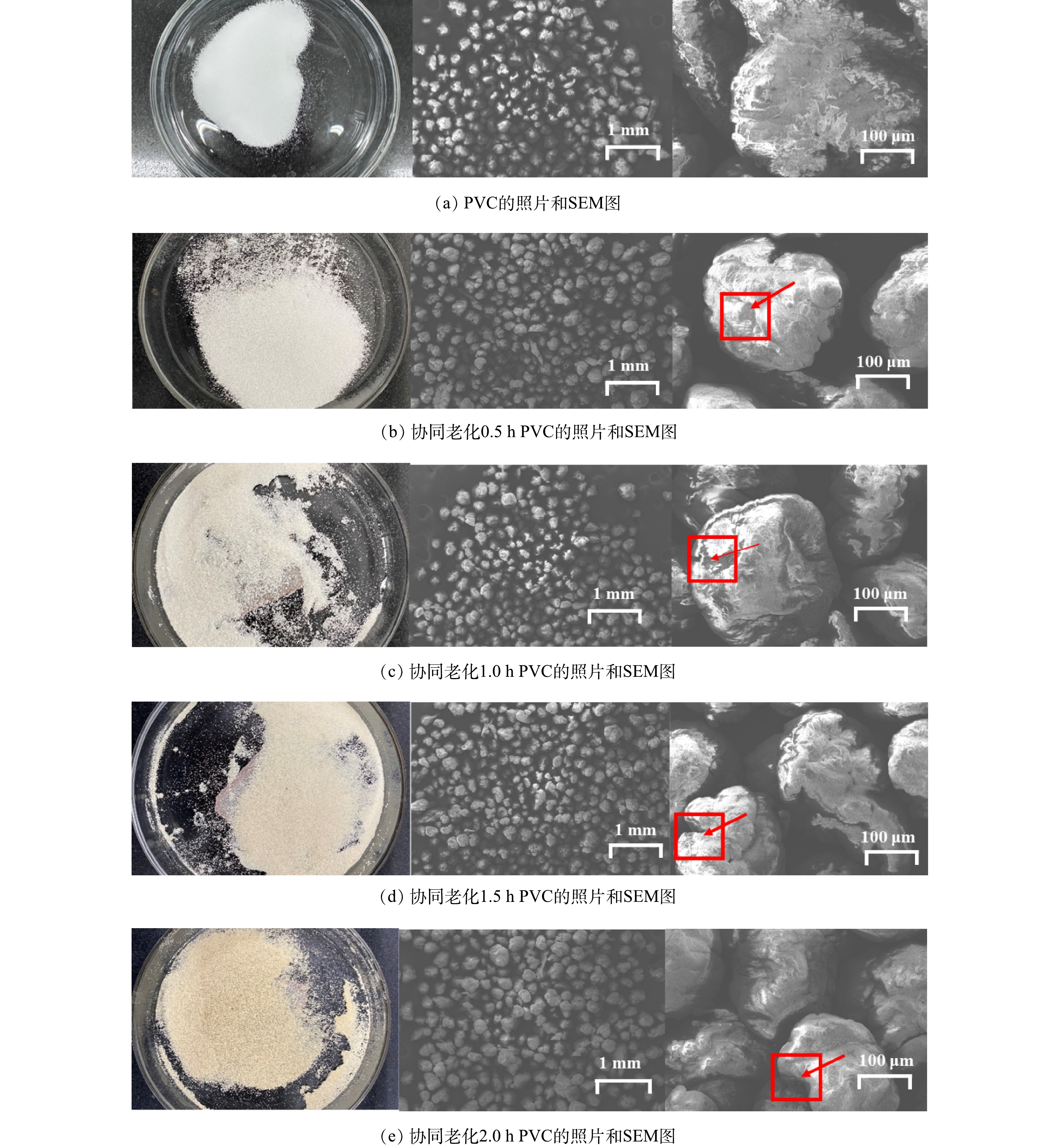
2.2 微塑料的形态特征
图2为PVC在介导二氧化钛下的协同老化不同时间的扫描电镜图。从图中可以看出未进行老化的原始PVC表面相对光滑，老化0.5 h的微塑料表面已经出现了明显的裂纹和凸起。伴随着老化时间的增加，老化程度逐渐加深，微塑料表面的褶皱相比单一光催化老化更加密集，颗粒的粒径也随着老化时间的增大而减小，老化后的PVC直径约为160~230 μm。同时，在图2中可以清晰的观察到老化后的PVC微塑料颜色由白色转变为黄色，这是由于多烯序列的形成(脱氢氯化反应)和随后的氧化(光漂白)之间的竞争引起的，式 (1)~(5) 表示了PVC在TiO2/UV/O3协同老化作用下产生自由基的过程[22]。
O3→TiO2(吸附) (1) TiO2+hv→TiO2+h++e−(2)e−+O3→O−3 (3) O−3+H+→HO3⋅ (4) HO3⋅→O2+⋅OH (5) 2.3 微塑料的晶体结构特征
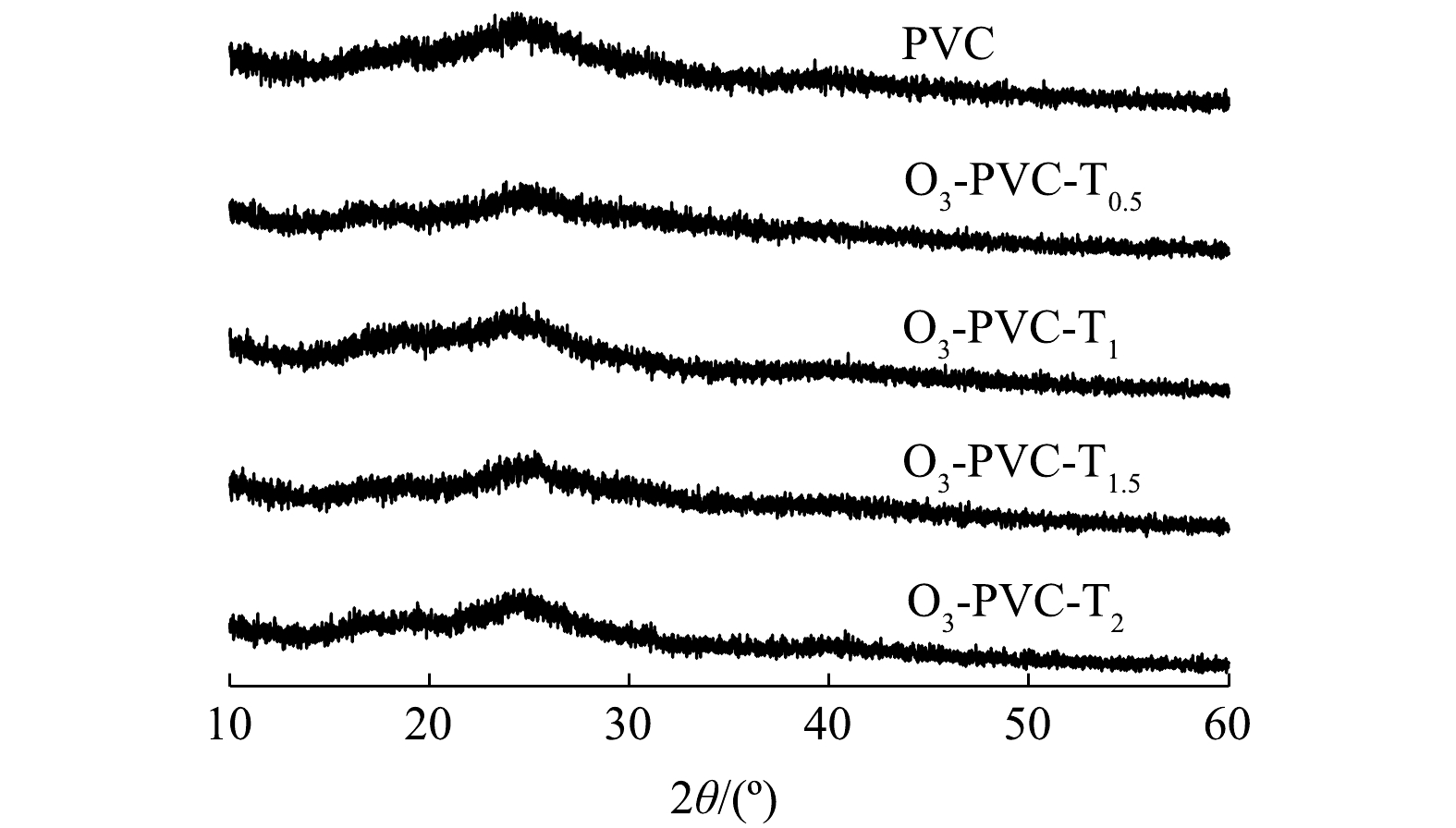
XRD可以反映聚合物表面晶相结构的比例，进一步分析光老化前后PVC的微观结构和结晶度，结果如图3所示。从图中可以看出，PVC 的 XRD 谱图呈弥散状态并未出现明显的结晶峰，表明 PVC 为非结晶性聚合物[23]。但与原始PVC相比，介导TiO2的光老化PVC在老化了不同时间后的吸收峰都有不同程度的降低，说明混合了TiO2的光老化实验会使PVC结晶度略有降低，这种现象可能是因为PVC表面部分官能团受到破坏以及新的官能团的产生。
2.4 微塑料红外图谱
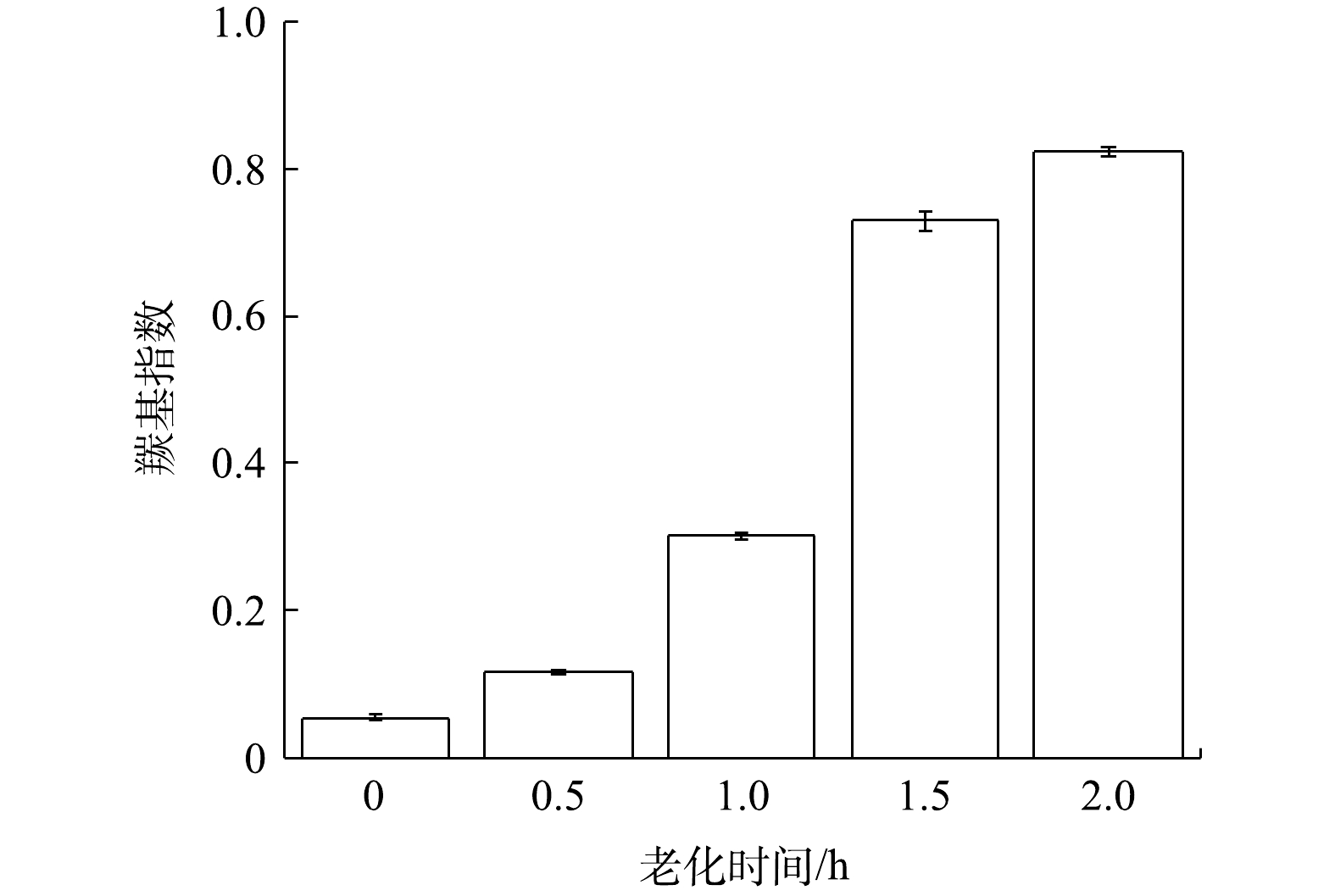
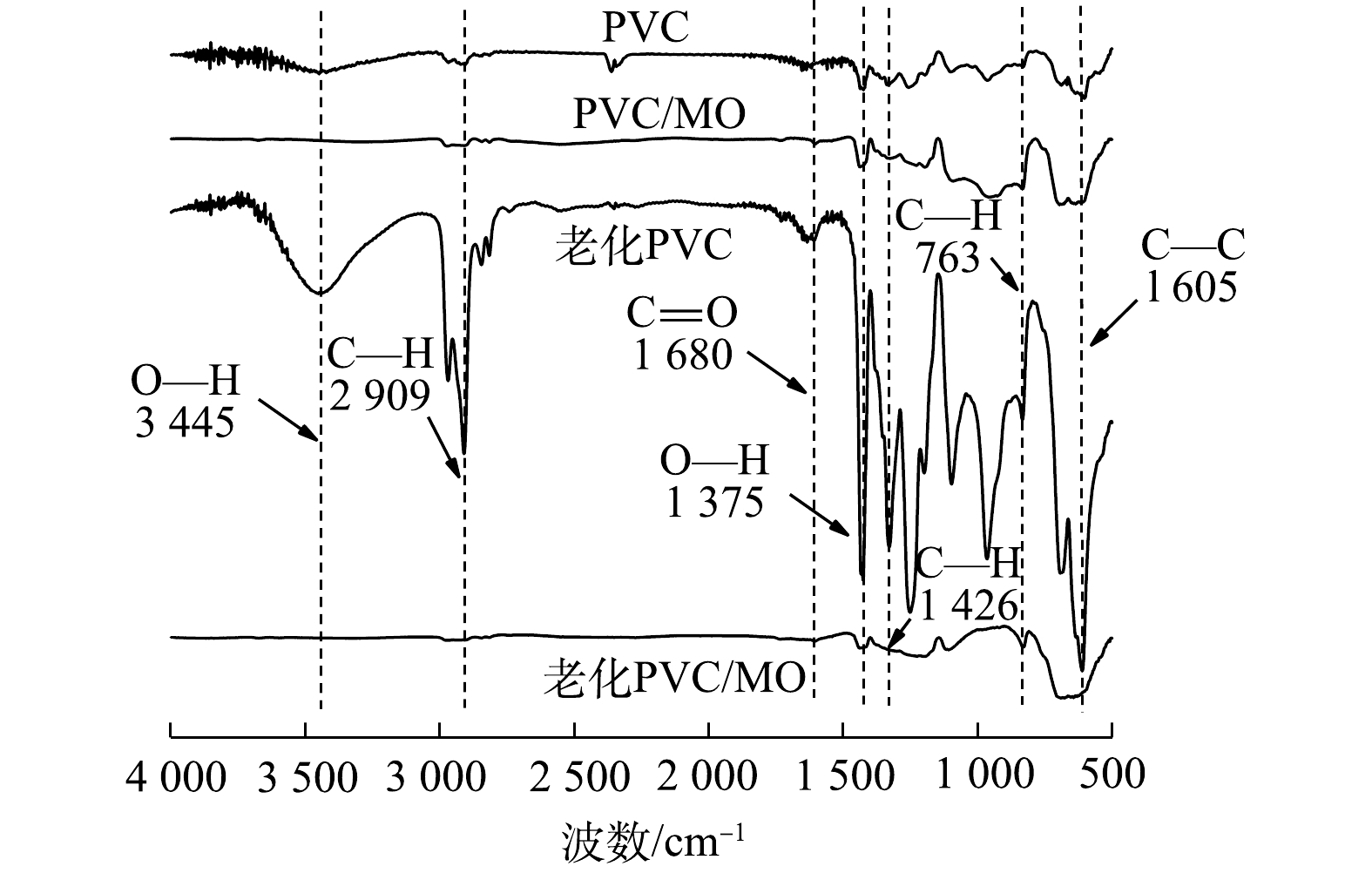
为了揭示TiO2和O3联合UV光照处理后PVC微塑料化学性质的变化，采用红外光谱法测定了微塑料官能团的变化。如图4所示，在1 736 cm−1(C=O)和3 445 cm−1(O-H)出现了两个额外的吸收带，对应于COOH基团的拉伸振动。这些变化反映了PVC微塑料在光老化作用下表面结构的变化。2 909 cm−1的吸收带强度属于CH2的不对称拉伸，此外1 250 cm−1~1 400 cm−1处的吸收带和605 cm−1处的峰值强度增大，这些分别是因为CH-Cl的拉伸振动和C-Cl的拉伸振动。这些变化均与PVC的氧化反应和脱氯反应相对应。推测可能是聚合物的骨架受到·OH的攻击而断裂，因此带有C=O和O-H基团的有机分子脱落，在PVC表面形成了含氧官能团[24]。通过羰基(1 736 cm−1)和碳氢键(2 909 cm−1)的吸收带来确定和量化PVC的联合光催化老化作用。微塑料PVC在TiO2/O3/UV联合作用下老化的羰基指数如图5所示，可以看出羰基指数同老化时间的变化呈现逐渐上升的趋势，这表明，在这段时间内，PVC的光氧化主要是由羟基而不是羰基副产物形成[25]。
2.5 微塑料的 Zeta电位表征
老化前后的PVC均带负电荷，由图6可见，PVC、O-PVC-T0.5、O-PVC-T1、O-PVC-T1.5和O-PVC-T2电位分别为−31.68、−19.73、−16.73、−4.62和−3.80 mV。与原始PVC相比，老化PVC的负电荷更低，这可以解释为光氧化过程后PVC表面形成的羰基[26]。Zeta电位也可用于预测粒子的稳定性或分散性，基于表面电荷，老化PVC比原始PVC显示出更低的稳定性，并且似乎更容易团聚[27]。随后，C=O的增加和C-H基团的减少以及负电荷的减少可能会改变老化PVC在溶液中的芳香性和稳定性。
图 6 老化前后PVC微塑料的Zeta电位变化Figure 6. Changes in Zeta potential of PVC microplastics before and after aging2.6 吸附动力学
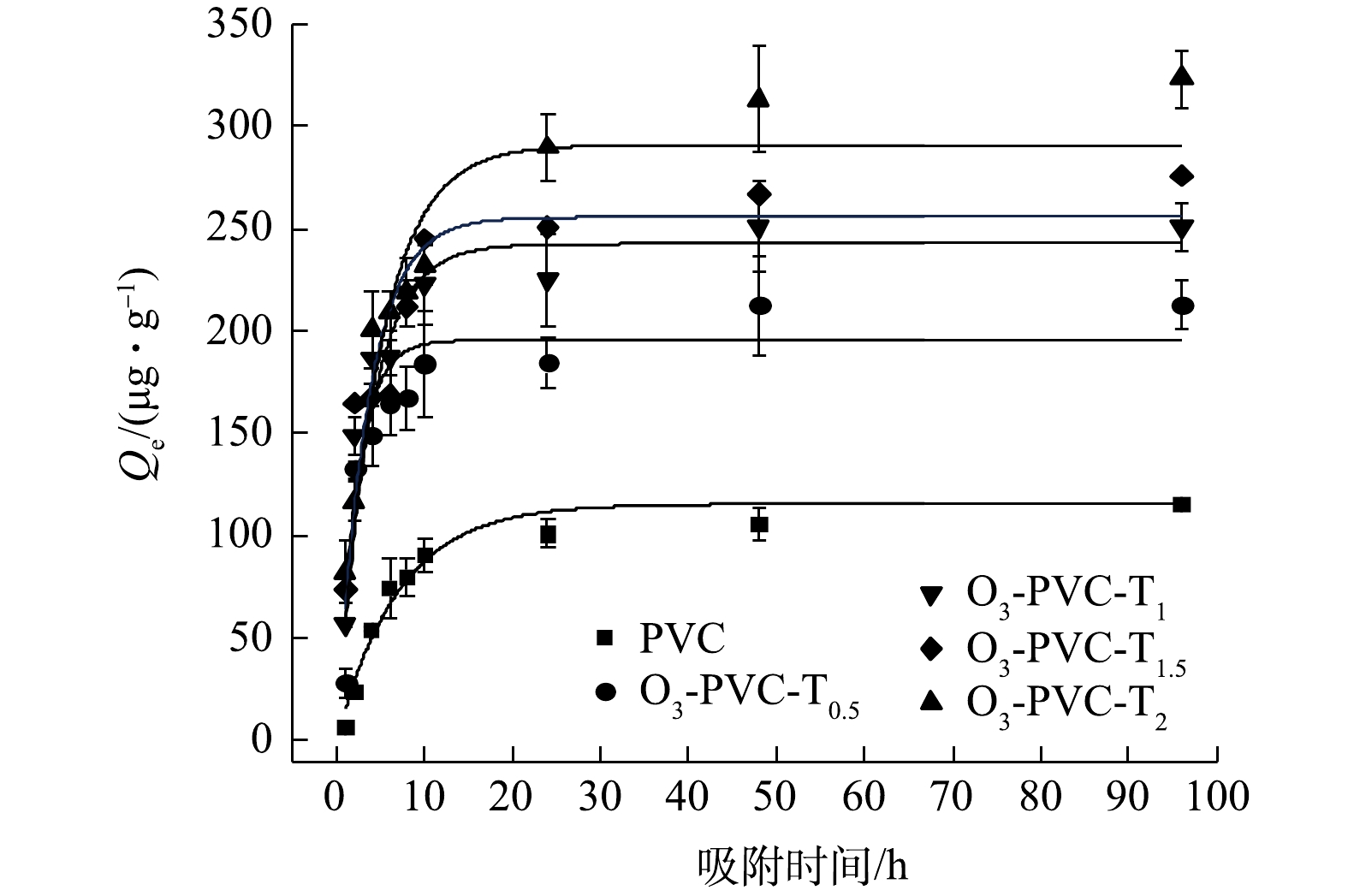
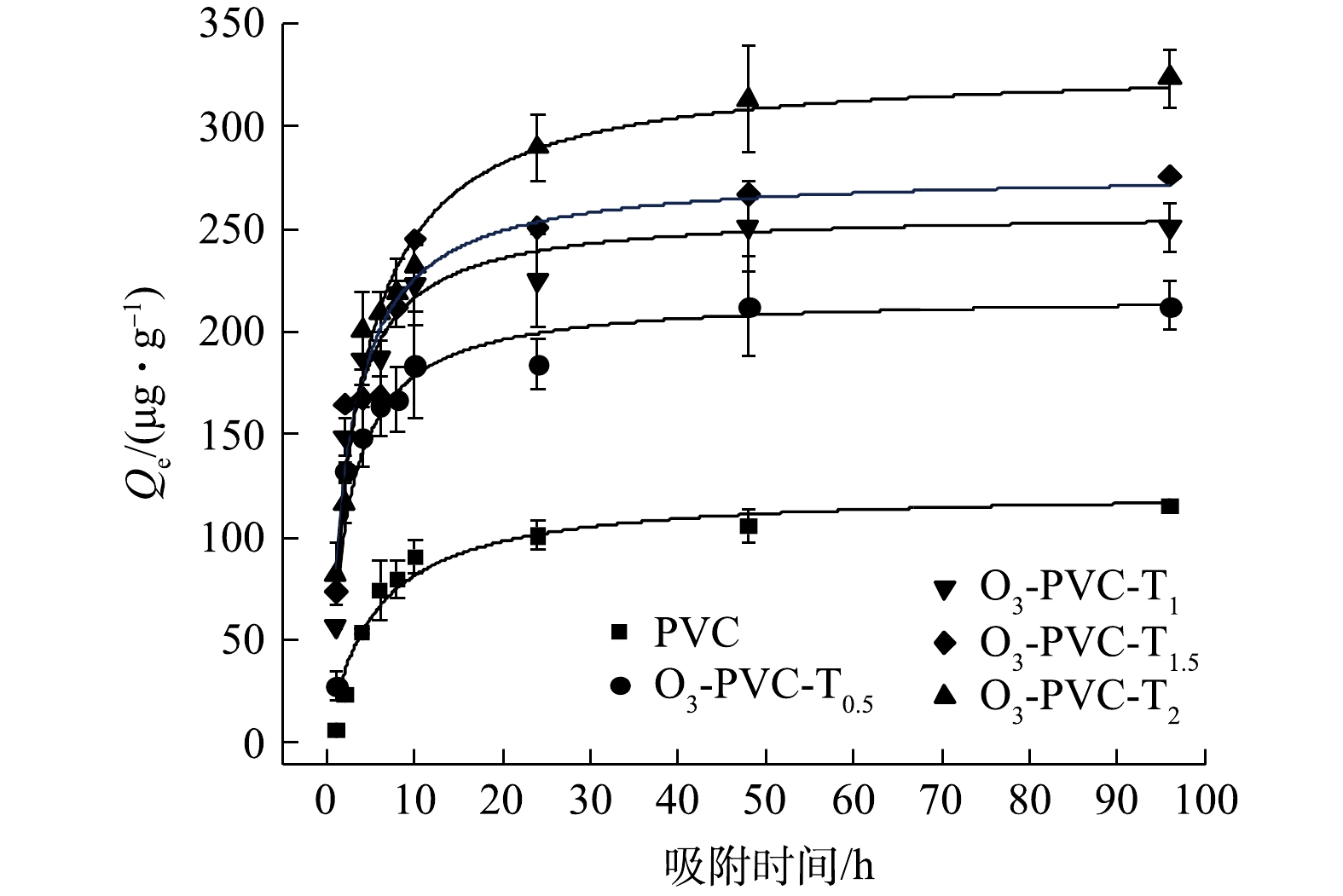
为进一步探讨联合老化PVC对MO吸附过程的影响，选取了老化程度较高的TiO2/O3/UV协同老化的PVC进行吸附MO的动力学实验。图7和图8为MO在老化前后PVC上的吸附动力学数据拟合结果。由图9可以看出，TiO2/O3/UV协同老化PVC颗粒对MO的吸附过程可以分为3个阶段，分别是快速吸附阶段、慢速吸附阶段和平衡阶段。在开始实验的6 h内，PVC对MO的吸附速度较快，吸附量可以达到各自平衡吸附量的75%左右，表明吸附初期的吸附速率较快，这可能与MPs水的初始浓度差带来的传质驱动力以及MPs表面存在大量的吸附位点有关；在之后的18 h内，老化前后的PVC对MO的吸附速率逐渐降低，吸附量略微增加步入缓慢吸附阶段；最终在48 h左右达到吸附平衡，这是因为两相的浓度差减小，MPs表面的吸附位点可能达到饱和[28-30]。此外，原始PVC和老化时间0.5、1、1.5、2 h的PVC的吸附量分别为115.522、212.314、250.798、275.791、323.091 ug·g−1，表明随着老化的持续进行，老化PVC的吸附能力呈现出递增的趋势。
图 7 老化前后PVC对MO的一级动力学Figure 7. Adsorption kinetics of MO on PVC before and after aging
图 8 老化前后PVC对MO的二级动力学Figure 8. Adsorption kinetics of MO on PVC before and after aging
图 9 颗粒扩散模型对老化前后PVC吸附MO的拟合Figure 9. Fitting of MO adsorption on PVC before and after aging by particle diffusion model为深入了解联合老化PVC对MO的吸附过程，分别采用拉格朗日准一级动力学模型、准二级动力学模型对吸附动力学数据进行拟合。表2总结了MO在老化前后PVC上吸附的2种动力学模型得出的参数。与准一级动力学模型相比(R2 > 0.775)，准二级动力学模型较好的描述了吸附过程，其拟合的相关系数值 R2 > 0.871，其得出的吸附量 qe值能够更好的与实验测量的qe值相吻合，表明化学吸附很可能是吸附过程中的限制步骤。
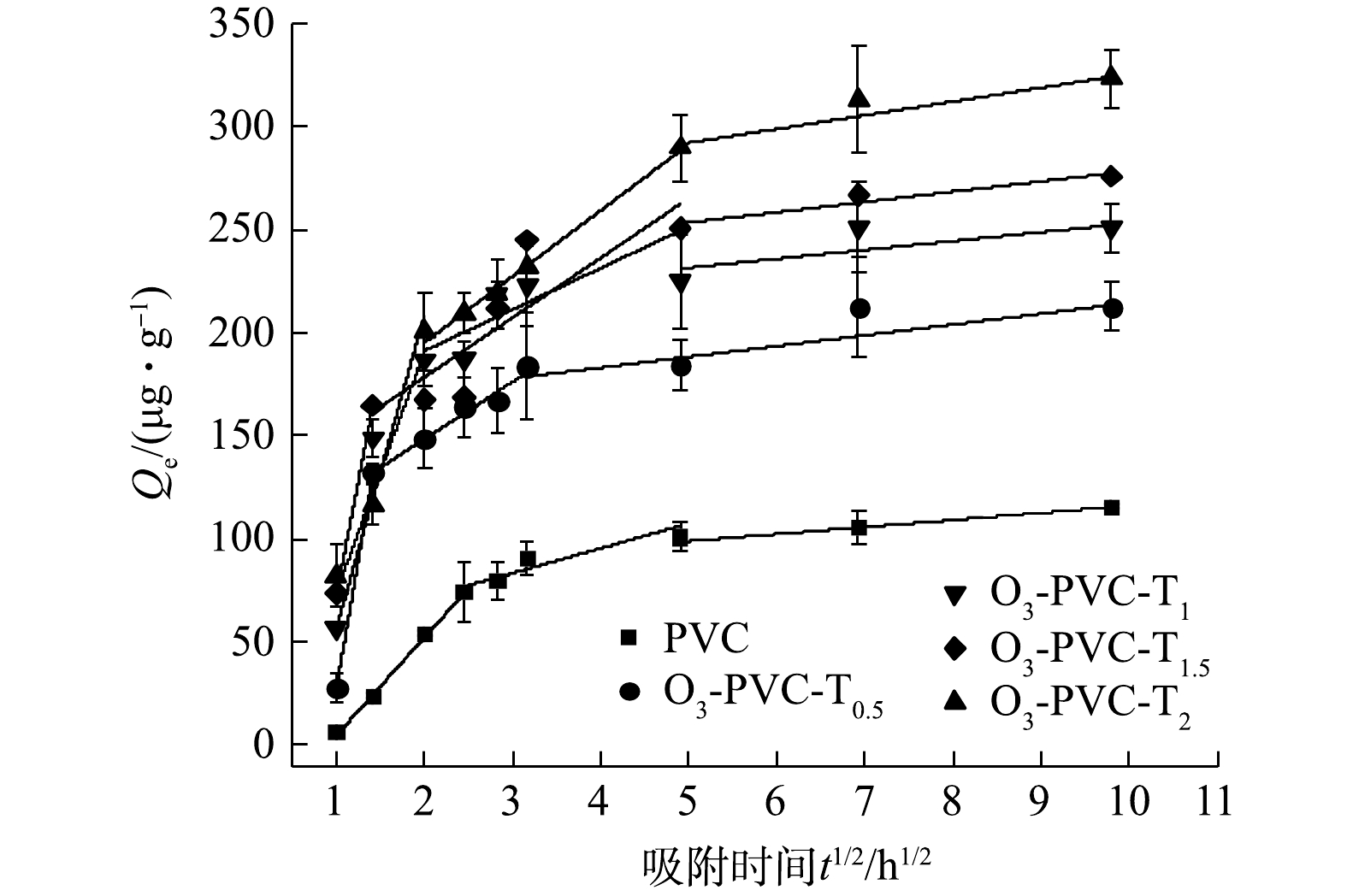
表 2 MO在老化前后PVC上的吸附动力学参数Table 2. Adsorption kinetics parameters of MO on PVC before and after aging样品 qe/(μg·g−1) 准一级动力学 准二级动力学 qe/(μg·g−1) K1 R2 qe/(μg·g−1) K2(×10−5) R2 PVC 115.522 115.455 0.143 0.989 122.886 161 0.948 O3-PVC-T0.5 212.314 195.531 0.454 0.775 217.416 211 0.871 O3-PVC-T1 250.798 242.483 0.275 0.972 258.5 200 0.927 O3-PVC-T1.5 275.791 255.491 0.289 0.813 277.505 158 0.902 O3-PVC-T2 323.091 290.845 0.217 0.907 329.7 89.726 0.979 | Show TableDownLoad:
CSV
采用颗粒内扩散模型，深入分析了吸附行为及控制过程的关键阶段，如传质、内部扩散和动态平衡。由图9可以看出，整个吸附过程并不呈线性变化，根据现有的研究方法可以将其分为0~6、6~24和24~96 h 3个阶段进行拟合，拟合参数如表3所示。可以看出，一开始的颗粒内扩散模型拟合表现出较好的线性关系(R12 > 0.870)，这一阶段主要为液膜扩散控制，反应速度快，发生外表面吸附，而第2阶段以颗粒内扩散为主，相互作用明显减弱，速率较慢( kw1>kw2)，第3阶段可能达到动态平衡过程[31]。由qe与t1/2的曲线不通过原点，可以推测吸附控制步骤同时受到外表面扩散和粒子内扩散的控制。从以上分析结果可以看出，MO在PVC上的吸附过程是一个非均匀扩散过程。在吸附过程的早期阶段，吸附过程主要由外表面的液膜扩散控制，而在后期阶段，颗粒内扩散过程发挥了重要作用[32]。然而，粒子内扩散步骤所需的时间取决于许多因素(如吸附剂粒径、温度、溶质浓度等)，并且难以控制或预测[33]。因此，通过人为划分吸附过程区间来确定kwi值可能存在一些偏差和不合理性。
表 3 MO在老化前后PVC上的内扩散模型参数Table 3. Internal diffusion model parameters of MO on PVC before and after aging样品 第1阶段 第2阶段 第3阶段 C1 Kw1 R12 C2 Kw2 R22 C3 Kw3 R32 PVC −45.69 49.65 0.99 56.48 9.20 0.82 84.85 3.13 0.98 O3−PVC-T0.5 −224.87 252.53 0.99 93.32 27.58 0.98 162.16 5.23 0.79 O3−PVC-T1 −146.8 220.33 0.99 120.69 28.91 0.69 228.49 4.99 0.87 O3−PVC-T1.5 −94.84 151.89 0.87 151.17 20.04 0.46 210 4.3 0.70 O3−PVC-T2 −42.77 116.78 0.92 131.35 32 0.99 258.75 6.68 0.91 | Show TableDownLoad:
CSV
2.7 吸附等温线
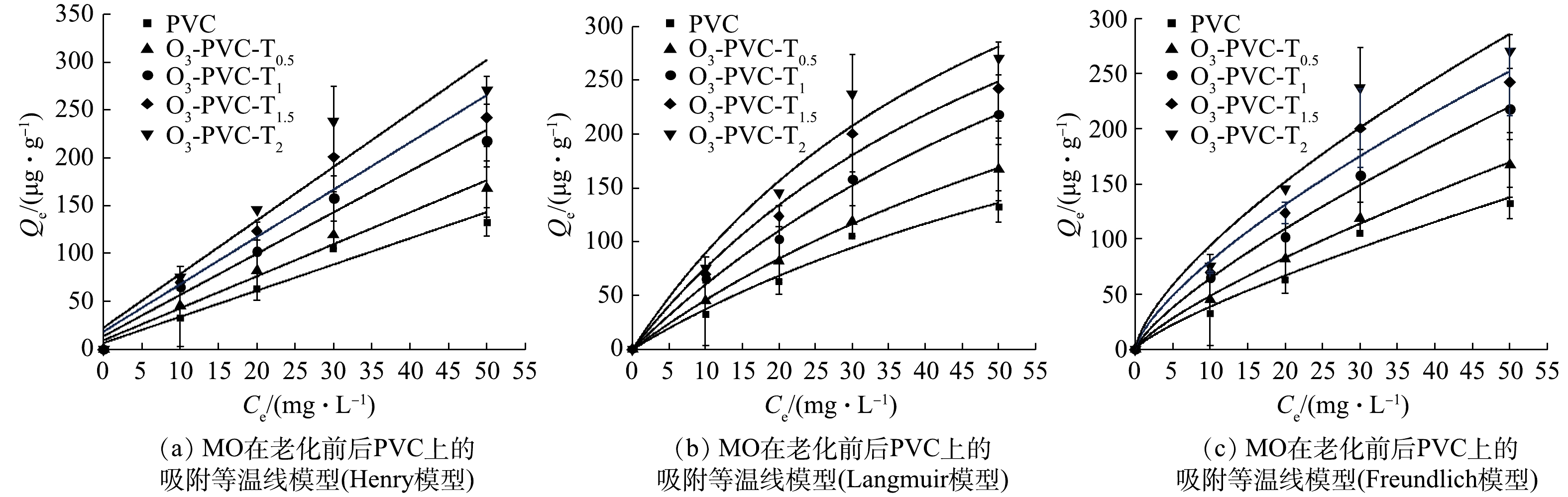
吸附等温线反映了吸附过程达到平衡时，吸附物分子在液相和固相之间的分布情况。本文采用Langmuir等温线、Freundlich等温线、Henry等温线来描述平衡吸附，结果如图10所示。Langmuir模型是一个非线性等温线，基于吸附和解吸与吸附剂表面积相关的模型，该模型认为吸附与吸附剂开放的表面积成正比，解吸与吸附剂覆盖的表面成正比。在这种情况下，吸附质分子的吸附发生在吸附剂的一个特定位点，而没有进一步的吸附发生在同一位点，适用于单分子层吸附。Freundlich模型，该模型建立在吸附过程发生在吸附剂的异质表面这一假说之上，适用于单分子层和多分子层[34]。Henry模型，在液相溶质平衡时，吸附剂中有机物的浓度和溶液中有机物的浓度成正比[35]。
图 10 MO在老化前后PVC上的吸附等温线模型Figure 10. Adsorption isotherm model of MO on PVC before and after aging表4列出了MO在TiO2/O3/UV联合老化不同处理时间下PVC上吸附得到的吸附等温线常数。由表4中可以看出，3种模型拟合的线性相关系数都较高，R2均大于0.90。其中，Langmuir等温线模型的线性回归系数R2大于0.914，低于Freundlich等温线模型 (R2>0.947~0.996)值最高。因此，Freundlich等温线能较好地拟合MO在PVC上的吸附，这表明MO和PVC之间的相互作用是在非均匀表面上的多层吸附，同时受到化学和物理吸附过程的影响，吸附机制主要以分配作用为主[36]。WU等[37]在研究中发现，5种双酚类物质在PVC上的吸附可以用Freundlich模型更好地描述。Freundlich模型的n值可以用来评估吸附效果和吸附过程，1/n表示浓度对吸附量影响的强弱。由表4中还可以看出，n在0.7~0.79，表明随着浓度的增加不同老化程度的PVC对MO的吸附量逐渐减小。这可能是由于在吸附过程中老化PVC的高能量吸附位点首先被占据，然后随着吸附的进行，低能吸附点位继续吸附MO。同时，随着老化时间的增加，KF逐渐增大，说明老化可以增强PVC对MO的亲和力。这可能是因为老化过程减少了PVC表面的负电荷，削弱了PVC和MO的静电斥力作用[36]。此外，结晶度对微塑料吸附的影响也是不可忽视的。GUO等[38] 在研究中发现不同PE颗粒对菲(phenanthrene)、林丹(lindane)、萘(naphthalene)的吸附随结晶度降低而增加。
表 4 老化前后的PVC对 MO的吸附等温线拟合参数表Table 4. The fitting parameters of PVC adsorption isotherm towards MO before and after aging样品 Henry Langmuir Freundlich Kd×10−3/(L·g−1) R2 Qm/(μg·g−1) KL R2 KF/(μg·g−1) n R2 PVC 6.601 0.948 401.811 0.010 0.952 6.268 0.790 0.969 O3-PVC-T0.5 3.338 0.976 506.753 0.010 0.989 8.031 0.780 0.996 O3-PVC-T1 4.306 0.971 579.578 0.015 0.949 11.069 0.764 0.993 O3-PVC-T1.5 4.934 0.928 604.564 0.017 0.914 15.421 0.715 0.968 O3-PVC-T2 5.587 0.900 633.214 0.011 0.947 19.181 0.691 0.987 | Show TableDownLoad:
CSV
2.8 吸附机理
从微塑料吸附MO前后的红外光谱图(图11)上可以明显看出，老化PVC吸附MO后表面发生了明显的结构的变化。老化PVC吸附MO后在 3 445cm–1和3 775 cm–1的O-H伸缩振动消失，在2 909、1 426、763 cm–1的C-H伸缩振动消失，在1 680 cm–1的C＝O伸缩振动消失，在605 cm–1处的C—Cl伸缩振动消失。进一步证实了，老化PVC对MO的吸附机理主要归因于羰基和羟基等含氧官能团增加，氢键作用及静电作用。
图 11 微塑料吸附MO前后红外光谱图Figure 11. Infrared spectra before and after adsorption of MO by microplastics3. 结论
1)经过TiO2/O3/UV联合老化后的PVC表面出现裂纹，羰基和羟基等含氧官能团有所增加，CI升高，Zeta电位值降低。
2)一级动力学模型可以较好地拟合PVC对MO的吸附过程，而老化过后PVC更适合二级动力学模型，吸附模式为液膜扩散和颗粒内扩散，老化前的PVC对MO的吸附以物理吸附为主，而老化后的PVC对MO的吸附以化学吸附为主。
3)老化前后的PVC均能与Freundlich等温线较好地拟合，MO与PVC之间的相互作用是在非均匀表面上的多层吸附，吸附机制主要以分配作用为主。
4)含氧官能团、氢键及静电作用对老化PVC的吸附性能有重要影响。相比原始 PVC，老化后的PVC对MO的吸附量增加了2~3倍，老化处理可增强PVC对共存污染物的运载能力。
-
图 2 不同电场电压下的电势模拟值与实验值拟合图
Figure 2. Fitting chart of simulated and experimental potential values under different electric field voltages
图 3 不同入口风速下的模拟值与实验值拟合图
Figure 3. Fitting chart of simulated and experimental values under different inlet speeds
图 4 不同电压下除尘效率的模拟值与实验值拟合图
Figure 4. Fitting chart of simulated and experimental values of dust removal efficiency under different voltages
图 7 不同极板间距电势分布云图
Figure 7. Cloud diagram of potential distribution at different polar plate spacing
图 8 不同极板间距GH线电势曲线
Figure 8. Potential curve of GH line at different polar plate spacing
图 9 不同极板间距CD线与EF线电势曲线
Figure 9. Potential curve of CD line and EF line at different polar plate spacing
图 10 不同极线间距电势分布云图
Figure 10. Cloud diagram of potential distribution at different polar line spacing
图 11 不同极线间距AB线电势曲线
Figure 11. Potential curve of AB line at different polar line spacing
图 12 不同极线间距CD线与EF线电势曲线
Figure 12. Potential curve of CD line and EF line at different polar line spacing
图 13 不同极板间距速度云图
Figure 13. Cloud diagram of velocity distribution at different polar plate spacing
图 14 不同极板间距GH线上风速曲线
Figure 14. Velocity curve of GH line at different polar plate spacing
图 15 不同极线间距速度云图
Figure 15. Cloud diagram of velocity distribution at different polar line spacing
图 16 不同极线间距EF线上风速曲线
Figure 16. Velocity curve of EF line at different polar line spacing
图 18 粉尘颗粒能量密度分布云图
Figure 18. Cloud diagram of energy density distribution of dust particles
图 19 极板间距和极线间距对除尘效率的影响
Figure 19. Influence of plate spacing and polar line spacing on dust removal efficiency
表 1 模型相关参数设置
Table 1. Setting of model related parameters
参数 数值 极板长度 1 200 mm 电极直径 2 mm 电极电压 45 kV 入口风速 1.0 m·s−1 空气温度 293.15 K 空气压力 101.3 kPa 颗粒直径 2.5 μm 颗粒密度 2 200 kg·m−1
下载: 导出CSV
-
[1] 刘学军, 胡汉芳, 郦建国, 等. 2020年电除尘行业发展评述和展望[J]. 中国环境产业, 2021, 3: 23-27. [2] 张金龙, 党小庆, 乐文毅, 等. 多孔收尘电极电场中荷电粒子的沉降规律及其除尘性能预测[J]. 环境工程学报, 2022, 16(05): 1589-1601. [3] 翁棣, 许冬冬, 张煜耀, 等. 高压静电除尘及伏安特性实验研究[J]. 实验技术与管理, 2019, 36(12): 52-56. [4] 张建平,高鹏飞,徐达成,等. 不同烟气流速下线板式电除尘器中磁场效应验证[J]. 环境工程学报, 2020, 14(11): 3121-3127. [5] 东明, 张宇轩, 李素芬, 等. 烟气流速对不同极线结构下静电除尘器内微细颗粒脱除的影响[J]. 热科学与技术, 2018, 17(1): 41-48. [6] 张哲, 李彩亭, 李珊红. 板式电除尘器多物理场耦合数值分析[J]. 环境科学与技术, 2019, 42(11): 187-192. [7] 裴艺凯, 杨振民, 黄超, 等. 电除尘器内部流动特性的数值模拟[J]. 应用能源技术, 2019, 263(11): 21-26. [8] 依成武, 刘诗雯, 史雪欣, 等. 单区式双涡旋型极板电除尘器除尘性能实验研究[J]. 高电压技术, 2016, 42(8): 2651-2658. [9] 胡建华, 李海燕. 电除尘器结构对除尘效率影响的数值分析[J]. 环境保护科学, 2018, 44(01): 83-88. [10] 张立莹, 雷洪, 牛宏, 等. 线板型静电除尘器的电场、流场与颗粒浓度分布的数值模拟[J]. 高电压技术, 2021, 47(11): 4144-4151. [11] 崔晓慧, 侯雪超, 张文婷, 等. 新型错位板对静电除尘器流场影响的数值模拟[J]. 环境工程学报, 2022, 16(01): 200-207. [12] AHMED K. Computation and measurement of corona current density and V-I characteristics in wires-to-plates electrostatic precipitator[J]. Journal of Electrostatics, 2016, 81: 1-8. doi: 10.1016/j.elstat.2016.02.005 [13] DONG M, ZHOU F, ZHANG Y X, et al. Numerical study on fine-particle charging and transport behaviour in electrostatic precipitators[J]. Powder Technology, 2018, 330: 210-218. doi: 10.1016/j.powtec.2018.02.038 [14] ARIF S, BRANKEN D J, EVERSON R C, et al. The influence of design parameters on the occurrence of shielding in multi-electrode ESPs and its effect on performance[J]. Journal of Electrostatics, 2018, 93: 17-30. doi: 10.1016/j.elstat.2018.03.001 [15] WANG Y F, ZHANG H, GAO W C, et al. Improving the removal of particles via electrostatic precipitator by optimizing the corona wire arrangement[J]. Powder Technology, 2021, 388: 201-211. doi: 10.1016/j.powtec.2021.04.087 [16] WANG X. Effects of corona wire distribution on characteristics of electrostatic precipitator[J]. Powder Technology, 2020, 366: 36-42. doi: 10.1016/j.powtec.2020.02.044 [17] 龙正伟, 冯壮波, 姚强. 静电除尘器数值模拟[J]. 化工学报, 2012, 63(11): 3393-3401. [18] LAWLESS P. A. Particle charging bounds, symmetry relations, and an analytic charging rate model for the continuum regime[J]. Journal of Aerosol Science, 1996, 27(2): 191-215. doi: 10.1016/0021-8502(95)00541-2 [19] PENNEY G W, MATICK R E. Potentials in D-C corona fields[J]. Transactions of the American Institute of Electrical Engineers, Part I:Communication and Electronics, 1960, 79(2): 91-99. doi: 10.1109/TCE.1960.6368550 [20] KALLIO G A, STOCK D E. Interaction of electrostatic and fluid dynamic fields in wire-plate precipitators[J]. Journal of Fluid Mechanics, 1992, 240: 133-166. doi: 10.1017/S0022112092000053 [21] KIHM K D. Effects of nonuniformities on particle transport in electrostatic[D]. Palo Alto : Stanford University, CA(USA), 1987. -
点击查看大图
计量
- 文章访问数: 5346
- HTML全文浏览数: 5346
- PDF下载数: 67
- 施引文献: 0
