-
氢氯氟烃 (HCFCs)曾被广泛地应用到空调、制冷、泡沫、气溶胶推进剂和阻燃剂等多个领域[1-2]. 因HCFCs会破坏臭氧层,被《蒙特利尔议定书》列为受控物质[3],所以一些化合物常被用来替代HCFCs[4],其中以氢氟烃类(HFCs)和氢氟烯烃类(HFOs)为代表化合物. 在过去几年中,这些替代物的排放量呈现快速增长的势头,并不断释放到大气中[4-5]. 为评估这些替代物是否为HCFCs的理想替代,在这些化合物进入大气对流层之前,需要充分了解其大气氧化机制的完整信息,尤其是大气持久性.
大气中的·OH具有强氧化性和低选择性,是很多污染物氧化降解的关键物种[6],因此污染物与·OH反应的二级反应速率常数(kOH, cm3·molecule−1·s−1)是评价污染物大气持久性的重要参数. 传统的kOH实验测定方法耗时耗力,亟待发展新的方法获取HFCs和HFOs的kOH. 近年来,计算机软件、硬件的飞速提升和量子化学理论的不断发展,尤其是密度泛函理论(DFT),可直接从分子结构出发实现kOH从头计算. 采用适当的量子化学计算方法不仅速度快而且结果可以媲美实验值,因此有望在kOH的快速获取方面发挥重要作用,从而有助于评估污染物的大气持久性. 近年来,探究·OH引发气相污染物降解的反应机制和动力学的研究逐渐增多,包括丙酸甲酯[7]、多氯联苯[8]、农药[9]等.
此外,也不乏利用量子化学方法探究HFCs和HFOs大气转化机制的研究,这些研究涉及M06-2X/6-311++G(df,p)//6-31+G(df,p)、MP2/cc-pVDZ、M11/6-311++G(d,p)等多种DFT方法,和过渡态理论(TST)、正则变分过渡态理论、变分过渡态理论等多种kOH计算方法[10-14]. 然而,目前量子化学计算的研究均以探究大气转化机制为主要目标,而kOH作为大气转化过程中的一个参数很少有人系统研究其计算方法. 这些研究使用的量子化学方法通常仅针对单个HFCs或HFOs,对其它HFCs或HFOs是否适用仍未可知.
本研究考察了碳链长度、官能团位置等因素,选择3个HFCs:1,1,1,2-四氟乙烷(CF3CFH2)、1,1,1,3,3,3-六氟丙烷(CF3CH2CF3)、2H,3H-十氟戊烷(C2F5(CHF)2CF3)和2个HFOs:1,1-二氟乙烯(CF2=CH2)、1H,1H,2H-十七氟-1-葵烯(CF3(CF2)7CH2=CH2)作为模型化合物,以其kOH实测值为参考,筛选适用于计算HFCs和HFOs气相kOH值的量子化学方法. 将不同的方法计算所得kOH与实测值进行比较,发展关于HFCs和HFOs的高准确性和适用性的kOH计算方法.
-
为使筛选的计算方法能够广泛应用于HFCs和HFOs的气相kOH计算,本研究从文献已报道kOH的HFCs和HFOs中,根据碳链长度和官能团位置的不同,筛选出CF3CFH2[15]、CF3CH2CF3[15]、C2F5(CHF)2CF3[16]共3个HFCs和CF2=CH2[17]、CF3(CF2)7CH2=CH2[18]共2个HFOs作为模型化合物,用于筛选合适的计算方法,其结构如图1所示.
-
由于在大气中HFCs和HFOs存在多种构象,不同构象与·OH的反应性不同,因此采用波恩奥本海默分子动力学(BOMD)[19]模拟和量子化学计算相结合的方法来获得目标化合物的最稳定构象. BOMD模拟使用CP2K 8.2.0[20]软件包,NVT系综,利用Nose-Hoover控温方法将温度稳定在300 K,利用BLYPD3/DZVP-GTH方法计算5000步,步长为0.5 fs. 从模拟的动力学轨迹中选取多种能量较低的构象,然后使用M06-2X[21]/cc-pVDZ[22]计算方法对结构进行优化,最终选取能量最低的构象作为目标化合物的最稳定构象,用来考察它与·OH的反应,最低能量构象如图1所示. 量子化学计算在Gaussian 09[23]软件包中进行.
-
M06-2X泛函已证明能够很好地用于研究氢夺取反应[21, 24],因此,本研究中所有反应涉及的反应物、反应前络合物、过渡态、反应后络合物和产物均采用M06-2X/cc-pVDZ计算水平进行结构优化. 此外,通过M06-2X/cc-pVDZ方法计算内禀反应坐标验证过渡态的准确性.
对于单点能的计算,选用2种能够考察色散作用的泛函(M06-2X-D3和ωB97X-D)[25]与8种3-zeta基组(aug-cc-pVTZ、may-cc-pVTZ、jun-cc-pVTZ、jul-cc-pVTZ、def2-TZVP、def2-TZVPP、pcseg-2和MG3S)[22, 26]进行组合,总计16种计算方法.
-
本研究采用TST[27]计算模型化合物的每条反应通道的kOH :
式中,κ代表隧道效应修正系数; σ代表反应简并度;h代表普朗克常数(6.626 × 10−34 J·s);T代表温度(K);kB代表玻尔兹曼常数(1.381 × 10−23 J·K−1);R代表摩尔气体常数(8.314 J·mol−1·K−1);P0代表大气压强(105 Pa);∆G‡,0代表标准活化自由能(kJ·mol−1),为过渡态吉布斯自由能减去反应物吉布斯自由能;对于双分子反应∆n为1,模型化合物HFCs和HFOs的kOH为此物质所有反应通道kOH之和.
对于κ的值,选择两种方法:(Wigner隧道效应校正系数(κW)[28]和Skodje-Truhlar隧道效应校正系数(κS)[29-30])进行计算,进而筛选出最合适的计算κ的方法.
κW的计算公式如下:
式中,υi†是TS的虚频(cm−1).
κS的计算方法如下:
当α > β时:
当α = β时:
当α < β时:
其中,∆V为势垒高度(kJ·mol−1),∆E为过渡态减去反应物的能量(kJ·mol−1),当∆E > 0 kJ·mol−1时,∆V为0 kJ·mol−1;反之,∆V为产物减去反应物的能量.
-
理论上,·OH与HFCs、HFOs可以发生夺H原子或F原子的反应,还可以在不饱和键发生·OH加成反应. 前人在研究CF2=C(CH3)CF3、CF2=C(CH3)2、1H-七氟环戊烯与·OH的反应中发现·OH难以夺取F原子[10, 13],因此本研究仅考虑·OH夺取HFCs和HFOs上的H原子. 对于3个HFCs,其反应机理仅为夺取C原子上的H原子. 由于H原子的位置可能会影响·OH夺取能力,所以选择CF3CFH2、CF3CH2CF3以及C2F5(CHF)2CF3作为模型化合物. 考虑到CF3CFH2最低构象具有Cs对称性,与·OH反应仅计算1条氢夺取途径. 而C2F5(CHF)2CF3和CF3CH2CF3分子的最低构象不具备对称性,需考虑所有的氢夺取反应途径. 对于HFOs,·OH与其反应机理包括H夺取和·OH加成. 考虑到CF2=CH2和CF3(CF2)7CH2=CH2分子的对称性,两者与·OH反应分别考虑3条(1条氢夺取+2条·OH加成)和6条(3条氢夺取+3条·OH加成)反应途径,所有模型化合物与·OH反应的反应途径见图2.
表1给出了在不同方法下计算的模型化合物的kOH值. 可以看出,CF3CF2H、 CF3CH2CF3、CF3CF2(CHF)2CF3、CF2CH2和CF3CH2CF3的kOH范围分别为6.79 × 10−16 — 4.93 × 10−14 cm3·molecule−1·s−1、8.47 × 10−17 — 5.99 × 10−15 cm3·molecule−1·s−1、2.10 × 10−15 — 5.65 × 10−14 cm3·molecule−1·s−1、4.81 × 10−13 — 8.90 × 10−11 cm3·molecule−1·s−1;7.27 × 10−14 — 1.08 × 10−11 cm3·molecule−1·s−1. 它们对应的大气半减期范围分别为:0.40 — 29.00 a;3.29 — 232.83 a;0.34 — 9.39 a;0.08 — 14.76 d;0.65 — 97.66 d. 表明不同计算方法对HFCs和HFOs的kOH值和持久性评估的影响较大. 此外,HFOs的kOH值普遍大于HFCs的kOH值的研究结果表明在对流层条件下,HFOs与·OH反应更快,更容易被·OH氧化去除.
-
表2列出了HFCs和HFOs实测与计算的lgkOH平均绝对误差(MAE),当MAE值小于0.500时认为方法预测的kOH的效果较好. 对于HFCs,ωB97X-D结合κS修正的TST的效果不理想(MAE的范围为0.692 — 1.003);M06-2X-D3结合κS修正的TST方法更具优势,其MAE值均小于0.250. 其中,采用基组def2-TZVP(MAE = 0.169)、may-cc-pVTZ (MAE = 0.170)、jun-cc-pVTZ (MAE = 0.178)、def2-TZVPP (MAE = 0.182)、jul-cc-pVTZ (MAE = 0.193)和aug-cc-pVTZ (MAE = 0.197)计算方法效果更优. 因此,当计算·OH和HFCs的反应时,建议使用上述修正TST和计算单点能的方法计算HFCs的kOH值. 对于HFOs,M06-2X-D3结合aug-cc-pVTZ基组计算单点能,并采用κW修正的TST计算kOH,得到的lgkOH的MAE最小(0.497). 因此,建议使用κW修正的TST方法结合M06-2X-D3/aug-cc-pVTZ//M06-2X/cc-pVDZ计算HFOs的kOH值.
对比所有模型化合物(3个HFCs和2个HFOs)lgkOH的MAE值,发现M06-2X-D3和ωB97X-D泛函结合不同基组得到的lgkOH的MAE范围分别为0.34—0.78和0.51—1.11. κS修正的TST方法结合M06-2X-D3泛函计算单点能的MAE值范围为0.34—0.50,均≤0.500. 按照MAE值排序,利用κS修正TST的动力学方法结合不同单点能计算方法中,最优的2种方法分别为结合M06-2X-D3/aug-cc-pVTZ (MAE = 0.34)和结合M06-2X-D3/jul-cc-pVTZ (MAE = 0.35). κW修正TST的动力学方法结合不同单点能计算方法中,最优的2种方法分别为结合M06-2X-D3/aug-cc-pVTZ (MAE = 0.47)和结合M06-2X-D3/jul-cc-pVTZ (MAE = 0.49). 因此,本研究推荐κS修正的M06-2X-D3/aug-cc-pVTZ//M06-2X/cc-pVDZ或者M06-2X-D3/jul-cc-pVTZ//M06-2X/cc-pVDZ方法计算HFCs和HFOs的kOH.
-
表3为筛选出分别适用于HCFs和HFOs的计算方法、计算得到的反应的热力学和动力学参数,其中HCFs的∆V均为0 kJ·mol−1. 对于3种HFCs,可以看出·OH 夺取HFCs上的H原子时,焓变(ΔH)均小于0 kJ·mol−1,表明反应可自发进行. 然而由于Δ E较高(12.75—23.16 kJ·mol−1),在298 K条件下反应很难发生. 表明HFCs可能在大气中持久存在. 此外,对比3种HFCs (CF3CH2F、CF3CH2CF3和CF3CF2(CHF)2CF3)的kOH值,可以看出碳链长度对HFCs的kOH几乎没有影响.
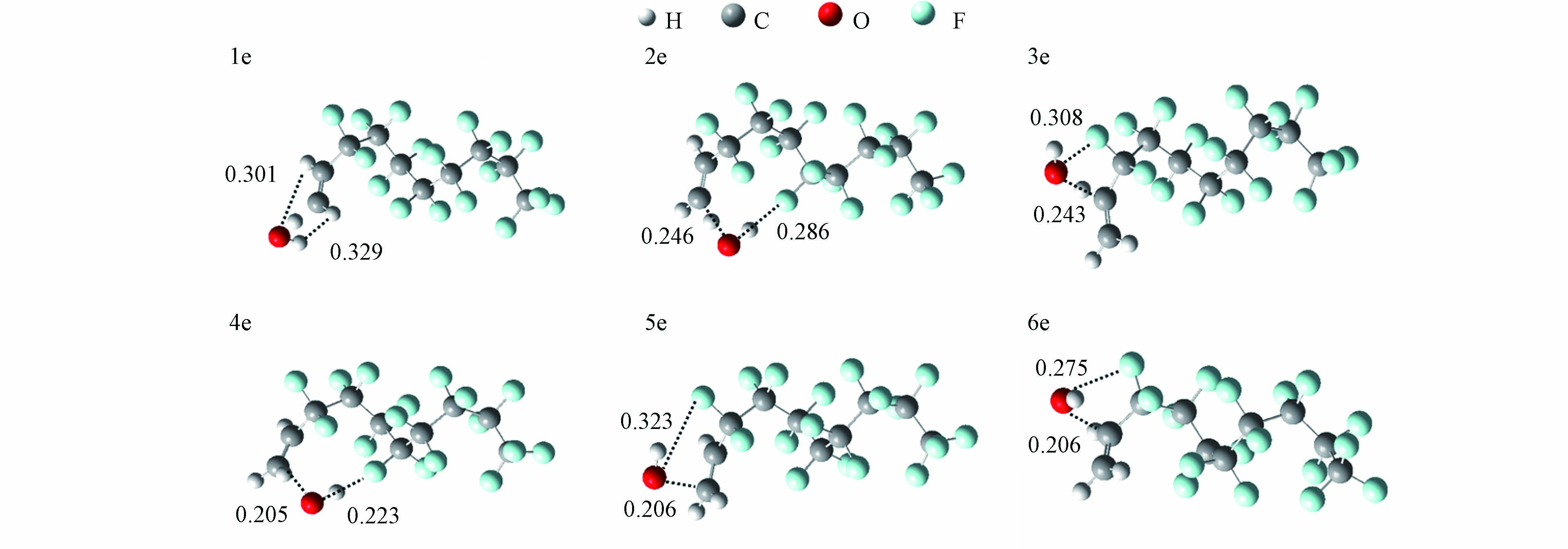
对于2种HFOs,可以看出所有反应的ΔH值小于0 kJ·mol−1,表明反应是放热反应. 而H夺取反应途径的ΔE值明显高于加成反应,表明·OH加成反应是·OH与2种HFOs反应的主要反应通道. 对比动力学数据,CF2=CH2和CF3(CF2)7CH2=CH2双键加成的产物分支比分别为99.99%和99.96%,同样证明双键加成是主要的反应机制. 此外,双键加成(3d, 4d)和(5d, 6d)反应通道的kOH值分别为3.76 × 10−13 cm3 ·molecule−1·s−1和4.00 × 10−13 cm3·molecule−1·s−1,说明—CF2和—CH2对kOH的影响较小. 值得注意的是,·OH加成到CF3(CF2)7CH2=CH2双键不同位置上时,其kOH的值也有明显不同. 5e的kOH为(1.74 × 10−13 cm3·molecule−1·s−1)明显高于4e (7.76 × 10−15 cm3·molecule−1·s−1)和6e (2.04 × 10−15 cm3·molecule−1·s−1)反应通道. 5e反应通道的产物分支比为94.62%,这表明·OH更容易与CF3(CF2)7CH2=CH2以5e的反应通道反应. 如图3中4e、5e和6e的过渡态所示,·OH在加成过程中,可能受到碳链上F原子空间位阻的影响.
-
本研究以5个HFCs、HFOs的kOH实测值作为参照,从16种单点能计算方法和2种动力学计算方法中筛选适合HFCs和HFOs的kOH值的热力学和动力学参数的计算方法. 以MAE作为检验计算方法效果的标准,HFCs推荐使用κS修正TST结合M06-2X-D3/def2-TZVP//M06-2X/cc-pVDZ方法计算kOH;HFOs推荐使用κW修正TST结合M06-2X-D3/aug-cc-pVTZ//M06-2X/cc-pVDZ方法计算kOH;推荐使用κS修正TST方法结合的M06-2X-D3/aug-cc-pVTZ//M06-2X/cc-pVDZ或M06-2X-D3/jul-cc-pVTZ//M06-2X/cc-pVDZ方法计算HFCs、HFOs的kOH. 此研究筛选了适用于计算HFCs和HFOs的kOH值的量子化学方法,为高效、准确预测HFCs和HFOs的kOH和评估其大气持久性提供了方法支撑.
气相氢氟烃和氢氟烯烃与·OH反应的量子化学计算方法筛选
Screening of quantum chemical method for the reactions of hydrofluorocarbons and hydrofluoroolefins with ·OH in the Atmosphere
-
摘要: 氢氟烃 (HFCs)和氢氟烯烃 (HFOs)常被用作氢氯氟烃的替代物. 为评估HFCs和HFOs是否可以理想替代氢氯氟烃,需要对其大气转化进行充分研究,尤其需要充分了解其大气持久性的信息. 目前用于评估化学品大气持久性的重要参数气相羟基自由基(·OH)二级反应速率常数(kOH)的数据量尚不能满足多种HFCs和HFOs的评估. 因此有必要发展能够快速预测kOH的方法. 量子化学计算方法具有高效、准确的优点,是预测kOH的重要手段. 然而目前研究使用的量子化学方法纷繁复杂,亟需筛选适合HFCs和HFOs的量子化学方法. 本研究基于3种HFCs(CF3CF2H、CF3CH2CF3和CF3CF2(CHF)2CF3)和2个HFOs(CF2CH2和CF3CH2CF3)的实验数据,从多种热力学参数计算方法和动力学计算方法中筛选适用于计算HFCs和HFOs气相kOH的方法. 研究结果表明,通过对比lgkOH的实测值与不同计算方法所得计算值之间的平均绝对误差(MAE),利用Skodje-Truhlar隧道效应校正系数 (κS)修正传统过渡态理论(TST),再结合M06-2X-D3/def2-TZVP//M06-2X/cc-pVDZ水平的密度泛函理论(DFT)计算HFCs的kOH效果最好,其MAE值为0.17;采用Wigner隧道效应校正系数 (κW)修正的TST结合M06-2X-D3/aug-cc-pVTZ//M06-2X/cc-pVDZ (MAE = 0.50)的方法计算HFOs的kOH效果最好;而κS修正TST的M06-2X-D3/aug-cc-pVTZ//M06-2X/cc-pVDZ (MAE = 0.34)或M06-2X-D3/jul-cc-pVTZ//M06-2X/cc-pVDZ (MAE = 0.35)方法都适用于计算HFCs和HFOs的kOH. 本研究筛选的方法为快速、准确计算HFCs和HFOs的kOH及评估其大气持久性提供了方法支撑.
-
关键词:
- 氢氟烃 (HFCs) /
- 氢氟烯烃 (HFOs) /
- ·OH /
- 量子化学计算 /
- 密度泛函理论(DFT) /
- 动力学.
Abstract: Hydrofluorocarbons (HFCs) and hydrofluoroolefins (HFOs) are mainly employed to substitute hydrochlorofluorocarbons. In order to evaluate whether the HFCs and HFOs are ideal alternatives for hydrochlorofluorocarbons or not, it is necessary to fully explore their atmospheric transformation, especially the information atmospheric persistence. To date, the quantity of second-order reaction rate constants (kOH) for chemicals reacting with hydroxyl radicals (·OH), which are essential parameters to characterize the atmospheric persistence of HFCs and HFOs, cannot meet the needs of atmospheric persistence assessment for HFCs and HFOs. Therefore, it is necessary to develop a method that can predict the kOH values efficiently. Considering the efficiency and accuracy of quantum chemical calculation, quantum chemical calculation is an important way to predict the kOH values. However, the quantum chemistry methods used in the current research are complex, and it is urgent to screen the quantum chemistry methods that are suitable for HFCs and HFOs. In this study, suitable methods for predicting the atmospheric kOH values of HFCs and HFOs were selected from a variety of thermodynamic parameter calculation methods and kinetics calculation methods based on the experimental data of 3 HFCs (CF3CF2H, CF3CH2CF3, and CF3CF2(CHF)2CF3) and 2 HFOs (CF2CH2 and CF3CH2CF3). The research results show that by comparing the mean absolute error (MAE) between the experimental lgkOH values and the lgkOH values calculated by different theoretical methods, the method employing the traditional transition state theory (TST) modified with the Skodje-Truhlar tunnel effect correction coefficient(κS) and combining with the density functional theory (DFT) at the M06-2X-D3/def2-TZVP//M06-2X/cc-pVDZ level has the best effect on calculating the kOH of HFCs accurately, whose MAE was 0.17; The method employing TST method modified with Wigner transmission coefficient (κW) and combining with the M06-2X-D3/aug-cc-pVTZ//M06-2X/cc-pVDZ (MAE= 0.50) showed the best performance for calculating the kOH values of HFOs; Both of the two methods that TST modified with the κW correction combine with M06-2X-D3/aug-cc-pVTZ//M06-2X/cc-pVDZ (MAE = 0.34) or M06-2X-D3/jul-cc-pVTZ//M06-2X/cc-pVDZ (MAE = 0.35) were suitable for the kOH prediction of HFCs and HFOs. In this study, the selected methods provide efficient and accurate methods for the kOH calculation and atmospheric persistence assessment of HFCs and HFOs. -
随着我国工业化水平以及人民生活水平的日益提高,恶臭气体带来的污染逐渐引起了全社会的重视. 我国《恶臭污染物排放标准》(GB 14554-93)中限制排放的恶臭污染物质包括硫化氢、甲硫醚、二甲二硫、甲硫醇、氨、二硫化碳、苯乙烯和三甲胺. 其中甲硫醇来源广泛,污水处理废气[1-2]、污泥处置废气[2-3]、垃圾填埋场废气[4-5]、制药厂废气[6]、造纸厂废气[7]、餐厨垃圾废气[8-9]、炼油废气[10-11]等主要恶臭成分中均含有甲硫醇. 其中,污水处理厂、垃圾填埋场、餐厨垃圾废气中的甲硫醇主要是由于蛋氨酸、甲硫氨酸、胱氨酸、半胱氨酸等含硫氨基酸的降解、巯基的转移以及含硫化合物的甲基化产生的. 甲硫醇是臭味最强的气体之一,其阈值仅为0.045 mg·m−3,且具有毒性和腐蚀性[12-13]. 此外,甲硫醇还属于含硫挥发性有机物,不但具有恶臭污染物的特征,而且具有挥发性有机物的特征[14],能够参与雾霾、光化学烟雾、二次气溶胶等环境污染事件的形成[15]. 因此,甲硫醇气体污染物的治理对我国经济高质量发展以及优美人居环境创建具有重要意义.
目前,广泛研究的甲硫醇治理技术主要包括吸附法[16-17]、生物法[18-19]、氧化法[12, 20]、等离子体法[21-22]、光催化法[23-24]、催化氧化法[13-14]和催化降解法[25-27]等. 其中氧化法和催化氧化法受到了人们的广泛关注,但由于甲硫醇氧化降解过程中生成的含硫化合物易使催化剂失活[13],实际应用过程中氧化法因其设备简单(喷淋洗涤塔、接触反应塔等)、氧化剂选择性多(臭氧、过氧化氢、次氯酸钠、高锰酸钾等)等特点而使用较为普遍,其中臭氧氧化法具有臭氧制备方便、均相反应效率高、脱臭效果好等优点而被广泛应用[28]. 虽然臭氧对甲硫醇臭气具有较好的脱臭效果,但关于臭氧投加剂量、反应条件等因素对甲硫醇去除效果的影响以及甲硫醇的臭氧氧化降解产物的研究鲜见报道. 因此,本文通过对臭氧投加量、接触反应时间、反应温度、湿度等因素的考察,并结合原位红外光谱、气相色谱-质谱联用和离子色谱技术研究了臭氧对甲硫醇的氧化降解性能及主要降解产物,以期为臭氧氧化法在甲硫醇脱臭净化领域的应用提供技术参考.
1. 材料与方法(Materials and methods)
1.1 仪器与试剂
甲硫醇标准气体(214.3 mg·m−3,大连大特气体有限公司);高纯氮气(纯度99.999%,郑州泽中科技有限公司);臭氧发生器(HK-10,郑州中仁臭氧技术服务有限公司);制氧机(IRC5PO2AW,Invacare,美国);加热磁力搅拌器(MR Hei-Tec,Heidolph,德国);所用其他试剂均为分析纯.
傅里叶变换红外光谱仪(Invenio S,Bruker,德国);气相色谱仪(GC2010,Shimadzu,日本);气体进样器(Acrichi OGS-11,北京聚芯追风科技有限公司);烟气分析仪(Testo 350,Testo,德国);总有机碳/总氮分析仪(Multi N/C 2100S,Analytikjena,德国);大气采样预浓缩进样系统(Entech7200,Entech,美国);气相色谱-质谱联用仪(7890B-7000D,Agilent,美国);臭氧浓度分析仪(UVOZ-1200:0—200 mg·L−1, 山东智普测控技术有限公司);质量流量控制器(CS200,北京七星华创电子股份有限公司);离子色谱仪(930,Metrohm,瑞士).
1.2 臭氧氧化甲硫醇实验
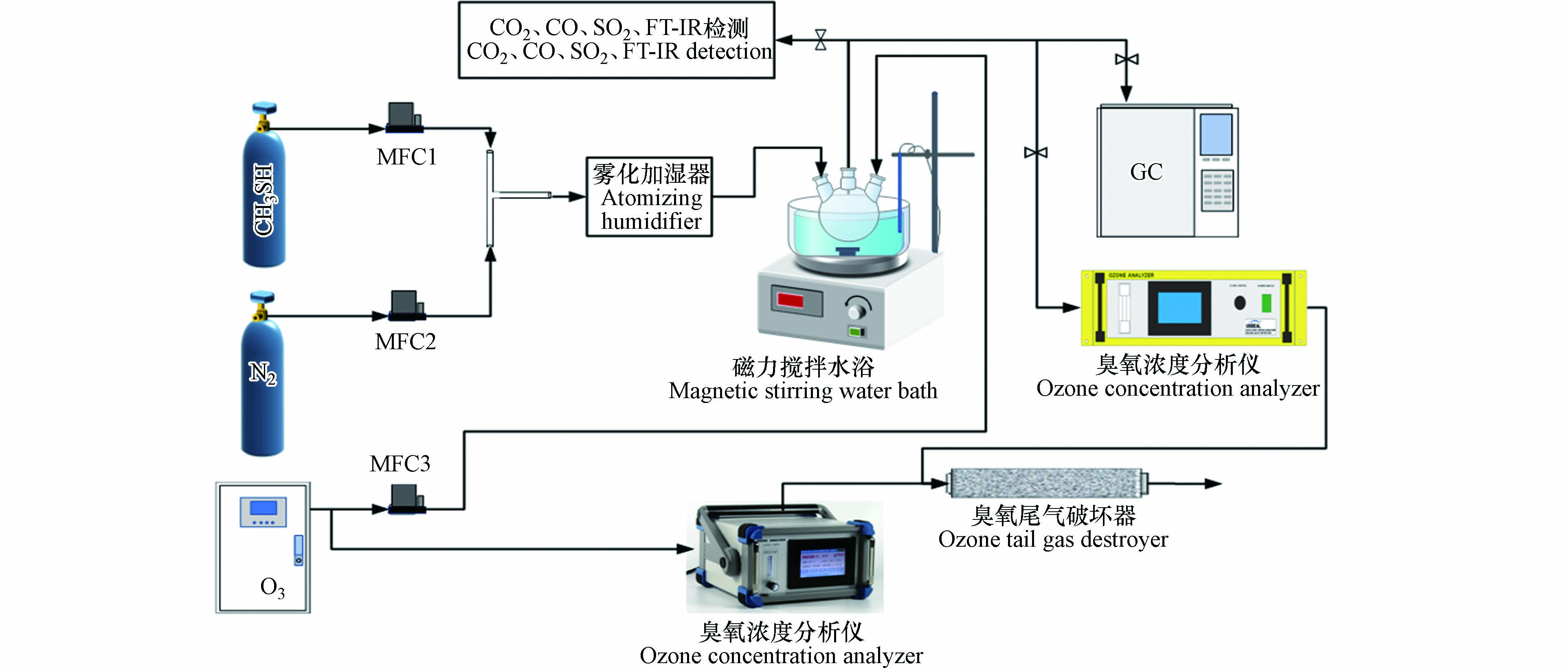
为了研究臭氧对甲硫醇的氧化降解性能,设计实验装置及工艺流程如图1所示. 根据所需甲硫醇和臭氧浓度计算甲硫醇、高纯N2和臭氧流量并通过质量流量控制器(MFC)进行调节控制,然后将磁力搅拌水浴调至需要的温度,臭氧与甲硫醇分别从两侧通入150 mL三颈烧瓶底部,并在三颈烧瓶中进行氧化反应,采用配备火焰光度检测器(FPD)的气相色谱仪进行定时采样监测甲硫醇、硫化氢、甲硫醚和二甲二硫浓度,每个条件采样测试3次并取平均值;同时,每次气体流程稳定后在线或使用聚四氟气体采样袋采样后进行SO2、CO2、CO浓度监测. 根据测得数据,分别按照式(1)和(2)计算甲硫醇去除率和二氧化碳选择性.
η=C0−C1C0×100% (1) SCO2=CCO2/C0×1.091×100% (2) 式中,η为甲硫醇去除率,%;C0为反应前气体中甲硫醇浓度,mg·m−3;C1为反应后气体中甲硫醇浓度,mg·m−3;
SCO2 CCO2 1.3 甲硫醇及其氧化降解产物分析
甲硫醇、二甲二硫、硫化氢等含硫化合物分析测试参照国标《空气质量硫化氢、甲硫醇、甲硫醚和二甲二硫的测定 气相色谱法》(GB/T 14678-93)方法并调整后测试,操作条件如下:岛津Rt-XLSulfur微填充柱,载气(N2)流速0.95 mL·min−1,进样量0.5 mL,气化室温度150 ℃,柱箱升温程序65—270 ℃(升温速率15 ℃·min−1,270 ℃保持10 min),FPD检测器温度280 ℃(H2:40 mL·min−1,空气:60 mL·min−1).
为了研究臭氧氧化降解甲硫醇过程中组分的变化,采用原位红外光谱分析技术对反应过程进行监测. 具体步骤为:(1)设置红外光谱仪为自动扫描模式,扫描间隔为1 min,红外光谱仪单次扫描条件为:扫描波数范围:4000—400 cm−1,分辨率4 cm−1,扫描次数32次;(2)采用高纯N2对硒化锌气体池(100 mL)进行置换;(3)用甲硫醇标准气体对硒化锌气体池中的高纯N2进行转换;(4)将气体池一端阀门打开,采用玻璃注射器从另一端阀门注入一定体积的臭氧,立即用红外光谱仪进行扫描测试.
参照国家环境保护标准《固定污染源废气甲硫醇等8种含硫有机化合物的测定 气袋采样-预浓缩/气相色谱-质谱法》(HJ 1078-2019)对甲硫醇的氧化降解产物进行分析,分析条件为:取样体积50.0 mL. 一级冷阱(空管):捕集温度:−30 ℃;捕集流速:80 mL·min−1;解析温度:10 ℃;阀温:120 ℃;烘烤温度:150 ℃;烘烤时间:10 min. 二级冷阱(TENAX管):捕集温度:−80 ℃;转移预热温度:−60 ℃;捕集流速:10 mL·min−1;解析温度:10 ℃;阀温:120 ℃;烘烤温度:190 ℃;烘烤时间:10 min. 三级冷阱(硅烷化不锈钢毛细管):聚焦温度:−170 ℃;解析时间:2 min;解析温度:50—70 ℃;烘烤时间:3 min. 色谱柱:安捷伦VF-1ms毛细管柱;柱箱升温程序:起始温度−35 ℃,保持 3 min 后以7.5 ℃·min−1 速度升温至180 ℃,保持3 min;进样口温度:100 ℃;溶剂延迟时间:2.7 min;载气流速:初始流速 2.5 mL·min−1,保持 4 min 后以 2 mL·min−1保持30 min;分流比:20:1. 质谱接口温度:250 ℃;离子源温度:230 ℃;离子化能量:70 eV;扫描方式:全扫描(SCAN);扫描范围:35—300 amu.
采用总有机碳/总氮分析仪进行二氧化碳浓度检测:气体六通阀进样,定量环体积40 mL,根据测得的碳含量计算二氧化碳浓度.
参照国家环境保护标准《环境空气总烃、甲烷和非甲烷总烃的测定 直接进样-气相色谱法》(HJ 604-2017)分析净化气中甲烷含量,分析条件为:GDX-502填充柱(3 m×3 mm),进样口温度:100 ℃,柱温80 ℃,柱流量10 mL·min−1,FID检测器(H2:30 mL·min−1,空气:300 mL·min−1).
参照文献[29]测试净化气中硫氧化物含量,具体步骤如下:移取0.01 mol· L−1 NaOH溶液10 mL于多孔玻板吸收管中,将净化气持续通入多孔玻板吸收管中,直到总吸收气体体积达到2 L,停止通气,移出吸收液,采用离子色谱仪进行分析测试.
2. 结果与讨论(Results and discussion)
2.1 氧气对甲硫醇的氧化
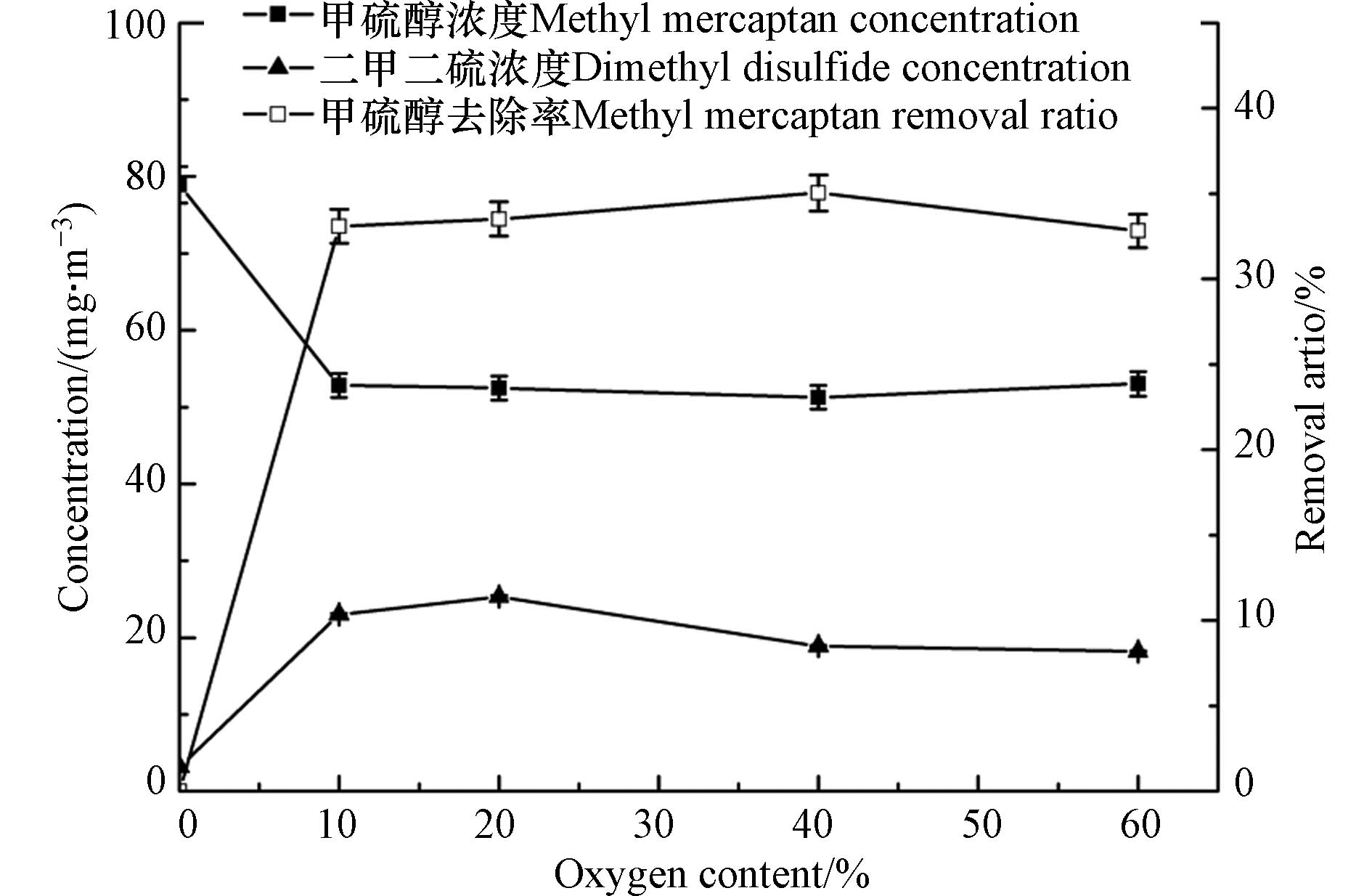
甲硫醇为还原性含硫化合物,浓度较高时会被氧气氧化,为了更客观地研究并评价臭氧对甲硫醇的氧化降解性能,该研究首先考察了氧气对甲硫醇的氧化性能,结果见图2. 由图2可以看出,对于初始浓度为78.9 mg·m−3的甲硫醇气体,氧气可将甲硫醇部分氧化去除,其主要氧化产物为二甲二硫,但其氧化效果有限,甲硫醇的去除率最高仅为28%,且当氧含量高于10%时,甲硫醇的去除率不再随氧含量的增大而变化;由于实际应用场景尤其是污水处理厂、垃圾填埋场等恶臭气体排放场景中均为空气背景,其氧含量为21%左右,因此,本研究在后续实验中均将氧含量调至21%左右.
2.2 臭氧投加量的影响
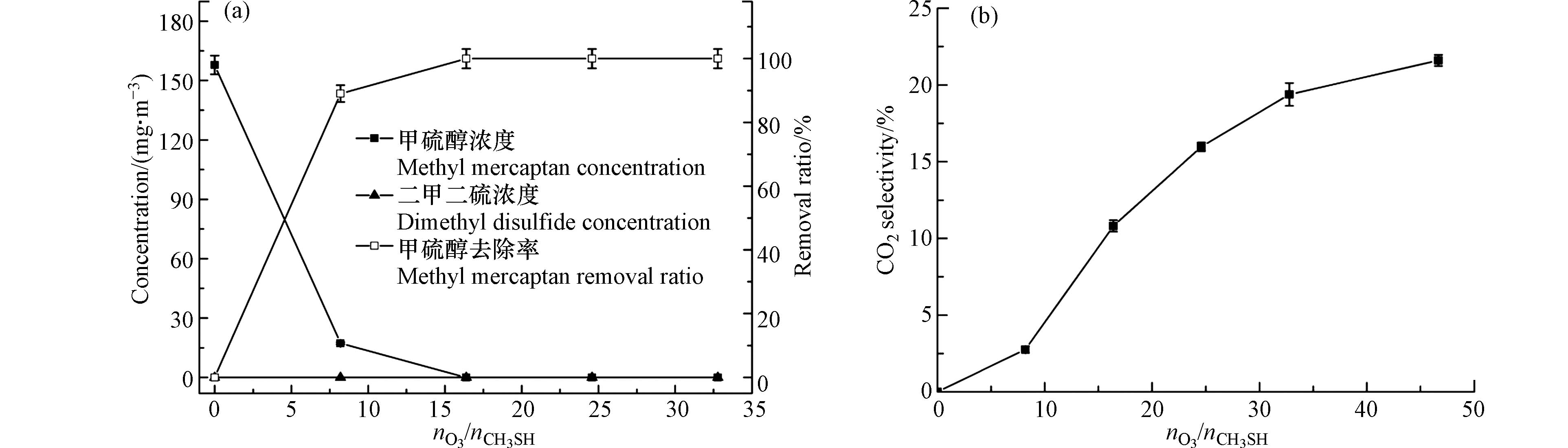
在臭氧对甲硫醇的氧化反应中,臭氧作为反应底物之一,其投加量对反应有较大的影响,且在实际应用中臭氧的投加量与能耗直接相关,因此,研究臭氧投加量的影响对于评价臭氧氧化降解甲硫醇工艺的技术经济性具有重要意义. 实验在室温((30±2)℃)条件下考察了臭氧投加量对甲硫醇去除率和二氧化碳选择性的影响,结果见图3. 由图3可知,对于初始浓度为157.9 mg·m−3的甲硫醇气体,反应时间为1.5 min时,甲硫醇去除率随臭氧投加量的增加而增大,当臭氧与甲硫醇的摩尔比为8.2时,甲硫醇的去除率达到91.3%;增加臭氧与甲硫醇的摩尔比至16.4,甲硫醇实现完全去除;臭氧对甲硫醇的氧化反应中二氧化碳选择性随臭氧投加量的增加呈现先快再缓的趋势,但整体看来其二氧化碳选择性较差,当臭氧与甲硫醇的摩尔比提高到46.7时,二氧化碳选择性仅为21.6%,这说明臭氧虽能将甲硫醇氧化去除,但将其完全矿化的难度较大. 通过对反应过程中二甲二硫浓度的监测发现,整个反应过程中二甲二硫被完全氧化,说明虽然氧气可将甲硫醇氧化为二甲二硫,但氧化性更强的臭氧对二甲二硫表现出更强的选择性,能够快速将二甲二硫氧化去除.
2.3 反应时间的影响
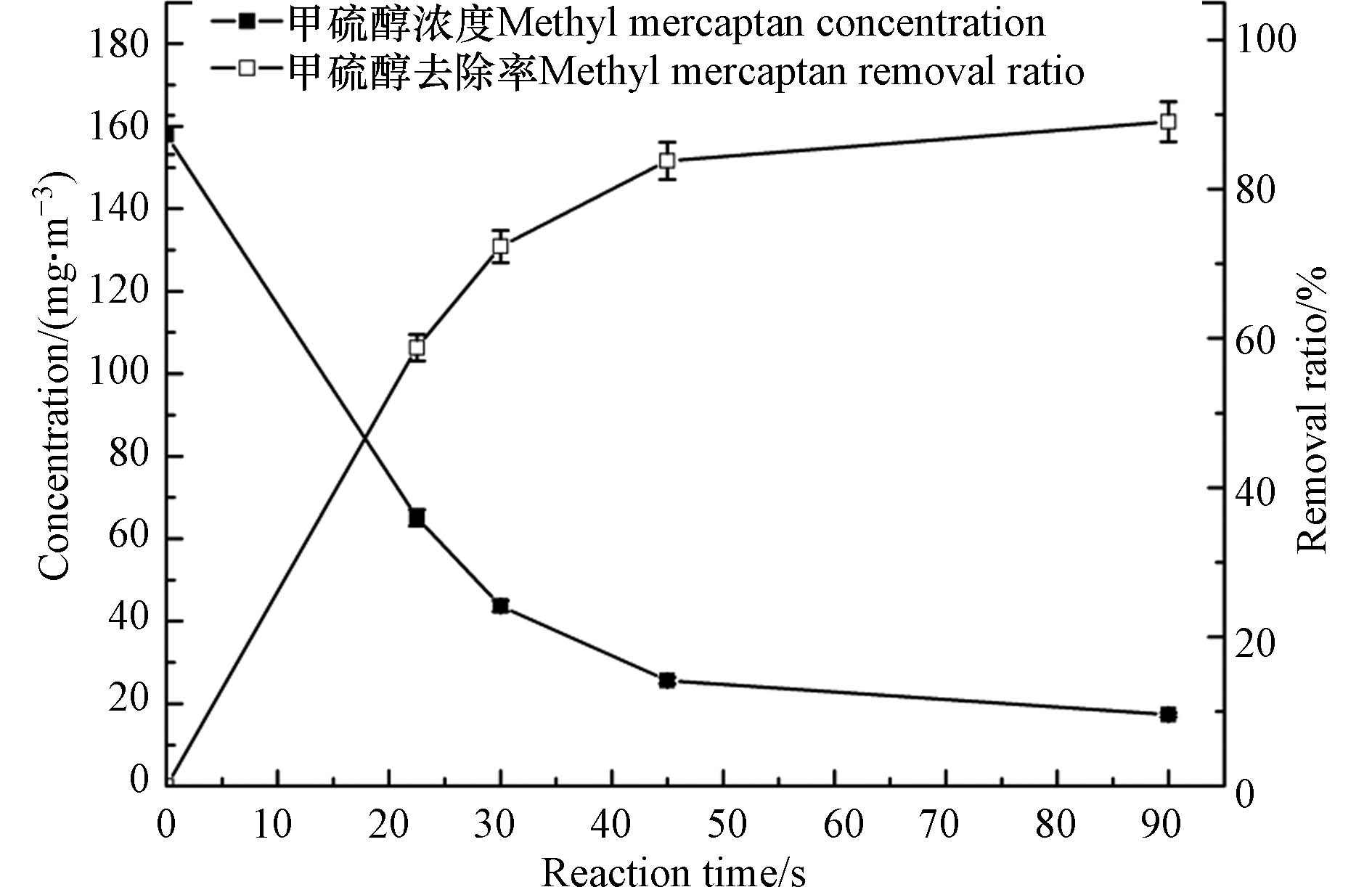
在臭氧对甲硫醇的氧化反应中,虽然臭氧具有强氧化性且其对甲硫醇的氧化反应属于均相反应,但反应时间对氧化性能的影响依然较大,研究反应时间的影响对于实际应用中接触反应器的设计具有重要意义. 实验通过调节反应气体流量研究了反应时间对臭氧氧化甲硫醇的影响,实验中甲硫醇初始浓度设定为157.9 mg·m−3,结果见图4. 由图4可以看出,甲硫醇的去除率随反应时间的延长而增大,当反应时间增加到45 s时,去除率达到81.8%,而将反应时间继续延长至90 s时,甲硫醇的去除率仅增加9.5%. 这主要是由于随着反应的进行气体中甲硫醇浓度降低,即反应底物浓度降低,反应速率降低.
为了更好地研究臭氧对甲硫醇的氧化降解动力学性能,参考文献[30]和[31]中臭氧氧化降解有机物的动力学特征进行研究. 由于臭氧投加量高于臭氧氧化甲硫醇的化学计量比,反应过程中臭氧浓度变化较小,分别采用伪一级反应动力学方程(式3)和伪二级反应动力学方程(式4)对臭氧氧化降解甲硫醇的动力学过程进行拟合,伪一级反应动力学模型拟合得到k1和R2分别为0.03995 s−1和0.9857,伪二级反应动力学模型拟合得到k2和R2分别为0.0005901 m3·mg−1·s−1和0.9639,可以看出两种动力学模型的拟合相关系数均较高. 分别采用式(5)和(6)所示的伪一级反应和伪二级反应半衰期计算公式对氧化动力学过程进行计算分析,计算得到伪一级反应和伪二级反应半衰期分别为17.35 s和10.74 s,而实验数据显示反应时间22.5 s时,甲硫醇的去除率58.77%,显然,17.35 s更接近实际数据. 因此,臭氧对气体中甲硫醇的氧化降解过程符合伪一级反应动力学模型.
y=1−e−k1t (3) (C0−Ct)/Ct=k2C0t (4) t1/2=ln2k1 (5) t1/2=1k2C0 (6) 式中,y为甲硫醇的去除率;C0为气体中甲硫醇的初始浓度,mg·m−3;Ct为反应时刻t气体中甲硫醇的浓度,mg·m−3;k1为伪一级反应速率常数,s−1;k2为伪二级反应速率常数,m3·mg−1·s−1;t 为反应时间,s.
2.4 反应温度的影响
反应温度是臭氧氧化反应的一个重要参数,其直接影响反应效率和能耗. 因此,实验通过调节水浴温度来实现反应温度的调节,从而研究了反应温度对臭氧氧化甲硫醇性能的影响,实验中甲硫醇初始浓度设定为157.9 mg·m−3,结果见图5. 由图5可以看出,在反应温度低于50 ℃时,甲硫醇的去除率随反应温度升高而增大,而随着反应温度升高至50 ℃以上,臭氧对甲硫醇的氧化去除率不再随反应温度的变化而变化,结合能耗综合考虑,臭氧对甲硫醇的最佳反应温度宜为50 ℃. 但由于反应温度由20 ℃到50 ℃,甲硫醇的去除率仅增加不到13%,且实际应用过程中气体温度常在30 ℃左右,因此,结合能耗综合考虑实际应用时可不采取升温措施.
2.5 湿度的影响
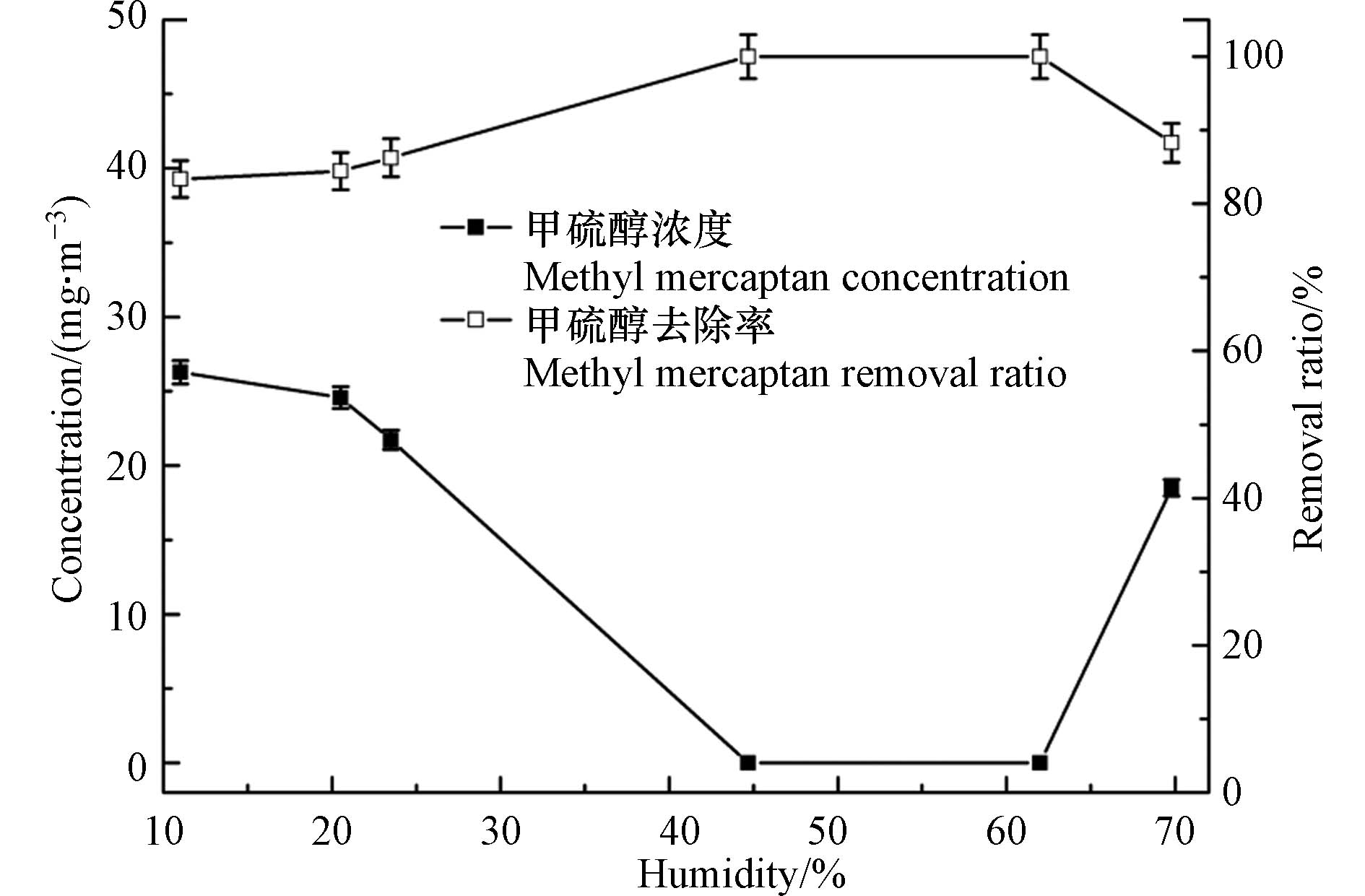
气体的湿度对甲硫醇的极化状态、臭氧的稳定性、反应产物的存在形态等均有较大的影响. 因此,实验通过超声雾化加湿装置对反应气体湿度进行了调节,从而研究了气体湿度对臭氧氧化甲硫醇性能的影响,实验中甲硫醇初始浓度设定为157.9 mg·m−3,结果见图6. 由图6可以看出,湿度对于臭氧氧化甲硫醇影响较大,过高和过低的湿度均不利于反应的进行,这主要是由于适当的湿度可促使臭氧生成氧化性更强的羟基自由基,进而实现甲硫醇去除率的提高[32];过高的湿度则会存在水汽的凝结形成雾滴,而雾滴会对气体的传质造成影响,且由于甲硫醇不溶于水,溶解于雾滴中的臭氧很难通过非均相反应氧化甲硫醇,致使有效臭氧浓度降低,从而影响臭氧对甲硫醇的去除率. 因此,在实际应用中应将气体湿度调节至45%—62%,以获得最佳的甲硫醇去除效果.
2.6 甲硫醇的氧化降解产物
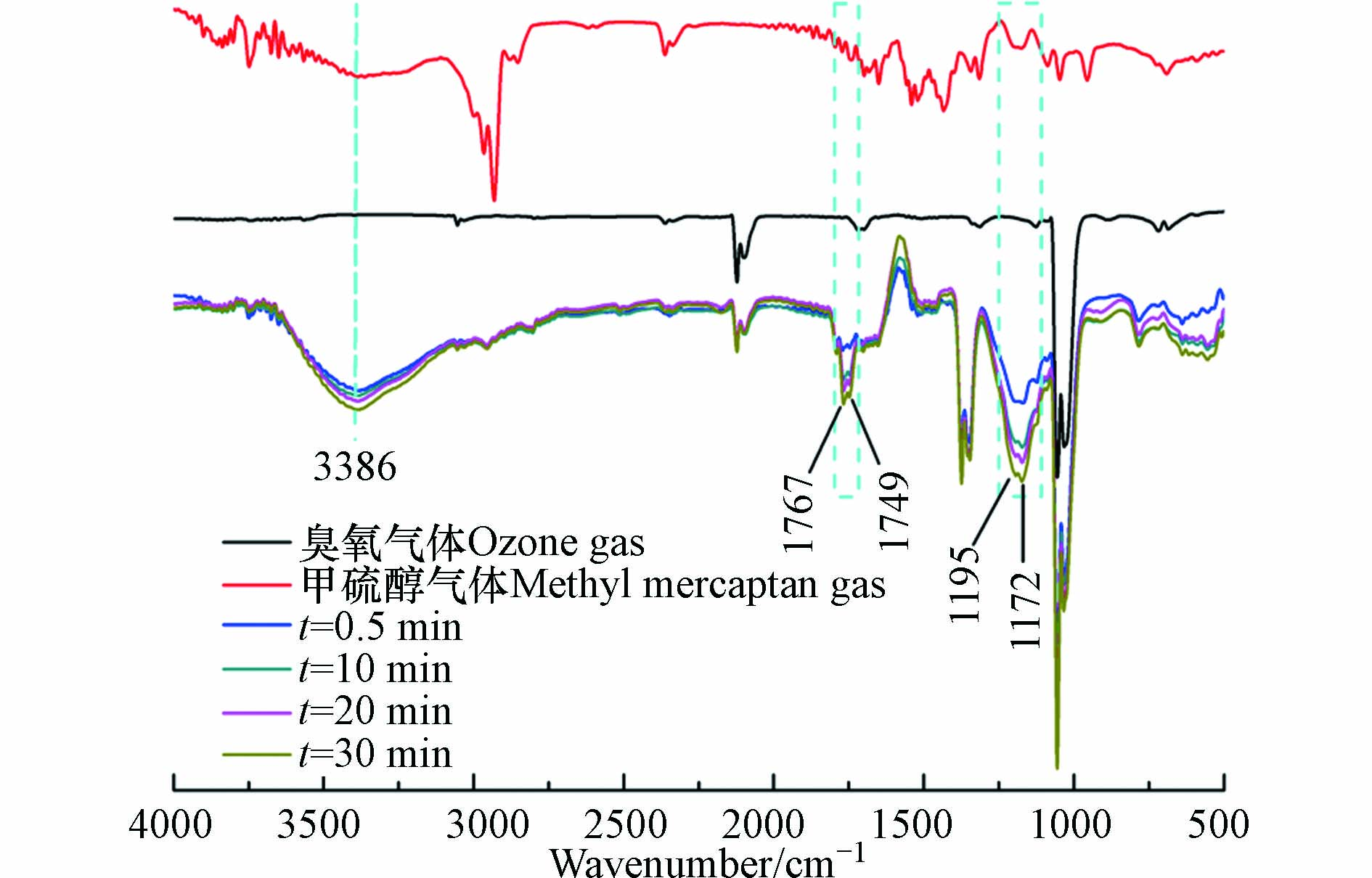
为了进一步研究臭氧对气体中甲硫醇的氧化降解过程,采用原位红外光谱和离子色谱技术对甲硫醇的氧化降解产物进行研究. 按照1.3节所述方法测得臭氧对气体中甲硫醇的氧化降解原位红外光谱如图7所示. 由图7可知,氧化过程中3386 cm−1处的O—H(H2O)伸缩振动吸收峰随反应时间的延长而增强,说明氧化过程伴随有水的生成;1767 cm−1和1749 cm−1处的醛和酮C=O伸缩振动吸收峰随反应的进行而增强,说明氧化过程中有醛和酮的生成;1172 cm−1和1195 cm−1是臭氧吸收峰的一部分,随着氧化反应的进行,该吸收峰逐渐增强,这主要是由于反应生成的化合物中C—H振动吸收峰与臭氧吸收峰叠加引起的[33].
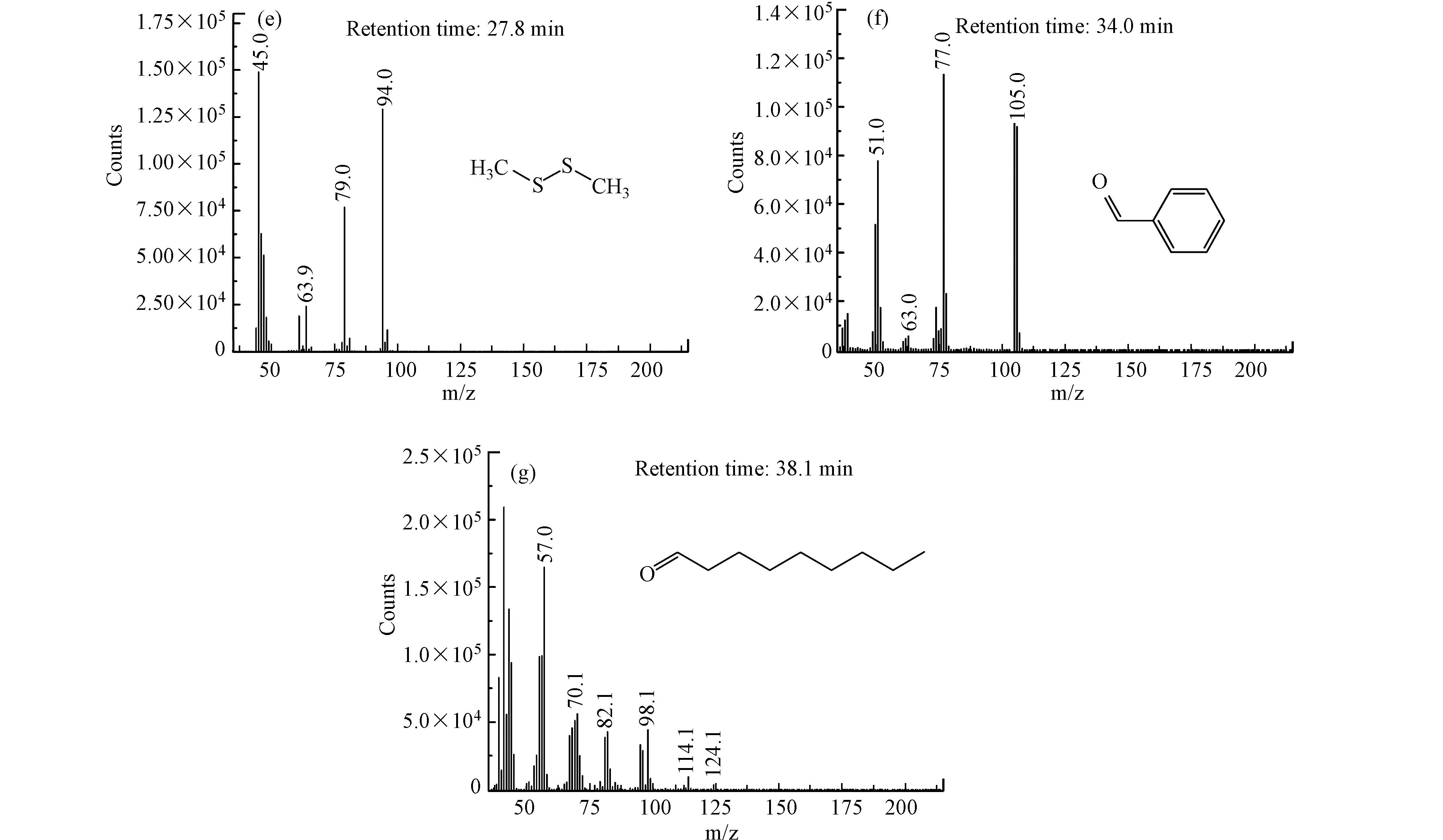
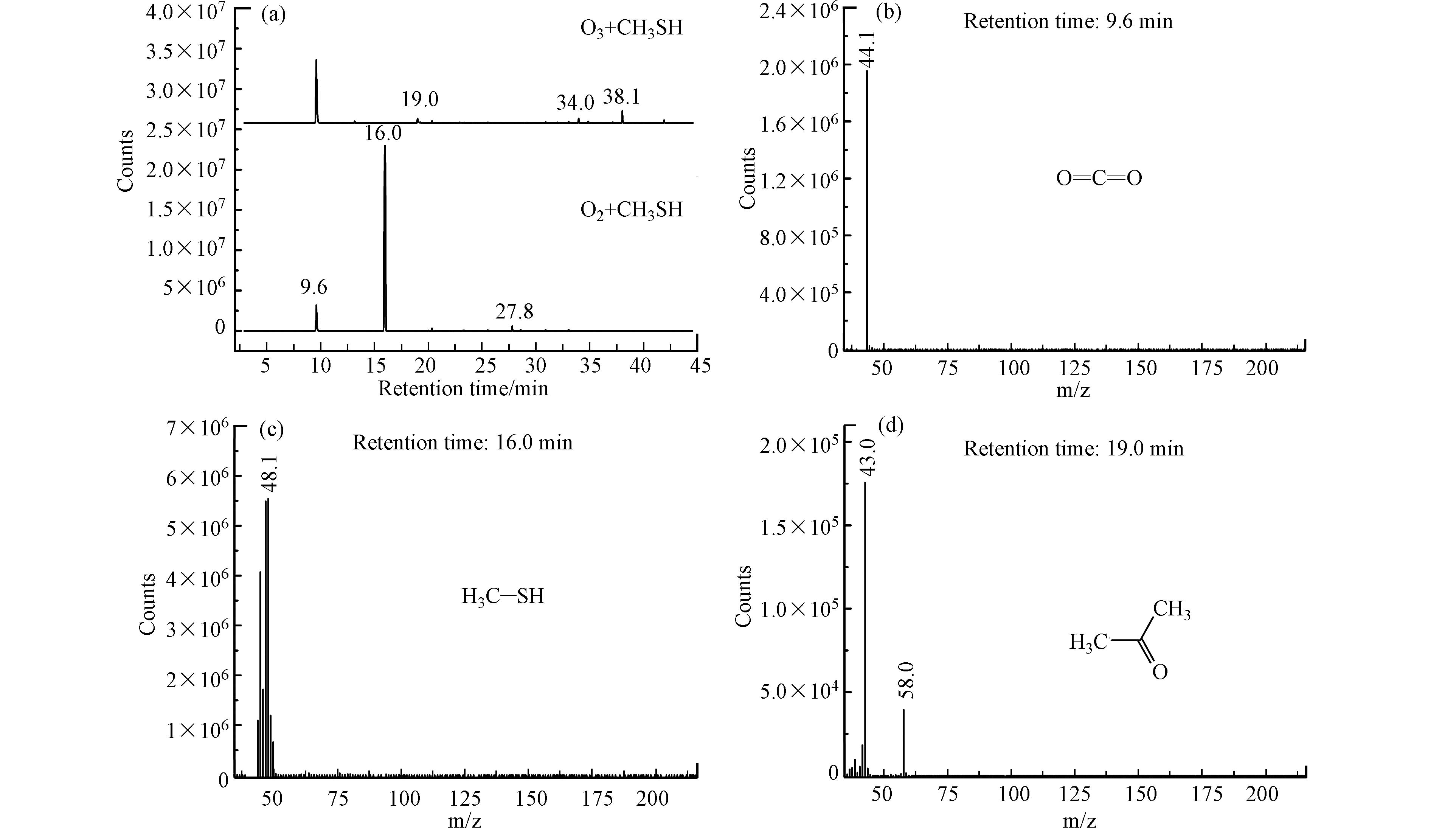
按照1.3节所述测试方法对反应后气体中甲烷含量进行分析,结果表明,反应后气体中无甲烷生成. 采用气袋采样-预浓缩/气相色谱-质谱法(GC-MS)对氧气甲硫醇混合气和臭氧甲硫醇混合气进行分析,结果如图8所示.
图8中(a)为GC-MS总离子流色谱图,图8(b)—(g)为不同保留时间出峰物质的质谱图. 由图8可以看出,由于采用制氧机所制氧气为氧源,气体中含有一定量的二氧化碳;在氧气存在下,甲硫醇被部分氧化为二甲二硫,该现象在2.1节已被证实;臭氧引入后,气体中二氧化碳浓度升高,说明臭氧可将部分甲硫醇矿化为二氧化碳,该现象与2.2节结果保持一致;臭氧净化气体中未检测到含硫有机化合物,说明甲硫醇被氧化降解为无机硫化物或单质硫;净化气体中检测到少量丙酮、苯甲醛和壬醛等醛酮类物质,且GC-FID未检测到甲烷的生成,说明甲硫醇的初步氧化降解产物可能为小分子烯烃(由于其分子量较小,GC-MS无法检测),小分子烯烃一部分被氧化降解为二氧化碳,少量烯烃在臭氧、自由基等作用下引发加成反应,并在水存在下生成少量醛酮化合物,这与红外光谱表征结果相一致.
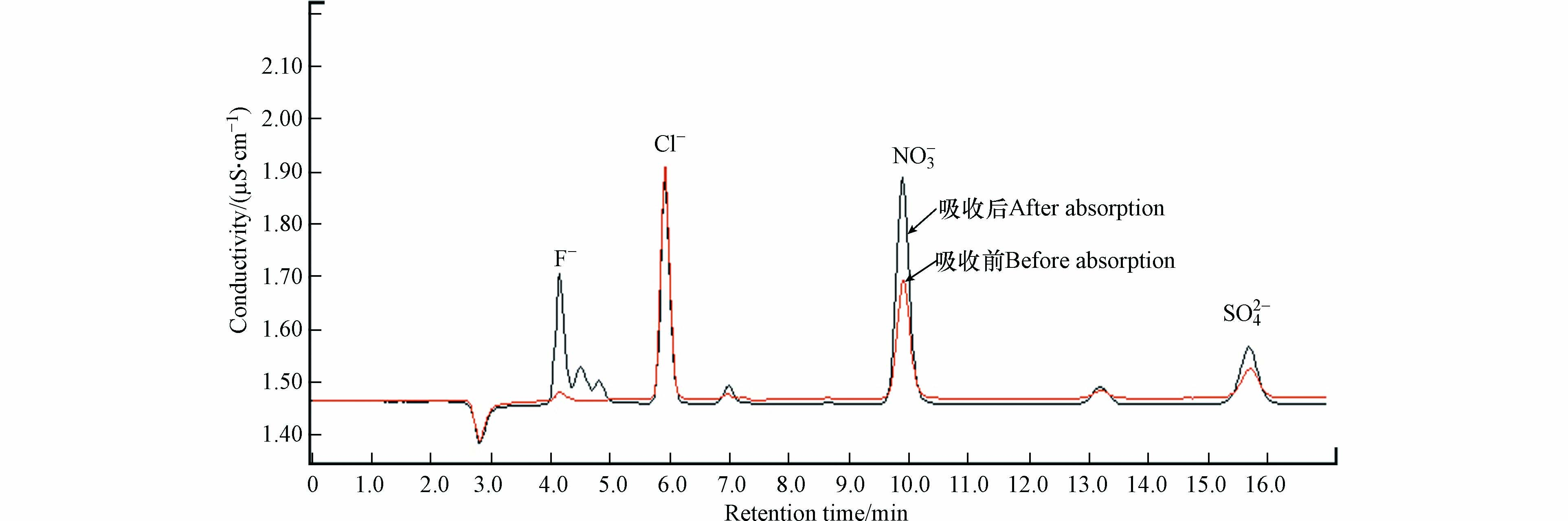
为了获得甲硫醇中硫的去向,按照1.3节所述测试方法对臭氧氧化降解甲硫醇过程中可能生成的硫氧化物进行测定,测试过程中臭氧氧化甲硫醇的反应条件为:甲硫醇初始浓度为157.9 mg·m−3,臭氧与甲硫醇摩尔比为32.8,反应时间为90 s,反应温度为30 ℃,湿度为46.5%. 吸收前后吸收液的离子色谱分析结果见图9和表1.
表 1 吸收前后吸收液中阴离子浓度Table 1. Anion concentration in absorption solution before and after absorption吸收液 Absorption solution F− /(mg·L−1) Cl−/(mg·L−1) NO3− /(mg·L−1) SO42− /(mg·L−1) 吸收前 0.42 3.55 4.96 1.62 吸收后 1.29 3.49 8.54 2.69 结果表明,吸收后吸收液中F−、NO3−浓度升高,其中NO3−浓度的升高主要是由于制氧机制备得到的氧气中含有少量氮气,当其进入臭氧发生器时经电晕放电生成二氧化氮,进而被吸收液吸收后生成NO3−;F−浓度升高主要是由于臭氧发生器及各种管路中均采用了大量的含氟制品引起的. 吸收后吸收液中SO42-浓度也有所升高,且未检测到SO32-等其他含硫阴离子,这说明甲硫醇被臭氧氧化生成的硫氧化物均为三氧化硫. 利用测得数据换算得到气体中三氧化硫的浓度为4.4 mg·m−3,其硫含量仅占甲硫醇气体中硫含量的1.69%,证明硫氧化物不是甲硫醇中硫的主要去向,且采用GC-FPD也未检测到H2S和含硫有机物的生成. 因此,推测甲硫醇中硫的主要氧化产物为硫单质,这与文献[34]中甲硫醇的催化氧化产物为甲磺酸的报道是不一致的,这也说明以氧气为氧化剂的催化氧化和O3对甲硫醇的直接氧化机理是不一致的.
3. 结论(Conclusion)
(1)氧气可将甲硫醇氧化为二甲二硫,但远低于臭氧对甲硫醇的氧化去除性能.
(2)甲硫醇去除率随臭氧投加量的增加而增大,当臭氧与甲硫醇的摩尔比为8.2时,甲硫醇的去除率达到91.3%,增加臭氧与甲硫醇的摩尔比至16.4,甲硫醇可实现完全去除.
(3)甲硫醇的去除率随反应时间的延长而增大,臭氧对气体中甲硫醇的氧化降解过程符合伪一级动力学反应模型,其反应速率常数为0.03995 s−1,甲硫醇的半衰期为17.35 s.
(4)甲硫醇的去除率随反应温度升高而增大,而随着反应温度升高至50 ℃以上,臭氧对甲硫醇的氧化去除率不再随反应温度的变化而变化,结合能耗综合考虑,其最佳反应温度宜为50 ℃.
(5)过高和过低的湿度均不利于反应的进行,其最佳反应相对湿度为45%—62%.
(6)臭氧氧化降解甲硫醇的最佳反应条件为:臭氧与甲硫醇摩尔比16.4,反应时间45 s,反应温度50 ℃,反应相对湿度45%—62%.
(7)采用原位红外光谱、气相色谱-质谱联用和离子色谱技术对臭氧氧化降解甲硫醇过程的研究证明,考察条件下,臭氧不能将全部甲硫醇矿化为二氧化碳和水,而是生成了部分醛类和酮类中间产物,且甲硫醇中硫的主要氧化产物为硫单质.
(8)综合考虑臭氧氧化甲硫醇的最佳反应条件和降解产物,该工艺存在能耗高、易造成二次污染等不足,在实际应用中不建议采用臭氧直接氧化工艺对含甲硫醇臭气进行净化.
-
表 1 过渡态理论(TST)结合隧道效应校正 (κ)和不同单点能方法计算的模型化合物的kOH (cm3·molecule−1·s−1)
Table 1. kOH (cm3·molecule−1·s−1) of selected compounds calculated by the combination transition-state theory (TST) with different transmission coefficient (κ) correction and single-point-energy calculation methods.
单点能方法Zero-point energy method κ 化合物Compound CF3CF2H CF3CH2CF3 CF3CF2(CHF)2CF3 CF2=CH2 CF3(CF2)7CH=CH2 实测值 6.25 × 10−15 9.57 × 10−16 3.29 × 10−15 2.49 × 10−12 1.36 × 10−12 M06-2X-D3/aug-cc-pVTZ κS 4.11 × 10−15 1.16 × 10−15 8.55 × 10−15 1.58 × 10−12 1.34 × 10−13 κW 1.27 × 10−15 1.79 × 10−16 3.98 × 10−15 1.55 × 10−12 1.84 × 10−13 M06-2X-D3/may-cc-pVTZ κS 3.19 × 10−15 9.33 × 10−16 6.86 × 10−15 8.18 × 10−13 1.22 × 10−13 κW 9.22 × 10−16 1.35 × 10−16 2.96 × 10−15 1.02 × 10−12 1.48 × 10−13 M06-2X-D3/jun-cc-pVTZ κS 3.50 × 10−15 1.01 × 10−15 7.28 × 10−15 1.23× 10−12 1.24 × 10−13 κW 1.03 × 10−15 1.49 × 10−16 3.20 × 10−15 1.20 × 10−12 1.55 × 10−13 M06-2X-D3/jul-cc-pVTZ κS 3.78 × 10−15 1.10 × 10−15 8.05 × 10−15 1.51 × 10−12 1.31 × 10−13 κW 1.14 × 10−15 1.67 × 10−16 3.67 × 10−15 1.48 × 10−12 1.73 × 10−13 M06-2X-D3/def2-TZVP κS 2.96 × 10−15 9.03 × 10−16 6.51 × 10−15 8.07× 10−13 1.33 × 10−13 κW 8.40 × 10−16 1.29 × 10−16 2.75 × 10−15 9.62 × 10−13 1.88 × 10−13 M06-2X-D3/def2-TZVPP κS 4.27 × 10−15 1.12 × 10−15 8.28 × 10−15 7.25 × 10−13 1.14 × 10−13 κW 1.33 × 10−15 1.71 × 10−16 3.80 × 10−15 8.58 × 10−13 1.34 × 10−13 M06-2X-D3/pcseg-2 κS 2.50 × 10−15 6.47 × 10−16 5.31 × 10−15 4.81 × 10−13 7.27 × 10−14 κW 6.79 × 10−16 8.47 × 10−17 2.10 × 10−15 5.57 × 10−13 7.52 × 10−14 M06-2X-D3/MG3S κS 4.16 × 10−15 1.18 × 10−15 1.18 × 10−14 1.59 × 10−12 1.32 × 10−13 κW 1.29 × 10−15 1.82 × 10−16 6.08 × 10−15 1.56 × 10−12 1.71 × 10−13 ωB97X-D/aug-cc-pVTZ κS 3.99 × 10−14 4.43 × 10−15 3.45 × 10−14 5.10 × 10−11 4.72 × 10−12 κW 2.72 × 10−14 1.08 × 10−15 2.96 × 10−14 4.99 × 10−11 4.54 × 10−12 ωB97X-D/may-cc-pVTZ κS 3.34 × 10−14 3.65 × 10−15 2.92 × 10−14 3.51 × 10−11 3.84 × 10−12 κW 2.08 × 10−14 8.32 × 10−16 2.26 × 10−14 3.44 × 10−11 3.69 × 10−12 ωB97X-D/jun-cc-pVTZ κS 3.57 × 10−14 3.97 × 10−15 3.09 × 10−14 4.17 × 10−11 4.10 × 10−12 κW 2.30 × 10−14 9.34 × 10−16 2.48 × 10−14 4.11 × 10−11 3.94 × 10−12 ωB97X-D/jul-cc-pVTZ κS 3.75 × 10−14 4.24 × 10−15 3.31 × 10−14 4.88 × 10−11 4.51 × 10−12 κW 2.47 × 10−14 1.02 × 10−15 2.77× 10−14 4.78 × 10−11 4.34 × 10−12 ωB97X-D/def2-TZVP κS 3.43 × 10−14 4.49 × 10−15 3.27 × 10−14 2.94 × 10−11 5.78 × 10−12 κW 2.17 × 10−14 1.09 × 10−15 2.71 × 10−14 2.88 × 10−11 5.56 × 10−12 ωB97X-D/def2-TZVPP κS 4.29 × 10−14 5.29 × 10−15 3.70 × 10−14 2.99 × 10−11 4.56 × 10−12 κW 3.07 × 10−14 1.36 × 10−15 3.33 × 10−14 2.93 × 10−11 4.38 × 10−12 ωB97X-D/pcseg-2 κS 2.53 × 10−14 2.93 × 10−15 2.35 × 10−14 2.06 × 10−11 2.58 × 10−12 κW 1.40 × 10−14 6.24 × 10−16 1.63 × 10−14 2.01 × 10−11 2.53 × 10−12 ωB97X-D/MG3S κS 4.93× 10−14 5.99 × 10−15 5.07 × 10−14 8.90 × 10−11 1.08 × 10−11 κW 3.75 × 10−14 1.59 × 10−15 5.65 × 10−14 8.71 × 10−11 1.04 × 10−11 表 2 理论计算lgkOH的平均绝对误差(MAE) (kOH: cm3·molecule−1·s−1)
Table 2. Mean absolute deviation (MAE) values of theoretical lgkOH for selected compounds. (kOH: cm3·molecule−1·s−1)
单点能方法 Zero-point energy method MAE (TST × κW) MAE (TST × κS) HFCs和HFCs HFCs HFOs HFCs和HFCs HFCs HFOs M06-2X-D3/aug-cc-pVTZ 0.47 0.45 0.50 0.34 0.20 0.56 M06-2X-D3/may-cc-pVTZ 0.57 0.53 0.64 0.39 0.17 0.72 M06-2X-D3/jun-cc-pVTZ 0.53 0.49 0.59 0.36 0.18 0.63 M06-2X-D3/jul-cc-pVTZ 0.49 0.46 0.52 0.35 0.19 0.58 M06-2X-D3/def2-TZVP 0.58 0.56 0.60 0.38 0.17 0.69 M06-2X-D3/def2-TZVPP 0.54 0.44 0.69 0.41 0.18 0.75 M06-2X-D3/pcseg-2 0.78 0.69 0.91 0.50 0.21 0.93 M06-2X-D3/MG3S 0.51 0.51 0.51 0.37 0.24 0.56 ωB97x-D/aug-cc-pVTZ 0.74 0.59 0.95 0.91 0.87 0.97 ωB97X-D/may-cc-pVTZ 0.63 0.50 0.83 0.81 0.80 0.84 ωB97X-D/jun-cc-pVTZ 0.66 0.52 0.88 0.85 0.83 0.89 ωB97X-D/jul-cc-pVTZ 0.71 0.56 0.93 0.89 0.85 0.95 ωB97X-D/def2-TZVP 0.68 0.55 0.88 0.86 0.85 0.89 ωB97X-D/def2-TZVPP 0.73 0.66 0.83 0.89 0.92 0.84 ωB97X-D/pcseg-2 0.51 0.43 0.63 0.67 0.69 0.64 ωB97X-D/MG3S 0.97 0.79 1.25 1.11 1.00 1.27 表 3 模型化合物与·OH反应的能垒(ΔE: kJ·mol−1, 0 K)、标准活化自由能(ΔG‡,0: kJ·mol−1, 298 K)、反应焓变(ΔrH: kJ·mol−1, 298 K)、过渡态虚频(υi†: cm−1)和kOH (cm3·molecule−1 s−1, 298 K)的计算值
Table 3. Calculated energy barrier (ΔE: kJ·mol−1, 0 K), the standard Gibbs free energy of activation (ΔG‡,0: kJ·mol−1, 298 K), enthalpy (ΔH: kJ·mol−1, 298 K), frequency of TSs (υi†: cm−1) and kOH (cm3·molecule−1·s−1, 298 K) values for selected compounds reacting with ·OH.
反应通道 Reaction pathway κ 单点能方法 Zero-point energy method ΔG‡,0 ∆E ΔH υi† kOH CF3CH2F 实测kOH:6.25 × 10−15 计算kOH:2.96 × 10−15 1a, 2a κS M06-2X-D3/def2-TZVP 52.90 17.71 −62.67 1461.49 1.48 × 10−15 CF3CH2CF3 实测kOH:9.57 × 10−16 计算kOH:9.03× 10−16 1b κS M06-2X-D3/def2-TZVP 58.07 23.16 −46.48 1575.73 4.00 × 10−16 2b κS M06-2X-D3/def2-TZVP 57.61 22.83 −43.77 1600.20 5.03 × 10−16 CF3CF2(CHF)2CF3 实测kOH:3.29 × 10−15 计算kOH:6.51 × 10−15 1c κS M06-2X-D3/def2-TZVP 52.08 15.42 −73.12 1486.68 1.79 × 10−15 2c M06-2X-D3/def2-TZVP 48.77 12.75 −74.71 1429.22 4.73 × 10−15 CF2=CH2 实测kOH:2.49 × 10−12 计算kOH:1.55 × 10−12 1d, 2d κW M06-2X-D3/aug-cc-pVTZ 67.08 8.22 −3.11 1344.44 1.23 × 10−18 3d, 4d κW M06-2X-D3/aug-cc-pVTZ 33.54 −0.15 −128.79 437.72 4.00 × 10−13 5d, 6d κW M06-2X-D3/aug-cc-pVTZ 33.62 −0.64 −186.12 392.38 3.76 × 10−13 CF3(CF2)7CH=CH2 实测kOH:1.36 × 10−12 计算kOH:1.84 × 10−13 1e κW M06-2X-D3/aug-cc-pVTZ 59.06 25.11 −25.63 1532.35 3.73 × 10−17 2e κW M06-2X-D3/aug-cc-pVTZ 61.97 25.33 −24.34 1619.52 1.25 × 10−17 3e κW M06-2X-D3/aug-cc-pVTZ 60.40 25.27 −23.02 1527.16 2.16 × 10−17 4e κW M06-2X-D3/aug-cc-pVTZ 43.50 6.34 −129.20 536.44 7.76 × 10−15 5e κW M06-2X-D3/aug-cc-pVTZ 35.72 0.64 −127.38 497.65 1.74 × 10−13 6e κW M06-2X-D3/aug-cc-pVTZ 46.68 8.99 −118.41 470.14 2.04 × 10−15 -
[1] HODNEBROG, ETMINAN M, FUGLESTVEDT J S, et al. Global warming potentials and radiative efficiencies of halocarbons and related compounds: A comprehensive review [J]. Reviews of Geophysics, 2013, 51(2): 300-378. doi: 10.1002/rog.20013 [2] ABAS N, KALAIR A R, KHAN N, et al. Natural and synthetic refrigerants, global warming: A review [J]. Renewable and Sustainable Energy Reviews, 2018, 90: 557-569. doi: 10.1016/j.rser.2018.03.099 [3] BIRMPILI T. Montreal protocol at 30: The governance structure, the evolution, and the Kigali amendment [J]. Comptes Rendus Geoscience, 2018, 350(7): 425-431. doi: 10.1016/j.crte.2018.09.002 [4] FLERLAGE H, VELDERS G J M, de BOER J. A review of bottom-up and top-down emission estimates of hydrofluorocarbons (HFCs) in different parts of the world [J]. Chemosphere, 2021, 283: 131208. doi: 10.1016/j.chemosphere.2021.131208 [5] YI L Y, WU J, AN M D, et al. The atmospheric concentrations and emissions of major halocarbons in China during 2009-2019 [J]. Environmental Pollution, 2021, 284: 117190. doi: 10.1016/j.envpol.2021.117190 [6] GLIGOROVSKI S, STREKOWSKI R, BARBATI S, et al. Environmental implications of hydroxyl radicals ((•)OH) [J]. Chemical Reviews, 2015, 115(24): 13051-13092. doi: 10.1021/cr500310b [7] SUN X Y, HU Y M, XU F, et al. Mechanism and kinetic studies for OH radical-initiated atmospheric oxidation of methyl propionate [J]. Atmospheric Environment, 2012, 63: 14-21. doi: 10.1016/j.atmosenv.2012.08.045 [8] LIAO Z H, ZENG M, WANG L M. Atmospheric oxidation mechansim of polychlorinated biphenyls (PCBs) initiated by OH radicals [J]. Chemosphere, 2020, 240: 124756. doi: 10.1016/j.chemosphere.2019.124756 [9] SHI X L, ZHANG R M, LI Y F, et al. Mechanism theoretical study on OH-initiated atmospheric oxidation degradation of dimethoate [J]. Journal of Molecular Structure, 2018, 1163: 61-67. doi: 10.1016/j.molstruc.2018.02.104 [10] HOLTOMO O, NGUE'ZEO H, NSANGOU M, et al. Theoretical investigation of the atmospheric implication for the reaction of •OH radical with CF2C(CH3)-CX3, X = H, F [J]. Journal of Molecular Graphics and Modelling, 2021, 106: 107905. doi: 10.1016/j.jmgm.2021.107905 [11] GUPTA P, RAJAKUMAR B. A theoretical insight on the kinetics for the reaction of (E)-/ (Z)-CHF=CF(CF2)x=1, 2CF3 with OH radicals under tropospheric conditions [J]. Journal of Fluorine Chemistry, 2019, 222/223: 31-45. doi: 10.1016/j.jfluchem.2019.04.009 [12] JABEEN F, KUMAR A, RAJAKUMAR B. Kinetics, thermochemistry and atmospheric implications for the reaction of OH radicals with CH3CF = CF2 (HFO-1243yc) [J]. Chemical Physics Letters, 2020, 758: 137933. doi: 10.1016/j.cplett.2020.137933 [13] GOGOI P, PAUL S, MISHRA B K, et al. Tropospheric oxidation of 1H-heptafluorocyclopentene (cyc-CF2CF2CF2CF═CH–) with OH radicals: Reaction mechanism, kinetics, and global warming potentials [J]. ACS Earth and Space Chemistry, 2021, 5(7): 1792-1800. doi: 10.1021/acsearthspacechem.1c00124 [14] XU C, WANG C Y, LI B, et al. Theoretical study on the reaction mechanism of OH radical with Z(E)-CF3CH CHF [J]. Physical Chemistry Chemical Physics, 2019, 21(3): 1367-1374. doi: 10.1039/C8CP06647G [15] HSU K J, DEMORE W B. Rate constants and temperature dependences for the reactions of hydroxyl radical with several halogenated methanes, ethanes, and propanes by relative rate measurements [J]. The Journal of Physical Chemistry, 1995, 99(4): 1235-1244. doi: 10.1021/j100004a025 [16] CHEN L, UCHIMARU T, KUTSUNA S, et al. Kinetics study of gas-phase reactions of erythro/threo-CF3CHFCHFC2F5 with OH radicals at 253-328 K [J]. Chemical Physics Letters, 2010, 488(1/2/3): 22-26. [17] TOKUHASHI K, TAKIZAWA K, KONDO S. Rate constants for the reactions of OH radicals with fluorinated ethenes: Kinetic measurements and correlation between structure and reactivity [J]. The Journal of Physical Chemistry. A, 2018, 122(19): 4593-4600. doi: 10.1021/acs.jpca.7b11653 [18] ANDERSEN M P S, NIELSEN O J, TOFT A, et al. Atmospheric chemistry of CxF2x + 1CHCH2 (x = 1, 2, 4, 6, and 8): Kinetics of gas-phase reactions with Cl atoms, OH radicals, and O3 [J]. Journal of Photochemistry and Photobiology A:Chemistry, 2005, 176(1/2/3): 124-128. [19] SUTCLIFFE B T, WOOLLEY R G. On the quantum theory of molecules [J]. The Journal of Chemical Physics, 2012, 137(22): 22A-544A. [20] KÜHNE T D, IANNUZZI M, del BEN M, et al. CP2K: An electronic structure and molecular dynamics software package - Quickstep: Efficient and accurate electronic structure calculations [J]. The Journal of Chemical Physics, 2020, 152(19): 194103. doi: 10.1063/5.0007045 [21] ZHAO Y, TRUHLAR D G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals [J]. Theoretical Chemistry Accounts, 2008, 120(1): 215-241. [22] DUNNING T H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen [J]. The Journal of Chemical Physics, 1989, 90(2): 1007-1023. doi: 10.1063/1.456153 [23] FRISCH M, TRUCKS G, SCHLEGEL H, et al. Gaussian 09, rev[CP]. Gaussian Inc, Wallingford, 2009 [24] LI C, XIE H B, CHEN J W, et al. Predicting gaseous reaction rates of short chain chlorinated paraffins with ·OH: Overcoming the difficulty in experimental determination [J]. Environmental Science & Technology, 2014, 48(23): 13808-13816. [25] CHAI J D, HEAD-GORDON M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections [J]. Physical Chemistry Chemical Physics, 2008, 10(44): 6615-6620. doi: 10.1039/b810189b [26] WEIGEND F. Accurate Coulomb-fitting basis sets for H to Rn [J]. Physical Chemistry Chemical Physics, 2006, 8(9): 1057-1065. doi: 10.1039/b515623h [27] FERNANDEZ-RAMOS A, ELLINGSON B A, GARRETT B C, et al. Variational transition state theory with multidimensional tunneling[M]//Reviews in Computational Chemistry. Hoboken, NJ, USA: John Wiley & Sons, Inc. , 2007: 125-232. [28] WIGNER E. The transition state method [J]. Transactions of the Faraday Society, 1938, 34: 29-41. doi: 10.1039/tf9383400029 [29] DOUBLEDAY C, ARMAS R, WALKER D, et al. Heavy-atom tunneling calculations in thirteen organic reactions: Tunneling contributions are substantial, and Bell's formula closely approximates multidimensional tunneling at ≥250 K [J]. Angewandte Chemie (International Ed. in English), 2017, 56(42): 13099-13102. doi: 10.1002/anie.201708489 [30] SKODJE R T, TRUHLAR D G. Parabolic tunneling calculations [J]. The Journal of Physical Chemistry, 1981, 85(6): 624-628. doi: 10.1021/j150606a003 期刊类型引用(0)
其他类型引用(1)
-






 下载:
下载: