1）Archie公式。Archie 在1942年首次建立了适用于饱和砂土的电阻率模型，该模型体现出了电阻率与孔隙水电阻率及孔隙率之间的相关关系，其关系式如式(1)所示^[19]。

式中：$\rho$为实测土体电阻率，Ω·m；${\rho _{\text{w}}}$为孔隙水电阻率，Ω·m；n为孔隙率；a为土性参数；m为胶结系数。

最早的Archie公式由于仅适用于饱和的无黏性土中，存在一定的局限性。对此，有许多学者在原有的基础上进行了修正和改进，比如KELLER等^[20]在Archie的基础上，重新提出了适用于非饱和无黏性砂土的电阻率结构模型，其关系式如式(2)所示。

式中：S_r为饱和度；P为饱和度指数。

而对于黏性土，WAXMAN^[21]在此基础上，建立了非饱和黏性土的电阻率模型，其关系式如式(3)所示。

式中：$B$为双电层中与土颗粒表面电性相反电荷的电导率；$Q$为单位土体孔隙中阳离子交换容量；$S$为黏土的比表面积；$BQ$为土体颗粒表面双电层的电导率。

国内学者储亚等^[22]也基于Archie公式建立了非饱和黏性土的电阻率模型，关系式如式(4)所示。

式中：${P_r}$为体积含水率，%；d为体积含水率系数；$N$为污染物掺量，mg·kg⁻¹；$f$为污染物掺量系数，$D$为拟合参数。

从WAXMAN和储亚这2位学者针对于黏性土建立的电阻率模型来看，2种模型表达式的结构是一致的，而且第2 种模型中体积含水率也仅是与孔隙率和饱和度有关。

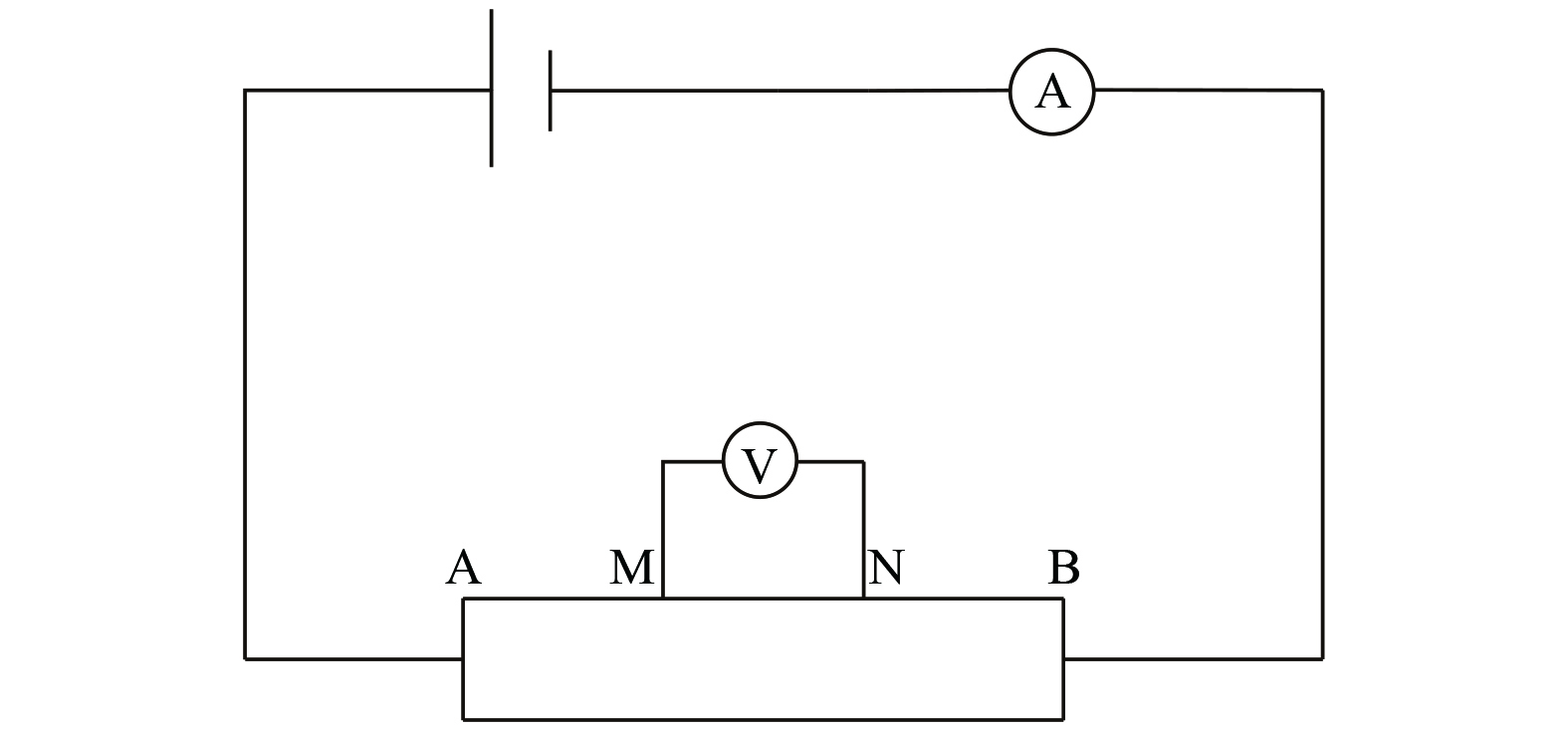
2）室内电阻率测试原理。在室内电阻率测量中，主要采用对称四极法，常用的四极测试装置主要由供电电极A、B和测量电极M、N组成，如图1所示。分别测得其试样的电压Ｕ及电流值Ｉ后，即可通过欧姆定律改写公式求得试样的电阻率ρ^[23]，即如式(5)所示。

式中：S为试样横截面面积，m²；L为电极M、N之间的距离，m。

本次试验所用红黏土取自贵州大学物探试验场地，取土深度为1~3 m。按照《土工试验方法标准》（GB/T 50123—2019）测取该土样的基本物性参数，其结果见表1所示。

将取回的红黏土烘干、磨碎，过2.0 mm的筛进行颗粒级配筛分后，将土样再烘干冷却后密封保存备用。在《岩土工程勘察规范》（GB 50021—2001）中定义了盐渍土的含盐量界限值为0.3%，结合本次试验设定盐溶液浓度C为0%、0.3%、1.0%、5.0%、8.0%，即先用纯净水配制饱和NaCl溶液，并定义其饱和状态下的溶液初始浓度为100％，后续则对溶液样品进行稀释得到所需浓度。其次根据烘干法测得红黏土的天然含水率为31.9%，据此分别设置测试土样的含水率$\omega$为20%、25%、27%、30%、33%。最后在制备试样的过程中，以最大干密度为限，根据式(6)^[24]，即可通过控制干土的质量得到不同的孔隙率，制备了5种不同的干密度，分别为1.52、1.49、1.44、1.38、1.33 g·cm⁻³，即对应的孔隙率n为0.45、0.46、0.47、0.50、0.52。在此次试验中共配制了125 种土样。

式中：${m_{\text{s}}}$为干土质量，g；V为米勒盒体积，cm⁻³；G_s为土粒相对密度，g·cm⁻³。在此次试验中通过比重瓶法测量其为2.74 g·cm⁻³。

本次测量试样电阻率的四极装置主要为由亚克力材料制作而成的Miller Soil Box，如图2(a)所示，其尺寸为19.5 cm×2.9 cm×3.2 cm。将上述配制好的土样分别填入该装置中，得到部分试样如图2(b)所示。其中装置的两侧利用铜片作为供电电极A、B，中间的测量电极M、N则由铜丝组成，间距为6.5 cm。通过WDJD-4多功能数字直流激电仪（WDJD-4，重庆奔腾数控技术研究所有限公司）测量试样的电压及电流值，即可根据式(5)计算该试样的电阻率值，其中测量过程如图2(c)所示。

图3所示结果为试验过程中各含水率下部分土样电阻率随NaCl浓度变化的情况，其中图3(a)~(d)所属的含水率ω分别为20%、25%、27%、30%。由图可知，在各种含水率、孔隙率条件下，土体电阻率与NaCl浓度均呈负相关，即土体电阻率随着浓度的增大而降低，且在浓度开始增大时的初始阶段，电阻率下降趋势明显，而当浓度增大到一定值后，电阻率的下降趋势逐渐变缓。如以ω=20%、n=0.45的试样为例，当溶液浓度由0%增大至0.3%时，电阻率则由491.25 Ω·m降至53.40 Ω·m，降比达89.13%。而当溶液浓度继续增大至1%时，电阻率也继续降至12.99 Ω·m，降比为75.67%。通过曲线拟合的方法可以对其进行分析，得到NaCl浓度与电阻率之间的函数关系。以ω=20%和27%为例，拟合结果如表2所示，可知其电阻率与NaCl浓度的一次方程呈倒数相关，且相关系数在0.999 5~0.999 8之间，拟合效果较好。

分析出现上述现象的主要原因是因为在一定含水率情况下，当土体受到NaCl污染后，土体中的黏土矿物会吸附NaCl溶液中的导电离子，并随着浓度的增大，使得孔隙液中的导电离子数增多，从而土体的导电性增强，即只要土体一旦受到NaCl污染，即可引起电阻率的显著变化。然而当黏土矿物表面的吸附位逐渐达到饱和状态后，减弱了对导电离子的吸附能力，进而降低了导电离子的活动性，故而当NaCl浓度再增大时，电阻率的减小趋势也逐渐趋于平缓。

含水率是影响电阻率变化的重要因素，其在各NaCl浓度下电阻率与含水率之间的变化关系曲线如图4所示，其中图4(a)~(d)所属的NaCl浓度C分别为0%、0.3%、5%、8%。从图4可以得出，未污染土（C=0%）和其他3 种NaCl溶液浓度污染下的土体电阻率均随含水率的增大而降低，并且先剧烈减小，当含水率增大到一定值时，电阻率减小的趋势就开始逐渐趋于平缓。以C=5%、n=0.50时的试样为例，当含水率由20%增大至25%，再继续增大至30%时，电阻率则由9.78 Ω·m降至1.39 Ω·m，再降至0.80 Ω·m，在这2个含水率区间段，降幅则由85.79%降为42.45%。同理，对所得数据结果进行拟合，以C=0%、5%为例，其结果如表3所示。从拟合结果可以看到土体电阻率与含水率基本呈幂函数关系，拟合相关系数都在0.924 3~0.996 1之间，这也说明了幂函数关系拟合的效果较好。

在非饱和土中，电流的传播通道有3条，即沿孔隙水中、土颗粒之间以及土颗粒-水相连接而成的通道间^[25]。当土体完全干燥或含水率较低时，土体中的电流主要通过相接触的土颗粒之间来传播，故其电阻率较高，当含水率增大，土体孔隙中逐渐被溶液填充，增大了土颗粒-水相间的路径及孔隙水之间的传导作用，增强了土体中的导电能力，从而电阻率减小。当含水率继续增大，使得土体中的孔隙几乎都被溶液所充填，增大了孔隙液间的连通性，这时土体中的孔隙水导电占据主导作用，继续增大含水率时，其电阻率降低幅度较之前会变得不明显，最终逐渐趋于土体中孔隙水的电阻率。

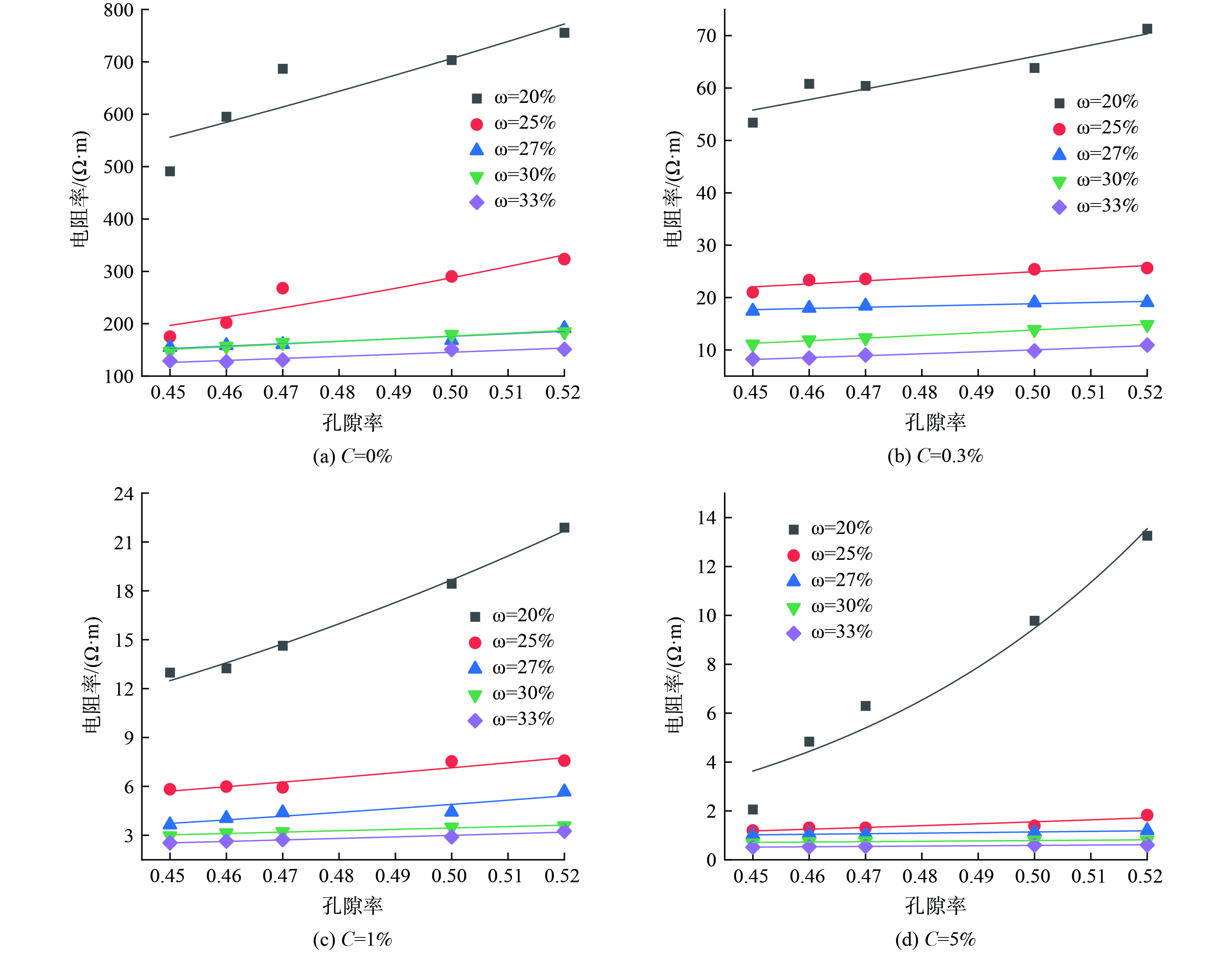
孔隙率是表征土体密实度的物理指标，图5则为各NaCl浓度下电阻率与孔隙率之间的变化关系曲线，其中图5(a)~(d)所属的NaCl浓度C分别为0%、0.3%、1%、5%。由图5可知，在不同NaCl浓度、不同含水率条件下，土体电阻率与孔隙率呈正相关，且随孔隙率的增大而增大。以C=0.3%，ω=25%和30%时的两组试样为例，当孔隙率均由0.45增大至0.52时，电阻率则由21.02、11.09 Ω·m分别增大至25.63 Ω·m和14.83 Ω·m，即分别增大了4.61、3.74 Ω·m。对数据进行拟合分析，以C=0%、5%为例，其土体电阻率与孔隙率的关系表达式如表4所示，可以看出土体电阻率与孔隙率仍呈幂函数关系，拟合相关系数在0.729 1~0.967 0之间。而拟合的相关系数在0.8以上则可以认为拟合程度较好，从表4的拟合结果来看，仅有2条拟合曲线的相关系数在0.8以下。其原因可能是在试验的过程中由于人为操作不当或仪器等导致测量的数据有一定误差。

分析其原因主要是在其他条件一定的情况下，当孔隙率较小时，土体较密实，孔隙水以及土颗粒间的连续性较好，即导电路径贯通性强，且导电通道增多，因此电阻率较小，而随着孔隙率的增大，土体逐渐变得相对疏松，粒团间的距离增大，导致孔隙水以及土颗粒间的连续性变差，导电路径减少，且电流传导路径变长，故其电阻率增大。

正交试验通过对各因素的各种水平进行均衡搭配，从而能够以较少试验次数的结果掌握全面的试验情况，具有高效、省时等特点^[26]。

本次设计了3因素3水平的正交试验，用以探讨NaCl浓度（A）、含水率（B）、孔隙率（C）这3 种因素对土体电阻率的影响主次。正交试验设计与计算结果如表5所示，表中K₁、K₂、K₃分别代表三个因素的1、2、3水平所对应的试验结果之和，k₁、k₂、k₃分别是K₁、K₂、K₃的平均值，R为极差，由各列k的最大值减去最小值所得。这3 种因素对土体电阻率的影响主次即可通过极差R的大小来判断，极差越大，说明土体电阻率受该因素的影响也最大。

由表5可知，因素A、B、C的极差（R_A、R_B、R_C）分别为25.51、20.91、7.30，即R_A>R_B>R_C，故NaCl浓度对土体电阻率的影响最大，含水率次之，孔隙率则对土体电阻率的影响最小。

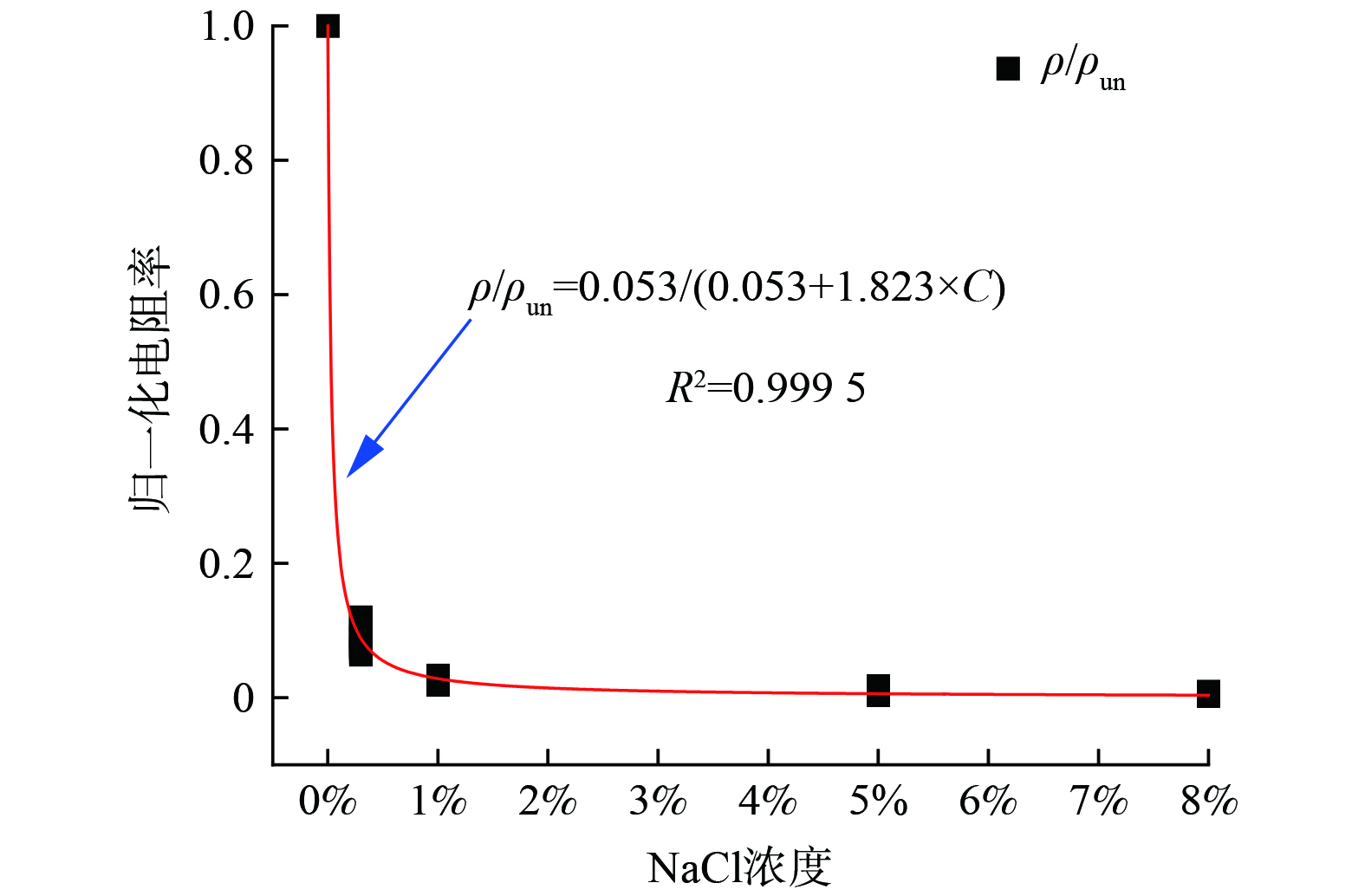
为建立NaCl污染土电阻率$\rho$与未污染土电阻率${\rho _{{\text{un}}}}$之间的关系，以25 种未污染土的电阻率为基数，将与之对应的不同NaCl浓度下相同含水率、孔隙率的电阻率进行归一化处理分析。并基于前面的NaCl浓度对电阻率影响的分析结果，建立归一化电阻率$\rho /{\rho _{{\text{un}}}}$与NaCl浓度的相关关系，其结果如图6所示。

在图6中，通过对归一化电阻率的拟合结果可知，$\rho /{\rho _{{\text{un}}}}$与NaCl浓度呈负相关，即$\rho /{\rho _{{\text{un}}}}$随着NaCl浓度的增大而减小，且先急速下降，再逐渐变缓，其二者之间的拟合关系式如式(7)所示。

前面已经得到了$\rho$与${\rho _{{\text{un}}}}$之间的拟合关系，并且由试验结果分析可知，未污染土的电阻率与含水率、孔隙率之间均呈幂函数的关系变化。在此，本研究为了更好的将含水率和孔隙率与电阻率之间的关系联系起来，引用体积含水率${P_{\text{r}}}$这一概念，即孔隙水体积V_w与土体总体积V之比，表达式如式(8)所示^[22]，且陈议诚等^[27]学者研究得出其红黏土电阻率与体积含水率仍呈幂函数关系。

式中：V_v为孔隙体积；S_r为土的饱和度；G_s为土粒相对密度。

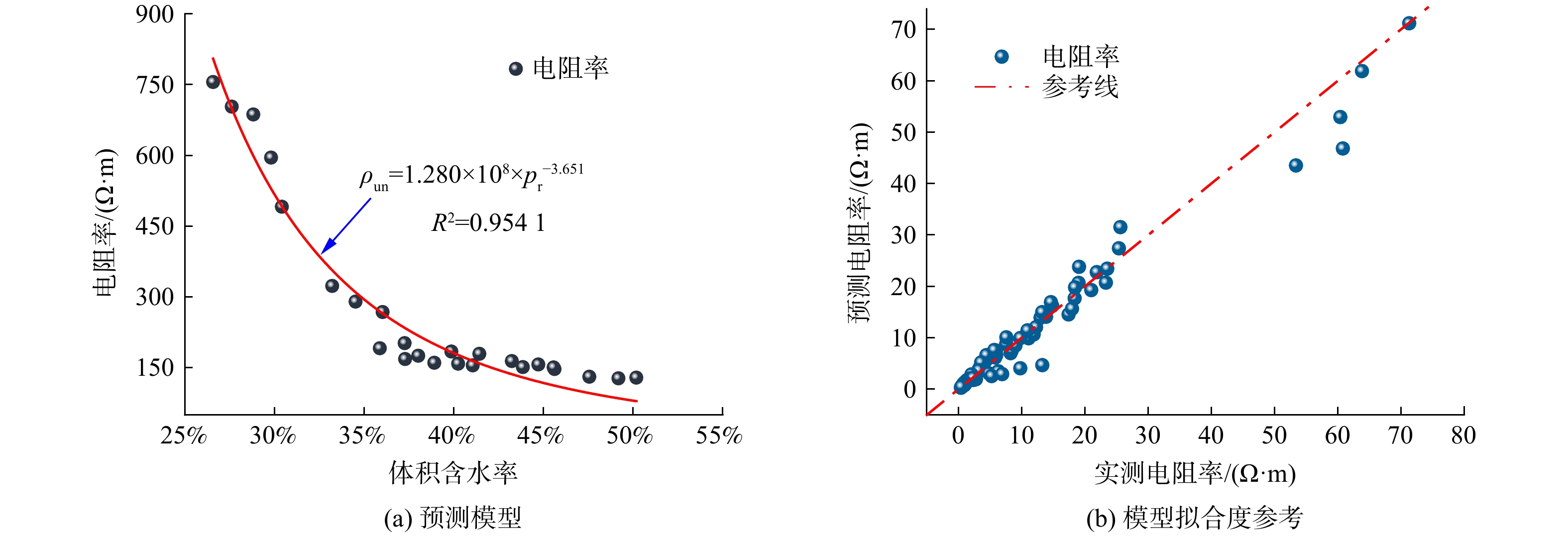
基于前述的Archie电阻率模型能够建立未污染土电阻率与体积含水率的函数。通过对25 种未污染土试样进行体积含水率计算后，构建其未污染红黏土电阻率${\rho _{{\text{un}}}}$与体积含水率${P_{\text{r}}}$间的函数关系，如图7(a)所示，其拟合函数如式(9)所示。

将式(9)代入式(7)即可得到盐渍红黏土电阻率预测模型，表达式如下。

最后，通过将以上预测模型计算得到的电阻率值与试验实测电阻率值进行对比分析，如图7(b)所示，图中横、纵坐标分别为实测电阻率与预测电阻率，红点线（y=x）则为二者之间的参考线。若数据点越靠近参考线，则说明拟合效果越好，即建立的模型越准确。从图7(b)中可以看出，数据点是比较接近参考线的，证明建立的该盐渍红黏土电阻率预测模型能够较好地反映出电阻率与NaCl浓度、含水率及孔隙率之间的关系，在一定程度上可用于NaCl污染红黏土的定量评价。

1）盐渍红黏土电阻率与NaCl浓度的一次方程呈良好的倒数关系，而与含水率、孔隙率间则均呈良好的幂函数关系。其中电阻率随着孔隙率的增大而增大，而随着NaCl浓度、含水率的增大，电阻率则减小。

2）基于3因素3水平的正交试验，通过极差法来判断这3 种影响因素对盐渍红黏土电阻率影响的主次顺序，其结果为：NaCl浓度影响最大、含水率次之，孔隙率最小。

3）通过对NaCl浓度、含水率及孔隙率的综合分析，构建了基于这3 种主要影响因素共同作用下的盐渍红黏土电阻率预测模型。并根据该模型计算得到的预测电阻率值与实测电阻率值之间的吻合性较好，故而通过该模型能够为NaCl污染红黏土区域的污染程度判定提供一种评定方法。