-
电除尘器作为工业烟气净化的主要设备之一,由于其总除尘效率高、本体阻力低、处理烟气量大、耐高温强腐蚀性气体以及运行维护费用低等优点,广泛应用在电力、冶金、建材等工业领域[1]。理论上,电除尘器可以高效捕集任何粒径的气溶胶粒子,但在实际工业应用中,对亚微米粒子和超细粒子(粒径小于0.1 μm)的捕集效率并不理想[2-5]。为了提高电除尘器对细颗粒物的捕集效率,开发新型电极电除尘器是采取的主要措施之一[6]。基于电风效应对细颗粒物运动状态的影响,减缓收尘电极附近的湍流现象,提出的多孔收尘电极电除尘器是其中之一,其电极结构特征是多孔板型式的收尘极板,在较低的比集尘面积条件下,对细颗粒物有较高的捕集效率。为引导该新型电除尘器设计选型,研究微细颗粒物在其电场内部沉降过程与除尘性能尤为重要。
由于对电除尘通道内各种电气、流动和粒子参数进行实测存在困难,数值模拟方法广泛应用在电除尘器通道内电气特性、流场特性和粒子运动特性的研究。GAO等[7]利用数值模拟方法描述双区电除尘器的物理过程,通过实验验证了该数值模型的准确性,并建立了双区电除尘器除尘性能与影响因素之间的定量关系。DONG等[8]对尖端放电极形式的电除尘器进行了气固两相流的数值研究,详细分析了进口气流速度、负电晕电压、放电极上的尖端位置对气流流线分布的影响。ZHU等[9]利用数值模拟方法研究了波型板电除尘器和平行板电除尘器中微粒的捕集过程,研究发现波型板电除尘器比平行板电除尘器具有更强的电场特性,并且对离子风流动具有更强的抵抗能力。目前,采用数值模拟方法对该新型电极电除尘器的研究内容鲜见报道,而且对其除尘性能及颗粒沉降规律尚不清晰。
多项研究表明,新型电极可从多方面提高电除尘器除尘性能。本研究采用数值模拟方法研究荷电粒子在多孔收尘电极电除尘器内迁移与沉降规律,并以平板电极为基础,结合多孔板电极利用数值模拟软件Comsol Multiphysics探究2种不同收尘极结构下电除尘器通道内的电气特性、流场特性和粒子运动特性,以揭示多孔收尘电极电除尘器的提效机理,并为该新型电极电除尘器的选型设计提供参考。
-
忽略尘粒与气体对电场影响,电场电晕放电控制方程可简化为泊松方程与电流连续方程[2],如式(1)~式(4)。
式中:E为电场强度,V∙m−1;J为电流密度,A∙m−2;φ为电压,V;ε0为真空介电常数,8.85×10−12 C2∙(N∙m2)−1;μion为离子迁移率,m2∙(V∙S)−1;Dion为离子扩散系数,m2∙s;ρion为空间电荷密度,C∙m−3;uf为流体速度,m∙s−1。
-
电除尘器内的流场被称为电流场,含有大量气体离子电荷与颗粒荷电后电荷,流体本身也受电场力作用,已有研究[10-13]表明,采用时均Navier-Stokes方程和雷诺应力标准湍流模型[14]对电除尘器内电流场可进行有效的求解。时均Navier-Stokes方程与标准κ-ε湍流模型可以写成式(5)~式(10)。
式中:uf为流体速度,m∙s−1;ρf为流体密度,kg∙m−3;p为气体静压,Pa;μ为层流黏性系数,kg∙(m∙s)−1;μT为湍流黏性系数,kg∙∙(m∙s)−1;I为单位矩阵;湍流动能κ与湍流耗散系数ε;Pk为湍动能每单位耗散净产出。常数分别为:Cμ=0.09,σκ=1.00,σε=1.30,Cε1=1.44,Cε2=1.92。
-
电除尘器中粒子荷电有2种荷电机制:电场荷电与扩散荷电[2]。龙正伟等[15]从计算精度和计算效率两方面分析使用Lawless[16]模型模拟粒子荷电过程满足计算需求。因此,颗粒的总荷电速率可以表示为式(11)~式(17)。
式中:kB是玻尔兹曼常数;Tion是离子温度;Rf和Rd是无量纲场荷电率及扩散荷电率;εrp为粒子的相对介电常数;fa是联系电场荷电率与扩散和电率的一个功能函数公式(18)。
-
描述颗粒运动方法有欧拉模型与拉格朗日模型,前者适合计算宏观的运动,而后者适合研究单颗粒的运动。本研究为了解多孔电极电除尘器内部单颗粒的运动特性,采用拉格朗日运动模型对粒子沉降规律进行描述。进入电除尘器的颗粒在荷电后受到电场力作用,同时受到曳力及重力作用。对电除尘器进行二维模拟,忽略颗粒在竖直方向受到的重力,由牛顿第二定律,颗粒的运动方程见式(19)。
式中:up是颗粒运动速度,m∙s−1;uf是流体运动速度,m∙s−1;CD是流体曳力系数;ρp是颗粒密度,kg∙m−3;dp是颗粒直径,m,q是颗粒荷电量,C;流体曳力系数CD是颗粒雷诺数Rep的函数,满足公式(20)[17]。
式中:Rep表示气流中颗粒运动特征的无量纲准数,可由式(21)计算[18]。
式中:Cc为肯宁汉修正系数,计算方法[19]如式(22)~式(23)所示。
式中:dp为粒子直径,m;kB为玻尔兹曼常数,1.38×10−23 J∙K−1;T为气体温度,K;p为气体压强,Pa;d为气体分子有效直径,干空气分子有效直径约为3.70×10−10 m;λ为气体分子平均自由程,在1个大气压和20 ℃条件下约为6.60×10−8 m。
-
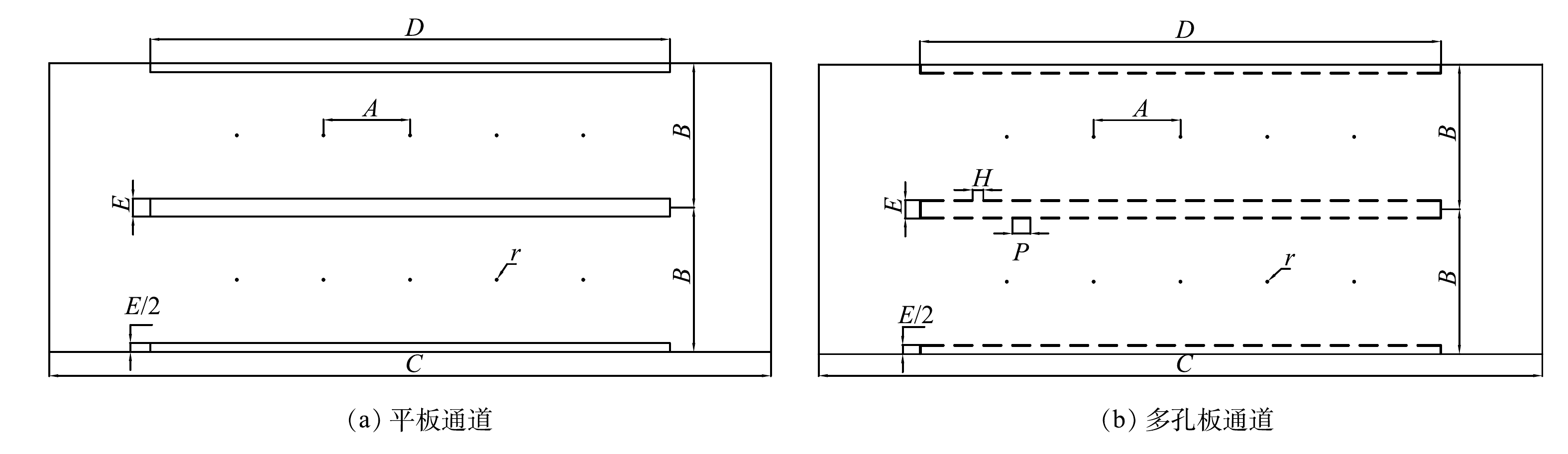
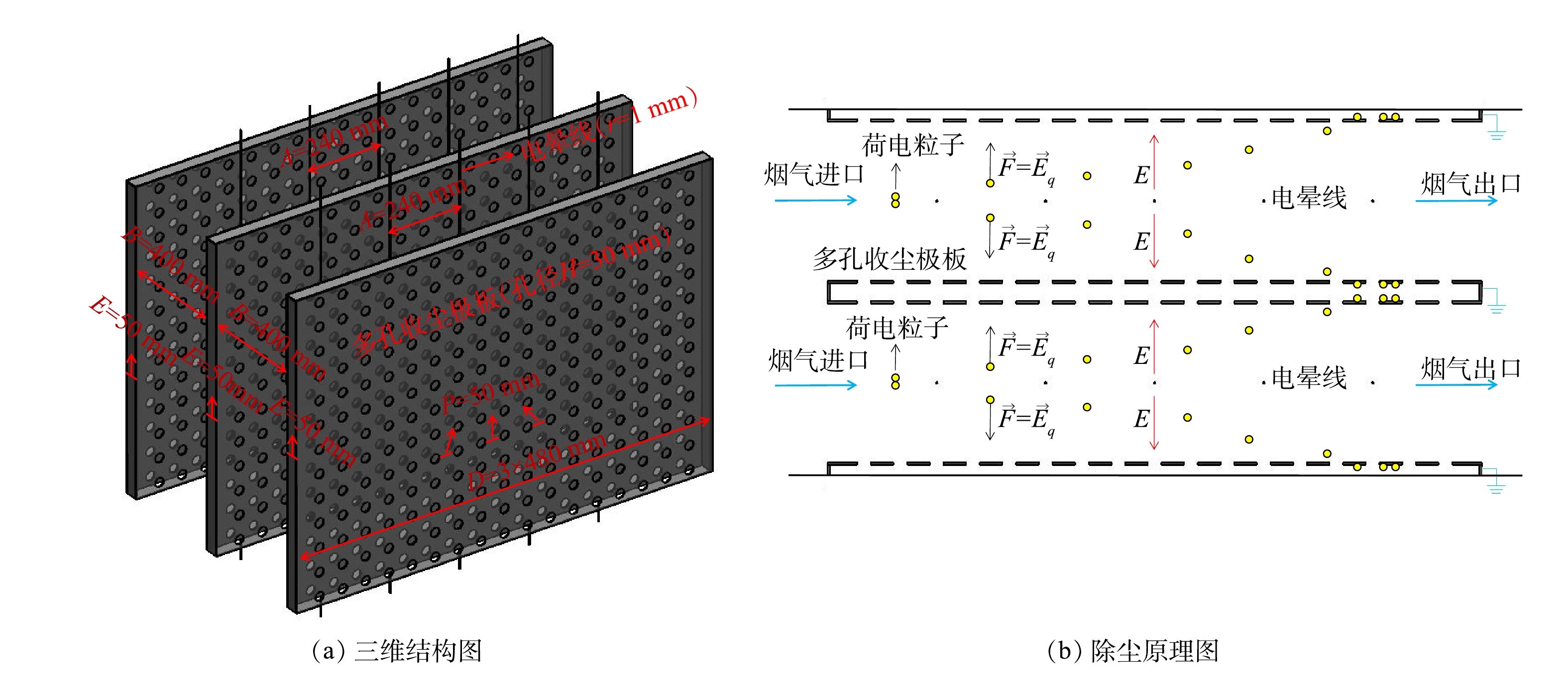
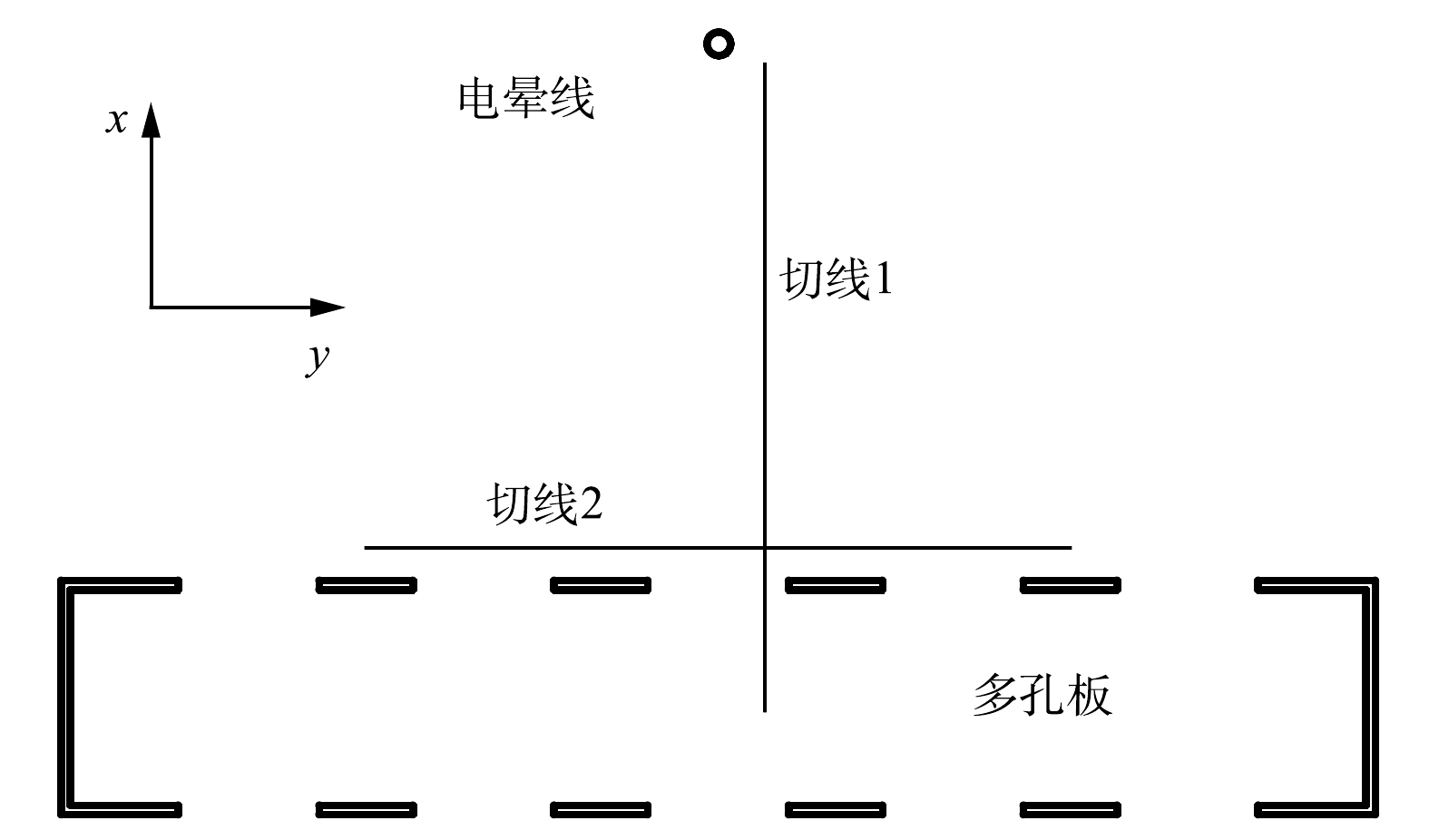
为指导该新型电除尘器设计选型,多孔电极几何尺寸按照工业电除尘器电极尺寸构建。由于电除尘器中微细颗粒重力可以忽略不计[2],故采用电除尘器除尘部分二维特征结构。本研究以平板电极电除尘双通道为参照,分析多孔电极对微细颗粒物的提效机理,通道中相邻5根电晕线及其周边区域为模拟区域。图1给出了2种收尘极板电除尘通道的剖面简图,圆孔在立面以相同的孔间距均匀分布,多孔在立面开孔率为17.2%。图2给出了除尘通道三维结构示意图与除尘原理图,通道基本尺寸与计算参数取值汇总在表1中。
电除尘器运行参数根据工业电除尘器的常见运行条件选择。外加电压为65 kV;入口气体流速为1.00 m∙s−1;流体温度293.15 K;密度1.24 kg∙m−3;层流粘性系数为1.88×10−5 kg∙(m∙s)−1;入口释放颗粒个数为5 000个;颗粒密度2 200 kg∙m−3;相对介电常数为5。
-
电除尘器模拟采用的边界条件汇总在表2。其中,电晕极表面的电势为运行电压,离子空间电荷密度根据Kaptzov假设[20]并结合Peek定律[21]来调整,由此计算得到的场强值等于表面场强大小。
-
由于几何模型曲率半径相差较大,对模型采用三角形网格单元离散化。电晕线和收尘板附近的网格被细化,其中电晕线表面网格最大尺寸为0.2 mm;收尘板表面网格最大尺寸为2 mm。计算域中的最大单元尺寸为20 mm;平板电极结构有77 124个域单元;多孔板电极结构有174 844个域单元,对计算域网格进行收敛测试以确认网格大小符合计算要求,可以获得独立于网格的数值解。
-
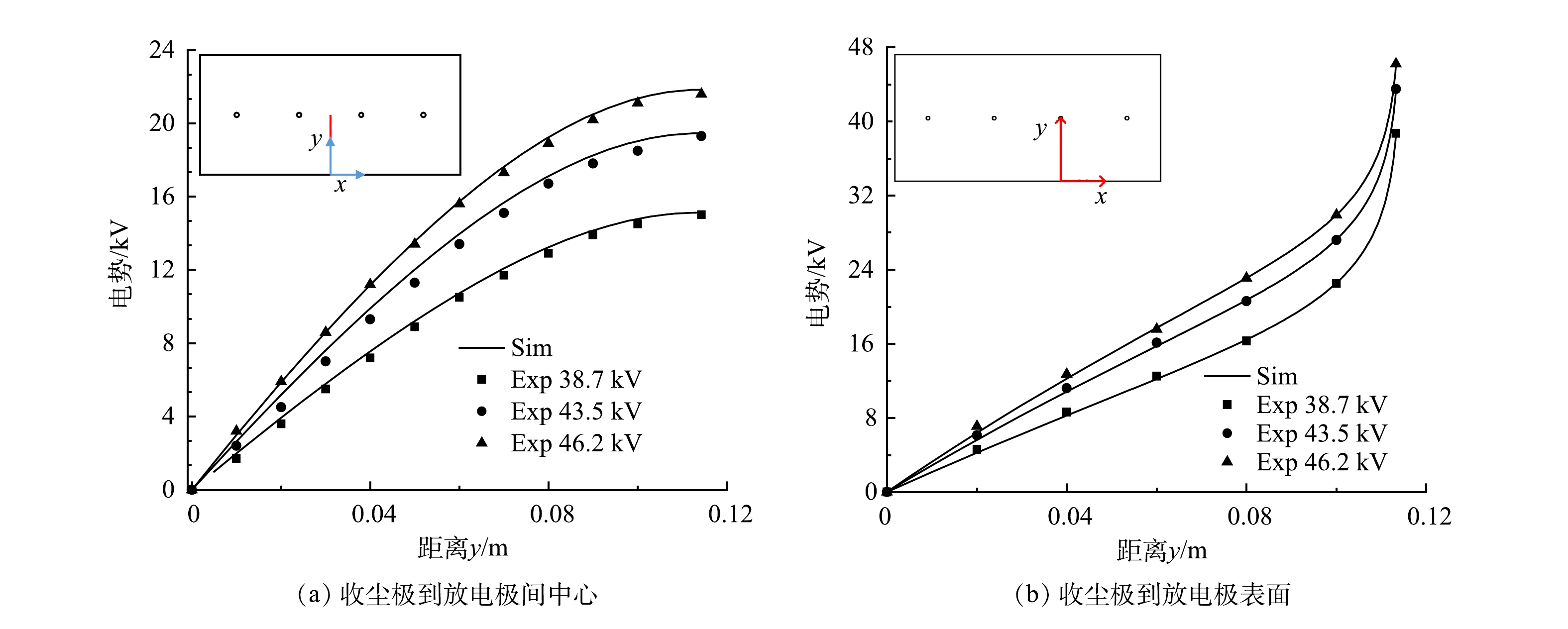
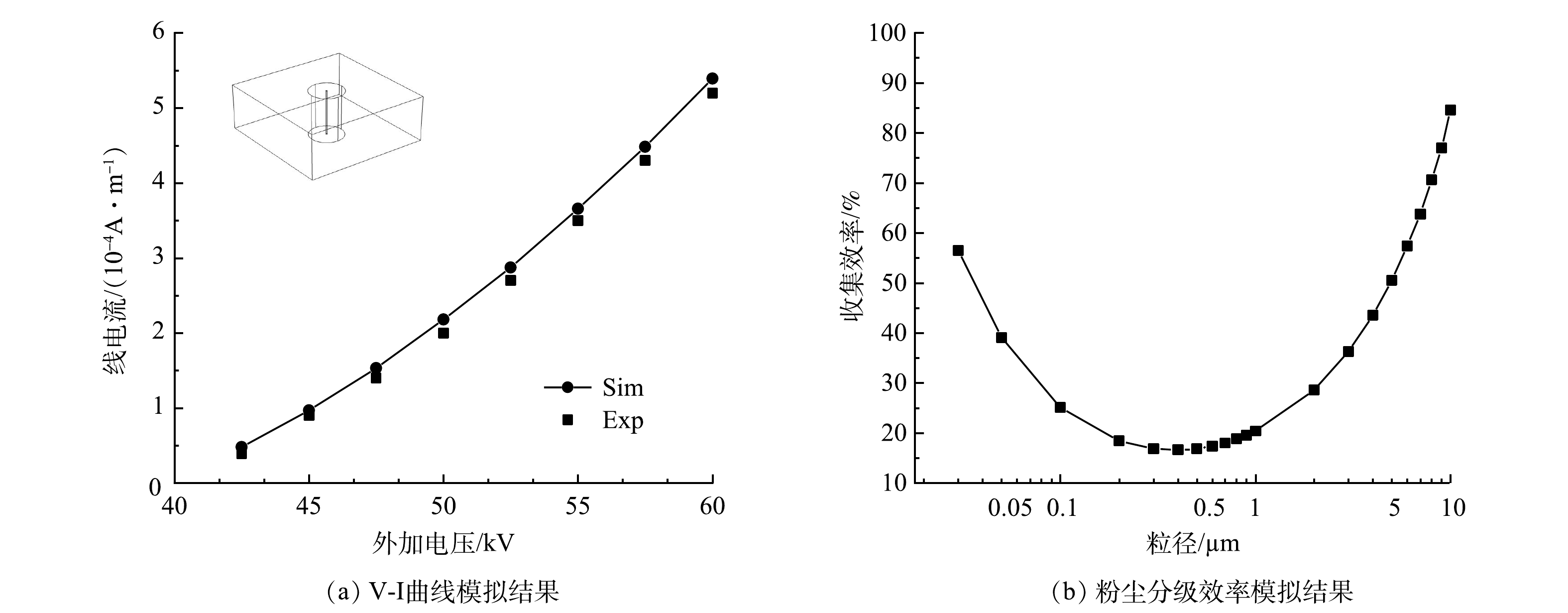
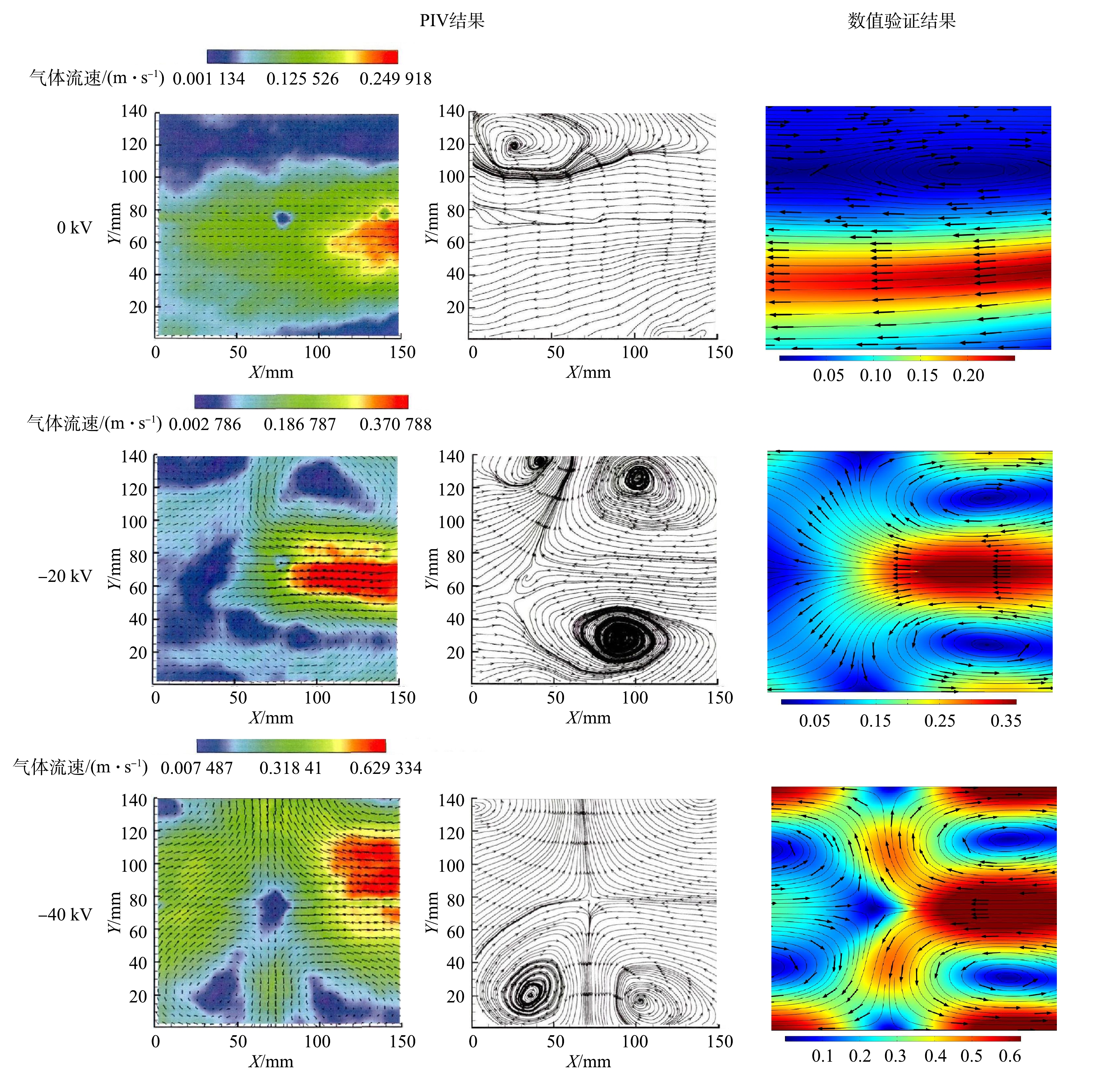
为了验证数值模型的准确性,将模拟结果与多组实验数据进行对比,其中极间电势分布验证按照Penny、Matick实验模型[22]建立电场通道长为0.609 6 m;板间距0.228 6 m;线间距0.152 4 m;线径1.016 0 mm几何模型。伏安曲线验证按照Lawless、Sparks实验模型[23]建立极板尺寸0.228 6 m×0.100 0 m;板间距0.228 6 m;线径为1.590 0 mm几何模型。电流体验证按照文献[24-25]实验模型建立断面尺寸200 mm×200 mm;极板尺寸400 mm×200 mm;板间距200 mm;电晕线直径为0.150 0 mm几何模型。图3给出了外加电压为38.7、43.5、46.2 kV时数值计算结果与Penny、Matick电势分布实验数据对比。图4(a)为实验条件为温度615 K;压力0.86 atm;外加电压处于42.5~60 kV的V-I曲线模拟结果与Lawless、Sparks实验数据对比。图4(b)为粉尘分级效率捕集曲线。图5给出了实验条件为室温22 ℃、相对湿度约为50%、气体流速为0.200 m∙s−1时,外加电压分别为0、−20、−40 kV时电流体模拟结果与PIV实验结果的对比。
图3和图4(a)的结果表明,本研究的数值结果与实验得到的结果符合较好,且所选择的静电模块和稀物质传递模块可以对电场和空间电荷进行准确的描述。图4(b)的粉尘穿透曲线与众多研究者的结果[5]一致,在0.1~1 μm范围内会出现除尘效率的最低点,本研究对电除尘器粒子的收集效率预测具有准确性。图5电流场计算结果与PIV实验结果基本一致,电流场计算模型与实验模型符合较好。
-
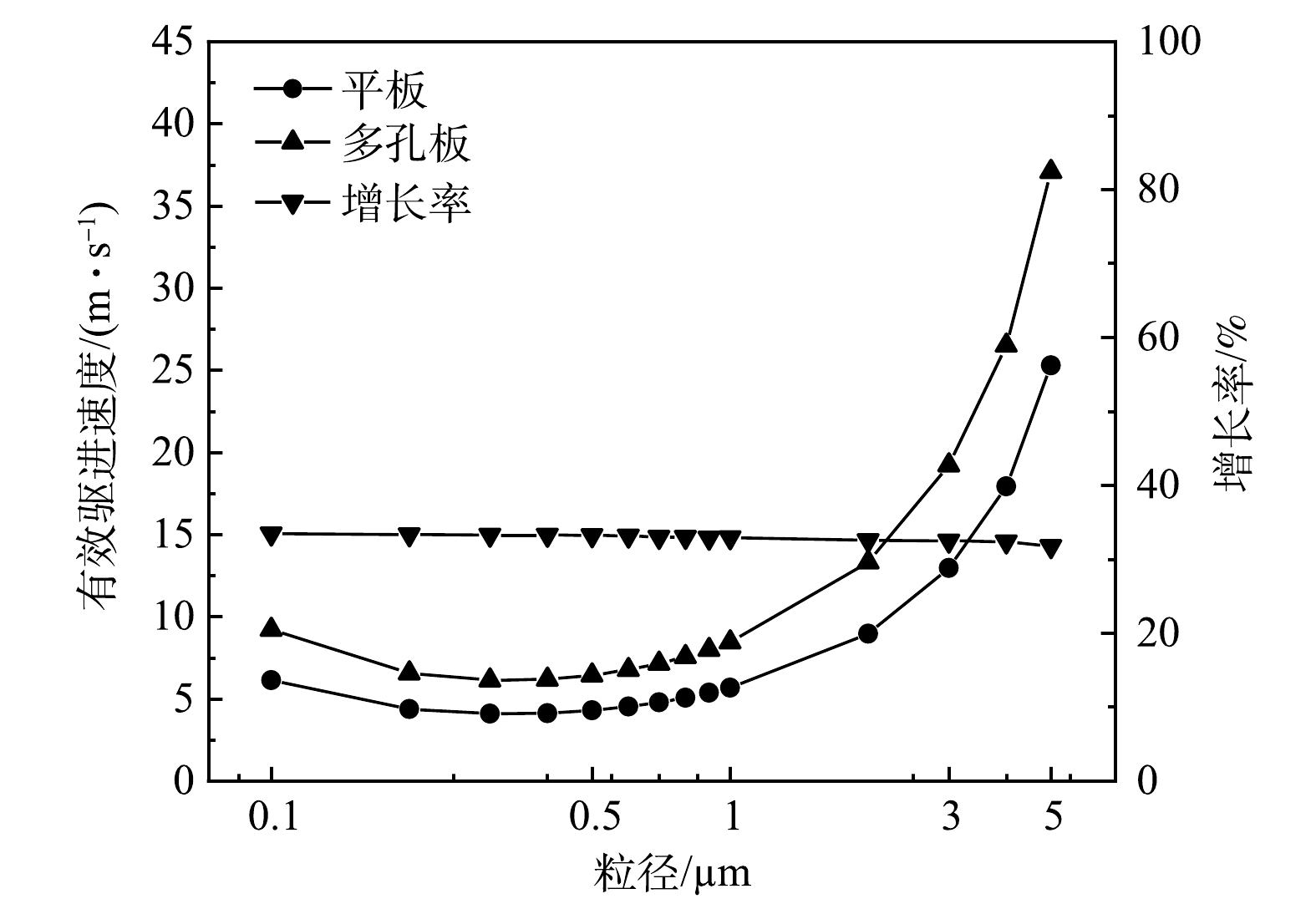
为探究极板开孔后对电除尘器除尘性能影响,对比分析了平板与多孔板电极中处于0.1~5 μm范围内颗粒的有效驱进速度,结果如图6所示。当粒径处于0.1~5 μm,2种电极结构下有效驱进速度随粒径变化的趋势一致,曲线均呈现马蹄形,最低点均在粒径0.3 μm处。这是因为,在0.1~1.0 μm范围内颗粒双荷电机制均处于下限,颗粒荷电量不高导致其受电场力作用有限,此时曳力引入肯宁汉系数所致。结果表明,多孔板电极中颗粒有效驱进速度较平板电极中颗粒有效驱进速度提升30%,在与平板电极结构几何尺寸相同的条件下,多孔板电极结构增大了收尘面积并提高微细粒子有效驱进速度,可降低电除尘器运行成本。
-
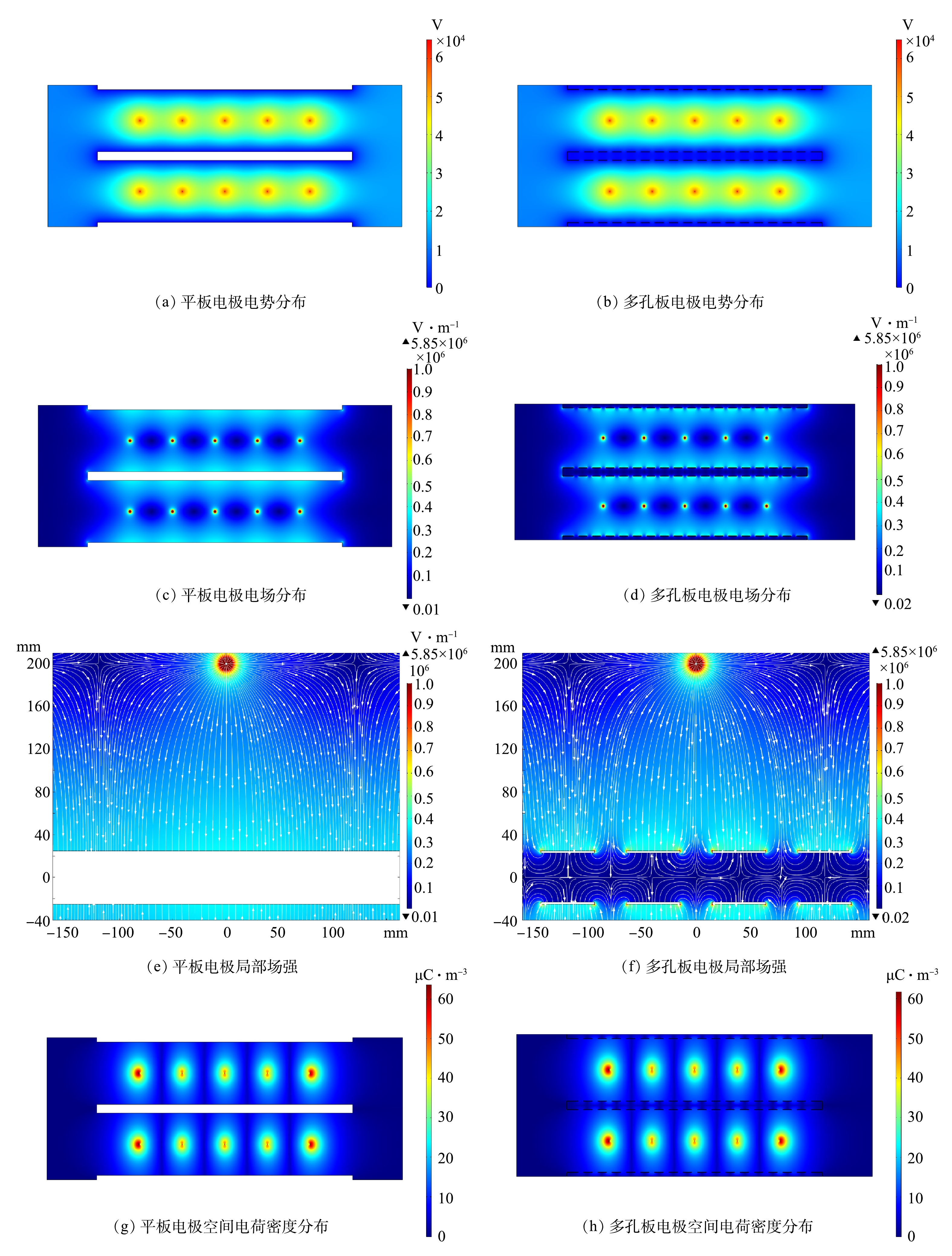
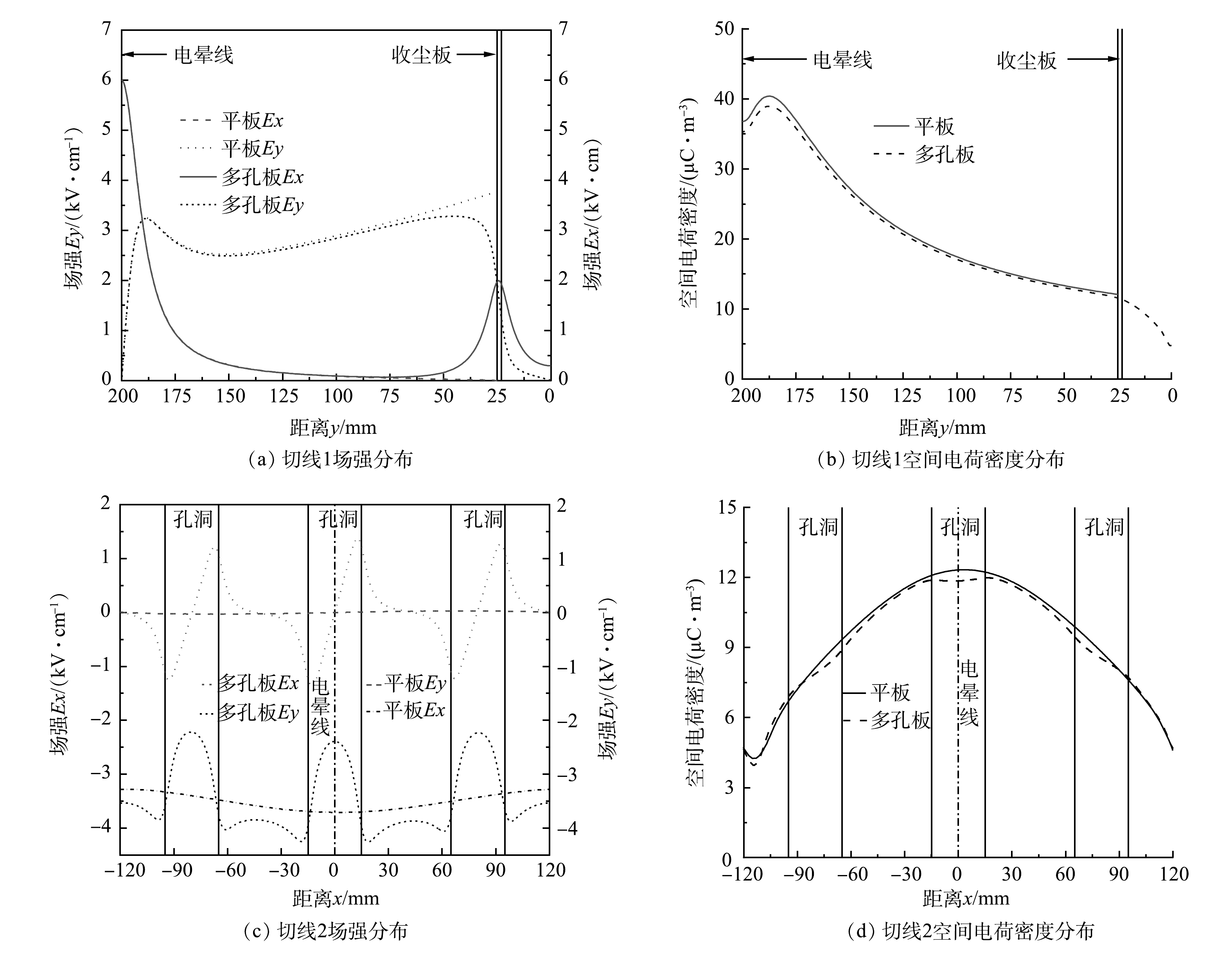
图7给出了2种板型下电气特性分布的数值结果,2种电极结构下的电势、电场强度与空间电荷密度分布相似,电势与空间电荷密度均在电晕线表面最高,远离电晕线时下降;电晕线表面的电场强度最大,电晕线表面至收尘极板,电场强度呈现先减小后缓慢增大的趋势,这与OGLESBY[26]描述结果一致。结果表明,收尘板表面电场强度随电晕线距离的减小而增大,圆孔只会影响多孔板附近的电场分布。根据图7(e)和图7(f)所示,板表面电场强度分布与导线和圆孔的位置有关,电场强度在孔边缘达到最大值,电场穿过圆孔分布在多孔板的背面区域,背面区域的电势、空间电荷密度和电场强度随远离多孔板而迅速降低。
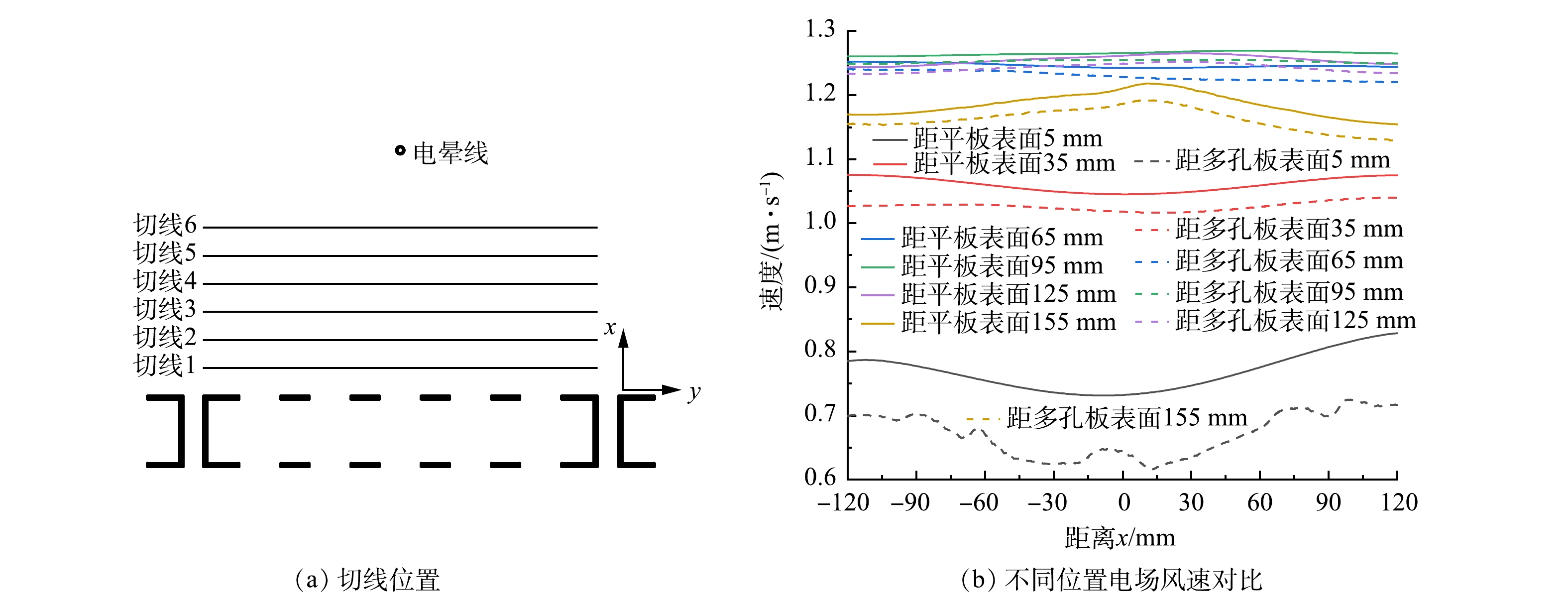
如图8所示,选取2条切线上的电场数据作定量分析。其中,切线1位于x=10 mm,穿过圆孔距离多孔板实体截面右侧边缘5 mm处;切线2位于y=30 mm,距离多孔板实体截面5 mm处。根据图9(a)与图9(b),2种电极结构沿切线1空间电荷密度分布曲线在线板间区域重合,场强延伸曲线在大多数区域重合,但在收尘板附近存在不同,电场竖直分量Ey减小,水平分量Ex增大,并在圆孔位置处电场水平分量Ex出现最大值,进入多孔板背面后迅速减小。以上结果表明,圆孔显著提高了电场通道中距板表面25 mm内电场强度。
图9(c)与图9(d)比较了2种电极沿切线2的电场特性分布,圆孔对空间电荷密度分布并无影响。平板结构下Ex接近于零,而多孔结构下Ex存在以孔间距为周期的波动,振幅约为3.00 kV·cm−1,接近电晕线时振幅略微增加。Ex在圆孔左、右边缘处分别达到最小值与最大值,在圆孔和板实体截面中心为0,Ex通过板实体截面中心或圆孔中心时改变方向,方向总是指向板实体截面最近的中心位置。以上结果表明,在与板面相邻区域中,Ex具有相同的特性,这有助于颗粒在多孔板三个侧面上沉积。在平板电极结构下,与电晕线相对的板表面处Ey有最大值,随远离电晕线减小,平均值为3.51 kV·cm−1;收尘板开孔后,圆孔位置的Ey减小,而多孔板实体截面的Ey增加,平均值为3.42 kV·cm−1,多孔板附近的电场强度因开孔而增加。
-
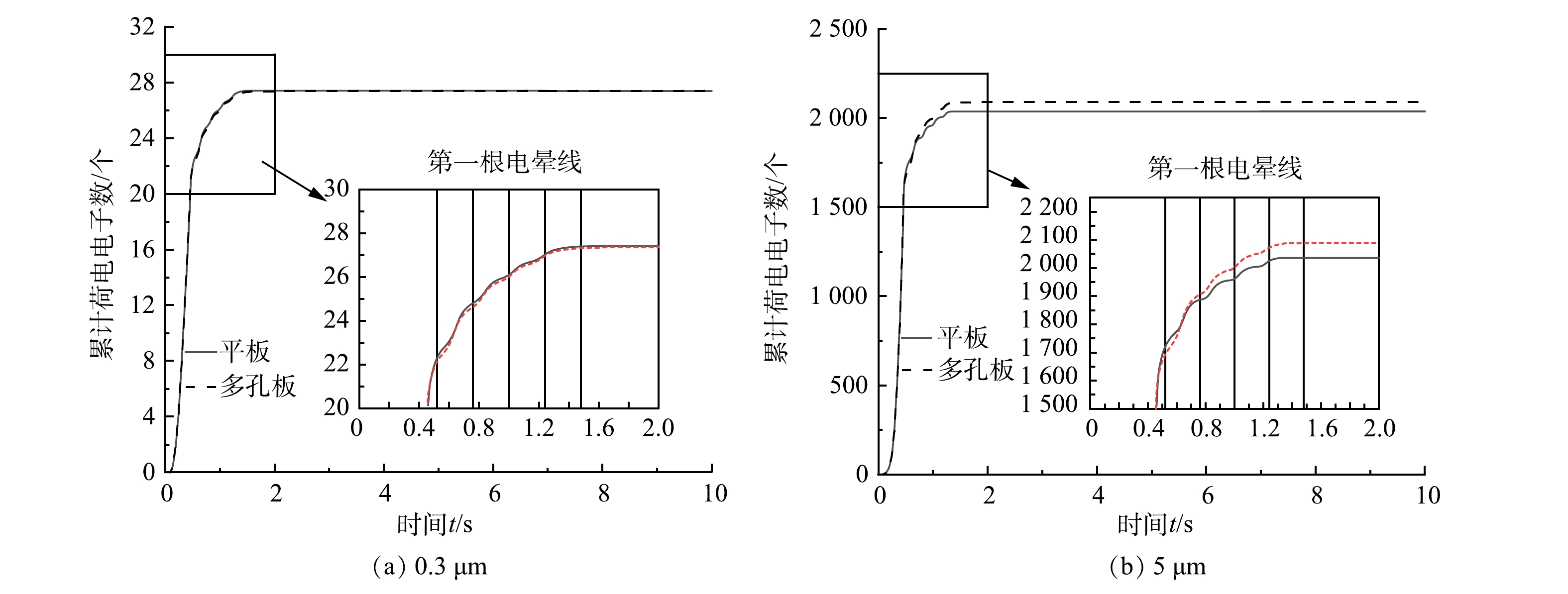
模拟结果表明,2种板型通道内0.1~5 μm粒径的粒子荷电总数相近,荷电总数增长趋势在1 μm左右发生突变,这与粒子荷电机制有关[27-28]。由于电场中离子电流引起的粒子荷电过程随粒子直径减小而使其荷电有效性降低,对于粒径大于1 μm的颗粒由电场荷电起主导作用;当粒径处于0.1~1 μm范围内,颗粒由电场荷电和扩散荷电共同作用,电场荷电不再起主导作用。电场荷电粒子的饱和荷电量与颗粒粒径的平方成正比,因而当颗粒粒径处于1 μm时,粒子荷电总量发生突变。
图10比较了0.3和5 μm颗粒的粒子荷电过程,粒子自进入通道内至第1根电晕线位置的0.5 s内,获得荷电总量80%左右电荷。这是由于,粒子靠近电晕线,场强增加使粒子开始快速荷电;当粒子远离电晕线时,场荷电速率降低;场荷电停止时,粒子进行扩散荷电。粒子所得电荷越高,使得离子与粒子间的库仑力增大产生排斥,离子很难扩散到粒子表面,此时粒子达到最大电荷量。粒子最终电荷量与其直径相关,5 μm粒子最终电荷荷电量是0.3 μm粒子的43倍。平板电极中0.3 μm粒子平均需要1.68 s获得27.408个电荷达到饱和电荷量,多孔板电极中0.3 μm粒子需要8.47 s获得27.409个电荷达到饱和电荷量,这表明多孔板电极延长了粒子最终荷电时间,但并不影响粒子荷电总量。
-
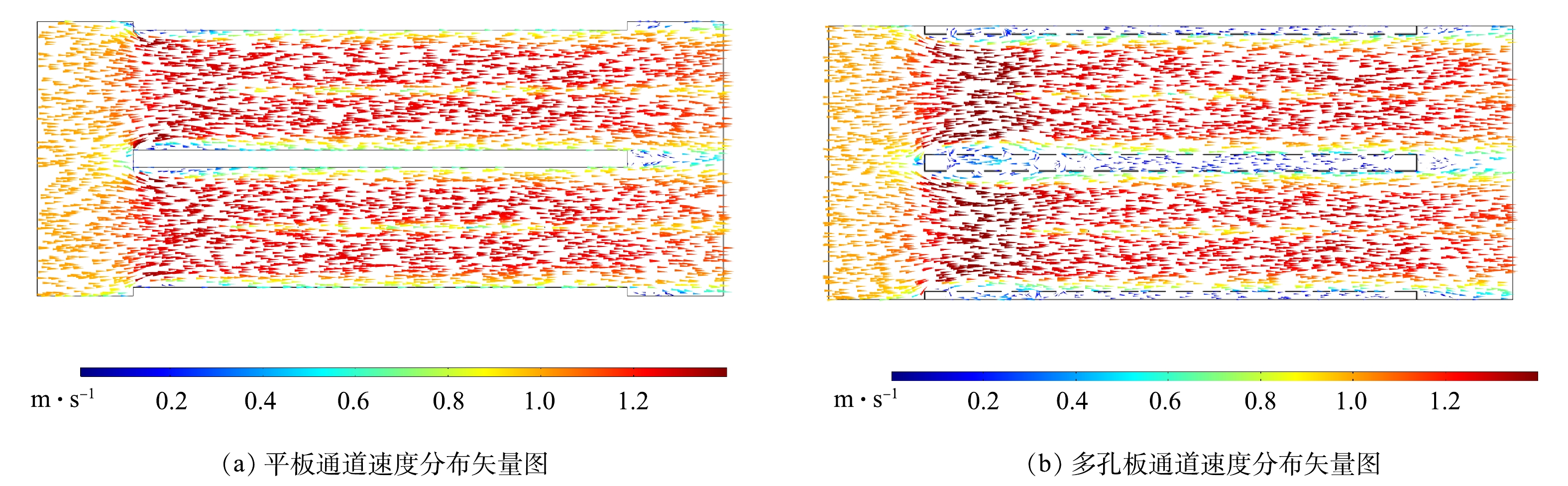
图11是2种板型下通道内速度分布矢量图,流场结构分布在大部分区域相似,但在收尘极板前端和尾端出现了阻流和气流死区现象,这是由于几何模型考虑了收尘极板厚度所致。在多孔板结构下,部分气流会进入多孔板空腔内部,由于空腔内气流流速较低,可增加粉尘在电场内的停留时间从而提高除尘性能。
如图12(a)所示,选取几何模型中心位置多孔板表面5、35、65、95、125、155 mm处的切线对流场进行分析。据图12(b)显示,2种结构通道内电场风速差别不大,靠近电晕线处的电场风速水平分量较高,远离电晕线后降低,但多孔板表面水平方向电场风速小于平板表面水平方向电场风速,板表面5 mm处相较于平板结构降低了12.5%。这是由于极板开孔后,相比于平板电极,通道内气流流通面积增大,在一定的气体流量下,降低了板面电场风速;同时,在通道进口处,多孔板结构对气流产生阻挡作用,气体流经孔板表面产生涡旋减弱了板表面电场风速。结果表明,多孔板可有效抑制二次扬尘的不利影响。
-
上述结果表明,粒子在2种板型板表面外区域的迁移沉降过程基本一致。选取了0.3和5 μm粒子在多孔板表面与空腔中的运动轨迹进行分析,结果如图13所示。图中绿线、红线、蓝线、灰线分别表示沉降在板正面、背面、侧面和逃逸颗粒的运动轨迹。由图13(a)和图13(b)可以看出,粒子被多孔收尘极板捕获可能性与进入通道内初始位置相关,粒子进入电场的位置决定粒子沉降的位置,入口距板表面较近的粒子更容易被捕集,未沉降至孔板的粒子最终随气流流出。由图13(c)和图13(d)可知,粒子运动轨迹整体可分为多孔板前端、中端和尾端,部分粒子在多孔板前端随气流运动形成涡旋,最终沉降至板表面。这是由于前端产生的局部阻流作用所致;位于中端的粒子随气流进入多孔板空腔,在电场力的作用下,粒子最终会沉降至多孔板空腔内背面与侧面;位于尾端空腔内的粒子部分随气流从圆孔流出沉降至多孔板表面。上述结果表明,多孔板解构改变了颗粒在极板附近沉降轨迹,颗粒会沉降至多孔板正面、背面与侧面,进入空腔内的颗粒不会再次返回通道内流出。
-
1)电除尘器气固两相流模型计算值与实验值吻合较好。
2) 极板开孔后不会对空间电荷密度与颗粒荷电过程产生影响,但会显著提高电场通道中距板表面25 mm内电场强度。
3)粒径范围处于0.1至5 μm内的粒子被多孔收尘极板捕获可能性与粒子进入通道内初始位置相关,被捕集的荷电粒子沉降在多孔板的正面、侧面与背面,随气流进入多孔板空腔内的粒子最终沉降在多孔板壁面上,不会再次返回电场通道内随气流流出。
4)模拟结果表明相较于平板,多孔收尘极板可增大板表面电场强度,减缓气流对收尘极板表面冲刷作用,并提高微细粒子的有效驱进速度,极板开孔后可以有效提高电除尘器的除尘性能。
多孔收尘电极电场中荷电粒子的沉降规律及其除尘性能预测
Sedimentation law of charged particles in electric field of porous dust collecting electrode and prediction of dust removal performance
-
摘要: 为了探究多孔收尘电极电除尘器的除尘性能,采用COMSOL Multiphysics建立电除尘器气固两相流数值模型,对多孔收尘电极电除尘器中的颗粒荷电沉降过程进行数值模拟,研究其电场、流场分布及粒子荷电、运动和沉降过程。结果表明,电除尘器气固两相流模型计算值与实验值符合良好。多孔收尘电极电除尘器能够有效提高微细粒子有效驱进速度约30%。极板开孔后显著提高了电场通道中距板表面25 mm内电场强度,开孔不会对空间电荷密度与颗粒荷电过程产生影响;多孔板结构表面5 mm处电场风速水平分量相较于平板结构降低了12.5%,消弱了气流对收尘区域的冲刷作用,进入多孔板空腔内的粒子最终沉降在多孔板壁面上。本研究结果可为多孔收尘电极电除尘器对微细粒子提效捕集的机理探究及新型电除尘器的选型设计提供参考。
-
关键词:
- 多孔收尘电极电除尘器 /
- 数值模拟 /
- 气固两相流 /
- 微细粒子 /
- 有效驱进速度
Abstract: In order to explore the dust removal performance of the Porous-dust-collecting-electrode electrostatic precipitators(PDCE-ESPs), COMSOL Multiphysics was used to establish a numerical model of the gas-solid two-phase flow of the electrostatic precipitators, and the particle charge sedimentation process in the PDCE-ESPs was numerically simulated in this study. The distributions of electric and flow fields and the charging, motion, and precipitation of particles in this specific structure were studied. The results showed that the calculated value of the gas-solid two-phase flow model of the electrostatic precipitators was in good agreement with the experimental value. The PDCE-ESPs can effectively increase the effective driving speed of fine particles by about 30%. After opening the plate, the electric field intensity within 25 mm from the plate surface in the electric field channel was significantly increased, and the opening had no effect on the space charge density and particle charge process. The horizontal component of electric field wind speed at 5 mm on the surface of porous plate structure decreased by 12.5% compared with that of flat plate structure, which weakened the scouring effect of air flow on dust collecting area, and the particles entering the cavity of porous plate eventually settle on the wall of porous plate. The results can explain the mechanism of the PDCE-ESPs for improving the trapping of fine particles, and provide a reference for the selection and design of the new type of electrostatic precipitators. -
垃圾收运是垃圾从产生到最终处理中必有的关键环节,且垃圾收运成本占垃圾处理总成本的50%以上[1]。如何对垃圾收运路径进行优化是城市及农村固废管理的重点难点之一。目前的垃圾收运路径往往只采用数学规划算法进行规划,以路径最短为唯一优化目标。但现实中,堵车、人流量、路面平整度、道路宽度、装车时间等实际因素造成了路况复杂多变[2],这种方法无法避免由复杂路况带来的垃圾收运成本高昂,同时对人居环境与自然生态造成了不可逆的负面影响。
启发式算法、元启发式算法、超启发式算法等仿自然体算法比追求精确结果的数学规划算法更适用于解决垃圾收运路径优化问题[3]。启发式算法在可接受的计算时间和空间下给出待解决组合优化问题每一个实例的一个可行解[4];元启发式算法不借助于某种问题的特有条件,从而能够运用于更广泛的方面[5];超启发式算法提供了某种高层策略,通过操纵或管理一组低层启发式算法,以获得新启发式算法[6]。其中,元启发式算法比启发式算法更不易陷入局部最优,而超启发式算法的研究处于起步阶段,尚未有成熟的应用。蚁群算法是元启发式算法的代表性算法,十分适用于解决垃圾收运类路线优化问题[7]。蚁群算法模仿了自然蚁群中蚂蚁返回时间最快的路径为最优路径的原理,还可以将从收集到处理中各环节的社会、经济、环境、生态、市政等多元数据也需要被纳入改进蚁群算法程序语言中。因此,对蚁群算法中的信息素更新规则、期望函数进行改进,可以有效减少垃圾收运成本及对周边人群健康与生态环境质量的不良影响。
本研究通过多元大数据融合、遥感数据可视化、多指标赋予权重、对传统蚁群算法加以改进,建立了垃圾从垃圾收集点到垃圾焚烧厂的收运路径优化模型,拟解决生活垃圾收运成本过高导致垃圾无害化程度较低的问题。
1. 材料与方法
1.1 研究区域
研究区域为我国东南部某县级市。该县级市总面积超过1
× × 研究对象为该县级市的其他垃圾,其处理方式为:先从垃圾收集点由垃圾收集车收集至经垃圾中转站进行压缩预处理后,然后由垃圾运输车运输至垃圾焚烧厂。经实际调研与网络查询,当地具有329个垃圾收集点、40个垃圾中转点、3个垃圾焚烧厂。
1.2 数据来源
本研究所需路网分布、道路长度、道路等级、道路限速等数据信息来源于Open Street Map网站的2020年全国路网矢量图[8],经过裁剪后得到研究区域路网图如图1所示。环境成本中包含的土地保护需求指标数据来源于500 m全球土地退化态势评价数据集[9],影响人口规模指标的数据来源于2020年中国人口密度分布图[10],降噪物密度指标的数据来源于中国-东盟1 km分辨率植被覆盖度数据集[11],生态不可分割度指标的数据来源于2020年中国土地利用图[12]。
1.3 蚁群算法
本研究将传统蚁群算法中的“往返时间”概念扩大至“成本”,在ArcGIS 10.7软件中的Python拓展模块实现蚁群算法,其步骤为:1)首先,进行路网处理,将道路以节点为界限划分路段,且对节点进行编号;2)之后,在Python拓展模块中编写程序,程序中对传统蚁群算法中的期望函数与信息素更新规则进行改进,以体现道路对生态环境的恶劣影响与改进经济成本代表指标。
基本蚁群算法涉及到2个过程。第一个过程是状态转移,蚁群算法中的状态转移概率函数由节点间距离与信息素浓度共同决定。i及j节点之间状态转移概率函数Pijm的计算方式如式(1)所示。
Pmij={ταij⋅ηβij∑j(ταij⋅ηβij),i,j∈list0,else (1) 式中:m为蚂蚁数量;α为信息启发因子,表示信息素浓度的重要性,取值为0~5;β为期望启发因子,表示节点之间成本的重要性,取值为0~5;τij为i、j节点之间的信息素浓度;ηij为从i节点到j节点的期望值。传统蚁群算法中期望函数ηij的计算方式如式(2)所示。
ηij=1lij (2) 第二个过程是信息素更新,(t+1)时刻i、j节点之间路段上信息素浓度τij(t+1)的计算方式如式(3)、式(4)所示。
τij(t+1)=(1−ρ)τij(t)+Δτij(t) (3) Δτij(t)=∑mk=1Δτkij(t) (4) 式中:ρ为信息素挥发系数;1-ρ为信息素残留系数;Δτij(t)为t时刻所有蚂蚁在节点i、j间留下的信息素浓度;Δtijk(t)为t时刻第k只蚂蚁在节点i、j间带来的信息素增量。
信息素增量的计算方式有3种:蚁周模型、蚁量模型、蚁密模型。本研究选择不容易陷入局部最优的蚁周模型为信息素更新规则。传统蚁群算法中的信息素更新规则如式(5)所示。
Δτkij(t)=Qlij (5) 式中:Q为信息素总量,取值范围为10~10 000;lij为i、j节点之间的道路长度。
1.4 客观权重赋值法
本研究利用 SPSS 软件实现 CRITIC 法与熵权 TOPSIS 法对综合成本指标的权重分配,其步骤为:1)建立综合成本评价指标体系;2)获取评价所需数据并建立道路数据集;3)以 CRITIC 法对环境成本指标下各子指标进行权重分配;4)以熵权 TOPSIS 法对综合成本指标下的时间成本与环境成本进行权重分配,环境成本权重与时间成本权重的比值即为新定义的环境干扰因子。
客观权重赋值法与以层次分析法等为代表的主管权重赋值法相比,只关注指标数据之间的差异,仅从数据中生成属性权重,而不需要从使用者中获取任何偏好信息[13],也可有效降低决策方法的复杂性与非直观性[14]。其中,CRITIC算法考虑了各指标自身的对比强度及指标间的冲突性,能够较全面的衡量各指标重要性,因而被作为一种相对完善赋权算法,被广泛使用。熵权法可用于分析对象之间存在较大差异的指标。它们均可用于整合社会影响评估和不同标准的确定。
1.5 基于CRITIC法与熵权TOPSIS法的综合成本计算
本研究利用客观权重赋值法中的CRITIC权重法与熵权TOPSIS 法建立道路综合成本评价体系,在体系中纳入道路交通对自然生态、人居环境的影响,并将该体系应用于所研究县级市路网中,以获得各路段的综合成本数值,为下一步计算得到综合成本最低的垃圾收运路径方案做好数据准备。
首先,考虑到数据的可达性与时效性,本研究取道路长度与限速之比为时间成本;环境成本由土地保护需求、影响人口规模、降噪物密度、生态不可分割度确定。
本研究使用时间成本与环境成本作为综合成本Cij的2大指标,其计算方式如式(6)所示。
cij=tij+γeij (6) 式中:tij为i、j节点之间道路的时间成本;γ为环境干扰系数;eij为i、j节点之间道路的环境成本。
时间成本tij的计算方式如式(7)所示。
cij=lij/vij (7) 式中:lij为i、j节点之间道路的长度,km;vij为i、j节点之间的车速,km∙h−1,由道路限速与车辆最高行驶速度确定。
环境成本eij的计算方式如式(8)所示。
eij=λ1·eij,1+λ2·eij,2+λ3·eij,3+λ4·eij,4 (8) 式中:λ1为土地退化态势的权重,0~1;eij,1为i、j节点之间道路穿行的土地退化态势;λ2为人口密度的权重,0~1;eij,2为i、j节点之间道路穿行地区的人口密度;λ3为植被覆盖度的权重,0~1;eij,3为i、j节点之间道路穿行地区的植被覆盖度;λ4为生态抗扰度的权重,0~1;eij,4为i、j节点之间道路穿行地区的生态抗扰度。
利用CRITIC法赋予环境成本中各指标权重,并利用熵权法计算环境干扰因子。时间成本由道路长度与道路限速之比得到。之后,编辑路网数据集,添加“时间”字段,通过字段计算器算的每段道路通过所需花费的时间。
2. 结果与分析
2.1 生态干扰程度
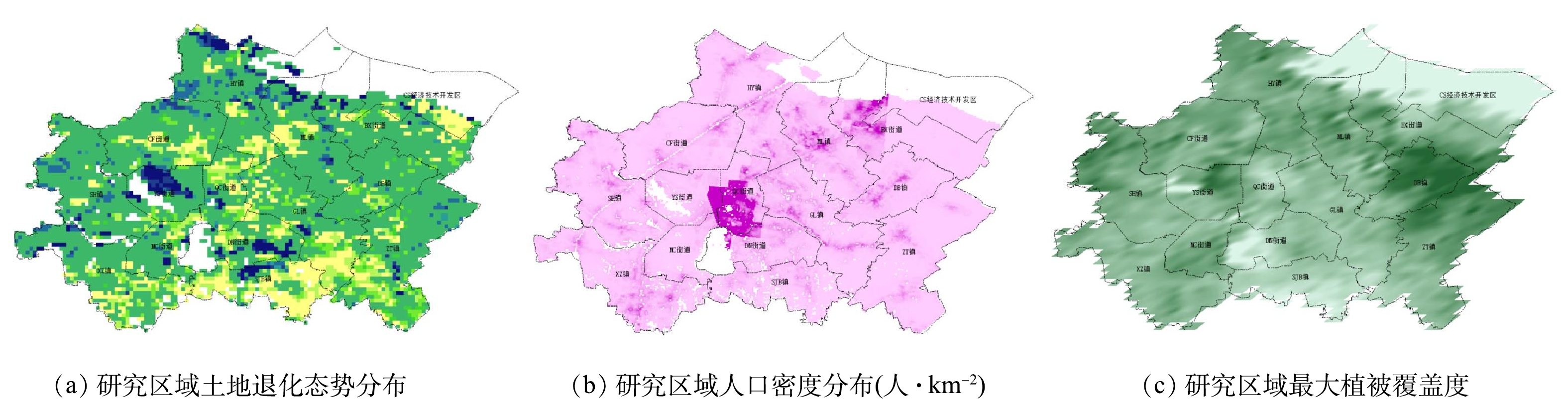
垃圾运输对运输区域的生态干扰程度主要由土地保护需求、影响人口规模以及降噪物密度决定。本研究利用土地退化态势来确定土地保护需求。土地退化态势数据集中,将全球的土地退化态势分为2级评价系统。在第1级,将土地退化态势评价划分为3种类型:退化类型、改善类型和无变化类型。第2级,将土地退化态势评价划分为9种类型。下载土地退化态势数据集后,在ArcGIS软件中打开,并根据研究区域行政区划线要素矢量数据图对其裁剪,得到如图2(a)所示的研究区域土地退化态势分布栅格图,图中颜色越浅表示土地退化越严重。
影响人口规模由人口密度分布确定。将人口密度分布栅格数据经过裁剪与符号化后标注于研究区域地图,通过识别功能得到各垃圾中转站所处位置的人口密度。研究区域人口密度栅格图像如图2(b)所示。图中颜色越深,表明人口密度越大。
降噪物密度由植被覆盖度确定。植被覆盖度数据的处理方式同土地退化态势分布图,结果如图2(c)所示。图中颜色越深,表示植被覆盖度越大。
2.2 生态不可分割度
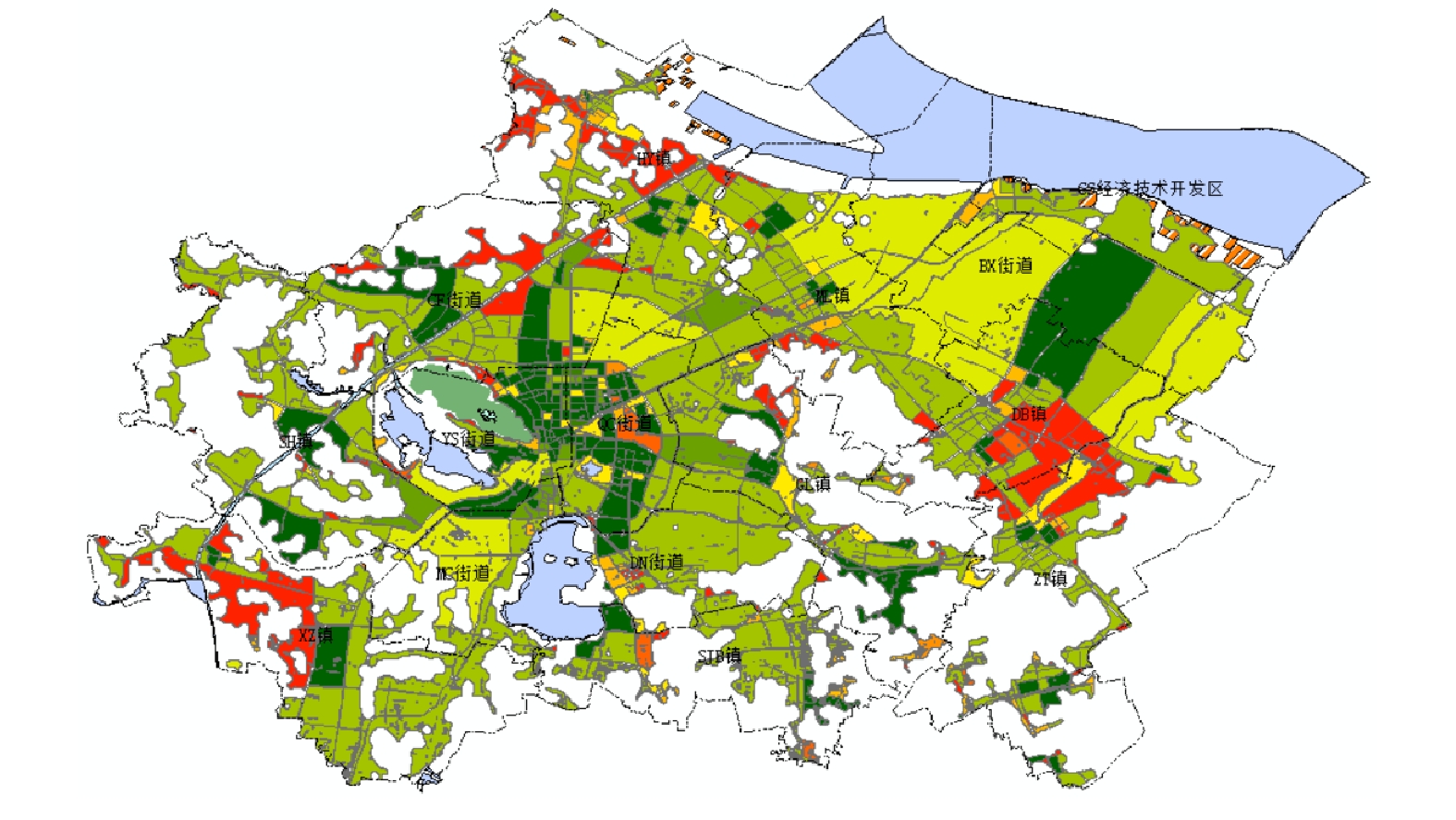
在环境成本保护的各指标中,生态不可分割度为本研究根据生物丰度指数含义进行改进得到的指标,旨在评价道路交通沿线周边生态系统对道路切割的抵抗力,以减少堵路交通对沿线周边造成的不可逆性深远影响。生态不可分割度越高,往往当地生态系统所含的食物链就越复杂,则道路交通对当地生态环境切割与生物栖息地破碎化的负面影响就越深。根据我国生态环境部颁布的《生态环境状况评价技术规范(HJ 192-2015)》[15]的标准,定义生态抗扰度的打分方式如表1所示。利用空间地理数据云的2020年中国土地利用图矢量数据计算生态不可分割度,经过裁剪,其结果如图3所示。图中颜色越接近红色,城市化程度越高,生态不可分割度得分越低。
表 1 土地利用类型与生态不可分割度得分的映射关系Table 1. Mapping relationship between land use type and ecological indivisibility score土地利用类型 基础分数 结构类型 修正系数 土地利用类型 基础分数 结构类型 修正系数 林地 100 有林地 1 耕地 31 水田 1 灌木林地 0.75 旱地 0.67 疏林地和其他林地 0.5 建筑用地 11 城镇建设用地 0.75 草地 60 高覆盖度草地 1 农村居民地 1 中覆盖度草地 0.75 其他建设用地 0.75 低覆盖度草地 0.5 未利用地 3 沙地 0.67 水域湿地 80 河流 0.5 盐碱地 1 湖泊(库) 0.75 裸土地 1 滩涂湿地 1 裸岩石砾 0.67 2.3 多元数据的整合
在环境成本的所有指标中,土地利用类型为矢量数据,其匹配方式为,选中路网文件,选择“连接和关联”中的“连接”,并基于空间位置来连接土地利用类型图层。其余的指标均为栅格数据,只需要在已有的路网矢量数据添加上相对应的栅格数据值即可。至此,研究区域各路段已被赋予环境成本数值。之后,在SPSSAU平台上利用CRITIC权重法计算环境成本中各指标权重。计算结果如表2所示。据此可得到各路段取值为0~1的环境成本数值。
表 2 CRITIC法计算结果Table 2. Calculation results of CRITIC method考察项目 指标变异性 指标冲突性 信息量 权重系数 土地退化态势 0.239 2.604 0.622 22.87% 人口密度 0.069 2.802 0.195 7.16% 植被覆盖度 0.178 2.833 0.505 18.56% 生态不可分割度 0.446 3.133 1.398 51.41% 对于环境干扰因子的取值,首先使用熵权法对时间成本与环境成本的权重进行赋值,其次取环境干扰因子的值为环境成本与时间成本权重的比值。在SPSSAU平台上进行熵权法计算后,结果如表3所示:
表 3 熵权法计算结果Table 3. Calculation results of Entropy Weight TOPSIS method考察项目 信息熵值e 信息效用值 权重系数 时间成本 0.817 7 0.182 3 89.96% 环境成本 0.979 6 0.020 4 10.04% 环境干扰因子取值为0.1116。据此计算研究区域路网中所有路段的综合成本,之后在ArcGIS里的路段属性表中添加综合成本字段,完善路网数据集。
2.4 传统蚁群算法的实现
为考察综合成本对垃圾收运路径规划的影响,本研究先基于传统蚁群算法进行垃圾收运路径规划设计,然后与以改进蚁群算法为原理的规划路径作对比分析。传统蚁群算法中将“距离”作为经济成本的代替数据,以路径最短作为计算目标。
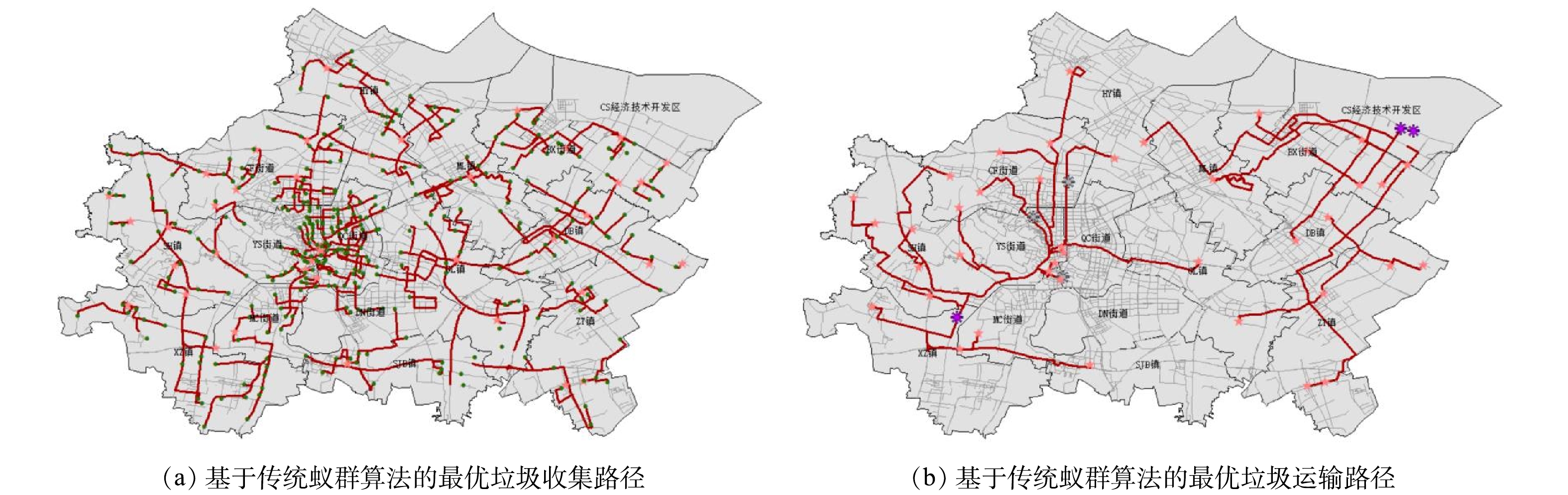
本研究中蚁群算法的实现依托于ArcGIS10.7 软件中的Python拓展模块。本研究区域的垃圾收集点与垃圾中转点数较多,所以用PyPy代替Python中的解释器CPython,将源代码直接转换为机器汇编语言,以大幅提升程序运行效率。程序运行后,输出最佳路径的节点编号。将节点选择结果标记至ArcGIS 10.7中的路网图上,得到基于传统蚁群算法的综合成本最低的收集路径、运输路径。结果如图4(a)、(b)所示。
2.5 改进蚁群算法的实现
为了修正传统蚁群算法对计算目标设定与指标选取的局限性,本研究以改进传统蚁群算法中期望函数定义与信息素浓度更新规则的方式,在蚁群算法计算最优路径时引入时间成本与环境成本,以改正原路径计算方法用“距离”代表经济成本、忽略环境影响的缺陷。其中,改进蚁群算法中期望函数的计算方式如式(9)所示。
ηij=1cij (9) 式中:cij为i、j节点之间的综合成本。
本研究选择不容易陷入局部最优的蚁周模型为信息素更新规则,并结合将“成本”代替“路径长度”的理念,规定信息素更新规则为信息素总量与成本之比。其计算方式如式(10)所示。
Δτkij(t)={QCk,蚂蚁k经过路径(i,j)0,其他 (10) 式中:Q为信息素总量;Ck为蚂蚁k在本次遍历中所走路径小号的综合成本。
综合成本Ck的计算方式如式(11)所示。
Ck=Tk+γEk (11) 式中:Tk为蚂蚁k在本次遍历中所走路径消耗的时间成本;Ek为蚂蚁k在本次遍历中所走路径消耗的环境成本。
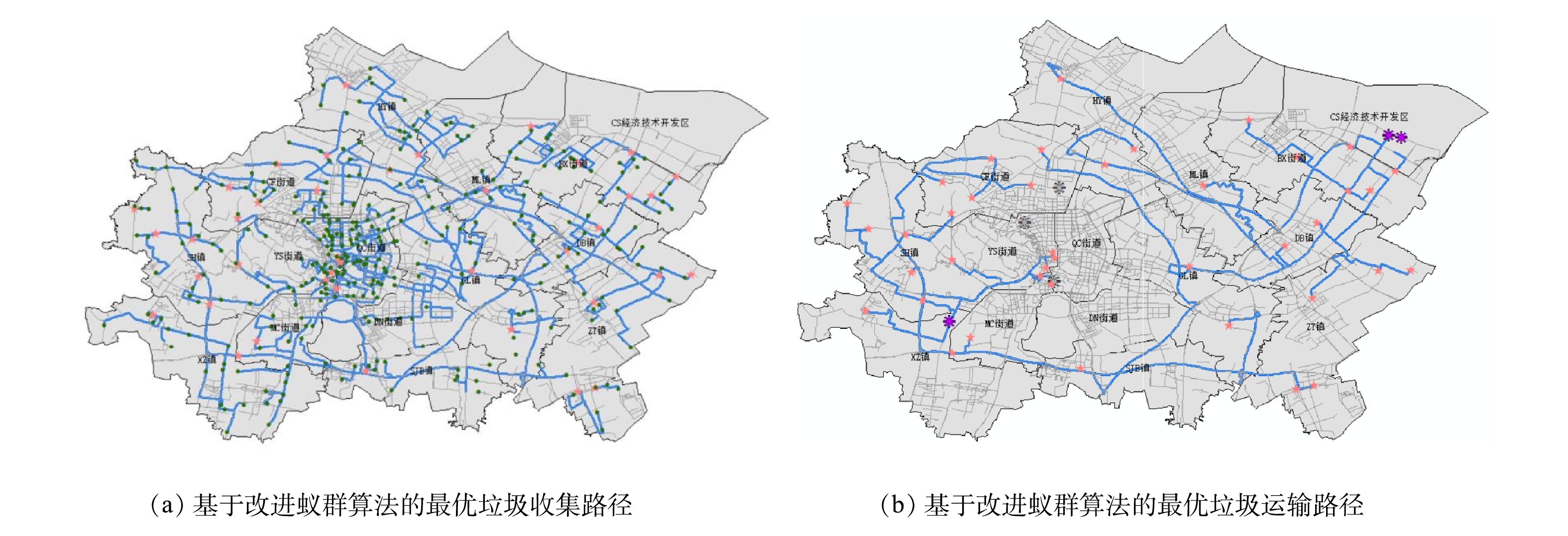
实现改进蚁群算法需要基于路段的综合成本属性,所以需要构建新的网络数据集。与传统蚁群算法相比,改进蚁群算法需要在新的数据集指定属性时添加综合成本,并在配置网络行驶方向时设置阻抗为综合成本,其余步骤与之前相同。程序运行后,根据运算所得到的节点选择相应结果,标记路网地图,得到基于改进蚁群算法的综合成本最低的收集路径与运输路径,结果如图5(a)、(b)所示。从图可以看出,基于改进蚁群算法得到的垃圾收集路径与垃圾运输路径均与基于传统蚁群算法计算得到的结果有明显不同。
2.6 对比与分析
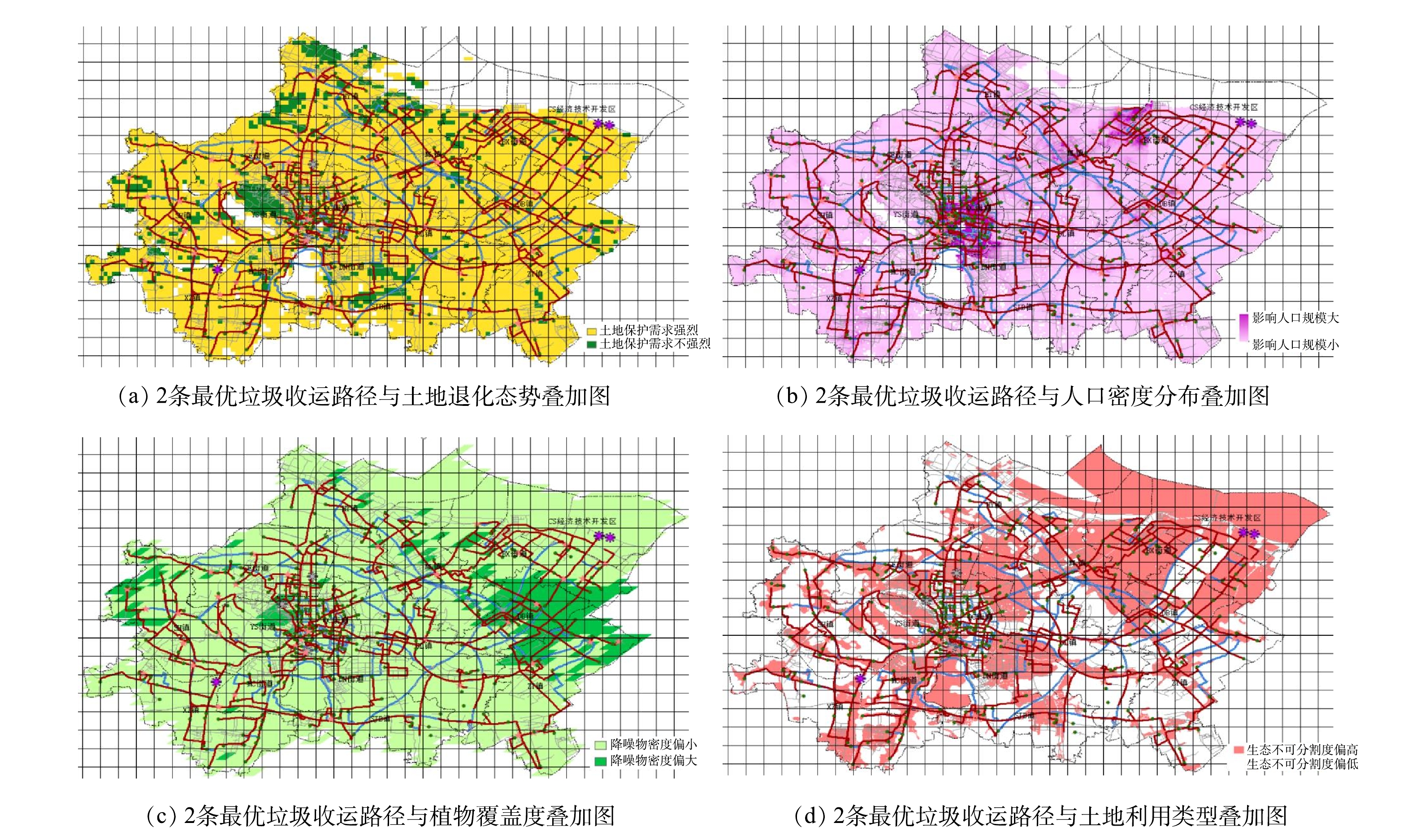
为进一步分析利用 CRITIC 法与熵权 TOPSIS法构建的路径综合成本评价体系对垃圾收运路径规划的影响,本节分别以环境成本中纳入的4项环境成本指标数据图为底图,用分辨率为1 km×1 km 的表格划分研究区域,定义被规划路径穿行的敏感区域(后面将分别定义)所占格子个数与规划路径穿行格子总数之比为规划路径对敏感地区的穿行率。计算基于2种蚁群算法算出的垃圾收运路径规划结果的穿行率并进行对比,讨论考虑环境成本后的最优垃圾收运路径与仅考虑经济成本的结果有何不同。如图4和图5所示,红色路径均为基于传统蚁群算法求得的最优垃圾收运路径,蓝色路径均为基于改良蚁群算法求得的最优垃圾收运路径。
将基于传统蚁群算法与改进蚁群算法得到的最优垃圾收集路径、运输路径均标记在土地退化态势图中,结果如图6(a)所示。底图的颜色越浅,表示土地退化越严重。定义土地退化态势为负数的区域为土地保护需求强烈区域(敏感区域),则分析图6(a)可知,红线对土地保护需求强烈区域的穿行率为81%,蓝线对土地保护需求强烈区域的穿行率为48%,蓝线较红线而言土地保护需求强烈区域穿行率减少了41%。可见,红线比蓝线更集中于土地退化严重的区域,而蓝线多分布于土地质量正在改善或不退化的区域。将土地保护需求纳入垃圾收运路径规划后,可有效缓解垃圾收运交通对土地退化的进一步恶劣影响,从而促进了退化土地恢复与土地质量改善。
将基于传统蚁群算法与改进蚁群算法得到的最优垃圾收集路径、运输路径均标记在人口密度分布图中,结果如图6(b)所示。底图的颜色越深,表示人口密度越大。定义人口密度大于中位数 311 人∙km−2的区域为影响人口规模偏大区域(敏感区域)。分析图6(b)可知,红线对影响人口规模偏大区域的穿行率为2%,蓝线对影响人口规模偏大区域的穿行率为18%。与红线相比,蓝线影响人口规模偏大区域穿行率减少了44%。可见,红色线条比蓝色线条更集中于人口密集区域,而蓝色线条多分布于人口密度较小的地方,整体布局也更加均匀。人口规模大的区域往往交通繁忙,将影响人口规模纳入垃圾收运路径规划后,不仅能绕开人口密度大的居住地从而改善人居环境,还能有效缓解拥堵路段,从而缩减垃圾收运时间、提高垃圾收运效率、减少车辆运行造成的环境污染。
将基于传统蚁群算法与改进蚁群算法得到的最优垃圾收集路径、运输路径均标记在植物覆盖度图中,结果如图6(c)所示。底图的颜色越深,表示植物覆盖度越大,对车辆噪音的削减能力越强。定义植物覆盖度小于中位数192的区域为降噪物密度偏小区域(敏感区域)。分析图6(c)可知,红线对降噪物密度偏小区域的穿行率为76%,蓝线对降噪物密度偏小区域的穿行率为54%,蓝线较红线而言降噪物密度偏小区域穿行率减少了9%。可见,红线比蓝线更集中于难以被植物削减噪音的区域,而蓝线多分布于容易被植物削减噪音的区域。将降噪物密度指标纳入垃圾收运路径规划后,可将垃圾收运路径更多转移至植物密度高的地方,使车辆通行产生的噪音得到更大程度的削减,从而减轻了垃圾收运交通噪音对人类的影响,提高了人居环境质量。
将基于传统蚁群算法与改进蚁群算法得到的最优垃圾收集路径、运输路径均标记在土地利用类型图中,结果如图6(d)所示。图中颜色越接近红色,城市化程度越高,生态不可分割度得分越低。定义生态不可分割度大于中位数40的区域为生态不可分割度偏大区域(敏感区域)。分析图6(d)可知,红线对生态不可分割度偏大区域的穿行率为83%,蓝线对生态不可分割度偏大区域的穿行率为49%,蓝线较红线而言生态不可分割度偏大区域穿行率减少了41%。可见,红线比蓝线更集中于不应被人为分割的区域,而蓝线多分布于已进行过人为建设的区域,即红线比蓝线更集中于生态不可分割度高(城市化程度高)的区域。将生态不可分割度纳入垃圾收运路径规划后,可有效减轻垃圾收运交通对周边生态环境的切割程度,减少了人类活动对自然度高的区域的进一步干扰,从而在一定程度上保护了物种多样性与生态稳定性。
3. 结论
1)以“耗时”作为经济成本的衡量指标,将限速情况等路况因素考虑在内,可以充分体现包括路径长度在内的耗油量、人力成本等额外经济成本,从而更利于道路交通经济成本的控制。
2)基于人口密度分布等数据,将道路交通对周边人群健康、生态环境质量的影响纳入对道路交通的综合成本评价当中,对蚁群算法进行了因地制宜的改良,将规划路径对土地保护需求强烈区域、影响人口规模偏大区域、降噪物密度偏小区域、生态不可分割度偏大区域的穿行率分别降低了41%、44%、29%、41%。
-
表 1 2种板型几何参数
Table 1. Geometric parameters of two plate types
板型 线间距A/mm 板间距B/mm 通道长度C/mm 极板长度D/mm 空腔厚度E/mm 线径r/mm 孔径H/mm 孔间距P/mm 平板 240 400 2 000 1 440 50 1 — — 多孔板 240 400 2 000 1 440 50 1 30 50 表 2 边界条件设置
Table 2. Boundary condition setting
位置 流场 颗粒 电场 空间电荷 入口 Ux=U0 Ux=U0 ∂ϕ∂n=0 ∂ρion∂n=0 出口 压力出口 冻结 ∂ϕ∂n=0 ∂ρion∂n=0 收尘极 无滑移 冻结 φ=0 ∂ρion∂n=0 放电极 无滑移 反弹 φ= φ0 Peek law 圆孔边界 无滑移 冻结 φ=0 ∂ρion∂n=0 -
[1] 安连锁, 王金平, 郦建国, 等. 中国燃煤电厂电除尘技术发展及应用综述[J]. 中国电力, 2018, 51(4): 115-123. [2] WHITE H J. Industrial electrostatic precipitation[M]. MA: Addison Wesley, 1963. [3] ZHAO H, CHEN K Y, LIU Z, et al. Coordinated control of PM2.5 and O3 is urgently needed in China after implementation of the “Air pollution prevention and control action plan”[J]. Chemosphere, 2021, 270: 129441-129441. doi: 10.1016/j.chemosphere.2020.129441 [4] 刘艳梅, 闫静, 徐文帅, 等. 超低排放改造后燃煤电厂常规大气污染物排放特征[J]. 环境科学学报, 2020, 40(6): 1967-1975. [5] 郝吉明, 段雷, 易红宏, 等. 燃烧源可吸入颗粒物的物理化学特征[M]. 科学出版社, 2008. [6] CHOI H Y, Park Y G, Ha M Y, et al. Numerical simulation of the wavy collecting plate effects on the performance of an electrostatic precipitator[J]. Powder Technology, 2021, 382: 232-243. doi: 10.1016/j.powtec.2020.12.070 [7] GAO M, ZHU Y, YAO X, et al. Dust removal performance of two-stage electrostatic precipitators and its influencing factors[J]. Powder Technology, 2019, 348: 13-23. doi: 10.1016/j.powtec.2019.03.016 [8] DONG M, ZHOU F, SHANG Y, et al. Numerical study on electrohydrodynamic flow and fine-particle collection efficiency in a spike electrode-plate electrostatic precipitator[J]. Powder Technology, 2019, 351: 71-83. doi: 10.1016/j.powtec.2019.03.046 [9] ZHU Y, GAO M, CHEN M, et al. Numerical simulation of capture process of fine particles in electrostatic precipitators under consideration of electrohydrodynamics flow[J]. Powder Technology, 2019, 354: 653-675. doi: 10.1016/j.powtec.2019.06.038 [10] KALLIO G A, STCOK D E. Interaction of electrostatic and fluid dynamic fields in wire-plate electrostatic precipitators[J]. Journal of Fluid Mechanics, 1992, 240(1): 133-166. [11] LIANG W J. The characteristics of ionic wind and its effect on electrostatic precipitator[J]. Quality Assurance Journal, 1994, 5(4): 241-245. [12] HANS J S, STEFFEN S, HANS B. On the modelling of the Electro-Hydrodynamic flow field in electrostatic precipitators[J]. Flow, Turbulence and Combustion, 2002, 68(1): 63-89. doi: 10.1023/A:1015666116174 [13] CHUN Y N, ChANG J S, BEREZIN A A, et al. Numerical modeling of near corona wire electrohydrodynamic flow in a wire-plate electrostatic precipitator[J]. IEEE Trans. Dielect. Elect. Insul, 2007, 14(1): 119-124. doi: 10.1109/TDEI.2007.302879 [14] YAMAMOTO T. Effects of turbulence and electrohydrodynamics on the performance of electrostatic precipitators[J]. Journal of Electrostatics, 1989, 22(1): 11-22. doi: 10.1016/0304-3886(89)90106-X [15] LONG Z W, YAO Q. Evaluation of various particle charging models for simulating particle dynamics in electrostatic precipitators[J]. Journal of Aerosol Science, 2010, 41(7): 702-718. doi: 10.1016/j.jaerosci.2010.04.005 [16] WAWLESS P A. Particle charging bounds, symmetry relations, and an analytic charging rate model for the continuum regime[J]. Journal of Aerosol Science, 1996, 27(2): 191-215. doi: 10.1016/0021-8502(95)00541-2 [17] 周栋梁, 李水清, 靳星, 等. 电场、流场耦合作用下脱除细颗粒物的实验和数值模拟[J]. 中国电机工程学报, 2016, 36(2): 453-458. [18] OUNIS H, AHMADI G, MCLAUGHLIN J B, et al. Brownian diffusion of submicrometer particles in the viscouse sublayer[J]. Journal of Colloid and Interface Science, 1991, 143: 66-277. [19] FRIEDLANSER S K, WILLIAM H M. Smoke, Dust and Haze: Fundamentals of Aerosol Behavior[J]. Phys. Today, 1977, 30(9): 58-58. doi: 10.1063/1.3037714 [20] KAPTZOV N A, Elektricheskie invlentiia v gazakh i vakuumme[M]. OGIZ, Moscow, 1947. [21] PEEK F W, Dielectric phenomena in high voltage engineering[M]. 3rd ed McGraw-Hill, New York, 1929. [22] PENNEY G W, MATICK R E. Potentials in D-C corona fields[J]. American Institute of Electrical Engineers, Part I:Communication and Electronics, Transactions of the, 1960, 79(2): 91-99. [23] LAWLESS P A, SPARKS L E. A mathematical model for calculating effects of back corona in wire‐duct electrostatic precipitators[J]. Journal of Applied Physics, 1980, 51(1): 242-256. doi: 10.1063/1.327416 [24] 沈欣军. 电除尘器内细颗粒物的运动规律及其除尘效率研究[D]. 浙江大学, 2015. [25] 沈欣军, 郑钦臻, 宁致远, 等. 燃煤电厂电除尘PM10和PM2.5的排放控制Ⅳ: 采用二维PIV除尘[J]. 科技导报, 2014(33): 43-50. doi: 10.3981/j.issn.1000-7857.2014.33.005 [26] AHMED K. Computation and measurement of corona current density and V-I characteristics in wires-to-plates electrostatic precipitator[J]. Journal of Electrostatics, 2016, 81: 1-8. doi: 10.1016/j.elstat.2016.02.005 [27] 张建平, 陈思艺, 王帅, 等. 扩散荷电对两种ESP除尘性能影响的对比分析[J]. 环境工程, 2019, 37(8): 143-147. [28] 高梦翔, 姚鑫, 朱勇, 等. 双区静电除尘器的数值模拟研究[J]. 中国环境科学, 2018, 38(10): 3698-3703. doi: 10.3969/j.issn.1000-6923.2018.10.012 -






 下载:
下载: