太湖富营养化问题突出。多年来，大多研究集中在蓝藻水华问题形势严峻的太湖西部和北部区域^[9]，而对太湖东部湖区的研究相对较少。根据江苏省环境监测中心长期水质及卫星遥感监测结果，2016年前，太湖东部湖区水质较好，TP较低，未曾出现蓝藻水华现象；而2016年以后，太湖东部湖区开始出现蓝藻水华，同时TP逐渐升高。一是由于入湖的磷污染物大幅增加，并通过湖体水动力变化，逐年从西向东迁移^[10]；二是由于东太湖水生植被的大量减少，沉水植物对磷元素的吸收相应减少，增加了风浪对底泥扰动导致的内源性营养盐的释放^[11]。此外，TP变化还与风向、风速等因素密切相关^[12]。2019年个别月份，太湖东部湖区金墅港和渔洋山水源地的TP甚至超过地表水环境质量标准(GB 3838-2002)集中式生活饮用水源地二级保护区Ⅲ类标准值，直接威胁饮用水水源地水质安全。

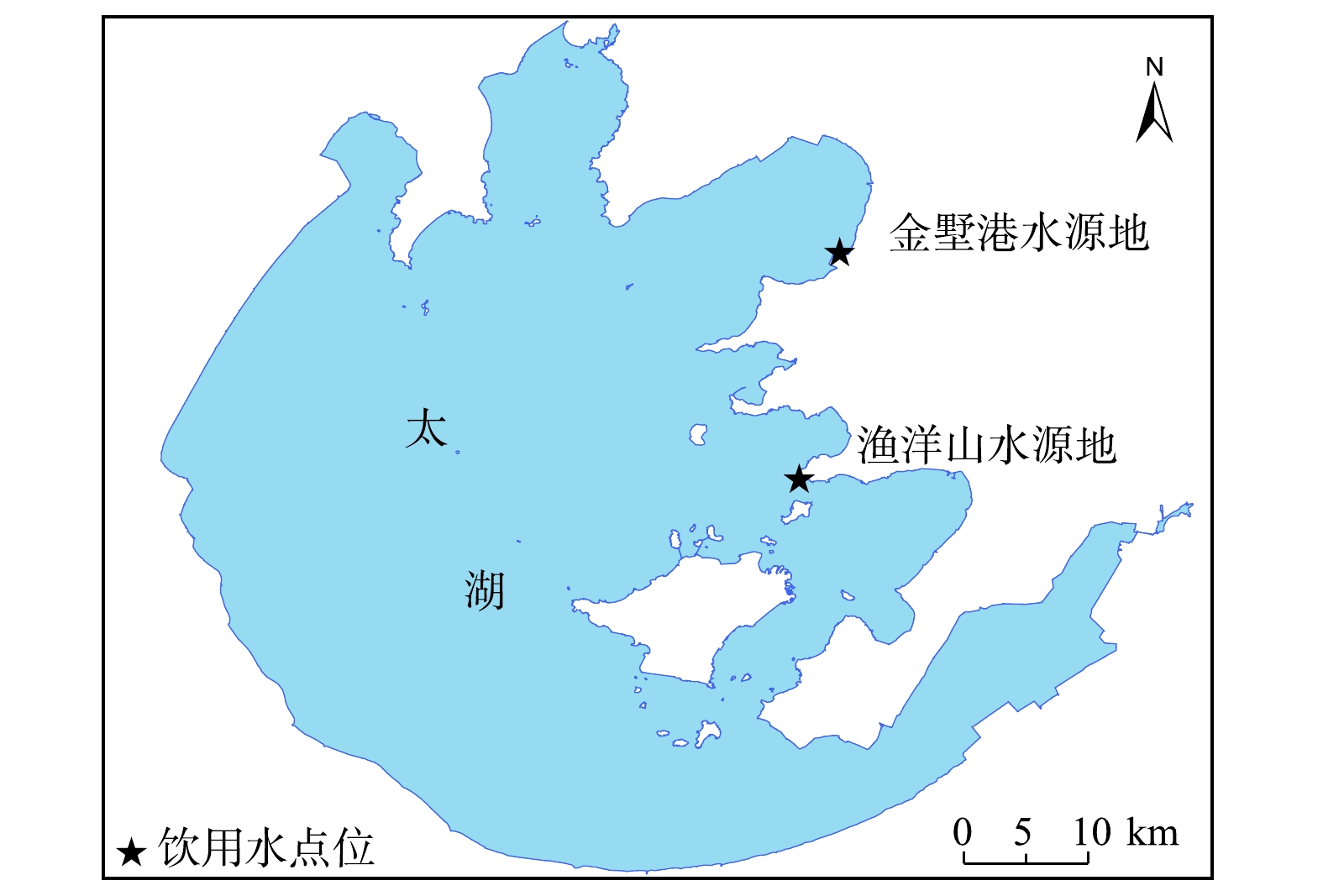
太湖东部湖区金墅港、渔洋山水源地(位置如图1所示)的TP自动监测数据频次为每2 h一次，较高的数据量可实现TP的有效监测。目前，这2处水源地的TP自动监测仪器是日本岛津TNP4110，测定原理是采用碱性过硫酸钾消解-紫外分光光度法分析水样中的TP，仪器稳定性好，分析方法符合国家环境保护行业标准HJ 103-2003的要求。然而，若出现较大风浪导致水体浑浊，以及水体中出现过多蓝藻颗粒等情况时，会干扰TP消解和比色过程，此时TP的测定浓度并不能准确反映TP的实际情况^[13]。本研究选用金墅港、渔洋山水源地2016年1月—2020年4月的TP自动监测数据，与实验室监测数据进行比对分析。实验室监测数据频次为每月一次，方式为手工采样。采样点位于自动监测站取水口，样品的采集、运输、保存均执行地表水采样技术规范(HJ 91-2002、HJ 493-2009)。实验室分析采用钼酸铵分光光度法(GB 11893-1989)。实验室监测数据能准确反映水源地TP，可作为TP自动监测数据的真值。比对分析时，自动监测选用在采样时间上与实验室手工采样时间最为临近的一组数据，时间差为0~59 min。

极限学习机(ELM)是一个单隐层的神经网络，是在Moore-Penrose矩阵理论基础上提出的快速学习算法^[14-15]。相较传统的神经网络具有训练速度快、参数选择简单、不易陷入局部最优等特点，可运用于水质评价和水质预测等方面。已有研究^[16]表明，ELM 网络模型已在多输入、多输出的水质预测中取得了较好的效果。

根据极限学习机理论^[4-5]，对于一个有L个节点的单隐层神经网络可表示为式(1)。

式中：$ g\left(x\right) $为激活函数， $ {W}_{i}={\left[{W}_{i1},{W}_{i2},\cdots ,{W}_{in}\right]}^{\mathrm{T}} $为连接第i个隐层节点的输入权值；$ {b}_{i} $为第i个隐层节点的偏置；$\; {\beta }_{i}={\left[{\beta }_{i1},{\beta }_{i2},\cdots ,{\beta }_{im}\right]}^{\mathrm{T}} $为第i个隐层节点的输出权值。令$ H=g\left({W}_{i} \cdot {X}_{j}+{b}_{i}\right) $，则式(1)可换算为式(2)。

式中：$H({W}_{1},{W}_{2},\cdots ,{W}_{L},{b}_{1},{b}_{2},\cdots ,{b}_{L},{x}_{1},{x}_{2},\cdots ,{x}_{N})=\left[\!\!{array}{ccc}g\left({W}_{1} \cdot {X}_{1}+{b}_{1}\right)& \cdots & g\left({W}_{L} \cdot {X}_{1}+{b}_{L}\right)\\ \vdots & \ddots & \vdots \\ g\left({W}_{1} \cdot {X}_{N}+{b}_{1}\right)& \cdots & g\left({W}_{L} \cdot {X}_{N}+{b}_{L}\right){array}\!\!\right]$；$ \beta ={\left[\!\!{array}{c}{\beta }_{1}^{\mathrm{T}}\\ \vdots \\ {\beta }_{L}^{\mathrm{T}}{array}\!\!\right]}_{L \times M}$；$T={\left[\!\!{array}{c}{t}_{1}^{\mathrm{T}}\\ \vdots \\ {t}_{N}^{\mathrm{T}}{array}\!\!\right]}_{N \times M} $。

为达到训练效果，需要得到$ {W}_{i} $、$ {\beta }_{i} $、$ {b}_{i} $使式(2)无限接近于最小化，得到式(3)。

由此得到等价的最小化损失函数，见式(4)。

在ELM算法中, 一旦输入权重$ {W}_{i} $及隐层的偏置$ {\beta }_{i} $被随机确定，隐层的输出矩阵$ H $就被确定。训练单隐层神经网络可转化为求解一个线性系统$ H\beta =T $，并且输出权重$ \beta $的范数最小且唯一，计算公式见式(5)。

式中：$ {H}^{-1} $是矩阵$ H $的Moore-Penrose广义逆。

根据ELM原理，隐层节点数越多，训练误差会越小。当隐层节点数等于样本数时，训练误差会趋于0；但会由此造成算法隐层节点的冗余，且一些隐含层节点并无意义^[16-17]，故有学者在水质评价时通过粒子群算法来优化极限学习机的输入权值和隐含层偏置^[6]。然而，粒子群算法对离散的优化问题处理不佳，容易产生早熟收敛。本研究提出可选择极限学习机隐层节点的改进极限学习机模型(IELM，Improved ELM)，采用多次试验取平均值的方法确定隐层节点数。多次试验求平均可减少随机产生的权值和阈值对模型稳定性的干扰，并增强学习机的稳定性^[18-19]。通过试触法对每个节点数所建立的模型进行测试，分析测试误差的变化趋势，以此来确定合适的隐层节点数，可大大提升模型的预测精度，并有效降低随机值的产生对模型的干扰。

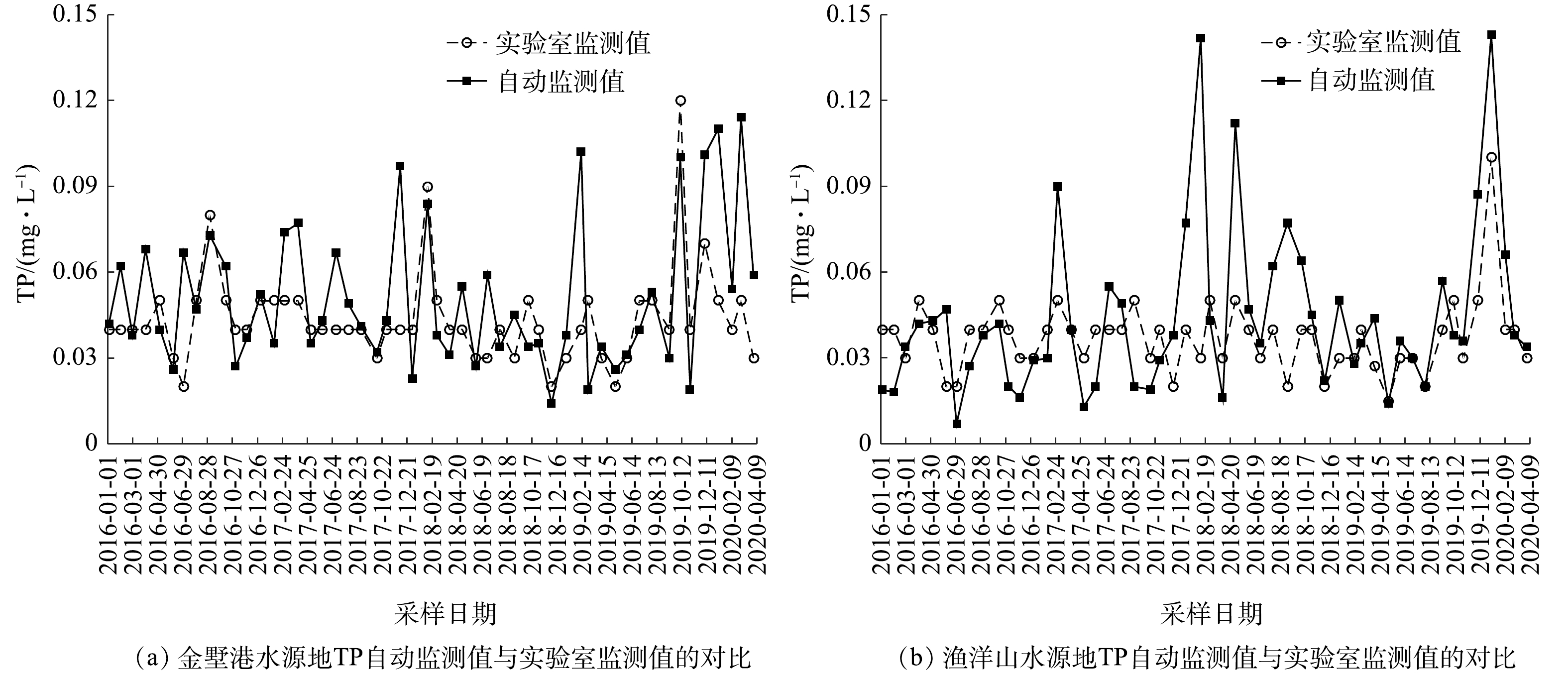
图2为2016年以来金墅港水源地和渔洋山水源地的TP自动监测和实验室监测值的对比图。由图2可见，TP自动监测值和实验室监测值相差值为−0.05~0.112 mg·L⁻¹，计算差值绝对值的平均值为0.017 mg·L⁻¹，相对于湖库型TP标准为Ⅱ类(0.01~0.025 mg·L⁻¹)；而最大值0.112 mg·L⁻¹，相对于湖库型TP浓度标准为Ⅴ类(0.1~0.2 mg·L⁻¹)。自动站每隔一段时间会将自动监测值与实测值进行人工比对，以确定自动站是否正常运行。根据《江苏省水质自动监测质量管理暂行规定(苏环监〔2012〕6号)》，将自动值和手工值之差与手工值的比值定为比对误差。比对误差在±30%以内，TP自动监测数据才能有效反应实际情况。由此计算得到TP自动监测数据的合格率仅为52.9%。

造成数据偏差较大的原因有如下几点。1)悬浮颗粒物是氮磷等营养元素在水中迁移转化的重要载体^[20]，同时也是微生物附着生长的重要载体^[11]，风浪等其他因素搅动底泥致使浊度增大，水中悬浮颗粒物增多，故实测数据偏大。2)悬浮物和蓝绿藻携带的TP经过消解转换为可检测的无机磷导致检测值较水体实际值高，另外蓝绿藻色度会干扰TP显色反应、浑浊的水质会干扰比色透光性亦会导致检测值和实际值产生偏差。3)对于实验室TP分析。根据《国家地表水环境质量监测网监测任务作业指导书(试行)(环办监测函〔2017〕249)》，TP人工采样静置及虹吸方式有利于粒径较大的颗粒物沉淀，可在一定程度上降低浊度对测定的干扰^{[3, 21]}。在对太湖进行的实际采样过程中，若水样藻类较多，会采用63 μm筛过滤掉部分藻，并在分析时采用浊度及色度补偿以消除实验室的比色干扰，以进一步降低对TP测定结果的影响。样品从采样、运输，到实验分析、数据报出都有完整的全过程质量控制，以确保人工监测数据准确性更高。

选取金墅港和渔洋山水源地水质自动监测站2016年1月—2020年4月的pH、溶解氧(DO)、浊度(Turb)、高锰酸盐指数(COD_Mn)、氨氮(${\rm{NH}}_4^ + $-N)、叶绿素质量浓度(Chl-a)、蓝绿藻密度(藻密度)等指标与TP进行相关性分析，自动监测频率为每2 h一次。结果表明：Turb与TP的相关性较高，相关系数为0.442；其次为藻密度，与TP的相关系数为0.207；相关性最小的为pH，与TP的相关系数为−0.015。各指标与TP的相关性分析结果见表1。

7个指标中，Chl-a、藻密度与TP的相关性较弱，分别为0.123、0.207。然而，也有学者发现太湖水质中的Chl-a、藻密度和TP呈显著正相关关系^{[11, 22-23]}；对与TP相关系数较大的Turb、藻密度和Chl-a等3项指标进行自相关分析发现，Turb与藻密度的相关性为0.139，具有一定相关性。以上结果的主要原因为颗粒态藻类会导致水体浊度增加，藻密度对水体色度会干扰显色反应，影响测定结果。其余指标之间相关系数均小于0.1，无相关性。

根据TP的影响因素分析，将TP自动监测值及对其影响较大的Turb、藻密度和Chl-a等指标数据作为模型的输入数据集，TP的实验室监测值作为模型测试数据集，构建ELM模型。

选取2个水源地2016年1月—2019年10月共92组数据为模型训练数据集，即训练样本数N=92；选取2个水源地2019年11月—2020年4月共12组数据作为模型测试数据集。为避免指标单位不统一对模型的影响，将Turb、藻密度和Chl-a进行归一化处理。正则化后的数据与TP自动监测值组合成数据输入集。

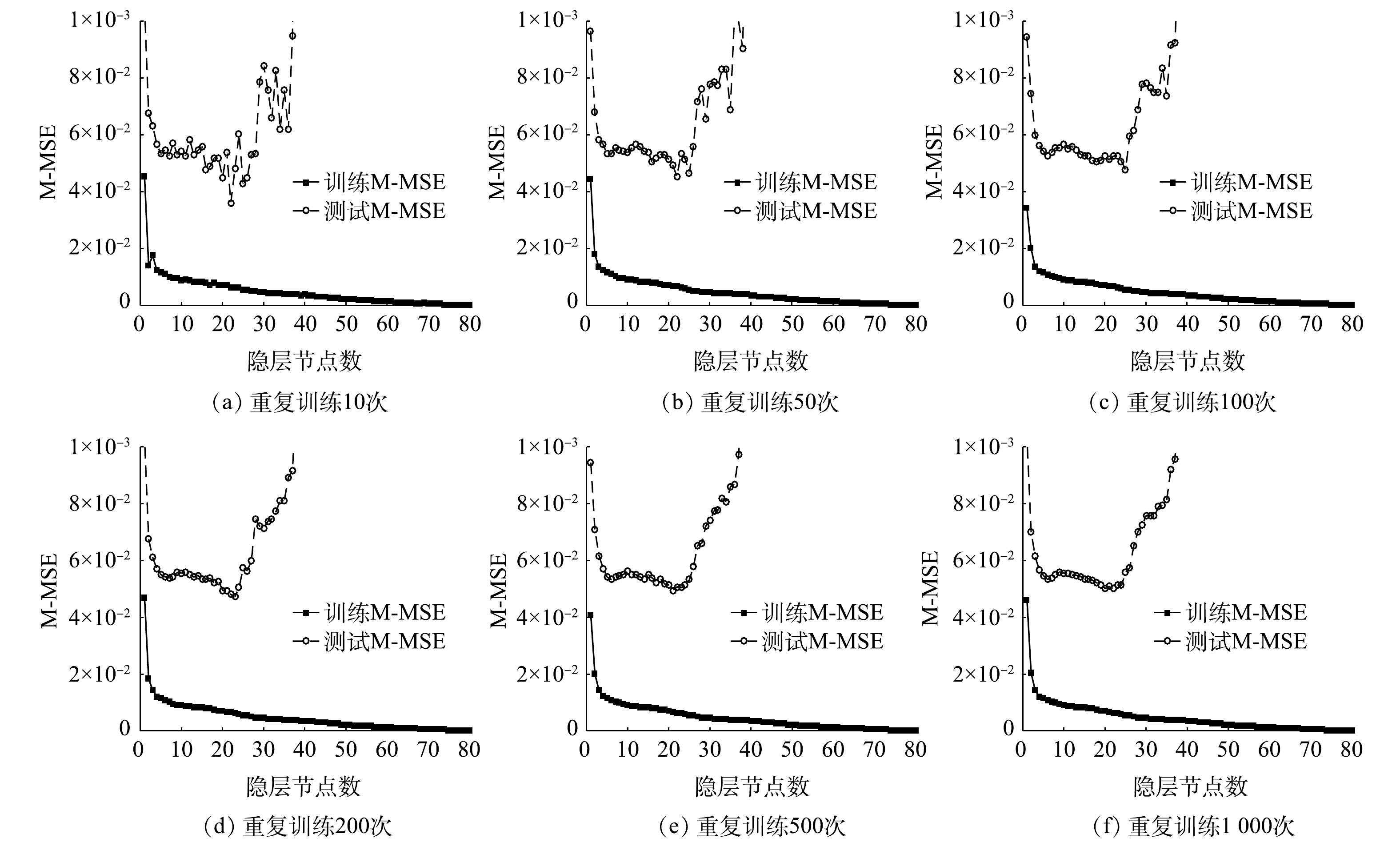
将92组训练样本数据单独分为训练样本和测试样本：前80组数据作为训练样本；后12组数据作为测试样本。以1~80作为隐层节点的个数，分别进行10次、50次、100次、200次、500次和1 000次的训练，分析不同训练次数与隐层节点数的平均均方误差(mean-mse，M-MSE)的变化规律，结果如图3所示。

由图3可见，重复训练10、50和100次的M-MSE随隐层节点数增加的变化趋势不稳定，说明训练次数较少不能很好地降低随机值干扰。训练200次以上，随机值干扰明显降低。到了500、1 000次的时候，随机值的干扰很小。两者在最优节点数的M-MSE相差仅0.000 005，可忽略不计。训练的M-MSE在1~80个隐层节点总体呈逐级下降趋势。1~4个隐层节点对应的M-MSE呈指数级递减，4~80个隐层节点对应的M-MSE递减趋势逐步放缓。测试的M-MSE在1~4个隐层节点对应M-MSE变化趋势与训练的M-MSE走势一致；而在5个隐层节点以后对应M-MSE的变化幅度较小；在21个隐层节点左右，对应的M-MSE降至最小；在40个隐层节点以后对应的M-MSE快速增加。

综合以上规律，同时考虑内存和计算成本等因素，确定该模型最佳隐层节点数为21个，最佳重复训练次数为500次。

将前92组数据的TP自动监测值、Turb、藻密度、Chl-a作为模型的训练输入数据集，TP实验室监测值作为训练输出数据集，隐层节点数设为21，建立模型，重复训练500次。将后12组数据作为测试模型。经过模型训练和测试，试验用时较短为4.4 s。模型训练的M-MSE为0.000 073 5，模型测试的M-MSE为0.000 103。在P值小于0.01时，相关系数为0.881，具有显著相关性。模型训练的结果见图4，模型测试的结果见表2。由模型测试值和实验室监测值的差值来看，其绝对误差为−0.017~0.012 mg·L⁻¹，相较自动监测值和实验室监测值的绝对误差为−0.021~0.084 mg·L⁻¹，绝对误差降幅较大。相对误差在30%以内的数据有11个，超过30%的数据有1个，为40%，但相较测试前的相对误差有大幅降低。比较模型测试前后相对误差的绝对值，除第12个数据相对误差略有升高外，其余相对误差的降幅为4%~103%，相对误差总体降幅较大。因此，经过模型修正的TP自动监测数据已大大降低了其他因素的干扰，模型测试值更接近实验室监测值。

模型测试中第8组和第11组数据误差≥30%。这2组数据中，Turb分别为23 NTU和26 NTU，已有研究^[24]表明水质浊度值大于80 NTU时才会对TNP分析仪(日本岛津)的监测结果产生明显干扰；藻密度分别为368×10⁴和387×10⁴个·L⁻¹，相较于2019年度太湖蓝藻预警期间湖体藻密度均值(1 218×10⁴个·L⁻¹)，水源地的藻密度相对较低。因此，Turb和藻密度并不是导致这2组数据偏差较大的原因。TP的测定可能受到其他因素的影响，例如TP分析中磷钼蓝络合物的强吸附能力会导致实验用的玻璃器皿及比色皿必须充分酸泡，否则容易产生干扰；另外，实验中大多数玻璃器皿中含有的少量硼硅酸盐会在显色时产生痕量硅钼蓝，引入正误差^[25]。

1)太湖东部湖区水源地自动监测TP数据和实验室TP数据偏差较大，受Turb、藻密度、Chl-a等影响，TP自动监测数据的合格率仅为52.9%，严重影响TP水质自动监控预警系统的发挥。

2)通过试触法确定ELM隐层节点数和多次训练求均值的方法可减少随机产生输入权值和阈值所导致的模型误差，提高了模型的准确度和可重复性。经过IELM修正的TP自动监测数据与实验室数据的偏差明显降低。因此，将极限学习机算法嵌入到自动监测系统中修正TP自动监测数据，可有效提升数据的准确性，使其真实较为地反映TP实际情况，为管理决策及水质预警提供可靠数据支撑。