Processing math: 100%
高级搜索

基于LUR模型的PM2.5浓度空间分布监测及分析

,  ,  , 

downloadPDF

上一篇

下一篇

王睿哲, 胡荣明, 李朋飞, 周晨. 基于LUR模型的PM2.5浓度空间分布监测及分析[J]. 环境工程学报, 2020, 14(10): 2843-2852. doi: 10.12030/j.cjee.201912156
引用本文: 王睿哲, 胡荣明, 李朋飞, 周晨. 基于LUR模型的PM2.5浓度空间分布监测及分析[J]. 环境工程学报, 2020, 14(10): 2843-2852. doi: 10.12030/j.cjee.201912156
shu
WANG Ruizhe, HU Rongming, LI Pengfei, ZHOU Chen. Monitoring and analysis of PM2.5 concentration spatial distribution based on LUR model[J]. Chinese Journal of Environmental Engineering, 2020, 14(10): 2843-2852. doi: 10.12030/j.cjee.201912156
Citation: WANG Ruizhe, HU Rongming, LI Pengfei, ZHOU Chen. Monitoring and analysis of PM2.5 concentration spatial distribution based on LUR model[J]. Chinese Journal of Environmental Engineering, 2020, 14(10): 2843-2852. doi: 10.12030/j.cjee.201912156
shu

基于LUR模型的PM2.5浓度空间分布监测及分析

  • 西安科技大学测绘科学与技术学院，西安 710054

    • 作者简介: 王睿哲(1996—)，男，硕士研究生。研究方向：大气污染防治。E-mail：840801221@qq.com
    通讯作者: 胡荣明(1969—)，男，博士，教授。研究方向：地理信息系统开发与应用。E-mail：rmhu2007@163.com; 
  • 基金项目:
    国家自然科学基金资助项目(41977059)

  • 中图分类号: X531

Monitoring and analysis of PM2.5 concentration spatial distribution based on LUR model

  • College of Geomatics, Xi'an University of Science and Technology, Xi'an 710054, China

    • Corresponding author: HU Rongming, rmhu2007@163.com ; 

摘要

  • 摘要: 为有效解决传统监测技术无法获取城市内部高分辨率PM2.5浓度空间分布情况的问题，基于土地利用回归(land use regression，LUR)模型，以关中平原城市群为例模拟其PM2.5空间分布状况，通过获取研究范围内54个监测站点的PM2.5浓度数据，结合土地利用类型、气象、地形、植被指数、人口密度、交通和污染源等因素，分别建立春、夏、秋、冬及年均5个LUR模型。结果表明：LUR模型调整后各季节及年平均值的R2分别达到0.831 (春)、0.817 (夏)、0.874 (秋)、0.857 (冬)、0.900 (全年平均)，5种模型拟合度均较好；采取交叉互验的方法进行了精度检验，显示5种模型的平均精度均达到80.4%，说明LUR模型在模拟关中平原城市群PM2.5浓度空间分布时适用性良好。模拟结果显示，研究区各季节的PM2.5浓度在空间分布上大致相同，呈现出东部高、西部低的明显特征，且空间分布状况受地形因素的影响较大。但在浓度均值的季节变化上则具有夏季低、冬季高的明显差异。本研究结果可为关中平原城市群PM2.5污染防治提供科学依据，亦可为城市内部PM2.5浓度空间分布数据的获取提供新思路。
    Abstract: In order to effectively solve the problem that the traditional monitoring technology cannot obtain the high-resolution spatial distribution of PM2.5 concentration in the city, the Guanzhong plain city group was taken as an example to simulate its PM2.5 spatial distribution status based on the land use regression (LUR) model. The 5 LUR models for spring, summer, autumn, winter and an annual average were built through obtaining PM2.5 concentration data of 54 monitoring stations in the study range and combining the factors such as land use type, meteorology, terrain, vegetation index, population density, traffic and pollution sources. The results showed that the adjusted R2 of each season and annual average of the LUR model reached 0.831 (spring), 0.817 (summer), 0.874 (autumn), 0.857 (winter), 0.90 (annual average), respectively, and better fitting levels occurred for the five models. A cross-examination method was used to carry out the accuracy test, and the average accuracy of the five models reached 80.4%, indicating that the LUR model had good applicability when simulating the spatial distribution of PM2.5 concentration in the Guanzhong plain city group. The simulation results showed that the PM2.5 concentration in each season of the study area was roughly same in spatial distribution with the significant characteristics of high in the east, low in the west, and obvious distribution trends along the altitude. However, there was a clear difference of low in summer and high in winter for the seasonal change of the mean concentration. The results of this study can provide a scientific basis for the prevention and control of PM2.5 pollution in the Guanzhong plain city group, and can also provide new ideas for obtaining the spatial distribution data of PM2.5 concentration within the city.

  • 随着染料工业的快速发展和新型助剂的不断使用，导致印染废水变得越来越难处理[1]。2018年，江苏省颁布《太湖地区城镇污水处理厂及重点工业行业主要污染物排放限制》(DB 32-2018)，新标准对染整行业废水提出了更加严格的排放要求。新标准明确规定了太湖流域的一、二级保护区内印染废水处理厂出水COD、TN、TP和NH3-N浓度应分别低于40、10、0.3和3 mg·L−1，并将在2021年1月起实施。

    有研究[2]表明，AB法的A段可以通过微生物的快速吸附作用来实现对印染废水中颗粒态有机物的高效去除，其具有较强的抗冲击负荷能力。好氧MBBR系统的生物膜载体使其具有高生物量和丰富的生物种类，可提高活性污泥法对污染物的降解能力，特别在降解某些难降解污染物(如双氯芬酸)方面比活性污泥能力更强[3]。混凝沉淀池可通过投加混凝剂和絮凝剂来实现强化去除TP和COD的目的。硫自养脱氮滤池可利用脱氮硫杆菌将硝酸盐氮还原为氮气[4]。活性焦滤池作为深度处理工艺可以有效地吸附大多数高分子有机物，进一步去除印染废水的色度和气味，以保证符合更高标准的排放要求[5]。

    本研究针对印染废水进水COD高、难生物降解、色度高、有机组分复杂等特点，结合企业提标改造的实际需求，在前期小试实验结果的基础上，搭建了以生物吸附-MBBR-硫自养反硝化-活性焦滤池为主体工艺的印染废水处理中试系统，启动并优化了中试运行的参数，以达到较好的污染物去除效果；考察了各工艺单元对污染物的去除效果及对有机物的去除特性，并通过分析不同运行参数下微生物菌群结构，利用高通量测序技术对接种污泥、生物吸附段和MBBR生物膜中的微生物群落进行了解析，探究了印染废水处理效能与菌群结构的关系，分析了该工艺的经济可行性，为其工程化应用提供参考。

    1.   材料与方法

    1.1   实验用水

    实验中使用的印染废水来自某印染园区废水处理厂初沉池出水，该厂废水处理量为6×104 t·d−1，进水水质指标如表1所示。

    表 1  进水主要水质指标的检测结果
    Table 1.  Test results of main water quality indicators mg·L−1
    实测数值与均值CODTNTPNH3-N-NSS
    实测数值482~90220.5~30.82.3~4.211.9~20.66.8~11.3263~815
    均值65323.93.315.48.6403
     | Show Table
    DownLoad: CSV

    1.2   中试装置

    实验装置工艺流程及中试装置见图1和图2。中试反应器的材质为碳钢，设计参数见表2。生物吸附池设计参数：HRT为1 h、SRT为2 d、DO为0.3 mg·L−1、MLSS控制在7 000 mg·L−1。MBBR池设计参数：SRT为20 d、DO为7 mg·L−1、MLSS维持在5 000 mg·L−1。硫自养脱氮滤池HRT为0.5 h，片状硫磺填料购自于郑州凯盈化工有限公司。活性焦柱的HRT为0.5 h，各单元进水方式均为下进上出。

    图 1  组合工艺流程图
    Figure 1.  Flow diagram of combined processes
    下载: 全尺寸图片 幻灯片
    图 2  中试装置图
    Figure 2.  Diagram of pilot test device
    下载: 全尺寸图片 幻灯片
    表 2  中试装置设计参数
    Table 2.  Design parameters of pilot test device
    功能单元设计停留时间/h实际池容/m3长(或直径)/m宽/m高/m池形
    生物吸附池19.81.51.54.35矩形
    中间沉淀池1.510.52.8—4.35圆柱形
    MBBR池10702.32.34.35矩形
    二沉池2.517.53.2—4.35圆柱形
    混凝沉淀池0.85.62.31.84.35矩形
    硫自养反硝化滤池0.50.63.2—2圆柱形
    活性焦吸附池0.50.63.2—2圆柱形
     | Show Table
    DownLoad: CSV

    1.3   实验运行阶段

    实验运行主要分为3个阶段：第1阶段(1~20 d)为启动阶段；第2阶段(20~80 d)为参数优化阶段，通过优化HRT、DO及加药条件，得到组合工艺的最佳污染物性能；第3阶段(80~100 d)为稳定阶段，在最优参数下运行中试系统，验证系统处理效果的稳定性。同时为研究该高效低耗组合工艺的微生物菌群特征，每天监测进出水常规污染物指标，周期性采集各生物池污泥样本，进行污泥菌群结构测试。中试系统各阶段运行参数见表3

    表 3  中试系统各阶段运行参数
    Table 3.  Operational conditions of combined process
    运行阶段运行时间/d生物吸附池MBBR池硫自养反硝化滤池活性焦柱
    DO/( mg·L-1)HRT/hDO/( mg·L-1)HRT/hHRT/hHRT/h
    启动阶段0~60.31510——
    7~170.3151022
    18~200.315100.50.5
    参数优化阶段21~270.315100.50.5
    28~350.31.25120.50.5
    36~470.31.55150.50.5
    48~510.31.25120.50.5
    51~560.61.251211
    57~6011.251222
    60~6711.231042
    67~7311.251042
    73~7911.271042
    稳定阶段80~10011.271211
     | Show Table
    DownLoad: CSV

    1.4   常规指标检测方法

    COD、NH3-N、TN、TP等指标采用文献中的方法[6]测定。

    1.5   三维荧光分析

    将待测样品置于岛津总有机碳分析仪上，检测总有机碳含量,用去离子水稀释，直到总有机碳浓度低于10 mg·L−1，采用日立F7000荧光分光光度计进行三维荧光(excitation emission matrix spectra，3D-EEM)测试。本实验以10 nm为增量，激发波长为200~400 nm，发射波长为280~500 nm，扫描速度为12 000 nm·min−1。最后使用Origin软件对三维荧光光谱数据进行处理[7]。

    1.6   傅里叶红外光谱分析

    采用傅里叶红外光谱(fourier transform infrared spectroscopy，FT-IR)对化合物进行定性分析，分析光谱图中的出峰位置以判断样品中可能含有的官能团结构[8]。实验采用红外光谱仪(VERTEX 70型，德国)[9]，波数为4 000~400 cm−1，实验前将水样在干燥机中进行风干，然后将风干后的样品磨成粉末，最后利用红外光谱仪进行扫描。

    1.7   GC-MS分析

    样品预处理采用固相萃取方式，首先依次用5 mL二氯甲烷和10 mL甲醇清洗和活化固相萃取柱，进样后依次用4 mL甲醇/乙酸乙酯(体积比为50∶50)和2 mL含1.7%甲酸的甲醇/乙酸乙酯(体积比为50∶50)洗脱，最后采用氮气进行吹脱，定容样品至1 mL[10]。

    采用美国赛默飞世尔科技有限公司的气相色谱-质谱联用仪(gas chromatography-mass spectrometer，GC-MS)进行实验，仪器型号为TSQ8000，色谱柱为DB-35毛细管色谱柱[11]。

    1.8   微生物菌群多样性分析

    采用OMEGA E.Z.N.A. Soil DNA Kit(美国 Omega Bio-tek公司)DNA抽提试剂盒对污泥样品种的DNA进行提取，将DNA产物作为模板，采用细菌16S rDNA扩增的通用引物341F(5′-CCTACGGGNGGCWGCAG-3′)和785R(5′-GACTACHVGGGTATC TAATCC-3′)进行2轮扩增及PCR产物纯化，PCR的反应扩增体系为25 μL，成分为2.5 μL的Taq Buffer(10×Ex)缓冲液、1 μL的dNTP、0.5 μL的正反向引物、0.1 μL的Takara Ex Taq聚合酶和10 ng的DNA，加超纯水至25 μL，混匀、离心。第1轮PCR反应条件为：94 ℃变性3 min，94 ℃变性10 s，55 ℃退火15 s，在72 ℃延伸30 s，共循环20次，最后于72 ℃保持7 min。PCR反应的第1轮产物纯化后直接进行第2轮扩增纯化，其反应条件为：94 ℃变性3 min，94 ℃变性10 s，然后55 ℃退火15 s，在72 ℃延伸30 s，总共循环5次，最后于72 ℃保持7 min。第2轮实验结束后，将样品置于-20 ℃条件下保存[12]，后续进行Illumina Miseq测序，本实验中数据库的建立是在上海晶能生物有限公司完成的。

    2.   结果与讨论

    2.1   污染物去除效果

    组合工艺对COD的去除效果如图3所示。可以看出，进水COD为490~1900 mg·L−1时，进水波动较大，在启动阶段，出水COD为90~160 mg·L−1，去除率为70%左右。生物吸附池可去除COD约100~300 mg·L−1，经过MBBR池处理后，COD进一步下降，MBBR池出水COD约为180~200 mg·L−1。在后续进行混凝沉淀处理时，可进一步去除颗粒态COD，混凝沉淀池出水COD约为100~140 mg·L−1。由于硫自养反硝化反应属于自养反应，不利用外源碳源，因此，后续硫自养反硝化池整体对COD基本没有去除效果。成功启动中试后，调整各个单元的DO和HRT，确定整套中试装置的最佳运行条件。经调试后，确认最佳运行参数，并以最优参数稳定运行20 d，在该阶段内本套工艺对COD的去除效率达到88%左右，出水COD约为15~28 mg·L−1，稳定达到DB 32-2018新标准中COD的排放限值(40 mg·L−1)。

    图 3  中试系统对COD的去除效果
    Figure 3.  COD removal by the pilot test system
    下载: 全尺寸图片 幻灯片

    生物吸附-MBBR-硫自养反硝化-活性焦滤池工艺是通过MBBR池在好氧条件下可将进水中的氧化转化为硝态氮，再由硫自养反硝化滤池进行反硝化，进一步去除硝态氮，从而达到较好的脱氮效果。图4为组合工艺对氮的去除效果。可以看出，进水TN浓度为13.08~30.59 mg·L−1，平均值约为21.94 mg·L−1，启动阶段MBBR池中填料并未完全挂膜成功，且硫自养反硝化菌驯化效果较差，出水TN浓度约为4.58~11.37 mg·L−1。经过后续运行参数调整后，在生物吸附池的DO和HRT分别为1 mg·L−1和1.2 h，MBBR池的DO和HRT分别为7 mg·L−1和12 h，硫自养反硝化滤池和活性焦滤池的HRT分别1 h 的条件下，系统脱氮效果达到最佳。二沉池出水NH3-N浓度低至0 mg·L−1，最终出水TN浓度稳定维持在5 mg·L−1以下,稳定达到DB 32-2018新标准中TN的排放限值(10 mg·L−1)。

    图 4  中试系统对氮的去除效果
    Figure 4.  Nitrogen removal by the pilot test system
    下载: 全尺寸图片 幻灯片

    图5为组合工艺对磷的去除效果。可以看出，进水中TP浓度为2.12~4.98 mg·L−1，由于印染废水中磷含量较市政污水中处于较低水平，因此，本工艺中采用完全化学除磷的方式进行除磷，本实验选取PAC作为除磷药剂。在启动和参数优化阶段，出水TP浓度为0.08~1.53 mg·L−1，通过对运行参数的优化，确定最佳除磷药剂投加量为50 mg·L−1，且在稳定运行阶段出水TP浓度下降明显，出水TP约为0.03~0.29 mg·L−1，出水稳定达到DB 32-2018新标准中TP的排放限值(0.30 mg·L−1)。

    图 5  中试系统对TP的去除效果
    Figure 5.  TP removal by the pilot test system
    下载: 全尺寸图片 幻灯片

    2.2   三维荧光结果分析

    三维荧光光谱可以通过其荧光强度的变化来体现相对物质的变化规律[13]，实验结果如图6所示。进水、生化池出水和混凝沉淀池出水中均出现2类明显的荧光峰，分别为类蛋白荧光峰、类富里酸荧光峰。类蛋白荧光峰位于Ex/Em=(265~295) nm/(310~345) nm，其中又包含2种荧光峰，分别为类色氨酸荧光峰和类酪氨酸荧光峰。类色氨酸荧光峰位于Ex/Em=(265~285) nm/(310~330) nm，类酪氨酸荧光峰位于Ex/Em=(275~295) nm/(325~345) nm；类富里酸荧光峰位于Ex/Em=(240~270) nm/(370~440) nm，其中也包含2类荧光峰，分别为紫外类富里酸荧光峰和可见类富里酸荧光峰。紫外类富里酸荧光峰位于Ex/Em=(235~245) nm/(330~370) nm，可见类富里酸荧光峰位于Ex/Em=(250~255) nm/(445~465) nm，未检测出类腐殖酸荧光峰。由此可知，印染废水中以类富里酸和类蛋白质物质为主。类蛋白和类富里酸类物质的荧光峰强度从进水至出水呈现明显降低趋势，说明经过生化处理及混凝沉淀工艺能有效去除该类有机物。出水中酪氨酸/色氨酸类物质仍然部分残留，这说明该类物质为惰性物质，较难被生物降解或吸附降解[14]，因此，在出水中仍保留一定的荧光强度。

    图 6  各工艺段出水的三维荧光特征
    Figure 6.  Three-dimensional fluorescence characteristics of the effluent from each process section
    下载: 全尺寸图片 幻灯片

    2.3   FT-IR结果分析

    傅里叶红外光谱分析(FT-IR)可通过分析有机化合物的分子结构，从而揭示有机污染物的去除特性[15]。如图7所示，印染废水经由二级处理和深度处理后，各样品的特征吸收峰出峰位置基本没有发生变动，其中代表性官能团主要分为以下几类，在3 500~3 350 cm−1处有较明显的C—OH的对称伸缩振动谱带，这说明水样中糖类有机物质较多，且该类物质较易被降解去除[16]；在1 500~1 750 cm−1处发现有较弱的不饱和C=O双键的伸缩振动吸收峰，在环境演变过程中，这些C=O不饱和键会逐渐转化为醛、酮、羧酸、酯类等物质，这说明可能存在含有氨基基团的酯类长链有机物质或酰胺类化合物，其可能为某类微生物代谢产物，这与表4中分析检测出的有机物成分一致；在1 400 cm−1处存在明显的C—O—C的伸缩振动峰，这说明可能存在某类染料中间体(酯类物质)[17]，由于炭基吸附剂对该类疏水性酯类物质有较好的吸附效果，因此，经过活性焦吸附池后该类峰强度明显减弱；在1 175 cm−1处发现C—O的伸缩振动峰，该类峰强度并未发生显著变化，这说明存在某类醇类物质，其难以被中试系统降解。

    表 4  印染废水及各处理工段废水中的有机物
    Table 4.  Organic compounds in raw wastewater and effluent from each treatment section
    进水生物处理出水混凝沉淀池出水活性焦出水
    邻苯二甲酸二丁酯N-甲基三氟乙酰胺N-甲基三氟乙酰胺N-甲基三氟乙酰胺
    2-乙基己醇2,4-二叔丁基酚2,4-二叔丁基酚2,4-二叔丁基酚
    异喹啉邻苯二甲酸二丁酯油酸酰胺2-苯基-2-丙醇
    N-甲基苯胺2-苯基-2-丙醇2-苯基-2-丙醇邻苯二甲酸正丁异辛酯
    2,4′-二氟二苯甲酮油酸酰胺邻苯二甲酸丁基酯
    2,6-二氯-1,4-苯二胺4-巯基-1-丁磺酸
    苄醚2,2-二甲氧基丁烷
    2-[(2-乙己基)氧]-乙醇丙二醇甲醚醋酸酯
    油酸酰胺棕榈酸
    2,4-二叔丁基苯酚
    3-甲氧基-3-甲基丁醇
    异喹啉
    反-2-甲基环已醇
    4-甲磺酰基苯胺
     | Show Table
    DownLoad: CSV
    图 7  各工艺段出水的FT-IR图谱
    Figure 7.  FT-IR spectra of each process section
    下载: 全尺寸图片 幻灯片

    2.4   GC-MS分析

    为验证和确定印染废水中主要难降解有机物的成分，利用GC-MS检测分析了组合工艺各单元出水中所含的有机污染物。中试各工艺单元的有机物分析结果见表4。进水中主要含有14种物质，包括醇、酮、胺和苯类衍生物等。经二级处理后，废水中有机物种类减少5种，主要存在9种有机物质，其中，醇类物质、酮类物质及多种苯胺类和喹啉类物质得到降解。经过混凝沉淀处理后，有机污染物种类数量得到较大去除，其中酸类物质均被去除，表明该类物质虽较难被生物降解，但可通过投加药剂去除。在经过活性焦滤池深度处理后，出水中有机物成分无显著减少，说明活性焦滤池之前的处理系统对有机物已达到了较好的去除效果。此外，发现出水中存在2,4-二叔丁基酚和N-甲基三氟乙酰胺成分，这2类物质广泛存在于各工艺单元，难以被系统去除，为该印染废水中的难降解特征有机污染物。

    2.5   微生物菌群分析

    为探究中试系统各单元微生物菌群结构与有机物的去除和脱氮除磷的内在关系，通过高通量测序技术对生物单元内微生物的群落结构进行解析。

    Alpha多样性分析用来研究细菌群落的丰富度和多样性[18]，包括Shannon、Chao、Ace、Simpson、覆盖率等统计学分析指数。接种污泥、生物吸附池、MBBR池和硫自养反硝化段微生物多样性指数分析如表5所示。在不同反应器中的样品覆盖率均达到99%以上，表明本次测序结果真实地反映样品中微生物群落结构组成特征[19]。根据Chao、Ace指数结果可知，生物吸附池微生物丰富度最高，这可能与印染废水中污染物数量，以及微生物的增殖、适应和选择等生物学过程有关[20]，在生物吸附池的富集下，出现能适应其环境的微生物群落，使生物吸附池菌群丰富度最高。相比生物吸附池，MBBR池的微生物丰富度略微下降，这可能是因为吸附池内微生物菌群无法进入MBBR池，而且MBBR池的有机负荷率较低。与生物吸附池和MBBR池相比，硫自养反硝化滤池的微生物丰富度指数Chao和Ace，以及多样性指数Shannon和Simpson明显有所下降，这表明硫自养反硝化滤池内微生物种群种类和结构相对单一[21]。

    表 5  样品Alpha多样性指数
    Table 5.  Alpha-diversity of the samples
    样品OUT/个ChaoACEShannonSimpson覆盖率/%
    接种污泥9481 050.8151 069.8694.479 850.955 9199.686
    生物吸附池1 0851 206.1951 193.615.026 560.974 0199.682
    MBBR-11 0261 144.6841 143.1434.931 730.969 8199.684
    MBBR-21 0201 194.251 183.8824.627 10.951 3799.608
    硫自养池8541 095.2481 079.2183.373 990.822 4899.552
     | Show Table
    DownLoad: CSV

    在进行系统微生物群落组成分析时，为了探究在组合工艺中微生物群落组成与污染物去除的内在关系，进一步解析反应器内微生物的群落结构组成[22]。如图8所示，各个单元中污泥所含的微生物分属35个门，主要包括Proteobacteria(变形杆菌门)、Planctomycetes(链霉菌门)、Firmicutes(厚壁菌门)、Chloroflexi(绿弯菌门)、Bacteroidetes(拟杆菌门)和Actinobacteria(放线菌门)。其中Proteobacteria和Firmicutes是污水处理厂活性污泥系统和废水生物处理中的主要菌门，具有可降解有机物及脱氮除磷的功能，因此，整套工艺具有较好去除COD及脱氮除磷的功能[23]。由于接种污泥取自某印染废水处理厂好氧池，且生物吸附池和MBBR池均为好氧环境，因此，三者优势菌门较为相似。由于进水中碳源含量较低且NO−3-N浓度高及缺氧生存环境使纯硫自养反硝化滤池内微生物多样性降低，种群种类和结构相对单一，Proteobacteria菌门所占比例高达60%左右，是所有菌门中的绝对优势菌门，该菌门在可能在废水污染物的去除过程中发挥重要作用。

    图 8  门水平的菌群组成
    Figure 8.  Microbial community composition at phylum level
    下载: 全尺寸图片 幻灯片

    实验进一步对样品中微生物群落组成的属水平进行分析，结果见图9。生物吸附池中Alkalibacter和Arcobacter菌属的相对丰度较高，其中Arcobacter菌属为一种较常见的致病菌属[24]，可能由于印染废水中成分较为复杂，生物吸附池直接与印染废水来水进行反应，受冲击可能性较大，但同时生物吸附池内微生物种类较为丰富，可在较短时间内进行吸附作用，降解印染废水中较易被去除的污染物。由于MBBR中填料的投加以及较好的曝气条件，Nitrospira菌属的相对丰度明显上升，赋予MBBR池较好的硝化能力，且悬浮填料可为微生物提供一个较好的黏附骨架，微生物可在填料上较好地挂膜生长，随着时间的累积，可形成较厚的生物膜，生物膜内部氧传质效果较差[25]，因此，在内部形成厌氧及缺氧区域，悬浮填料上存在Armatimonadetes_gp5等厌氧菌，其中部分菌属可进行反硝化反应。硫自养反硝化滤池中优势菌属是Georgfuchsia菌属和Ignavibacterium菌属，Georgfuchsia菌属具有降解多环芳烃(polycyclic aromatic hydrocarbon，PAHs)功能，这可能由于进水中仍含有大量芳香类难降解有机物，因此，该类菌属可在硫自养池中得到富集。Ignavibacterium菌属为常见的脱氮还原菌属[26]，可将NO−3-N还原生成N2，因此，硫自养池具有较好的脱氮功能。

    图 9  属水平的菌群组成
    Figure 9.  Microbial community composition at genus level
    下载: 全尺寸图片 幻灯片

    2.6   经济性分析

    中试装置运行成本主要包含除磷药剂、填料费用及设备运行电耗3部分。如表6和表7所示，反应器在100 d的运行期间内，处理总污水量约为12 500 m3，除磷药剂使用量约为2 500 kg，硫磺填料约为400 kg，活性焦填料约为300 kg。所选用的工业级硫磺市场价格为1 900 元·t−1，活性焦市场价格为7 600元·t−1，除磷药剂采用的聚合氯化铝市场价格为1 500元·t−1。因此，填料部分费用约为3 040 元，药剂消耗费用为3 750 元。主要的耗电设备为进水泵、鼓风机、回流泵和搅拌器，反冲泵电耗费用可忽略不计。进水泵功率为0.75 kW，搅拌器功率为1.5 kW，鼓风机功率为4 kW，回流泵功率为0.37 kW；综上所述，中试系统设备运行电耗成本费用合计1.287 元·t−1，设备运行药耗费用合计0.542 元·t−1，电价按照所在地工业用电价格(0.62 元·(kWh)−1)计，总电耗费用为16 125 元。相比而言，中试系统的处理成本约为1.83 元·m−3，显著低于实际污水处理厂(2.50 元·m−3)。由于该实验所选用泵的功率偏大，一定程度上增加了处理费用，优化后的水处理费用要低于该值，若该组合工艺被推广应用进而形成规模效应，可显著降低印染废水处理成本，节约社会资源。

    表 6  设备运行电耗费用
    Table 6.  Power consumption cost of equipment operation
    项目额定功率/kW数量/个运行成本/(元·t−1)
    进水泵0.7510.089
    鼓风机410.768
    搅拌器1.510.288
    回流泵0.3720.142
     | Show Table
    DownLoad: CSV
    表 7  设备运行药耗费用表
    Table 7.  Reagent cost of equipment operation
    项目使用量/kg单价/(元·t−1)运行成本/(元·t−1)
    除磷药剂2 5001 5000.300
    硫磺4001 9000.060
    活性焦3007 6000.182
     | Show Table
    DownLoad: CSV

    3.   结论

    1)中试运行结果表明，在生物吸附池(HRT为1.2 h，DO为1 mg·L−1)、MBBR池(HRT为12 h，DO为7 mg·L−1)、硫自养反硝化滤池(HRT为1 h)和活性焦滤池(HRT为1 h)的条件下，系统达到最优处理效能，出水COD、NH3-N、TP和TN浓度均可稳定达到DB 32-2018新标准中的污染物排放限值。

    2)由3D-EEM、FT-IR和GC-MS的分析结果可知，印染废水中以类富里酸和类蛋白质物质为主，系统出水中酪氨酸/色氨酸类物质仍然部分残留，这说明该类物质为惰性物质，较难被生物降解或吸附降解，典型官能团包括C—OH、C—O和C—O—C等，进水中主要含有14种物质，包括醇、酮、胺和苯类衍生物等，其中2,4-二叔丁基酚和N-甲基三氟乙酰胺成分为系统主要难降解有机物。

    3)通过16S rDNA基因序列分析发现，生物吸附池微生物丰富度最高，各工艺段中群落组成的菌门种类几乎相同，Proteobacteria和Bacteroidetes菌门是各工艺段的优势菌门，微生物群落结构门水平的分析表明了不同的反应器形成了不同的主导微生物，启动和优化过程中，微生物菌群结构发生着改变，整套工艺提供了较好的脱氮优势菌属。

    4)经核算，生物吸附-MBBR-混凝沉淀-硫自养-活性焦中试系统的处理成本约为1.83 元·t−1，低于实际污水处理厂(2.50 元·t−1)，若该组合工艺被推广应用进而形成规模效应，可显著降低废水处理成本，从而达到实现节能降耗的目的。

  • 图 1  研究区及监测站点分布

    Figure 1.  Study area and monitoring site distribution

    下载: 全尺寸图片 幻灯片

    图 2  研究区土地利用及道路

    Figure 2.  Land use and roads of the study area

    下载: 全尺寸图片 幻灯片

    图 3  PM2.5实测值-预测值散点

    Figure 3.  Scatter plots of the measured PM2.5 concentration versus the predicted one

    下载: 全尺寸图片 幻灯片

    图 4  关中平原城市群PM2.5浓度空间分布模拟图

    Figure 4.  Spatial distribution simulation of PM2.5 concentration in Guanzhong plain city group

    下载: 全尺寸图片 幻灯片

    表 1  PM2.5浓度与影响因子双变量相关分析结果

    Table 1.  Result of bivariate correlation analysis between PM2.5 concentration and impact factor

    自变量皮尔森相关系数P 自变量皮尔森相关系数P
    耕地面积3 km−0.392**0.003 人口密度0.310*0.021
    水体面积3 km−0.404**0.002 高程−0.859**0.000
    林地面积5 km−0.647**0.000 气压0.840**0.000
    草地面积5 km−0.514**0.000 温度0.823**0.000
    建设用地面积5 km0.789**0.000 风速−0.613**0.000
    裸地面积5 km−0.644**0.000 降水量−0.378**0.004
    一级道路长度5 km0.590**0.000 相对湿度−0.488**0.001
    二级道路长度5 km0.412**0.002 植被指数−0.415**0.002
    　　注：**表示在α=0.01下，相关性显著；*表示在α=0.05下，相关性显著。
    自变量皮尔森相关系数P 自变量皮尔森相关系数P
    耕地面积3 km−0.392**0.003 人口密度0.310*0.021
    水体面积3 km−0.404**0.002 高程−0.859**0.000
    林地面积5 km−0.647**0.000 气压0.840**0.000
    草地面积5 km−0.514**0.000 温度0.823**0.000
    建设用地面积5 km0.789**0.000 风速−0.613**0.000
    裸地面积5 km−0.644**0.000 降水量−0.378**0.004
    一级道路长度5 km0.590**0.000 相对湿度−0.488**0.001
    二级道路长度5 km0.412**0.002 植被指数−0.415**0.002
    　　注：**表示在α=0.01下，相关性显著；*表示在α=0.05下，相关性显著。
    下载: 导出CSV

    表 2  LUR模型结果

    Table 2.  LUR model results

    类型LUR模型R2调整后R2
    年均y=192.397−0.031x1−1.897x2−0.533x3+12.373x4+0.000 2x50.9130.900
    春季y=153.711−0.023x1−1.515x2−0.471x3+14.438x40.8460.831
    夏季y=189.304−0.016x1−2.381x2−0.000 06x60.8330.817
    秋季y=98.129−0.024x1−0.485x3−0.000 02x70.8830.874
    冬季y=215.589−0.052x1−1.549x3+0.000 04x50.8670.857
    　　注：y为PM2.5浓度；x1为高程；x2为相对湿度；x3为降水；x4为风速；x5为5 km缓冲区内建设用地面积；x6为5 km缓冲区内草地面积；x7为5 km缓冲区内林地面积。
    类型LUR模型R2调整后R2
    年均y=192.397−0.031x1−1.897x2−0.533x3+12.373x4+0.000 2x50.9130.900
    春季y=153.711−0.023x1−1.515x2−0.471x3+14.438x40.8460.831
    夏季y=189.304−0.016x1−2.381x2−0.000 06x60.8330.817
    秋季y=98.129−0.024x1−0.485x3−0.000 02x70.8830.874
    冬季y=215.589−0.052x1−1.549x3+0.000 04x50.8670.857
    　　注：y为PM2.5浓度；x1为高程；x2为相对湿度；x3为降水；x4为风速；x5为5 km缓冲区内建设用地面积；x6为5 km缓冲区内草地面积；x7为5 km缓冲区内林地面积。
    下载: 导出CSV

    表 3  模型精度对比

    Table 3.  Model accuracy comparison

    模型名称模型调整后R2平均相对误差/%均方根误差/(μg·m−3)线性拟合度
    年均LUR模型0.909.26.790.85
    春季LUR模型0.8312.97.850.77
    夏季LUR模型0.8212.17.520.81
    秋季LUR模型0.8713.27.210.79
    冬季LUR模型0.8612.77.480.80
    模型名称模型调整后R2平均相对误差/%均方根误差/(μg·m−3)线性拟合度
    年均LUR模型0.909.26.790.85
    春季LUR模型0.8312.97.850.77
    夏季LUR模型0.8212.17.520.81
    秋季LUR模型0.8713.27.210.79
    冬季LUR模型0.8612.77.480.80
    下载: 导出CSV
  • [1] 魏复盛, 胡伟, 滕恩江, 等. 空气污染对人体健康影响研究的进展[J]. 世界科技研究与发展, 2000(3): 14-18. doi: 10.3969/j.issn.1006-6055.2000.03.004
    [2] 吴健生, 谢舞丹, 李嘉诚. 土地利用回归模型在大气污染时空分异研究中的应用[J]. 环境科学, 2016, 37(2): 413-419.
    [3] HOEK G, BEELEN R, HOOGH K D, et al. A review of land-use regression models to assess spatial variation of outdoor air pollution[J]. Atmospheric Environment, 2008, 42(33): 7561-7578. doi: 10.1016/j.atmosenv.2008.05.057
    [4] 黄仁东, 仝慧贤, 刘抗, 等. 西安市PM2.5污染特征及其估测模型[J]. 环境工程学报, 2015, 9(6): 2974-2978. doi: 10.12030/j.cjee.20150671
    [5] 孙兆彬, 安兴琴, 陶燕, 等. 基于GIS和大气数值模拟技术评估兰州市PM10的人群暴露水平[J]. 中国环境科学, 2012, 32(10): 1753-1757. doi: 10.3969/j.issn.1000-6923.2012.10.004
    [6] 刘杰, 杨鹏, 吕文生. 北京大气颗粒物污染特征及空间分布插值分析[J]. 北京科技大学学报, 2014, 36(9): 1269-1279.
    [7] 陈辉, 厉青, 王中挺, 等. 利用MODIS资料监测京津冀地区近地面PM2.5方法研究[J]. 气象与环境学报, 2014, 30(5): 27-37.
    [8] CIOCǍNEA A, DRAGOMIRESCU A. Modular ventilation with twin air curtains for reducing dispersed pollution[J]. Tunnelling and Underground Space Technology, 2013, 37: 180-198. doi: 10.1016/j.tust.2013.03.012
    [9] 王敏, 邹滨, 郭宇. 基于BP人工神经网络的城市PM2.5浓度空间预测[J]. 环境污染与防治, 2013, 35(9): 63-66. doi: 10.3969/j.issn.1001-3865.2013.09.013
    [10] LEE J H, WU C F, HOEK G, et al. LUR models for particulate matters in the Taipei metropolis with high densities of roads and strong activities of industry, commerce and construction[J]. Science of the Total Environment, 2015, 514: 178-184. doi: 10.1016/j.scitotenv.2015.01.091
    [11] MAVKO M E, TANG B, GEORGE L A. A sub-neighborhood scale land use regression model for predicting NO2[J]. Science of the Total Environment, 2008, 398(1/2/3): 68-75.
    [12] KASHIMA S, YORIFUJI T, TSUDA T, et al. Application of land use regression to regulatory air quality data in Japan[J]. Science of the Total Environment, 2009, 407(8): 3055-3062. doi: 10.1016/j.scitotenv.2008.12.038
    [13] TANG R, BLANGIARDO M, GULLIVER J. Using building heights and street configuration to enhance intra urban PM10, NOx, and NO2 land use regression models[J]. Environmental Science&Technology, 2013, 47(20): 11643-11650.
    [14] 陈莉, 白志鹏, 苏笛, 等. 利用LUR模型模拟天津市大气污染物浓度的空间分布[J]. 中国环境科学, 2009, 29(7): 685-691. doi: 10.3321/j.issn:1000-6923.2009.07.003
    [15] 吴健生, 廖星, 彭建, 等. 重庆市PM2.5浓度空间分异模拟及影响因子[J]. 环境科学, 2015, 36(3): 759-767.
    [16] 焦利民, 许刚, 赵素丽, 等. 基于LUR的武汉市PM2.5浓度空间分布模拟[J]. 武汉大学学报(信息科学版), 2015, 40(8): 1088-1094.
    [17] 汉瑞英, 陈健, 王彬. 利用LUR模型模拟杭州市PM2.5质量浓度空间分布[J]. 环境科学学报, 2016, 36(9): 3379-3385.
    [18] 阳海鸥, 陈文波, 梁照凤. LUR模型模拟的南昌市PM2.5浓度与土地利用类型的关系[J]. 农业工程学报, 2017, 33(6): 232-239. doi: 10.11975/j.issn.1002-6819.2017.06.030
    [19] 赵佳楠, 徐建华, 卢德彬, 等. 基于RF-LUR模型的PM2.5空间分布模拟: 以长江三角洲地区为例[J]. 地理与地理信息科学, 2018, 34(1): 18-23. doi: 10.3969/j.issn.1672-0504.2018.01.004
    [20] 许刚, 焦利民, 肖丰涛, 等. 土地利用回归模型模拟京津冀PM2.5浓度空间分布[J]. 干旱区资源与环境, 2016, 30(10): 116-120.
    [21] 杨新兴, 尉鹏, 冯丽华. 大气颗粒物PM2.5及其源解析[J]. 前沿科学, 2013, 7(2): 12-19. doi: 10.3969/j.issn.1673-8128.2013.02.003
    [22] 徐敬, 丁国安, 颜鹏, 等. 北京地区PM2.5的成分特征及来源分析[J]. 应用气象学报, 2007(5): 645-654. doi: 10.3969/j.issn.1001-7313.2007.05.009
    [23] 成海容, 王祖武, 冯家良, 等. 武汉市城区大气PM2.5的碳组分与源解析[J]. 生态环境学报, 2012, 21(9): 1574-1579. doi: 10.3969/j.issn.1674-5906.2012.09.011
    [24] 慕建利, 梁生俊, 侯明全, 等. 近40年陕西省扬沙和沙尘暴天气[J]. 西北大学学报(自然科学版), 2005, 35(1): 109-112.
    [25] 万炜, 魏伟, 钱大文, 等. 土地利用/覆被变化的环境效应研究进展[J]. 福建农林大学学报(自然科学版), 2017, 46(4): 361-372.
    [26] 李玉玲, 刘红玉, 娄彩荣, 等. 江苏省PM2.5时空变化及土地利用影响研究[J]. 环境科学与技术, 2016, 39(8): 10-15.
    [27] 李会霞, 史兴民. 西安市PM2.5时空分布特征及气象成因[J]. 生态环境学报, 2016, 25(2): 266-271.
    [28] 李琛, 刘瑾, 王彦民. 气象因素对西安市城区空气质量的影响[J]. 干旱区资源与环境, 2017, 31(3): 83-88.
    [29] 段时光, 姜楠, 杨留明, 等. 郑州市冬季大气PM2.5传输路径和潜在源分析[J]. 环境科学, 2019, 40(1): 86-93.
    [30] 任浦慧, 解静芳, 姜洪进, 等. 太原市大气PM2.5季节传输路径和潜在源分析[J]. 中国环境科学, 2019, 39(8): 3144-3151. doi: 10.3969/j.issn.1000-6923.2019.08.002
    [31] 黄光球, 雷哲. 西安市大气颗粒物PM2.5的输送路径和潜在源分析[J]. 云南大学学报(自然科学版), 2019, 41(6): 1191-1200. doi: 10.7540/j.ynu.20190157
  • 加载中
    Created with Highcharts 5.0.7访问量Chart context menu近一年内文章摘要浏览量、全文浏览量、PDF下载量统计信息摘要浏览量全文浏览量PDF下载量2024-052024-062024-072024-082024-092024-102024-112024-122025-012025-022025-032025-040Highcharts.com
    Created with Highcharts 5.0.7Chart context menu访问类别分布DOWNLOAD: 3.6 %DOWNLOAD: 3.6 %HTML全文: 88.1 %HTML全文: 88.1 %摘要: 8.3 %摘要: 8.3 %DOWNLOADHTML全文摘要Highcharts.com
    Created with Highcharts 5.0.7Chart context menu访问地区分布其他: 83.8 %其他: 83.8 %Bangkok: 0.2 %Bangkok: 0.2 %Baoding: 0.1 %Baoding: 0.1 %Beijing: 6.0 %Beijing: 6.0 %Bucharest: 0.1 %Bucharest: 0.1 %Central: 0.1 %Central: 0.1 %Chang'an: 0.1 %Chang'an: 0.1 %Chashan: 0.1 %Chashan: 0.1 %Chongqing: 0.1 %Chongqing: 0.1 %Ewirgol: 0.1 %Ewirgol: 0.1 %Fenyang: 0.1 %Fenyang: 0.1 %Guangzhou: 0.1 %Guangzhou: 0.1 %Gulan: 0.1 %Gulan: 0.1 %Handan: 0.1 %Handan: 0.1 %Hangzhou: 0.1 %Hangzhou: 0.1 %Harbin: 0.1 %Harbin: 0.1 %Hyderabad: 0.1 %Hyderabad: 0.1 %Jinrongjie: 0.6 %Jinrongjie: 0.6 %Kunshan: 0.1 %Kunshan: 0.1 %Langfang: 0.1 %Langfang: 0.1 %Liverpool: 0.2 %Liverpool: 0.2 %Mountain View: 0.2 %Mountain View: 0.2 %New Taipei: 0.1 %New Taipei: 0.1 %Panjin: 0.4 %Panjin: 0.4 %Shanghai: 0.4 %Shanghai: 0.4 %Shatin: 0.1 %Shatin: 0.1 %Shenyang: 0.1 %Shenyang: 0.1 %Shenzhen: 0.1 %Shenzhen: 0.1 %The Bronx: 0.1 %The Bronx: 0.1 %Toronto: 0.2 %Toronto: 0.2 %Tsukuba: 0.1 %Tsukuba: 0.1 %Weinan: 0.1 %Weinan: 0.1 %Wuhan: 0.1 %Wuhan: 0.1 %Wulipu: 0.1 %Wulipu: 0.1 %Xi'an: 0.1 %Xi'an: 0.1 %Xiangtan: 0.1 %Xiangtan: 0.1 %Xincheng: 0.1 %Xincheng: 0.1 %XX: 3.0 %XX: 3.0 %Yuncheng: 0.1 %Yuncheng: 0.1 %Zhengzhou: 0.5 %Zhengzhou: 0.5 %上海: 0.1 %上海: 0.1 %内网IP: 0.1 %内网IP: 0.1 %北京: 0.6 %北京: 0.6 %北海: 0.1 %北海: 0.1 %昆明: 0.1 %昆明: 0.1 %杭州: 0.1 %杭州: 0.1 %武汉: 0.1 %武汉: 0.1 %深圳: 0.1 %深圳: 0.1 %温州: 0.1 %温州: 0.1 %芝加哥: 0.1 %芝加哥: 0.1 %西宁: 0.1 %西宁: 0.1 %西安: 0.1 %西安: 0.1 %贵阳: 0.1 %贵阳: 0.1 %郑州: 0.5 %郑州: 0.5 %长春: 0.1 %长春: 0.1 %长沙: 0.1 %长沙: 0.1 %阳泉: 0.1 %阳泉: 0.1 %其他BangkokBaodingBeijingBucharestCentralChang'anChashanChongqingEwirgolFenyangGuangzhouGulanHandanHangzhouHarbinHyderabadJinrongjieKunshanLangfangLiverpoolMountain ViewNew TaipeiPanjinShanghaiShatinShenyangShenzhenThe BronxTorontoTsukubaWeinanWuhanWulipuXi'anXiangtanXinchengXXYunchengZhengzhou上海内网IP北京北海昆明杭州武汉深圳温州芝加哥西宁西安贵阳郑州长春长沙阳泉Highcharts.com
WeChat 点击查看大图
图( 4) 表( 3)
计量
  • 文章访问数:  5461
  • HTML全文浏览数:  5461
  • PDF下载数:  76
  • 施引文献:  0
出版历程
  • 收稿日期:  2019-12-27
  • 录用日期:  2020-04-24
  • 刊出日期:  2020-10-10
王睿哲, 胡荣明, 李朋飞, 周晨. 基于LUR模型的PM2.5浓度空间分布监测及分析[J]. 环境工程学报, 2020, 14(10): 2843-2852. doi: 10.12030/j.cjee.201912156
引用本文: 王睿哲, 胡荣明, 李朋飞, 周晨. 基于LUR模型的PM2.5浓度空间分布监测及分析[J]. 环境工程学报, 2020, 14(10): 2843-2852. doi: 10.12030/j.cjee.201912156
shu
WANG Ruizhe, HU Rongming, LI Pengfei, ZHOU Chen. Monitoring and analysis of PM2.5 concentration spatial distribution based on LUR model[J]. Chinese Journal of Environmental Engineering, 2020, 14(10): 2843-2852. doi: 10.12030/j.cjee.201912156
Citation: WANG Ruizhe, HU Rongming, LI Pengfei, ZHOU Chen. Monitoring and analysis of PM2.5 concentration spatial distribution based on LUR model[J]. Chinese Journal of Environmental Engineering, 2020, 14(10): 2843-2852. doi: 10.12030/j.cjee.201912156
shu

基于LUR模型的PM2.5浓度空间分布监测及分析

    通讯作者: 胡荣明(1969—)，男，博士，教授。研究方向：地理信息系统开发与应用。E-mail：rmhu2007@163.com; 
    作者简介: 王睿哲(1996—)，男，硕士研究生。研究方向：大气污染防治。E-mail：840801221@qq.com
  • 西安科技大学测绘科学与技术学院，西安 710054
  • 收稿日期:  2019-12-27
  • 录用日期:  2020-04-24
  • 网络出版日期:  2022-09-02
基金项目:
国家自然科学基金资助项目(41977059)

摘要: 为有效解决传统监测技术无法获取城市内部高分辨率PM2.5浓度空间分布情况的问题，基于土地利用回归(land use regression，LUR)模型，以关中平原城市群为例模拟其PM2.5空间分布状况，通过获取研究范围内54个监测站点的PM2.5浓度数据，结合土地利用类型、气象、地形、植被指数、人口密度、交通和污染源等因素，分别建立春、夏、秋、冬及年均5个LUR模型。结果表明：LUR模型调整后各季节及年平均值的R2分别达到0.831 (春)、0.817 (夏)、0.874 (秋)、0.857 (冬)、0.900 (全年平均)，5种模型拟合度均较好；采取交叉互验的方法进行了精度检验，显示5种模型的平均精度均达到80.4%，说明LUR模型在模拟关中平原城市群PM2.5浓度空间分布时适用性良好。模拟结果显示，研究区各季节的PM2.5浓度在空间分布上大致相同，呈现出东部高、西部低的明显特征，且空间分布状况受地形因素的影响较大。但在浓度均值的季节变化上则具有夏季低、冬季高的明显差异。本研究结果可为关中平原城市群PM2.5污染防治提供科学依据，亦可为城市内部PM2.5浓度空间分布数据的获取提供新思路。

English Abstract

    全文HTML

  • 随着中国经济的高速发展，大气污染成为全社会所关注的问题。当大气污染物达到一定浓度时，会对人体的呼吸系统造成危害，其中PM2.5表现最为明显[1]。因此，对PM2.5浓度的监测及数据获取就显得尤为重要，但目前常用的监测方式均存在一些不足[2]，无法实现高分辨率PM2.5浓度空间分布制图。如实验设计监测成本较高、常规监测在监测站数目上得不到保证、车载移动监测的总体监测时间较短等。监测技术的不足为分析城市PM2.5时空分布特征及污染防治带来很大挑战[3]，国内外学者尝试通过构建模型的方法来解决问题。黄仁东等[4]利用统计学与多元回归分析法构建四季最优模型，模拟分析了西安市PM2.5污染特征；孙兆彬等[5]利用CMAQ空气质量模型，模拟出兰州市PM10月均浓度；刘杰等[6]应用MATLAB空间插值算法实现对北京市颗粒污染物的空间分布模拟；陈辉等[7]利用MODIS遥感影像反演AOD的方法建立模型，模拟出京津冀地区PM2.5浓度；此外，扩散模型[8]、神经网络[9]等方法也都被应用于大气污染物浓度模拟。然而，这些方法大都未将影响PM2.5浓度的各种因素考虑进去，会对模型模拟结果的解释能力及精度造成影响。LUR模型综合考虑各种影响因素对PM2.5浓度进行模拟，其精度、解释能力较其他方法更强，已成为模拟大气污染物浓度最有效的方法之一[2,10]。

    在欧美、日本等国家，LUR模型已被广泛使用，并在模拟城市PM2.5、NO2和NOx等污染物浓度空间分布方面取得良好效果[3,11-13]。我国学者对LUR模型的应用研究不多，多集中于对特定城市污染物浓度的模拟。陈莉等[14]应用该模型模拟了天津市PM10和NO2浓度的空间分布；吴健生等[15]、焦利民等[16]、汉瑞英等[17]及阳海鸥等[18]分别模拟了重庆市、武汉市、杭州市和南昌市的PM2.5浓度空间分布。然而，由于对区域尺度的PM2.5模拟所需数据量大，以及区域城市间污染传输等难题，只有少数学者开展过区域尺度的相关研究[19-20]。

    鉴于区域尺度PM2.5的模拟研究对区域联防联控机制有着重要指导意义，本研究以中国西北部关中平原城市群为例，利用LUR模型模拟其PM2.5浓度，探讨LUR模型在区域尺度上的适用性，并进一步构建最优LUR模型，为该区域PM2.5污染防治提供科学依据，也为城市内部PM2.5浓度空间分布数据获取提供新的思路。

1.   研究区域及方法

    1.1.   研究区概况

  • 关中平原城市群地处中国内陆中心，是我国雾霾及风沙多发的区域之一，包括西安、咸阳、宝鸡、渭南、铜川、天水以及商洛、临汾、运城、平凉、庆阳的部分区县等。在“一带一路”倡议的推动下，关中平原城市群的综合经济实力已位居中国内陆区域第二，但与此同时，也造成了区域内城市的空气质量恶化。据2017年全国365个城市的年均PM2.5浓度排名显示，该区域有5个城市的年均PM2.5浓度排在了全国前20。区域年平均PM2.5浓度为57.34 μg·m−3，超过国家二级标准60%(35 μg·m−3)，空气污染现状不容乐观。

    • 1.2.   LUR模型

  • LUR具有模拟精度高、考虑因素全面等特点，是模拟PM2.5浓度的有效方法。本研究主要利用SPSS 24.0与Arcgis10.2软件，构建PM2.5浓度与土地利用类型、地形、气象、道路交通、人口密度和污染源等相关因子的多元回归方程，即LUR模型。模型的基本形式通常包括1个因变量和2个或者2个以上自变量，计算方法见式(1)。

    式中：y为因变量，即PM2.5浓度值；x1， x2，···，xn为自变量即文中的影响因子；β0，β1，β2，···，βn为待定系数；α为随机变量。

    • 1.3.   建模方法

  • 首先，利用SPSS软件对PM2.5浓度与各类影响因子进行双变量相关性分析，并筛选去除与PM2.5浓度不显著相关(P>0.05)的影响因子。本研究生成的影响因子包括：土地利用类型(6类)、主要道路交通(4类)、污染源通过生成缓冲区的方式获取77(11×7)个影响因子；气象(5类)、植被指数、高程、人口密度等通过空间插值提取的方式获取8个影响因子，共计得到85(77+8)个影响因子。为避免后续多元线性回归方程中不同缓冲区下同类因子的共线性问题，采用吴健生等[2]提出的后向算法，即先找出每类影响因子中与PM2.5浓度相关性最高的影响因子，然后去除同类因子中与最高影响因子皮尔森相关系数大于0.6的因子。

    其次，将筛选后剩余的影响因子与PM2.5浓度值进行逐步线性回归，得到多元线性回归方程，即LUR模型，并采用留一交叉互验(leave-one-out cross validation)的方法对模型精度进行检验。然后利用Arcgis10.2软件生成5 km×5 km规则格网点，根据多元回归方程计算得到每个格网点的PM2.5浓度预测值。

    最后，通过克里金插值法(Kriging)，模拟出研究区的PM2.5浓度空间分布图。

2.   监测数据源及数据处理方法

    2.1.   PM2.5浓度数据

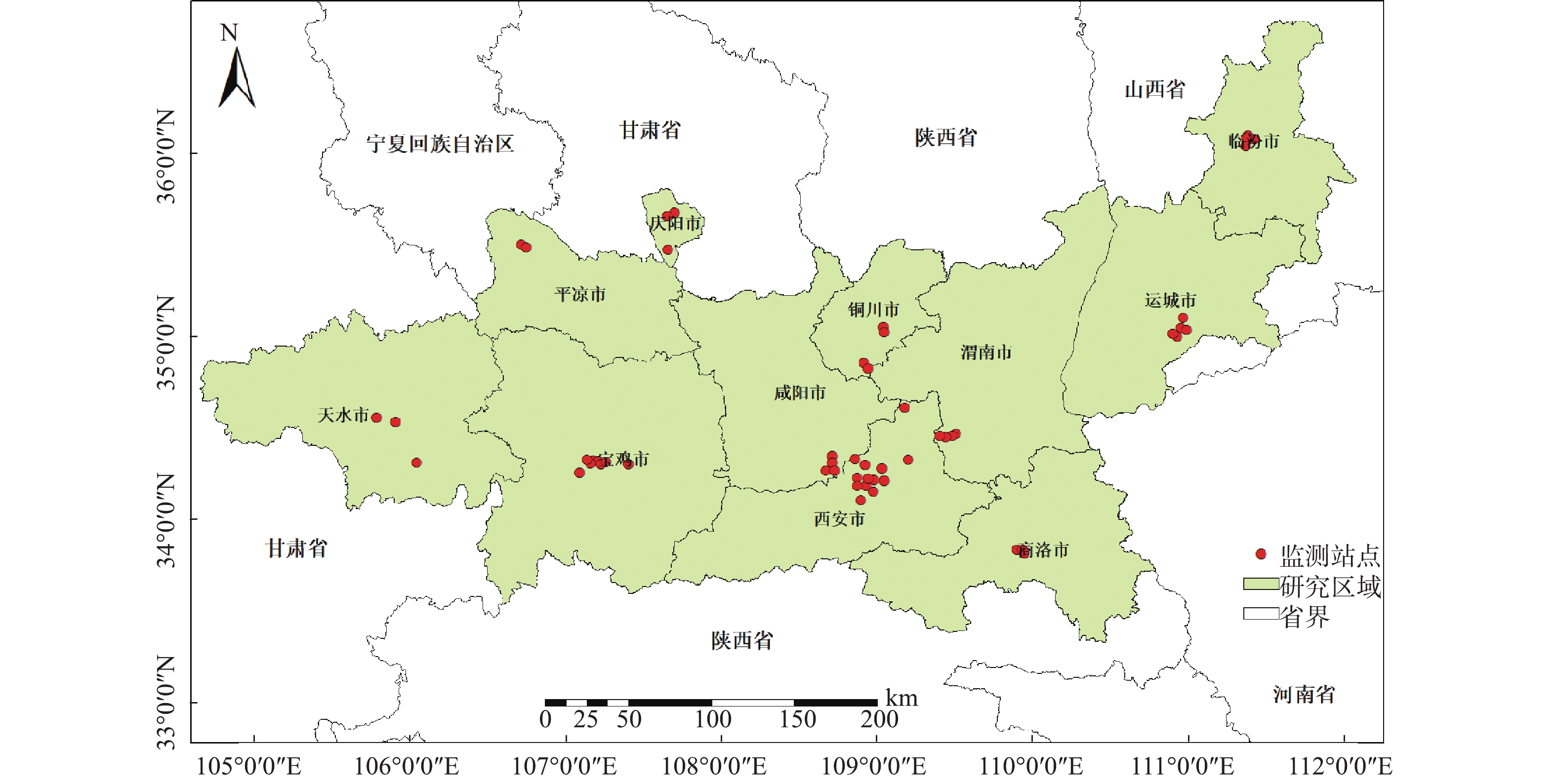
  • 采集2017年1—12月关中平原城市群范围内共计54个空气质量监测点的日均PM2.5浓度监测数据(数据来自中国环境监测总站http://www.cnemc.cn/)，对这些数据进行汇总统计，得到各监测站点年均及季节PM2.5浓度值，研究区范围及监测站点分布，结果如图1所示。

    • 2.2.   土地利用及道路数据

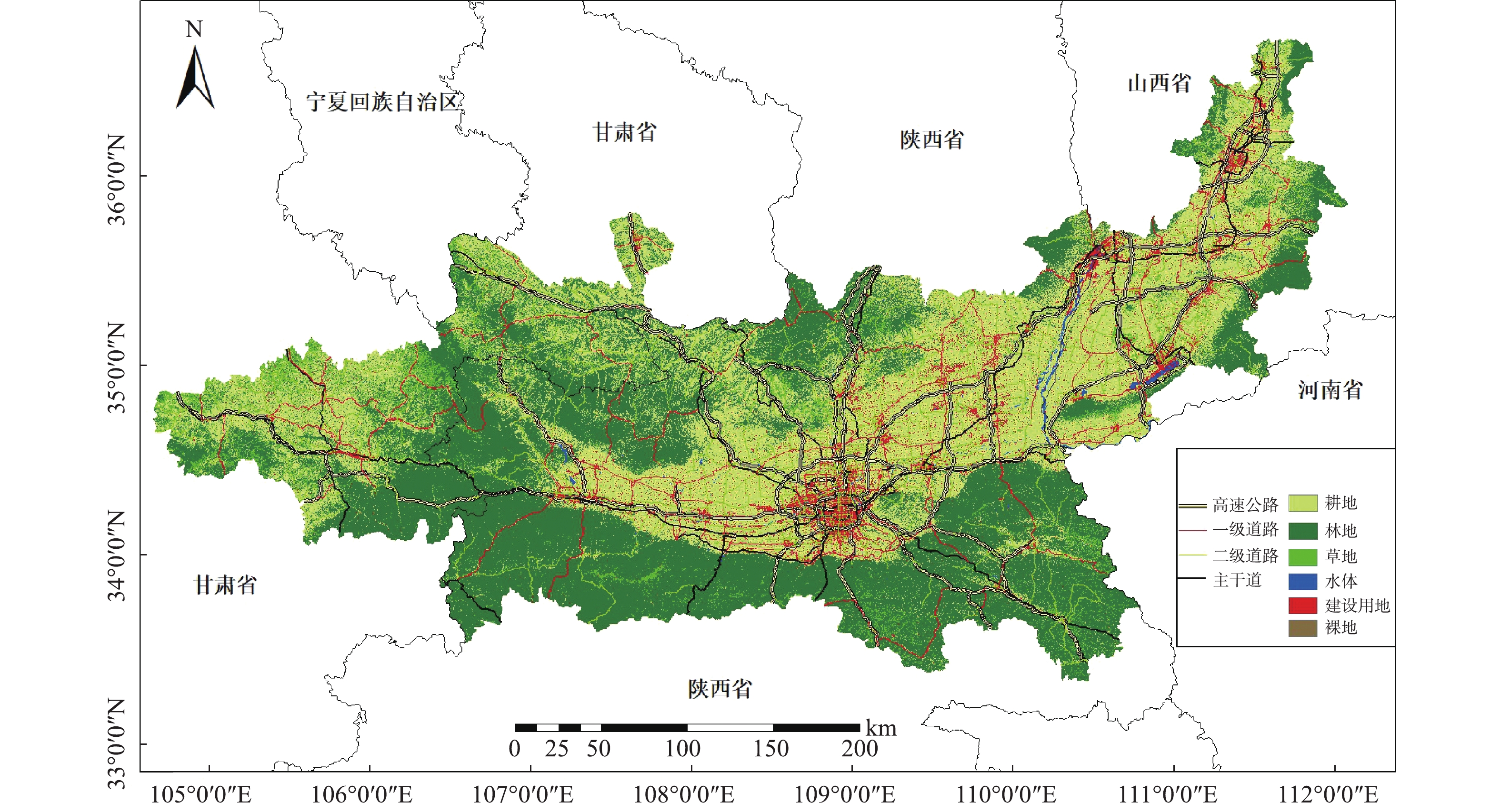
  • 土地利用数据为清华大学发布的2017年全球10 m分辨率土地利用数据集。该数据集将全球土地分为10大类。利用Arcgis10.2经拼接、裁剪和重分类等处理，并考虑各类型用地的面积及属性，将土地利用划分为耕地、林地、草地、水域、建设用地和裸地等6类，结果如图2所示。再以每个监测站点为中心，分别生成0.5、1、1.5、2、3、4和5 km的缓冲区，统计每种缓冲区中各类土地利用类型的面积，将得到的数据作为土地利用类型因子。道路数据来源于OpenStreetMap的矢量路网，提取研究区范围内高速公路、主干道、一级道路、二级道路等4类，并以监测站点为中心建立相同的缓冲区，通过空间叠加法统计得到每种缓冲区内各类道路的长度作为道路因子。

    • 2.3.   地形数据

  • 关中平原城市群东西海拔相差大，其复杂的地形会对PM2.5浓度产生一定的影响。本研究利用DEM数据表示研究区的地形地貌特征，从地理空间数据云上(http://www.gscloud.cn/)下载获取Aster GDEM数据，经拼接、裁剪得到研究区的DEM，并提取每个监测站点处的高程值作为地形因子。

    • 2.4.   气象数据

  • 从中国气象科学数据共享服务网，获取研究区范围内28个气象站点2017年的气象数据。选取的气象因子包括：平均大气压、平均降水量、平均气温、平均风速和相对湿度等5项。统计得到各站点气象要素的季节及年均值，并利用空间插值提取的方法，获取各监测站点位置处的气象要素值作为气象因子。

    • 2.5.   植被指数数据

  • 归一化植被指数(normalized difference vegetation index, NDVI)数据来源于NASA官方的MODIS数据，选取2017年1月至12月的MOD13A1产品数据。利用MODIS重投影工具 (MODIS reprojection tools, MRT)对该数据进行批量投影、拼接等预处理，然后采取最大值合成法(maximum value composite, MVC)进行数据合成，并裁剪得到研究区年NDVI栅格图，提取监测站点处的NDVI值作为植被指数因子。

    • 2.6.   人口密度数据与污染源数据

  • 人口密度数据采用中国科学院资源环境科学数据中心(http://www.resdc.cn/)所发布的2015中国人口分布公里网数据集。以监测站点处的栅格值表示该点的人口密度，作为人口密度因子。工业废气的排放是PM2.5重要来源之一[21-23]。从生态环境部官网上收集到研究区范围内约130个国家重点监测企业(废气)名单及地址信息，再以监测点为中心建立相同的缓冲区，统计每种缓冲区内污染源的个数作为污染源因子。

3.   结果与分析

    3.1.   PM2.5浓度与影响因子相关分析

  • 以年均PM2.5浓度为例，利用SPSS软件对其与各种影响因子进行双变量相关分析。根据模型筛选变量的方法，首先剔除与PM2.5浓度不显著相关的34个影响因子(P>0.05)。为有效避免后续LUR建模时不同缓冲区下同类影响因子的共线性问题，对自变量进行再次筛选，即先计算出同类影响因子中排序最高因子与其他因子之间的相关系数，然后剔除相关系数大于0.6的影响因子，最终得到16个影响因子。表1数据表明，PM2.5浓度与耕地、林地、水体、草地、裸地、高程、降水量、相对湿度、风速和NDVI等因子呈负相关；与建设用地、气压、温度、人口密度、道路长度和污染源个数等因子呈正相关。其中，PM2.5浓度与高程的相关系数最高，说明研究区PM2.5浓度受高程因素的影响最大。

    • 3.2.   模型构建及精度验证

  • 由于各季节气象条件的不同，可能造成影响PM2.5浓度的主导因素不同，故分别以春、夏、秋、冬及年均PM2.5浓度为因变量，同时获取相对应影响因子作为自变量，构建多元回归方程即LUR模型共5个，结果如表2所示。可以看出，最终进入5个LUR模型的影响因子不尽相同。在所有模型当中都包含了高程因子，说明对研究区年均及四季PM2.5浓度影响最大的是地形因素。此外，气象因素中相对湿度因子进入了年均、春和夏季的LUR模型；降水因子分别进入了年均、春、秋和冬季的LUR模型，风速因子则进入了年均及春季的LUR模型。说明在3个气象因子中，降水和相对湿度对研究区的PM2.5浓度影响较大，且对PM2.5浓度有消减作用，而风速对春季的PM2.5影响较大且会使其浓度增加，这与该地区春季扬沙天气频繁密切相关[24]；土地利用类型因素中5 km缓冲区内建设用地面积进入了年均及冬季的LUR模型、5 km缓冲区内草地面积和林地面积则分别进入了夏季和秋季的LUR模型。进一步分析模型方程发现，建设用地的增加对PM2.5浓度具有加剧作用，而草地、林地的增加对PM2.5浓度具有削减作用。这是由于土地利用类型的变化会引起地表反射率、粗糙度及植被覆盖度等地表物理性质的改变，从而影响区域内降水、湿度等气象条件，进而导致了PM2.5浓度出现差异[25-26]；另一方面也可能与冬季居民区供暖等人为因素有关。由表2中模型调整后的R2可知，5个LUR模型的R2都在0.8以上，表明LUR模型拟合度较好、解释能力较强，其中年均LUR模型R2达到了0.9，在所有模型当中为最好。

    采用交叉验证方法对模型的精度进行检验，并通过模型调整后R2、相对误差、均方根误差、线性回归拟合度4项指标，对5种模型的精度及稳定性进行评价。其中相对误差是指模拟值与实测值之间的偏移度，表示的是模型模拟结果的可靠程度；均方根误差是模拟值与实测值之间的偏差，它可以反映模拟结果的准确性；线性回归拟合度则表示模型的拟合精度，计算结果如表3所示。5种模型平均相对误差均值为12%，均方根误差均值为7.37 μg·m−3。对各监测站点的PM2.5浓度预测值与实际值进行线性回归(如图3所示)，发现LUR模型的线性拟合度分别为0.85(年均)、0.77(春)、0.81(夏)、0.79(秋)、0.80(冬)。因此，LUR模型在模拟关中平原城市群年均及季节PM2.5浓度时效果较好。经进一步对比，5种模型中年均LUR模型的各项精度指标均为最优，表明LUR模型在模拟研究区年均PM2.5浓度时效果最好，且模拟精度最高、模型最稳定性最强。

    • 3.3.   PM2.5浓度模拟

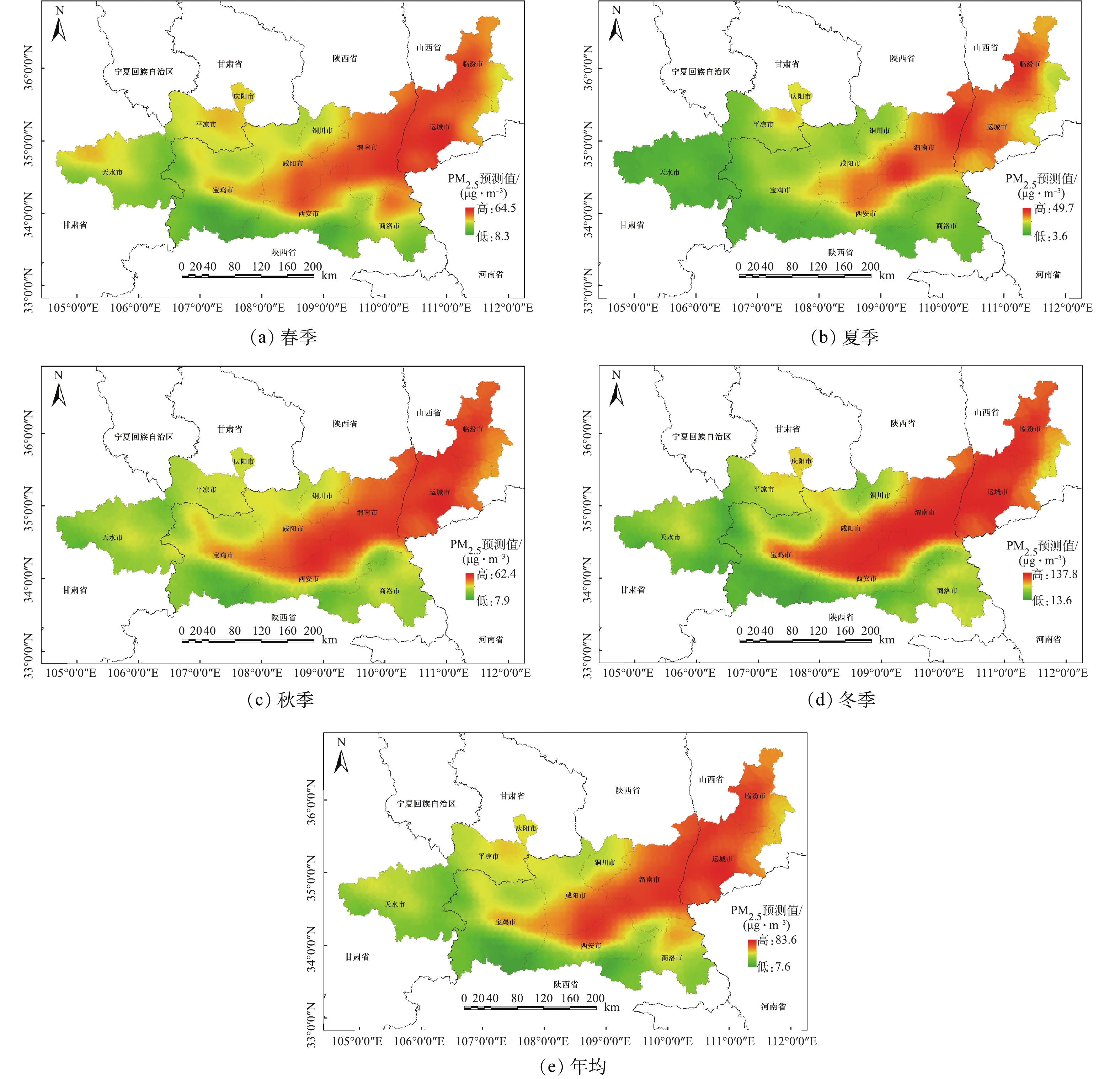
  • 为更加直观地分析关中平原城市群PM2.5空间分布特征，在研究区范围内生成5 km×5 km的格网，并计算出每个格网点相对应的影响因子数值，分别带入表2的多元回归方程式中，得到各格网点的PM2.5浓度值。然后通过采用Kriging插值法，模拟生成关中平原城市群各季节及年均的PM2.5浓度空间分布(图4)。如图4所示，各季节的PM2.5浓度均值变化有明显差异，具体表现为冬季(78.26 μg·m−3)>春季(37.47 μg·m−3)>秋季(34.58 μg·m−3)>夏季(21.28 μg·m−3)；另外，PM2.5浓度高值区范围随着季节变化而变化，由夏季的3个污染强点逐渐向四周扩散形成冬季连片状的污染区，这种现象主要由冬季逆温天气多发、建成区内集中供暖等原因所导致[27-28]；但各季节的PM2.5空间分布则大致相同，高值大多集中在西安、咸阳、渭南和运城等东部、北部地区，低值则多集中在天水、平凉、宝鸡以及商洛等西部、南部地区；研究区PM2.5浓度沿海拔走势分布明显，关中平原等低海拔的区域污染严重，而秦岭山地等高海拔区域污染较轻。

    LUR模型在一定程度上解释了该研究区PM2.5的浓度空间分布特征。研究区内海拔差异明显，地势高低起伏。关中平原中部及东部是人口、城市以及工业生产等主要集中的区域，空气污染相对较重。尤其是晋陕交界一带是煤炭等工业生产活跃的区域。据统计，这一区域内约有国家重点监测企业(废气)55家，大气污染物排放量大，空气污染最为严重。西部及南部地区靠近秦岭山地，植被覆盖度高，加上人口密度小、工业生产活动少等缘故，其空气质量相对较好。

    • 3.4.   基于LUR模型的PM2.5污染防治建议

  • 1) 完善区域联防联控机制。PM2.5的形成及来源复杂，对单一污染源及单一城市的控制很难从根本上减轻污染。一个城市的大气污染不仅与本地的自然、人为等因素有关，也与外来污染物传输密切相关[29-30]。以该区域重要城市西安为例，有超过50%的气流轨迹来自西北方向[31]。因此，从区域尺度上分析PM2.5空间分布，可进一步为建立完善区域联防联控机制提供可靠的信息支持，以便更好地解决城市大气污染。

    2) 实行污染分区监管。根据区域地理特征、气象条件及经济发展等因素的不同，将区域分为严重污染区及一般污染区，实施差异化控制管理，因地制宜地制定污染防治措施。尤其是针对关中平原东部及中部等污染严重的区域，相关政府部门应加快完善预警、约谈、问责工作机制。

    3) 实施季节性差异化防治。根据各季节LUR模型当中主要贡献因子的不同，实施有针对性的防治措施。如春夏季可通过道路洒水增加空气湿度减轻污染，据模型显示相对湿度每增加1%，PM2.5浓度会分别降低1.5 μg·m−3和2.3 μg·m−3；秋季可通过人工降雨或增加绿化减轻污染，据模型显示降水量每增加1 mm，PM2.5浓度会降低0.5 μg·m−3；冬季则可通过城区机动车限行、合理供暖以及人工降水降雪等措施减轻污染；模型显示降水量每增加1 mm，PM2.5浓度会降低1.5 μg·m−3。

    4) 强化污染源头控制。工业排放及燃煤使用是PM2.5最主要的来源之一，尤其是研究区东部晋陕交界煤炭工业发达，是关中平原大气污染最主要的源头，因此，该区域企业需要加大能源结构调整和节能减排力度，从源头上防治大气污染。

    本研究将LUR模型应用到区域尺度的PM2.5浓度空间分布模拟，通过对非监测点PM2.5浓度值的模拟，解决了传统监测方式中站点数量少、覆盖范围小和成本高等问题，并实现了高分辨率PM2.5浓度空间分布制图，且该模型拟合度R2与前人研究结果相比提高了10.3%[15,17]，均方根误差相比降低了52%[20]。但由于大气污染物形成机制的复杂性和多样性，模型精度存在一定误差。在针对不同区域和城市的PM2.5浓度分区模拟研究还有待进一步深入；另一方面，目前LUR建模主要以普通线性回归法进行模型构建，考虑的影响因子也通常集中在地形、人口、交通和土地利用类型等方面，这往往会对模型的精确度与解释能力造成负面影响。因此，改进LUR建模方法与扩展LUR模型的自变量也是当前的研究热点，未来可尝试利用神经网络、地理加权回归等方法改进模型，也可考虑将工业污染排放量、人均GDP等与经济相关的自变量因素加入模型，来提高模型的解释能力。

4.   结论

  • 1) 相关性分析结果表明，PM2.5浓度与耕地、林地、水体、草地、裸地、高程、降水量、相对湿度、风速和NDVI等呈负相关；与建设用地、气压、温度、人口密度、道路长度和污染源个数等呈正相关，其中高程与PM2.5浓度的相关系数最高。

    2) 利用LUR模型模拟了关中平原城市群各季节及年均的PM2.5浓度空间分布，模型调整后R2分别达到0.831 (春)、0.817 (夏)、0.874 (秋)、0.857 (冬)、0.900(全年平均)，模型拟合度较好。经精度检验，显示模型平均精度为80.4%，平均相对误差为12%，平均方根误差为7.37 μg·m−3。通过对比，年均LUR模型模拟效果最好。

    3) 模拟结果显示，研究区域各季节的PM2.5浓度空间分布呈现出东部高、西部低的明显特征，且其空间分布状况受地形因素的影响较大，浓度高值多集中在关中平原，低值多集中在秦岭山地。此外，各季节的浓度均值变化具有明显的差异性，具体表现为冬季最高、春秋次之、夏季最低。

    4) 运用在城市尺度PM2.5浓度模拟的LUR模型，也同样适用于中国西北部关中平原城市群类似的大区域尺度的PM2.5浓度空间分布模拟。经与实际状况相对比，LUR模型在模拟该区域PM2.5浓度时适用性好，精度高，解释能力强。通过模拟分析该研究区的PM2.5浓度空间分布特征，可为当地相关政府部门提供科学合理的PM2.5污染防治建议。

参考文献 (31)

返回顶部

目录

/

返回文章
返回

Copyright © 2019 中国科学院生态环境研究中心