-
1 数学模型
湍流流动是一种复杂三维非稳态的不规则运动,其脉动的大小和方向都是随机的。在湍流流动中,涡的叠加和分解都可以应用数学上的傅里叶变换来实现。大尺度涡主要由宏观流动以及边界条件决定,大尺度涡的尺度大于网格尺度,是产生低频脉动的主要原因;小尺度涡的尺度小于网格尺度,是产生高频脉动的主要原因。
-
1.1 大涡模拟控制方程
大涡模拟不可压缩流体的连续方程、动量方程和污染物扩散方
程[16] 分别为:式中:u为连续相速度,m·
s-1 ;up为速度,m·s-1 ;ν为分子黏性系数;D为分子扩散系数;Sc为污染物源项。假定过滤过程运算和求导运算可以交换,将N-S方程和对流扩散方程做过滤,得到如下方
程[17] : -
1.2 壁面模型
当颗粒和壁面发生碰撞的时候,阻尼力和弹性力共同施加在颗粒运动的法向上,分别为方程右边第2项和第1项,计算法向上受力的计算公式为:
式中:δn,ij为法向相对位移,m;knw,i为颗粒-壁面法向弹性系数;ηnw,i为阻尼系数;ni为颗粒i法向的单位矢量;vij为颗粒相对速度,m·
s-1 。在颗粒碰撞壁面的过程中,假设壁面为静止不动的,此时,颗粒相对速度为:
法向相对位移δn为:
类似于法向力的计算过程,颗粒-壁面碰撞的切向力Ftw,ij的计算公式为:
式中:δt,ij为切向的相对位移,m;ktw,i为颗粒碰撞壁面时的切向弹性系数;ηtw,i为阻尼系数。
-
2 计算模型建立及求解
-
2.1 计算模型建立及网格划分
根据DAVIDSON
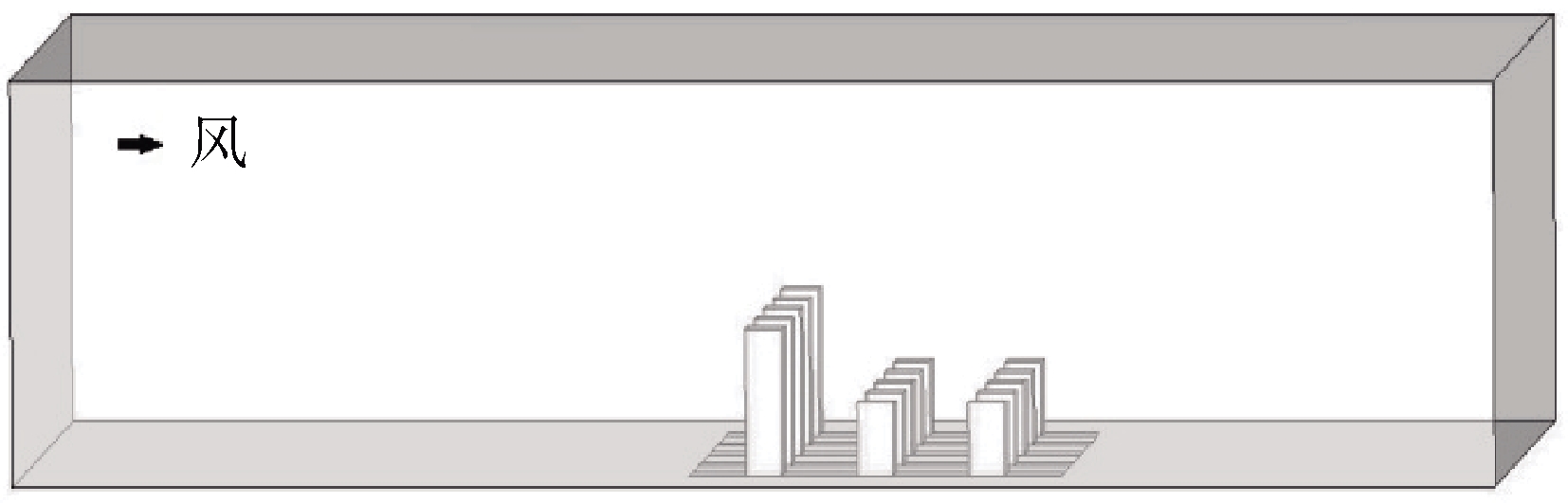
等[18] 的风洞实验所采用的阵列式构建建筑群模型,计算域的具体尺寸为:长400 m,宽200 m,高100 m;高建筑群的建筑模型长(W)、宽(D)和高(H)分别等于10、10和36 m,低建筑群的建筑模型长(W)、宽(D)和高(H)分别等于10、10和18 m,街道宽度(L)为20 m,建筑物空间位置关系和排放源位置如图1所示。通过网格无关性检验后,采用非结构化网格对计算域进行网格划分,划分时以建筑物表面作为源面,并对压力梯度较大的区域进行了网格加密,计算域网格数为2 691 912 个,其物理模型网格如图2所示。
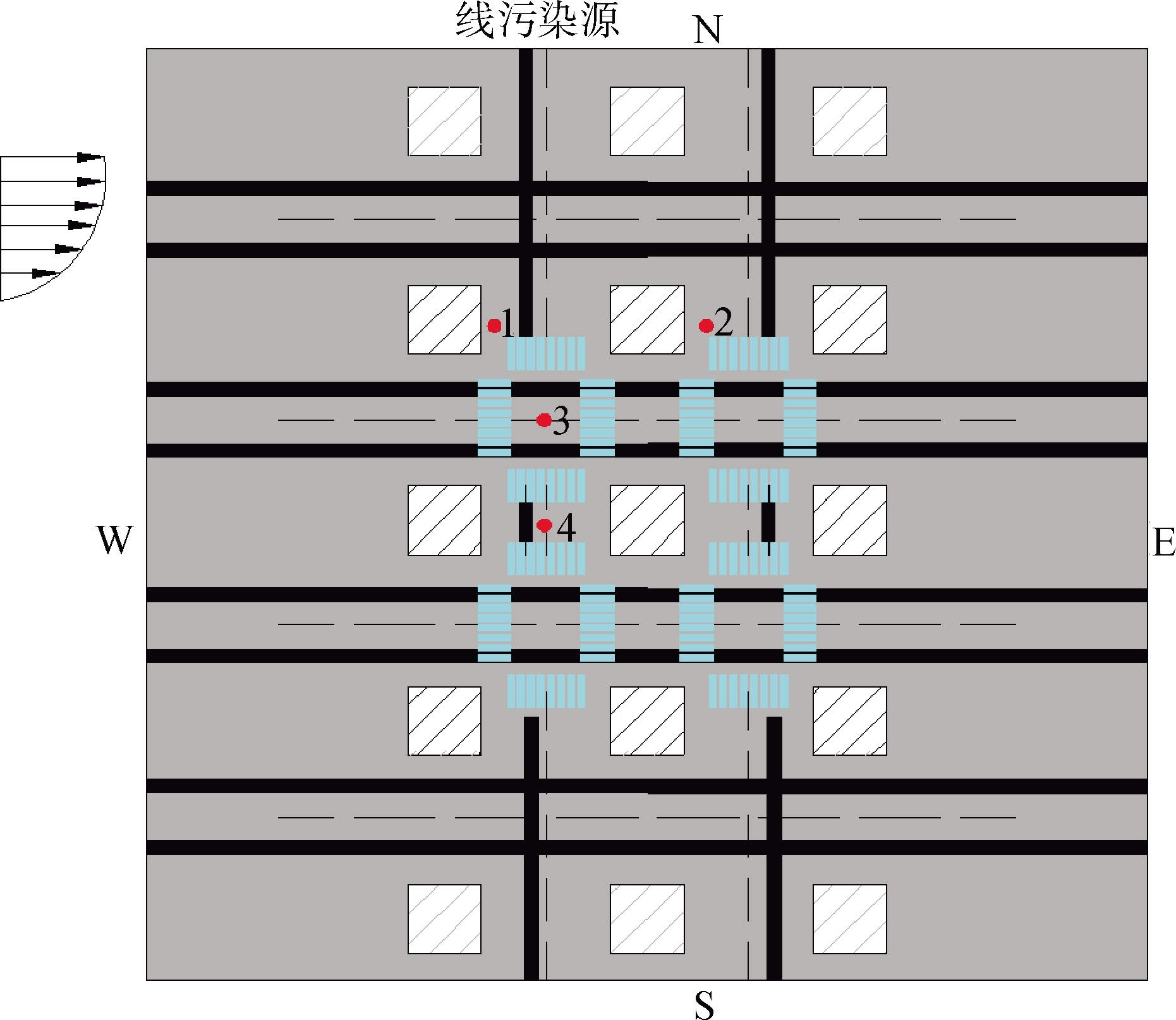
在建筑群附近和街道中间的行人呼吸带高度处(1.5 m高处)布置4个特征点,自西向东分别标记1~4,其空间坐标分别为(7,30,1.5)、(37,30,1.5)、(15,15,1.5)和(15,0,1.5);在背风面车道与迎风面车道分别布置线污染源,比较分析不同高度建筑群对监测点空气速度和颗粒物浓度的变化情况,其布置情况如图3所示。
-
2.2 边界条件设定及求解
通过使用用户自定义函数自定义一个抛物线形的入口速度,分布给速度进口,更好地反映实际情况。其速度边界条件采用幂函数形式的分布,表达式为:
建筑物壁面应用无滑移边界条件,出口边界为自由出口边界,计算域的两侧边界、上边界采用滑移边界,壁面粗糙度高度为0.4 mm,粗糙度常数为0.5。
颗粒物采用线源扩散模式,其质量流率为0.005 kg·
s-1 ,速度为0.5 m·s-1 ,粒径范围为0.1~10 μm,分布方式为R-R双峰分布,分布指数为 1.21,湍流扩散模型采用随机轨道模型,跟踪次数为500次,时间标尺为 0.15。 -
3 数值模拟结果及分析
-
3.1 城市街谷内气流场及颗粒物分布
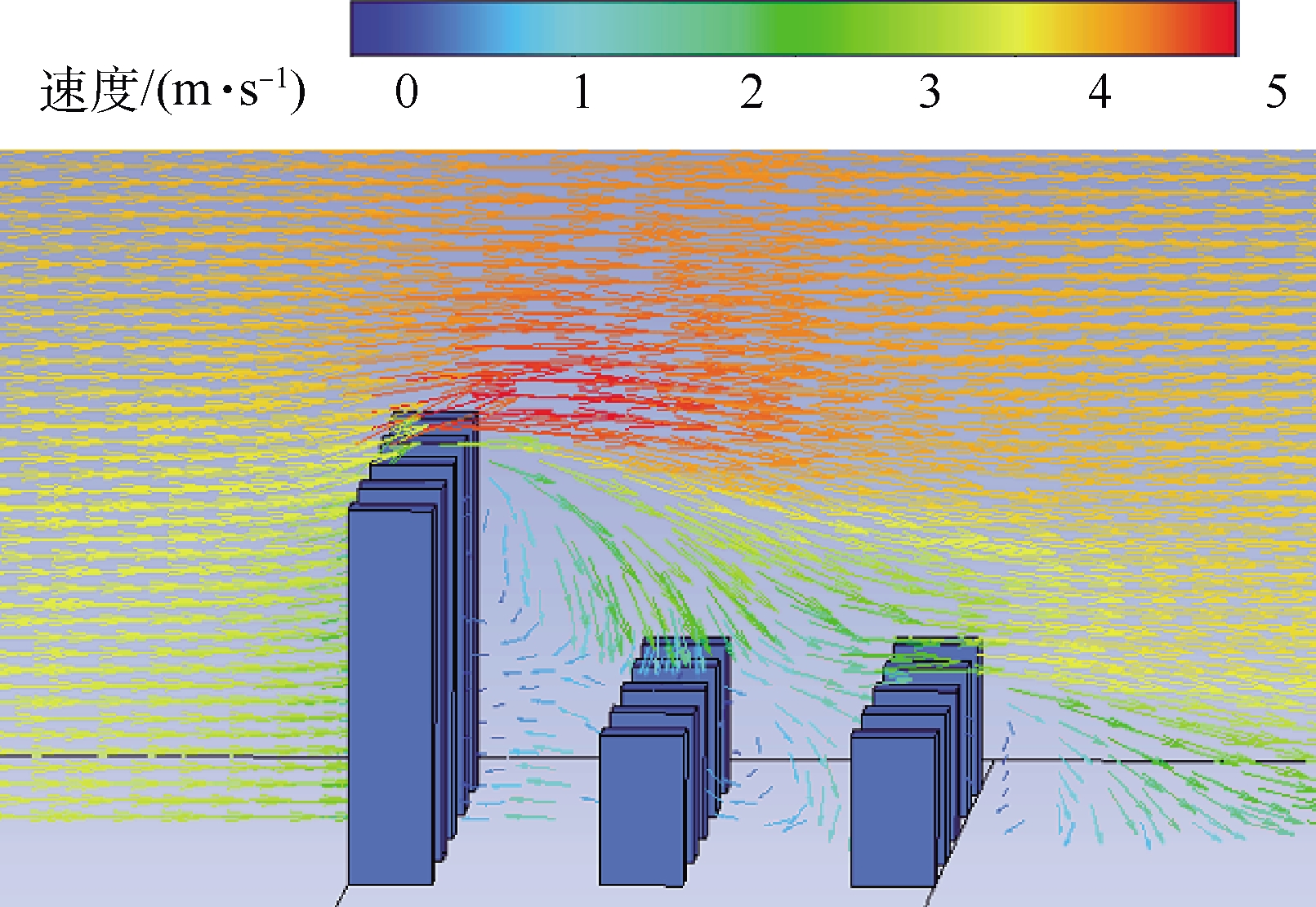
城市街谷内气流场和颗粒物分布情况是反映街谷内大气环境的基本信息,因此,模拟了前高后低型街谷内气流场速度大小、速度矢量图和颗粒物浓度及分布情况,如图4,5和图6所示。当风流吹向高层建筑物时,在其上端产生分流现象。由于城市峡谷存在高差,在高层建筑物上方形成一个顺时针旋涡,旋涡中心位于城市峡谷内靠近高层建筑群背风处,在这个顺时针旋涡的驱动作用下,在低层建筑群迎风墙角落形成了一个小的次生旋涡。由于风流在建筑群上方和街道内没有阻挡,在城市峡谷内迎风面的风速较大,风流风速最大值达到5.0 m·
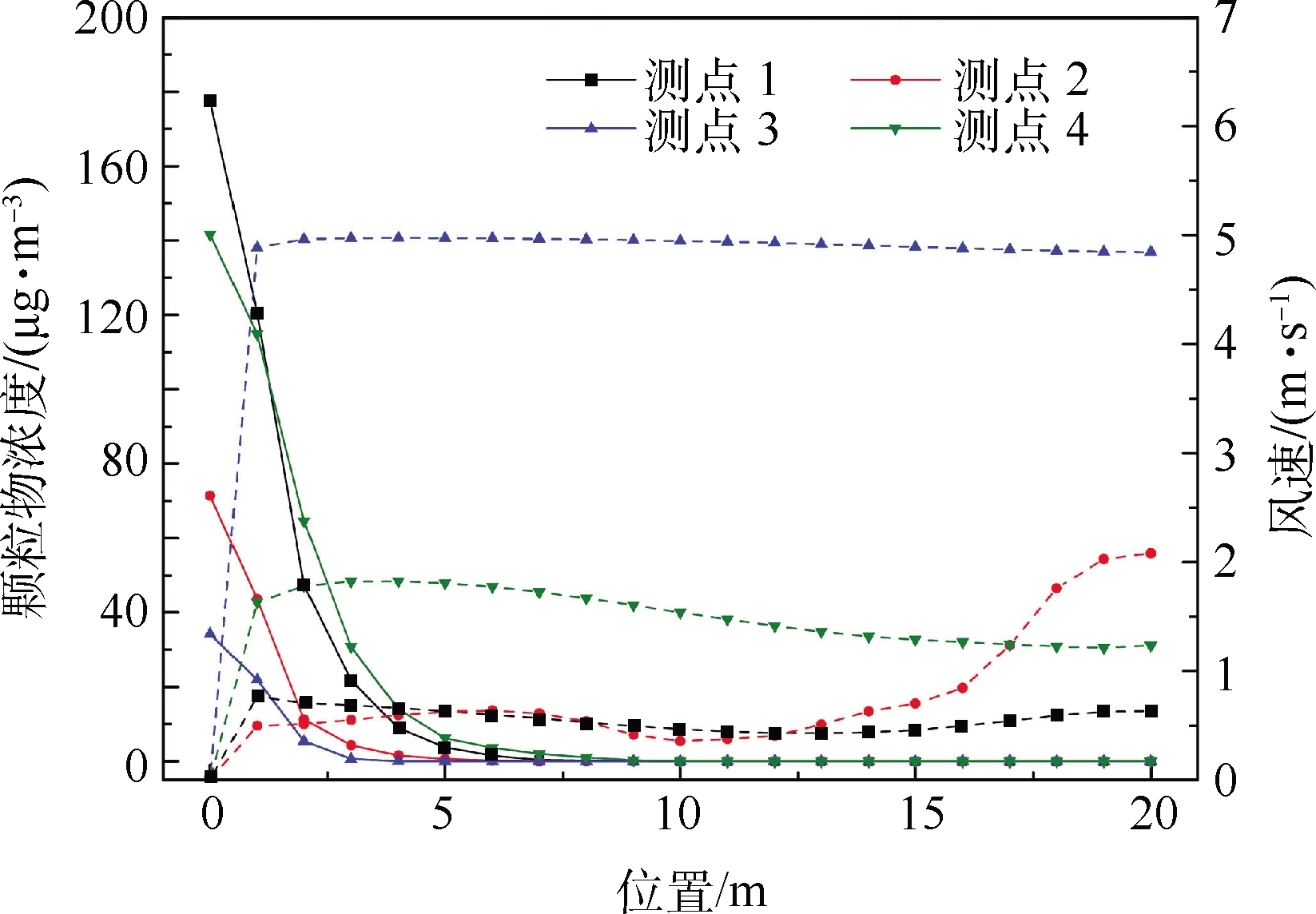
s-1 ,但在涡旋作用下,城市峡谷内气流流动性减弱,风流风速最小值达到0.7 m·s-1 。将4个监测点在垂直方向20 m不同位置的风速和颗粒物浓度XY散点数据导出,如图7所示。在顺时针旋涡的作用下,大量可吸入颗粒物积聚在高层建筑群背风侧,导致低建筑物迎风侧的可吸入颗粒物浓度高于背风侧,其浓度最大值达到495 μg·
m-3 。 -
3.2 街谷形状因子对气-固流场的影响
高层建筑群与低建筑群形成的街谷内空气流动形态跟街谷几何特征参数密切相关,故此处提出街谷形状因子的计算公式,其表达式为:
式中:λ为街谷形状因子;H为高层建筑群高度,m;Hd为相邻低层建筑群高度,m。
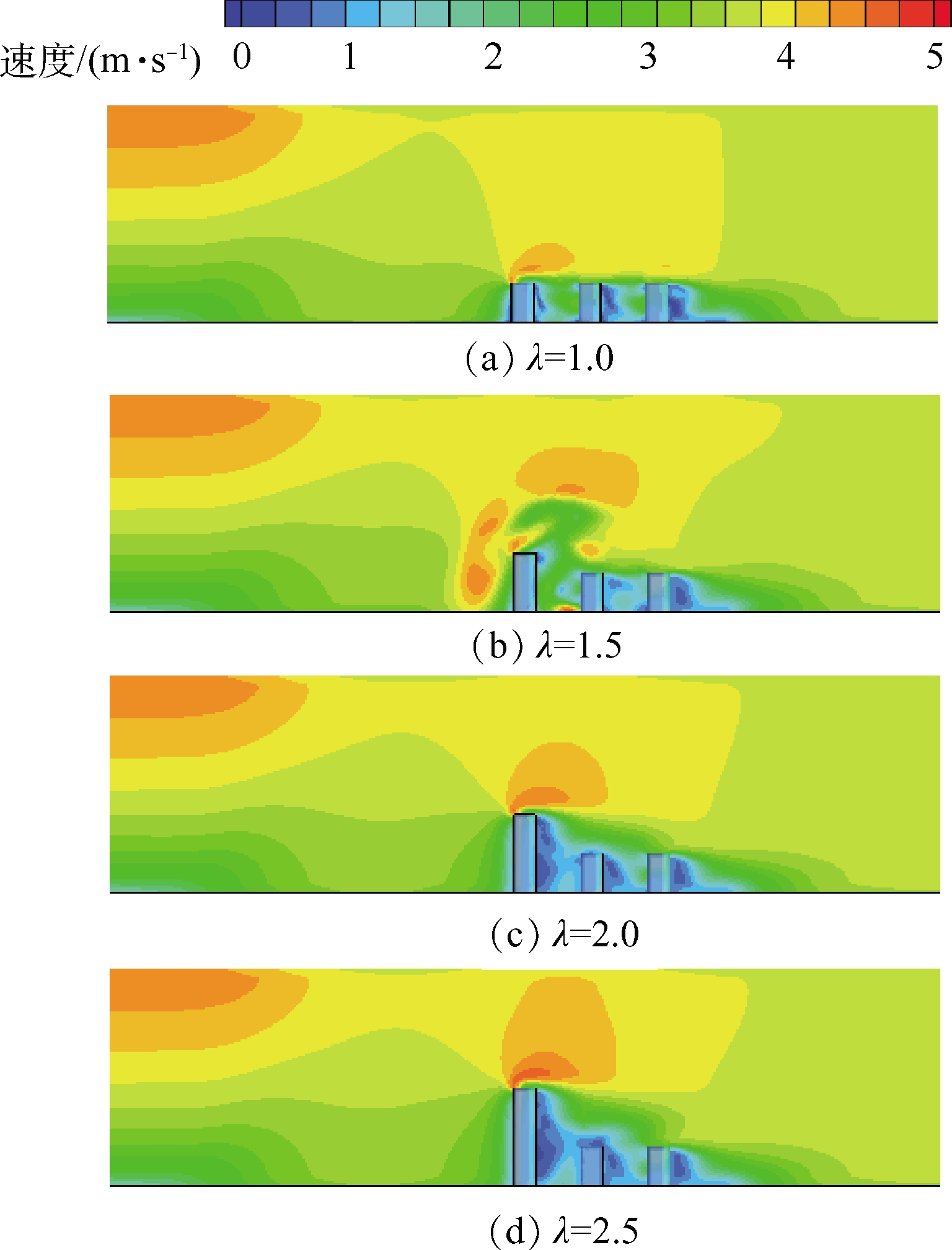
为了研究街谷形状因子对颗粒物扩散的影响,在相同街道宽情况下,对街谷形状因子分别为1.0、1.5、2.0和2.5时的气流场和颗粒物浓度场进行模拟,其模拟结果如图8,9,10所示。随着街谷形状因子的增大,高层建筑物上方的剪切层湍动能亦相应增强。当λ=2.5时,湍动能为1.9
m2 ·s-2 ,同时,顶端下沉气流逐渐减小。此时,城市峡谷内的顺时针旋涡逐渐增大,导致城市峡谷内空气流动性减弱,其风速逐渐减小至0.25 m·s-1 。随着街道峡谷深度的增加,峡谷内旋涡的空气流动性减弱,大量可吸入颗粒物被积聚在高层建筑背风侧底部,导致高层建筑底部和该侧人行道可吸入颗粒物浓度增大。当λ=2.5时,高层建筑群底部颗粒物浓度达到605 μg·m-3 。 -
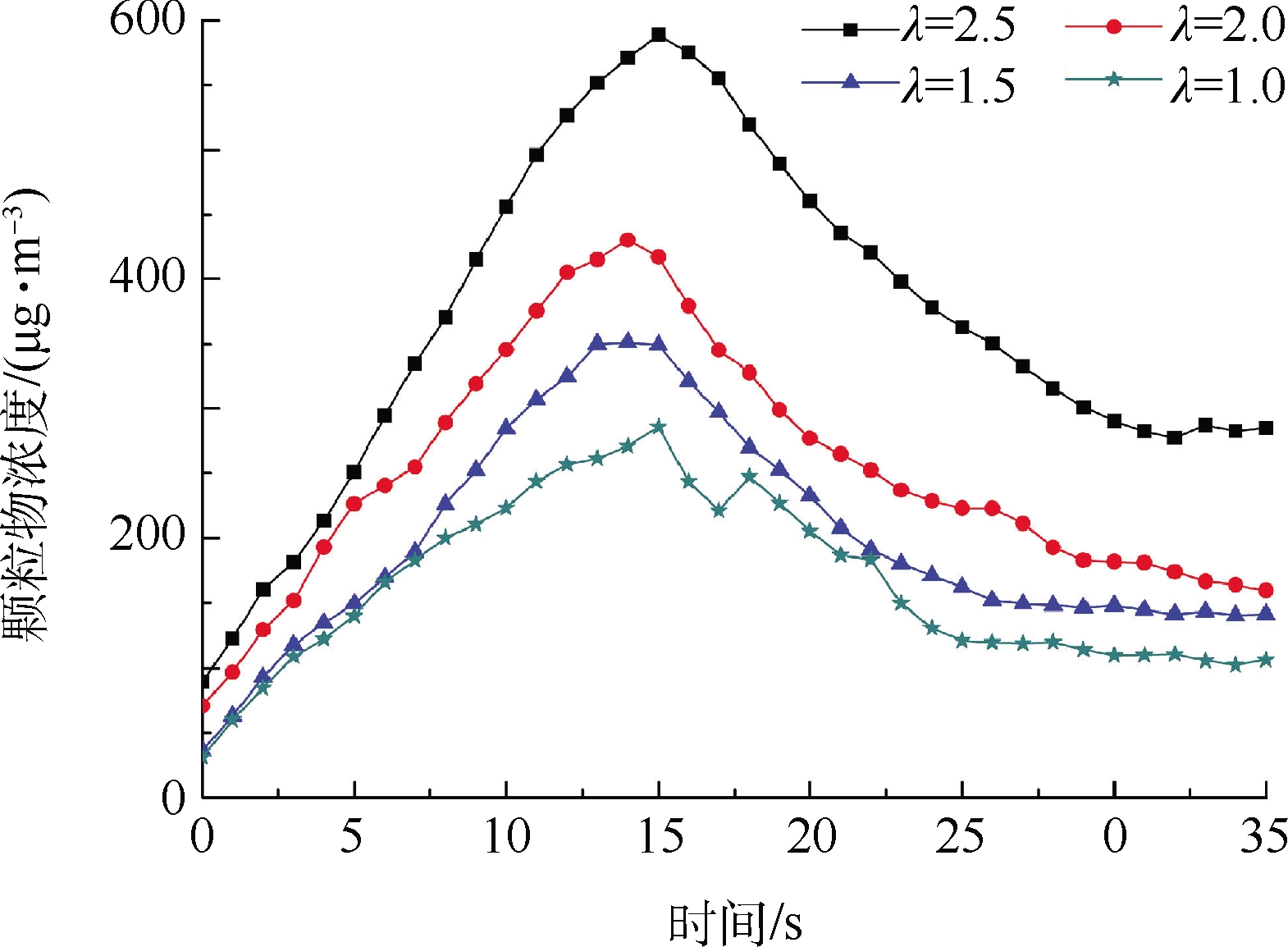
3.3 街谷形状因子对可吸入颗粒物浓度影响
监测点1和监测点2的颗粒物浓度随监测时间变化情况如图11和图12所示。在街谷形状因子保持不变的情况下,同一街谷监测点1可吸入颗粒物浓度比监测点2高,这是由于在涡旋和气流夹带作用下,空气流动性差,不利于污染物扩散,大量可吸入颗粒物聚集于高层建筑群背风侧;高层建筑群的滞留效应,导致城市街谷内可吸入颗粒物的稀释扩散条件变差,不利于可吸入颗粒物向城市峡谷上部空间扩散,可吸入颗粒物浓度在垂直方向上的分布具有明显的分层现象。
-
4 结论
1) 随着街谷形状因子的增大,高层建筑物上方剪切层湍动能相应增强,城市峡谷内顺时针旋涡随之逐渐增大,导致城市峡谷内空气流动性减弱,其风速逐渐减小至0.25 m·
s-1 。2) 随着街道峡谷深度的增加,峡谷内旋涡的空气流动性相应减弱,大量可吸入颗粒物被夹带到高层建筑背风侧底部,导致高层建筑底部和该侧人行道可吸入颗粒物浓度增高达到605 μg·
m-3 。3) 高层建筑群的滞留效应,导致城市街谷内可吸入颗粒物的稀释扩散条件变差,可吸入颗粒物浓度在垂直方向上的分布具有明显的分层现象。
-
参 考 文 献
-
1
顾兆林, 张云伟. 城市街谷的空气流动与污染物扩散研究: 物理模型的发展及数学模拟[J]. 地球环境学报, 2011, 2(2): 362-373.
-
2
冯寒立, 赵敬德, 翟静. 高架覆盖的街谷内可吸入颗粒物的浓度分布[J]. 环境工程学报, 2017, 11(8): 4669-4676.
-
3
白志鹏, 张文杰, 韩斌, 等. 我国环境空气颗粒物质量基准研究框架及研究体系的构建[J]. 环境科学研究, 2015, 28(5):667-675.
-
4
DONG J, TAN Z, XIAO Y, et al. Seasonal changing effect on airflow and pollutant dispersion characteristics in urban street canyons[J]. Atmosphere, 2017, 8(43): 1-18.
-
5
张传福, 曾建荣, 文谋, 等. 高架桥对街道峡谷内大气颗粒物输运的影响[J]. 环境科学研究, 2012, 25(2): 159-164.
-
6
JICHA M, KATOLICKY J, POSPISIL J. Dispersion of pollutants in a street canyon and street intersection under traffic-induced flow and turbulence using a low Re k-ε model[J]. International Journal of Environment and Pollution, 2002, 18(2): 160-170.
-
7
XIE X M, HUANG Z, WANG J S. Impact of building configuration on air quality in street canyon[J]. Atmospheric Environment, 2005, 39(25): 4519-4530.
-
8
XIE X M, HUANG Z, WANG J S, et al. The impact of solar radiation and street layout on pollutant dispersion in street canyon[J]. Building and Environment, 2005, 40(2): 201-212.
-
9
RAMAMURTHY P, PARDYJAK E R, KLEWICKI J C. Observations of the effects of atmospheric stability on turbulence statistics deep within an urban street canyon[J]. Journal of Applied Meteorology & Climatology, 2007, 46(12): 2074-2085.
-
10
GU Z L, ZHANG Y W, CHENG Y, et al. Effect of uneven building layout on air flow and pollutant dispersion in non-uniform street canyons[J]. Building & Environment, 2011, 46(12): 2657-2665.
-
11
WANG L, PAN Q, ZHENG X P, et al. Effects of low boundary walls under dynamic inflow on flow field and pollutant dispersion in an idealized street canyon[J]. Atmospheric Pollution Research, 2017, 8(3): 564-575.
-
12
MARCOS M Á P, FEIJÓ-MUŃOZ J, MEISS A. Wind velocity effects on the quality and efficiency of ventilation in the modeling of outdoor spaces: Case studies[J]. Building Services Engineering Research & Technology, 2015, 37(1): 2661-2665.
-
13
MOCHIDA A, TOMINAGA, YOSHIHIDE, et al. Comparison of various k-ε models and DSM applied to flow around a high-rise building: Report on AIJ cooperative project for CFD prediction of wind environment[J]. Wind and Structures, 2002, 5(2/3/4): 227-244.
-
14
张云伟, 王晴茹, 陈嘉, 等. 城市街谷内PM2.5浓度时空变化及影响因素分析[J]. 中国环境科学, 2016, 36(10): 2944-2949.
-
15
陈晓萌, 亢燕铭, 杨方, 等. 上游阻挡建筑间距对街谷内空气环境的影响[J]. 中国环境科学, 2016, 36(7): 1967-1973.
-
16
陈巨辉. 基于大涡模拟: 颗粒二阶矩的两相流动与反应数值模拟[D]. 哈尔滨: 哈尔滨工业大学, 2013.
-
17
赵宝芹, 王嘉松, 汪立敏, 等. 城市对称街道峡谷气流及污染物扩散特征的研究[J]. 水动力学研究与进展, 2005, 20(5): 610-615.
-
18
DAVIDSON M J, MYLNE K R, JONES C D, et al. Plume dispersion through large groups of obstacles: A field investigation[J]. Atmospheric Environment, 1995, 29(22): 3245-3256.
-
1
全文HTML
摘要
为了获得城市冠层内高层建筑群的高度变化对城市颗粒物污染的作用情况,采用大涡模拟方法研究了不同高层建筑群的街谷形状因子对街谷内空气流动与污染物扩散规律的影响。结果表明:在高层建筑群上方形成一个顺时针旋涡,旋涡中心位于城市峡谷内靠近高层建筑群背风处;随着街谷形状因子的增大,高层建筑群的滞留效应增强,导致高层建筑物上方的剪切层湍动能增强;当形状因子为2.5时,湍动能达到1.9
Abstract
In order to obtain the effects of height variation of high-rise buildings in urban canopy on the particulate pollution, large-eddy simulation was used to study the influence of street shape factors of different high-rise buildings on airflow and pollutant diffusion in the canyon. The simulation result shows that a clockwise vortex could be formed above the high-rise buildings, and its center is located near the lee of the high-rise buildings in the urban canyon. With the increase of the shape factor of the valley, the particulate-retention effect of the high-rise buildings will increase, which could strengthen the turbulent kinetic energy and air stagnation of the shear layer above the building. The dilution and diffusion conditions of the inhalable particles in the urban street canyon become worse at the shape factor of 2.5 and the turbulent kinetic energy is 1.9
城市人居环境是以人为中心,由建筑-道路-生态环境构成的综合
然而,真实街谷内的流场流动是一种复杂三维非稳态的不规则湍流运动,湍流脉动的大小和方向都是随机的。同时,城市峡谷内空气污染治理是一个涉及环境与城市规划等多学科的技术难题。鉴于此,采用大涡模拟方法分析高层建筑群的街谷形状因子对街谷内空气流动与污染物扩散的影响规律,为防治颗粒污染物在城市区域的累积提供参考。

图9 不同街谷形状因子下Y=0 m平面湍动能分布
Fig.9 Simulation result of turbulence kinetic energy under different street shape factors in Y=0 m plane
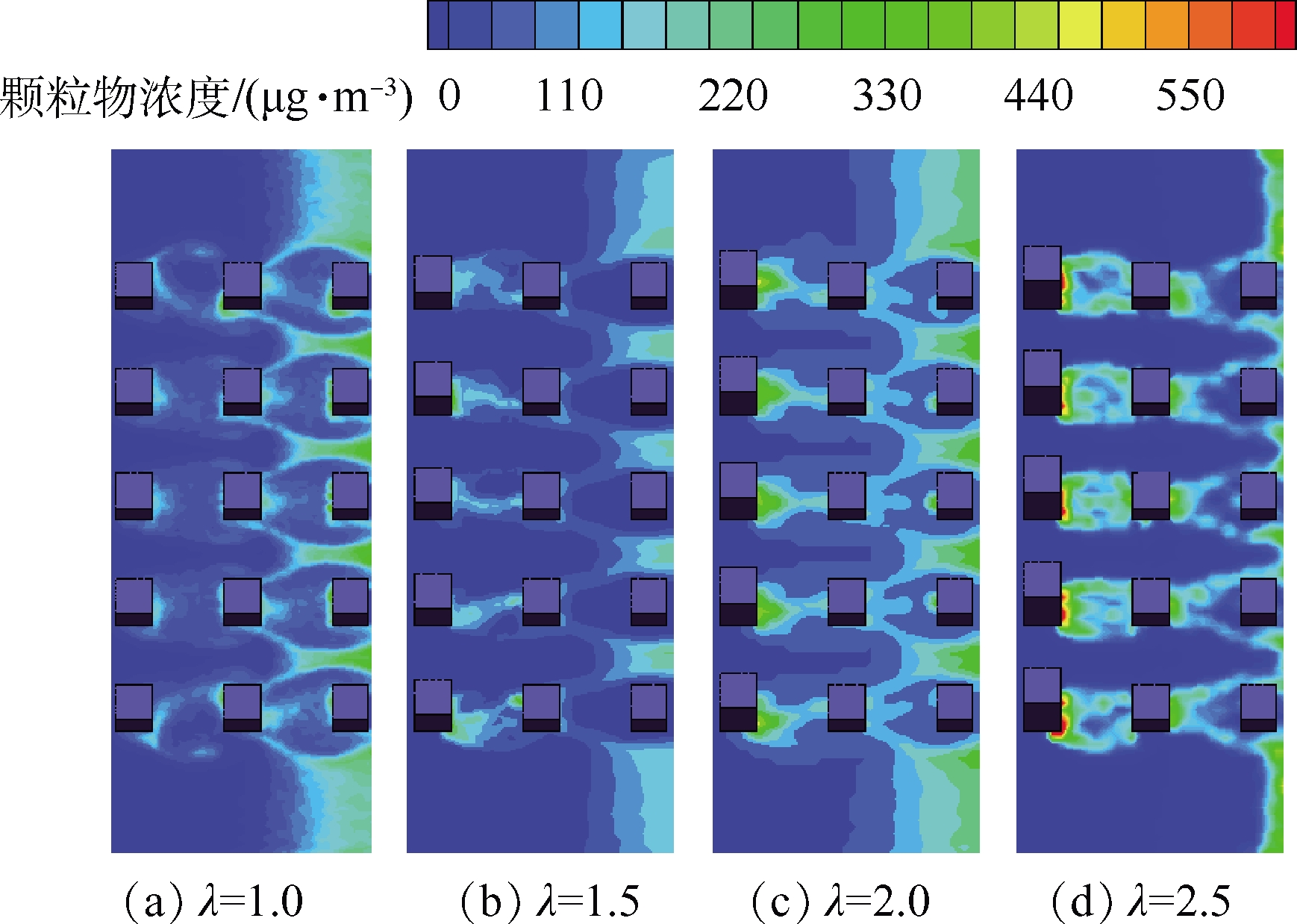
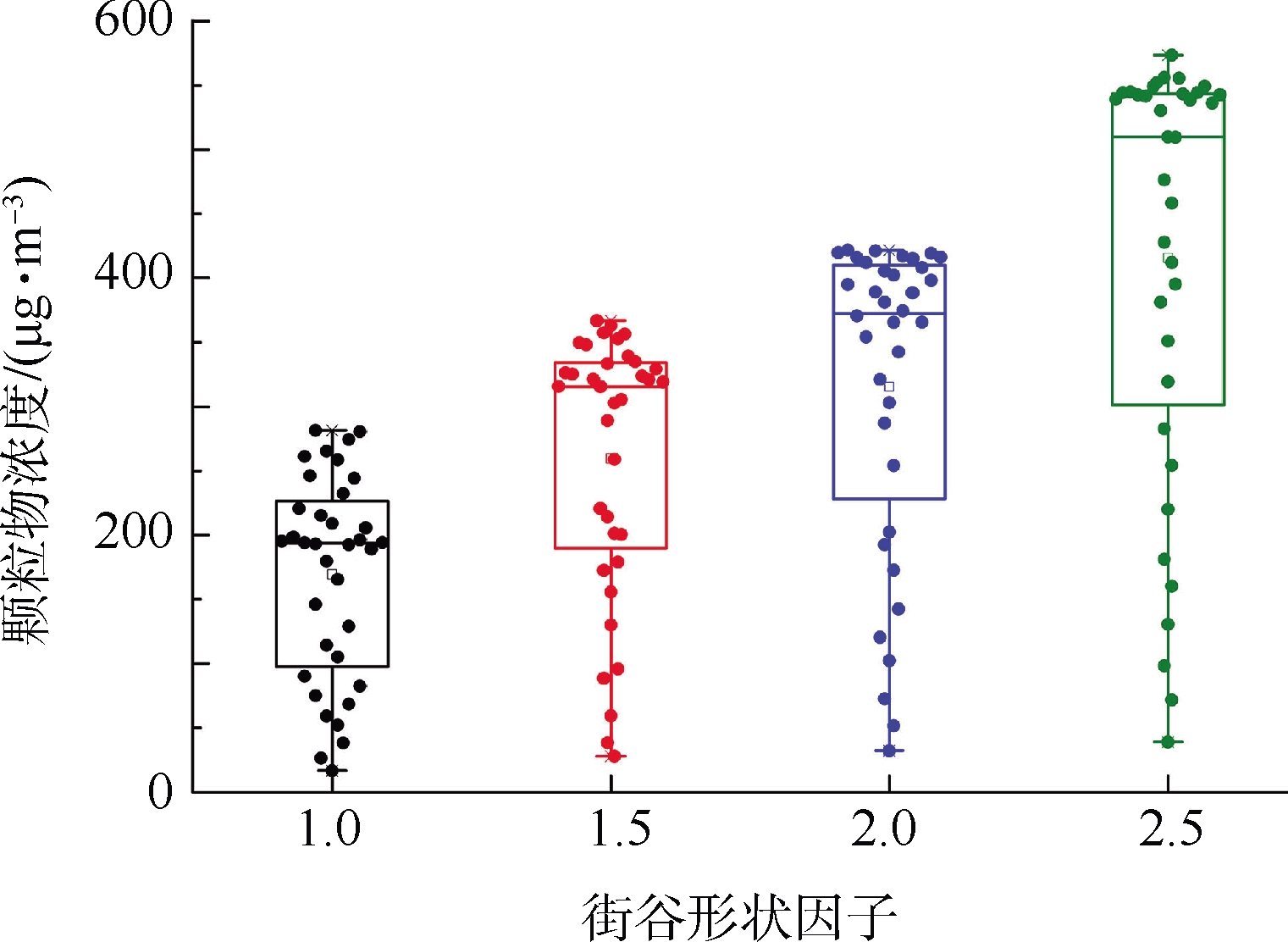
图10 不同街谷形状因子下Z=1.5 m平面细颗粒物浓度
Fig.10 Simulation result of particulate concentration under different street shape factors in Z=1.5 m plane








 百度学术
百度学术


 下载:
下载:
