工业园区大气污染排放总量核算为园区大气环境质量管控提供重要依据，同时有助于推进企业排污许可、项目审批、执法监管以及排污权交易等管理联动，与排污总量挂钩，有助于提升综合管理效能、制定相关的环境管理政策^[1]和解决污染源管控不准、产业调整方向不明、环评审批总量落实难、第三方机构弄虚作假等问题具有重要意义^[2-3]。目前，工业园区大气污染物排放总量的核算主要是统计园区内所有企业大气污染物排放量并进行加和代表该园区大气污染物的排放总量。现有对企业排放量核算方法主要有实测法、产排污系数法及物料衡算法。实测法是依据实际监测环统对象产生和外排废气流量及其污染物质量浓度，计算出废气的排放量及各种污染物的产生量和排放量 (在线监测和手工监测) ^[4]。产排污系数法是根据《产排污系数手册》^[5]提供的工业行业产排污系数，只要根据企业的实际情况选择合适的产排污系数，即可核算出污染物的产生量和排放量^[6]。物料衡算法是通过计算生产过程中物质的量的变化对生产过程中使用的物料变化情况进行定量分析的一种方法^[7]。但上述通过对企业排放量核算园区总排放量的方法均存在一定的局限性，如实测法 (在线监测和手工监测) 存在设备安装联网成本较高，运维困难、无法测算无组织排放等问题且监控数据无法验证^[8-9]。产排污系数法忽视了企业生产过程中采取不同污染处理技术的因素，在计算过程中仅以企业生产消耗的原材料或生产成品就确定了一个企业的排放系数，未考虑企业对于污染管理和处理技术方面的因素，具有一定的局限性^[6]。产排污系数法对于关键系数的选取存在一定主观性且可能会忽略行业特征^[5]。而物料衡算法计算过程复杂，生产过程中的物料损耗、污染物的无组织排放等因素无法准确估算，适用范围较小等^[4,10]。与此同时，产排污系数法和物料衡算法通常需要对生产企业进行调研，对于企业数量和类型较多的工业园区，核算的人力成本和时间成本较高，难以实现动态核算更新。

本研究尝试探索基于环境监测站点的实时监测数据，结合大气污染物扩散模型和源参数反演算法，构建工业园区大气污染物实际排放总量反演算法，实现对园区无组织及低矮有组织大气污染物实际排放量的动态实时核算。该方法可极大地节省人力、物力，具有普遍适用性。该方法可作为实测法、物料衡算法及产排污系数法等传统排放总量核算方法的有益补充，同时有助于充分利用环境监测数据信息，明确环境质量与污染物排放的动态响应关系，为基于环境质量目标的动态污染排放管控提供参考。

1.   研究方法

1.1   示例园区基本情况及模拟网格构建

示例园区为东南沿海某重点石油化工产业基地，是国家石化产业布局方案中重点规划布局的新建石化产业基地。2021年，依据江苏省开展工业园区 (集中区) 污染物排放限值限量管理工作方案要求^[2]，建设了园区大气环境监测站点网络，并对园区企业大气污染排放情况进行了调查核算。该园区内共有涉及有机化学品的合成、储运、化学加工制造、危废治理、热电联产等污染排放企业20家。其生产及排放规模排名前10的企业VOCs排放总量占园区VOCs总排放量超过95%。因此，选取该10家企业作为主要研究对象，以VOCs的实际排放量实时反演为主要研究目标。由于本研究主要论证基于大气环境监测数据的污染排放总量实时反演的技术可行性，并讨论相关影响因素，故不考虑在工业园区尺度范围内VOCs的二次转化。

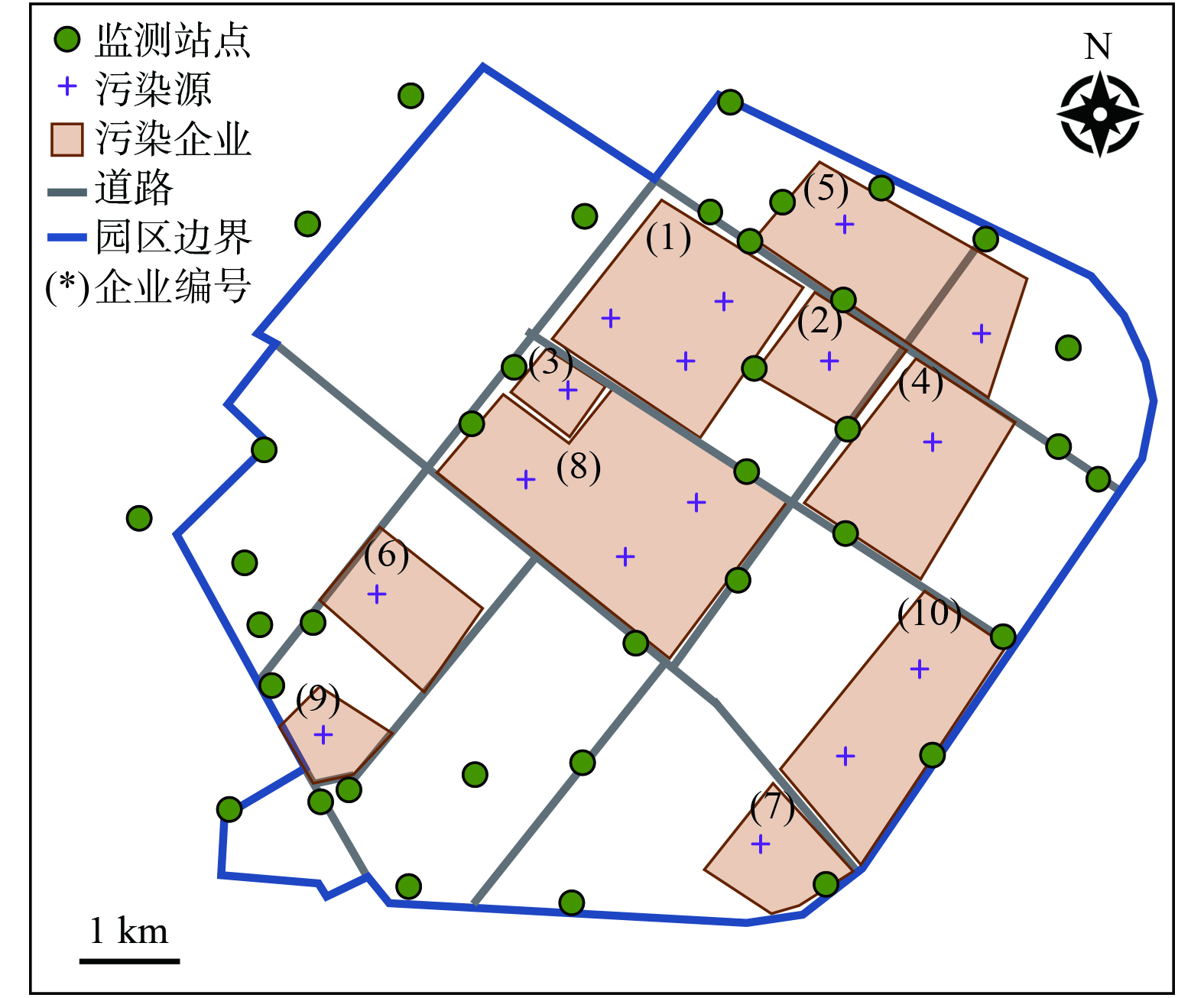
将园区在WGS-84地理坐标系下的企业排污单元及监测站点经纬度、园区边界及主要道路矢量图信息转化为UTM投影坐标系以方便进行数值模拟。图1为园区主要污染企业、监测站点、园区边界及主要道路的空间分布情况。

图 1  示例园区污染源及监测站点布局图

Figure 1.  Layout of pollution sources and monitoring stations in sample park

下载: 全尺寸图片 幻灯片

选取园区几何中心作为原点，计算各排污单元及监测站点的相对空间位置。表1为污染排放占比前10企业各污染排放点位的相对位置、排污许可中VOCs的年排放量 (许可排放量) ，以及通过在线监测、产能折算、产排污系数、物料衡算等方式核算的VOCs年排放量 (统计核算量) 。核算年度为2020年，部分企业如企业 (8) 、企业 (10) 在核算年度尚未正式投产，故其统计核算量处于缺失状态。在本研究过程中，相关企业已正式投产，故在模型模拟中将参考许可排放量作为污染源，考虑其排放过程对周边环境的影响。经统计，示例园区VOCs年排污许可量约为4 000 t。

表 1  示例园区污染源相对位置及VOCs年排放量

Table 1.  Relative location of pollution sources and annual emissions of VOCs in sample park

企业编号	点位编号	相对位置			VOCs年排放量
		X/m	Y/m		许可排放量/(t·a−1)	统计核算量/(t·a−1)
(1)	1-1	−105.69	1 939.64		558.06	305.68
	1-2	694.15	1 513.34
	1-3	1 080.49	2 126.93
(2)	2-1	2 191.57	1 535.64		231.22	52.70
(3)	3-1	−567.09	1 159.14		0.00	0.00
(4)	4-1	3 307.64	732.23		257.24	2.46
(5)	5-1	2 328.21	2 950.21		188.13	11.10
	5-2	3 805.85	1 865.68
(6)	6-1	−2 494.02	−1 017.60		16.17	0.84
(7)	7-1	1 605.90	−3 561.35		1.01	0.46
(8)	8-1	−945.73	223.88		1 855.47	—
	8-2	100.86	−572.14
	8-3	842.90	27.32
(9)	9-1	−3 033.36	−2 506.92		23.64	0.14
(10)	10-1	2 488.31	−2 613.47		801.12	—
	10-2	3 236.00	−1 661.56

 | Show Table

DownLoad: CSV

1.2   环境监测数据处理

本研究基于工业园区地面监测站点实时监测数据开展大气扩散模拟。其中，模型采用的平均风场数据为园区内各监测站点小时平均风向的平均值，计算式见式 (1) 和式 (2) 。

式中：$u$、$v$分别为风向在纬线方向和经线方向的分量；${w}_{s}$是风速，m∙s⁻¹；$\theta$为以北风为0^o的风向角度。

式中：${u}_{m}$、${v}_{m}$分别为平均风向量在纬线方向和经线方向的分量；$N$为监测站点总数；${u}_{i}$、${v}_{i}$分别为监测站点i的小时监测分量。

1.3   高斯烟羽大气污染扩散模型

高斯烟羽大气污染扩散模型是基于随机扩散形成高斯分布的污染物浓度场理想假设的第一代空气质量模型，适用于平坦地形下稳态风向中污染物的扩散模拟。随着研究的深入，进一步推出了第二代空气质量模式如AERMOD^[11]、CALPUFF^[12]和第三代空气质量模式如CMAQ^[13]，考虑了更为复杂的影响大气污染物扩散及二次转化的因素。然而，由于其快速简单的特点，高斯模型仍在应急处置、污染初步估算等领域被广泛应用^[14]。本研究主要讨论基于环境监测站点监测数据开展工业园区大气污染排放总量实时反演的技术可行性，为简化起见，采用高斯烟羽大气污染扩散模型对该方案进行测试。在实际使用中，其他空气质量模型也可类似地应用于工业园区总量核算中。

高斯烟羽大气污染扩散模型的解析形式见式 (3) 。

式中：${Q}_{0}$为污染源的排放强度，mg∙s⁻¹；$U$为平均风速，m∙s⁻¹；${\sigma }_{y}$、${\sigma }_{z}$分别为横向和纵向的扩散参数，该参数的值是$x$的函数，m；$C\left(x,y,z\right)$为质量浓度关于三维空间位置的分布函数，mg∙m⁻³；${y}_{0}$、${z}_{0}$分别为污染源的空间位置。此处，$x$是横向垂直于平均风向的方向，y是横向平行于平均风向的方向，z是纵向垂直于风场平面的方向。

定义$\alpha$为污染源对任意点位的污染物浓度贡献比率计算式为式 (4) ，则排放强度为${Q}_{0}$的污染源对任意点位的污染浓度贡献可由${Q}_{0}\cdot \alpha$得到，${\sigma }_{y}$、${\sigma }_{z}$的计算是高斯烟羽扩散模型应用的关键。

本研究参考国标参数化方案《制定地方大气污染物排放标准的技术方法》 (GB/T 3840-91) ^[15]逐小时实时计算${\sigma }_{y}$、${\sigma }_{z}$的数值。具体见式 (5) 。

式中：参数${\gamma }_{1}$、${\gamma }_{2}$和${\alpha }_{1}$、${\alpha }_{2}$具体取值与大气稳定度等级有关，大气稳定度等级可根据太阳倾角、云量、风速等气象信息估算获得。具体估算方法及参数取值参照标准GB/T 3840-91^[5]。

1.4   优化函数构建及源参数反演算法

监测站点污染物的监测质量浓度为背景质量浓度、污染源贡献质量浓度和监测误差累加而成。假设园区存在监测站点N个，污染源M个，则对于任意监测站点i，有监测污染物质量浓度${d}_{i}$为式 (6) 。

式中：$bg$为背景浓度。假设在工业园区尺度范围内，污染物的背景质量浓度是均一的常数，${\varepsilon}_{i}$为监测站点i对目标污染物的监测误差，其计算式为式 (7) 。

式中：$\varepsilon$为控制监测误差强度的系数，$\chi$为均值为0，方差为1的高斯分布。

以此构造优化目标函数见式 (8) 。

式中：$\widehat{bg}$、${\widehat{Q}}_{j}$分别为背景浓度和污染源j排放强度的估算值。该值将在优化目标函数的迭代过程中被不断优化，直到趋近于实际情况。$a$、$b$为目标函数的一阶和二阶正则项系数，该系数取值可通过贝叶斯优化获得。基于前人研究，对源参数反演的优化算法选取有较多讨论，如采用Nelder-Mead优化法^[16]、粒子群算法 (PSO) ^[17]、遗传算法 (GA) ^[18-19]等。为验证基于环境监测站点开展工业园区大气污染物实际排放总量实时核算的可行性，本文采用基础的Nelder-Mead算法作为优化器。在实际使用中，可根据实际情况采用其他优化算法。

1.5   误差分析

本研究主要采用平均绝对相对偏差 (Mean Absolute Relative Error， MARE) 作为排放总量反演误差的度量，其计算公式见式 (9) 。

式中：T为核算时段的小时数；${\widehat{x}}_{n}$，${x}_{n}$分别为反演排放量和模拟排放量；$\left|\cdot \right|$表示绝对值。

2.   结果与讨论

2.1   数值模拟与排放总量反演

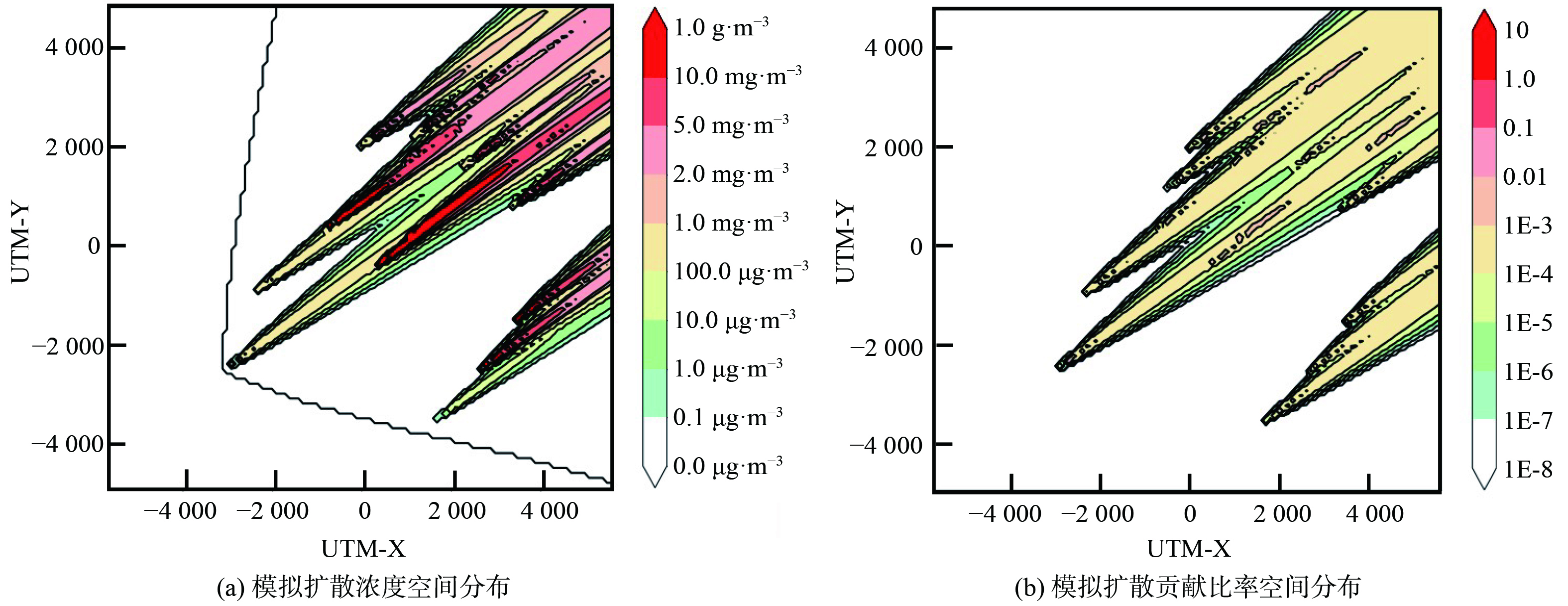
收集园区2023年1月1日0时至1月31日23时地面气象监测数据开展模拟研究。参考表1中收集的企业许可排放量数据设定模拟的污染源排放强度。其中，大型企业生产单元占地面积较大，存在多个排放点位 (如企业1) ，则将企业的年排放量均匀分配到每个排放点位。将各个点位的排放强度由t∙a⁻¹转化为mg∙s⁻¹带入公式 (3) 中，获取各污染源对监测点位贡献C，背景浓度设定为0~0.3 mg∙m⁻³的随机数。依照公式 (5) 可获得园区监测点位的监测浓度值${d}_{i}$。

为验证基于环境监测数据对工业园区排放总量进行实时反演核算的有效性和适用性，研究设定了4个不同排放情景：高排放情景、中排放情景、低排放情景和周期排放情景。其中，高、中、低排放情景分别为实际排放量占许可排放量的100%、50%和10%，周期排放情景则设定园区排放以24 h为周期依照正弦函数在许可排放量的20%~120%内波动。图2展示了高排放情境下，园区2023年1月1日00时污染物质量浓度及污染源对监测点位贡献比率的空间分布情况。

图 2  示例园区2023年1月1日00时模拟扩散浓度及贡献比率空间分布

Figure 2.  Simulated diffusion concentration (left) and contribution ratio (right) spatial distribution at 00:00 on January 1, 2023 of sample park

下载: 全尺寸图片 幻灯片

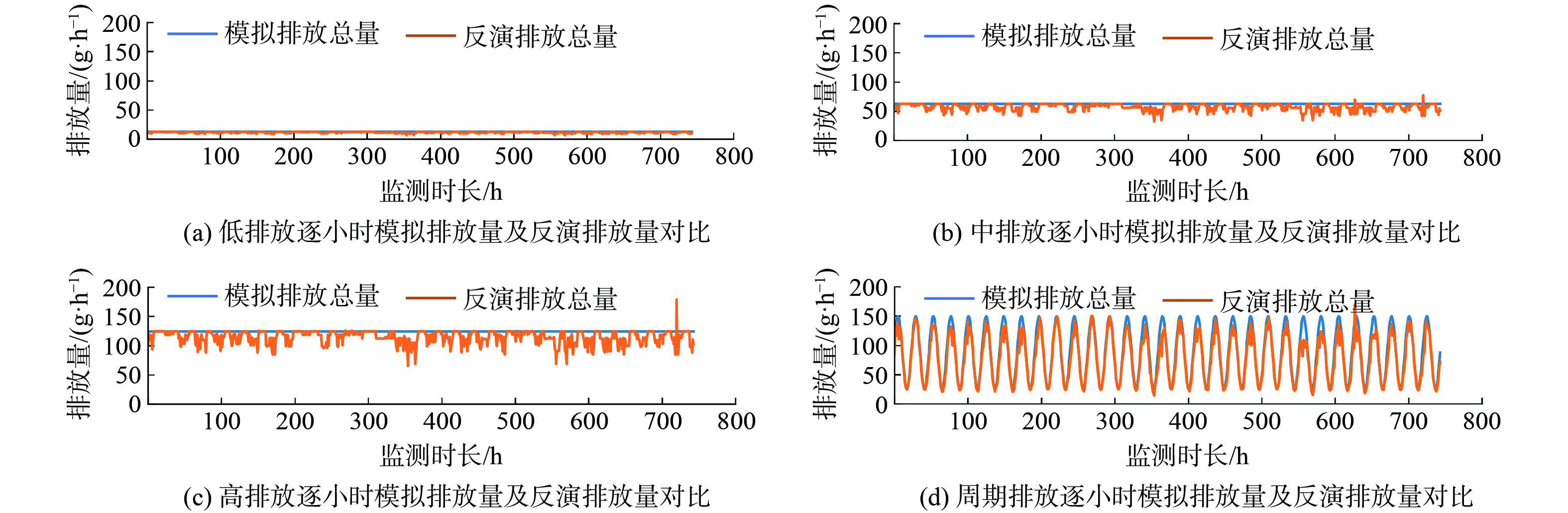
利用模拟的在线监测浓度值，以公式 (7) 为目标函数 (设定正则项为0) ，进行反演核算。图3展示了4种排放情景下逐小时的模拟排放量和反演排放量。结果表明，在该条件下模拟排放量逐小时变化曲线与模拟排放量的逐小时变化曲线基本一致，部分时刻存在明显偏差。

图 3  不同排放情景下逐小时模拟排放量及反演排放量对比

Figure 3.  Comparison of hourly simulated emissions and inverted emissions under different scenarios

下载: 全尺寸图片 幻灯片

计算1月份逐小时反演排放总量与模拟排放总量的平均绝对相对偏差发现，在该条件下，模型反演背景浓度与模拟的实际背景浓度一致，其偏差极小，小时排放量反演偏差约为5.4%左右，且不同情境下偏差大小基本不变。这表明此时对园区的排放总量反演核算具有较好的效果。

同时，观察到图3中不同时刻的反演偏差有所差异，部分时段的反演偏差明显偏大。从反演机理考虑，该反演过程本质上是利用环境质量监测站点对污染源排放形成的扩散烟羽进行空间采样，再利用采样结果根据污染扩散公式对源排放参数进行约束优化，最终依靠目标函数优化寻找最符合采样结果的源排放参数。因此，采样过程的充分与否将直接影响反演效果。对于固定的污染源和监测点位分布，受气象条件影响的污染扩散烟羽的形态可能对采样造成影响。

为验证该猜想，对不同大气稳定度下的反演差异进行了统计分析(表2) 。结果表明，核算时段内大气稳定度等级主要集中于B、D、E、F这4种情况，总体呈现从A到F (强不稳定到稳定) ，反演偏差逐步增大的规律 (表3) 。参照标准GB/T 3840-91^[15]，反演效果较差的大气稳定度等级E、F主要出现于风速小于3.0 m∙s⁻¹、太阳辐照等级较低的气象条件下。这一条件可能不利于污染物的扩散与传输，污染物空间分布较为集中，不利于监测点位对污染物扩散特征的监测采样，进而导致基于监测数据的反演效果较差。

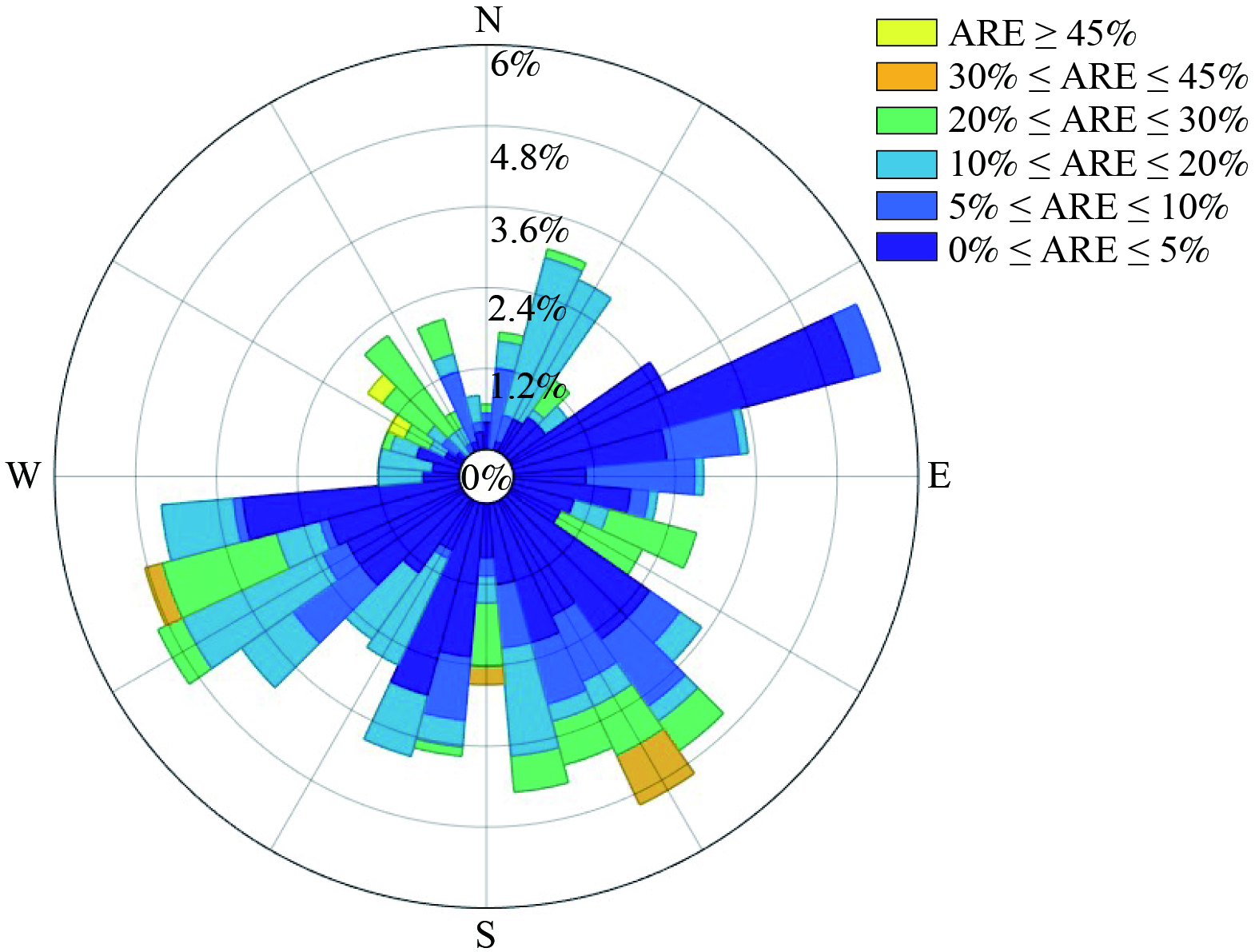
表 2  工业园区大气污染排放总量反演精度模拟评估

Table 2.  Simulation and Evaluation of the Precision of Inversion of Total Air Pollution Emissions in Industrial Parks

情景模式	背景浓度反演偏差 (MARE)	小时排放量反演偏差 (MARE)
低排放情景	(0.00±0.00)%	(5.39±7.43)%
中排放情景	(0.00±0.00)%	(5.33±7.34)%
高排放情景	(0.00±0.00)%	(5.54±7.50)%
周期排放情景	(0.00±0.00)%	(5.33±7.34)%

 | Show Table

DownLoad: CSV

表 3  排放总量反演精度与工业园区大气稳定度的关系

Table 3.  Relationship between the accuracy of total emission inversion and the atmospheric stability of industrial parks

大气稳定度	小时数	平均绝对相对偏差 (MARE)
A	16	(0.00±0.01)%
B	156	(0.62±2.16)%
C	3	(3.40±5.88)%
D	140	(1.03±3.22)%
E	151	(6.07±6.67)%
F	278	(10.08±8.12)%

 | Show Table

DownLoad: CSV

利用风玫瑰图分析反演效果与风向的关系，分析发现反演绝对相对误差 (ARE) 较高的时刻，风向主要分布在西北-东南方向 (图4) 。这一风向与园区主导风向正交。该方向上的反演效果较差可能与该方向监测站点布点相对稀疏有关。

图 4  排放总量反演绝对相对误差 (ARE) 与风向关系

Figure 4.  Relationship between absolute relative error (ARE) of total emission inversion and wind direction

下载: 全尺寸图片 幻灯片

2.2   监测站点布设对反演效果的影响

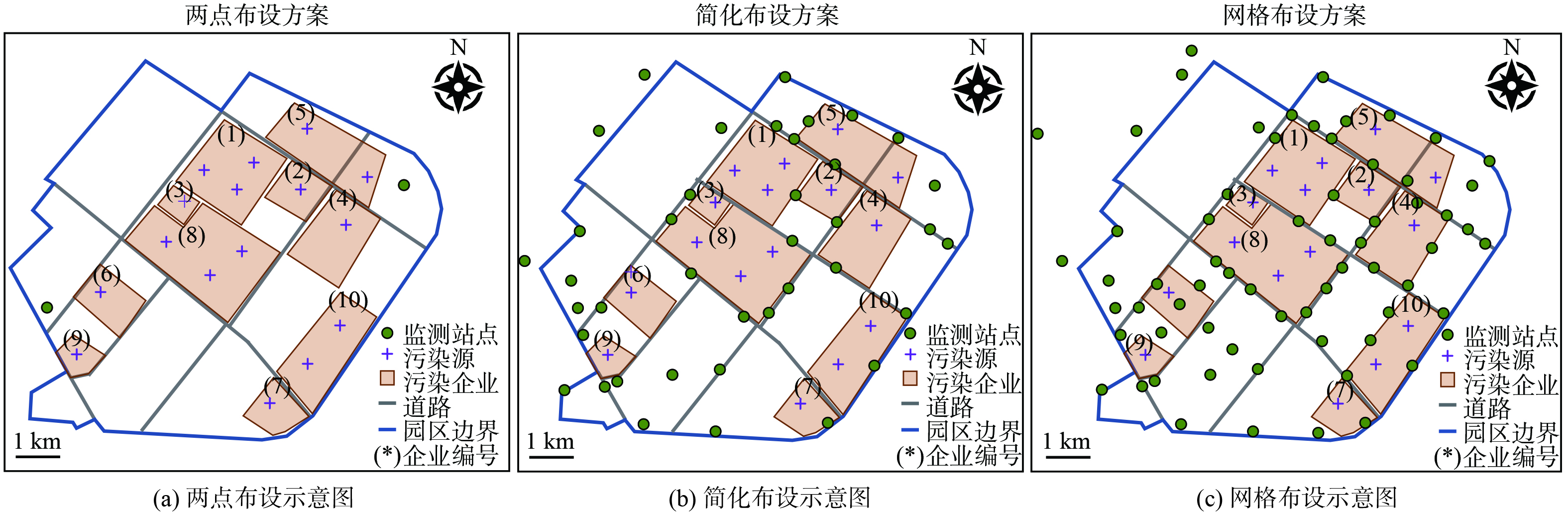
为进一步研究监测点位对反演效果的影响，对比了3种布点方案下的反演精度。两点布设指在园区主导风向的上下风向各布设一个监测点位；网格布设指在园区内及园区边界，依照1~2 km的距离网格式布设监测点位；简化布设则指介于两点布设与网格布设之间的一种情形，对应部分网格布设监测点位失效情形下的反演效果。前文的数据模拟实验是在简化布设条件下进行的。各布点方案的站点位置分布示意见图5。

图 5  3种布点方案示意图

Figure 5.  Schematic diagram of three layout schemes

下载: 全尺寸图片 幻灯片

不同布点方案对反演精度有显著影响（表4）。其中，两点布设方案在4种排放情境下偏差最大，基本无法对园区实际排放量进行有效评估。简化布设方案和网格化布设方案偏差均在可接受范围内。网格化布设方案偏差相比简化布设降低90%以上。因此，网格化布设方案能显著提高园区排放总量核算的精准度。这一结论进一步验证了前述采样充分程度显著影响反演精度的假设。从两点布设、简化布设到网格布设，监测站点的数量增多，对扩散烟羽的采样更加充分，对源排放参数的反演提供了更精确的约束，进而提升了反演的准确度。

表 4  不同布点方案下模型逐小时反演精度评估

Table 4.  Hourly Inversion accuracy evaluation of models under different layout schemes

布点方案	监测站点数	平均绝对相对偏差
		高排放情景	中排放情景	低排放情景	周期排放情景
两点布设	2	(75.55±34.42)%	(75.68±34.20)%	(76.06±33.83)%	(75.56±34.39)%
简化布设*	40	(5.39±7.43)%	(5.33±7.34)%	(5.54±7.50)%	(5.33±7.34)%
网格化布设	76	(0.36±1.55)%	(0.39±1.69)%	(0.48±2.28)%	(0.40±1.83)%
*注：本文2.1节采用简化布设条件，故本行结果采用表2中的数据。

 | Show Table

DownLoad: CSV

2.3   监测站点数据质量对反演效果的影响

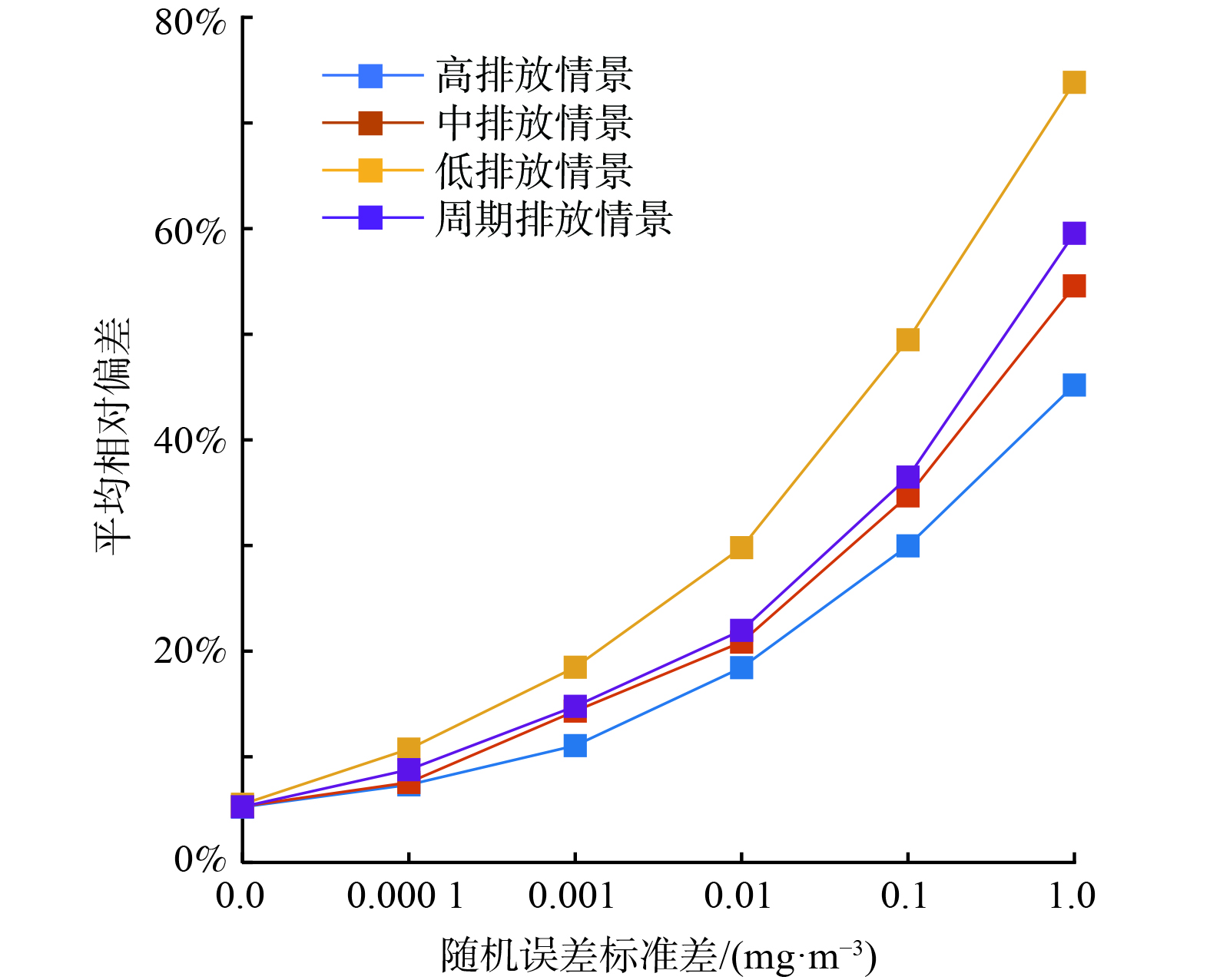
在实际应用中，由于系统误差、随机误差的存在，导致监测站点对污染扩散烟羽的采样可能存在不确定性。对于经过定期校验及规范运维的监测站点，可考虑随机误差为采样误差的主要来源，故本文讨论随机误差对反演精度的影响。依照公式 (5) 模拟不同排放情境下反演精度与随机误差强度的关系。结果表明，公式 (7) 中的正则项显著提高了反演模型在监测数据存在误差时的精度。当不考虑监测误差时，公式 (7) 中的正则项可设置为0 (即不考虑正则化损失函数) ，但当监测数据叠加随机误差时，不考虑正则项将导致反演结果显著偏离模拟实际排放量。以下分析的反演精确度均为通过贝叶斯优化迭代50次后取最佳一阶和二阶正则化系数获得的反演精度。对于本研究的示例园区，正则化因子取值为10⁻⁴到10⁻²⁰之间。

实验表明，在考虑随机误差的情况下，4种排放情景的反演精度存在一定的差异 (这与不考虑随机误差的情况不同) 。反演精度随排放量的增加而提高，低排放情景下反演偏差最大。周期排放情境下的反演偏差则与中排放情景接近。对于低排放情景，随机误差的标准差达到0.01 mg∙m⁻³时，小时反演偏差达到了30%；对于中、高排放情景及周期排放情景，随机误差标准差达到0.1 mg∙m⁻³时，小时反演偏差约为30% (图6) 。即在简化布点方案下，可接受反演误差范围内可忍受的随机误差强度约为0.01~0.1 mg∙m⁻³。以该园区的主要VOCs污染物丙烷为例，在25 ℃常温下，该误差强度相当于5.6~55.6 ppb。该数值大于《环境空气挥发性有机物气象色谱连续监测系统技术要求及检测方法》 (HJ1010-2018) ^[20]规定的监测误差，但小于或相当于《挥发性有机化合物光离子化检测仪校准规范》 (JJF 1172-2007) ^[21]规定的空气微站测量TVOC的误差。这表明采用空气微站监测数据可能会增大对工业园区的VOCs排放总量反演核算偏差。

图 6  不同排放情境下反演精度与随机误差强度的关系

Figure 6.  Relationship between inversion accuracy and random error intensity under different emission scenarios

下载: 全尺寸图片 幻灯片

3.   结论

1) 以东南沿海某石化园区为例，讨论了基于环境监测数据开展工业园区大气污染物实际排放量实时反演核算的技术可行性。该技术可实时动态测算工业园区低矮有组织排放及无组织排放总量的能力，可作为在线监测法、产排污系数法等传统排放总量核算方法的有效补充，提升工业园区基于环境质量开展污染排放动态管控的能力。

2) 基于高斯大气扩散模型及Nelder-Mead优化反演算法，测试并讨论了反演核算方法的准确度及其影响因素。监测站点布设方案显著影响反演核算精度，网格化布点方案有效提高了反演核算精度。监测数据的随机误差显著影响反演核算精度，在简化布点方案下，园区监测站点对VOCs的浓度监测误差应控制在0.1 mg∙m⁻³以下。园区总排放强度对反演核算精度存在一定影响，总排放量大的园区反演核算精度较高。反演核算精度与实时气象条件有关，当气象条件不适宜模型模拟污染物扩散或不适宜监测站点对污染物分布进行有效采样时，可能造成反演精度的下降。

3) 在工业园区开展基于环境监测数据的大气污染物排放总量核算研究具有可行性。同时，监测站点对污染源排放扩散烟羽的采样充分程度是影响反演精度的重要因素。因此，需要在监测站点布设方案比选、监测站点数据质量控制等方面进行精细化管理，以达到最优反演核算效果。