-
随着铁路的高速建设及铁路沿线环保要求的日益严格,隧道废水处理问题日益凸显。目前隧道废水主流处理工艺是采用沉砂、混凝沉淀、水旋澄清、过滤等工艺进行处理,这类工艺对于目标污染物悬浮物 (suspended substance, SS) 的去除率一般可达到60%~85%[1-4]。能够满足现行《污水综合排放标准》 (GB 8978-1996) [5]一级标准中SS为70 mg·L−1的排放要求。但是,一些新建环境敏感区域的铁路已开始执行《地表水环境质量标准》 (GB 3838-2002)[6],部分地区要求SS出水小于10 mg·L−1。同时,由于现场作业面积受限,现场缺乏专业技术人员,对废水除浊设备提出了处理效率高、占地面积小、简单可靠、易于运维的要求。因此,研究隧道施工废水除浊先进技术、开发相应设备、以提高隧道废水除浊处理的效率与效果具有重要的工程应用价值。
当前隧道废水除浊工艺中,水力旋流澄清池因将混凝与澄清工艺集合为一体,简化了工艺流程,使得运行维护较为简便而得到广泛应用。其利用水泵作为唯一动力设备为澄清池提供混凝和接触絮凝驱动力,依靠反应室自下而上的大尺度涡旋的离心作用改善水中胶体颗粒的碰撞效率从而提升絮凝效果,为后续的澄清环节提供接触絮凝悬浮泥渣,从而达到高效化处理的目的[7]。但是,由于该类设备反应室内涡旋尺度较大,导致其处理效率仍旧很低,旋流反应室停留时间达到20~30 min[8]。而近年来以Kolmogrov理论为基础的微涡旋混凝工艺逐步得到应用,该技术主要依靠不同形式的涡旋发生器在混凝流场中形成小尺度涡旋,利用微涡旋增加微粒的碰撞次数,从而提升混凝效率[9-12]。在微涡强化混凝技术研究上,童祯恭等[13]和王艺等[14]在对多孔空心球形涡流反应器进行研究时提出,设置合理的涡流反应器投配组合可以提高絮凝效果;何亚其等[15]提到微涡流混凝器内流体呈现类似于圆管射流的流动特性,法兰构造显著增加了流体的湍流扰动,可有效促进凝聚效率的提升;祝威等[16]提出,气携式涡旋絮凝反应器中可以依靠微气泡在旋流絮凝区中形成微尺度的涡旋,使水流从旋流向涡流转化,从而实现微涡絮凝的目的。
由于隧道现场施工环境较差,若在旋流澄清反应器中直接采用网格或多孔空心球等造涡设备很容易在实际运行过程中发生堵塞,降低设备的可靠性。本研究从水力旋流澄清池的旋流混凝反应区入手,利用自主研发的栅条式微涡发生器作为造涡设备,采用计算机数值模拟手段,探究反应区加入栅条后反应区与絮凝主要相关的流场关键水力学参数变化;并采用模拟废水进行微涡混凝实验验证,拟为隧道废水高效处理工程应用提供参考。
-
1) 物理模型。反应器计算模型如图1所示。反应器为内径110 mm的圆柱体,设置2根内径为6 mm的切向进水管向反应器注水,进水管中心线距离反应器底部为150 mm。为使旋转水流能产生更多数量的微涡旋,本实验在进水管中心线上方50 mm处设置栅条式微涡发生器,以保证旋转水流能不断穿越栅条产生涡旋,同时避免栅条处产生积泥或藻类繁殖。栅条式微涡发生器由10 mm的方形栅条构成,栅条呈十字布置,每侧布置3根栅条,高度分别为200、400、600 mm,栅条两两之间的间距为11 mm。
2) 网格划分。实验过程中采用SolidWorks建立计算模型,采用ICEM软件进行网格划分。为了进一步提高数值模拟精度,对反应器壁面处以及栅条表面的网格进行加密处理,经过多次网格独立性检验,最终计算网格数量为6 754 079。
-
1) 控制方程。根据Fluent计算原理,需对流体问题建立质量、动量、能量守恒方程[17-19]。其中质量守恒方程如式(1)所示。动量守恒方程如式(2)所示。能量守恒方程如式(3)所示。
式中:u、v、w为速度矢量,x、y、z为不同方向上的分量。
式中:ρ为液体密度,
kg⋅m−3 ;t为时间,s ;F为微元体所受力,N 。式中:k为流体传热系数,
W⋅(m2⋅K)−1 ;cp 为比热容,J⋅(kg⋅℃)−1 ;ST 为流体的粘性耗散项,;u为速度矢量,m⋅s−1 。2) 边界层条件及计算模型选择。计算中入口处选择速度入口 (velocity-inlet) ,计算过程中按照表1输入相应湍流强度和水力直径。出口选择压力出口 (pressure-outlet) ,默认出口处为标准大气压。选择Z轴方向为重力方向,设置重力加速度−9.8 m·s−2。
目前,文献中关于絮凝数值计算模拟文献主要以stand k-
ε 以及RNG k-ε 模型对水处理絮凝设备进行模拟计算。结果表明,RNG k-ε 模型中加入旋流修正项,能够更好的模拟旋流场中的涡运动情况[19-23]。因此,本研究亦采用RNG k-ε 模型进行计算。3) 评价指标选取。根据Kolmogolov微涡旋絮凝理论可知,湍流絮凝中应尽可能改变水力条件生成小尺度涡旋,利用涡旋的惯性作用使反应阶段的微小粒子发生自旋,增加颗粒的碰撞几率,在絮粒成长过程中利用相近尺度涡旋的离心及剪切作用使得不同涡旋中的絮粒发生径向碰撞,从而生成致密絮体。在实际的涡旋絮凝过程中,大尺度的涡旋会在水流的粘性作用下逐步分裂为小尺度的涡旋,涡旋中所携带的能量也会发生逐级传递。当涡旋尺度与絮体尺度相近时会最大程度的启发微涡旋絮凝,使得水中微小絮粒发生碰撞。但在雷诺数较高的湍流条件下,水流的粘性作用较小,无法形成,水流中大尺度涡旋的占比较高,水流的掺混分散能力强,但絮凝能力差。因此,在高效水力絮凝过程中通常需要增设折板板、网格等扰流物,使大尺度涡旋尽可能的通过耗散形成小尺度涡旋,从而增强絮凝反应。
而涡旋在流场中的表现形式主要以能量的形成出现,因此选择湍动动能 (以下简称湍动动能k) 及湍动能耗散率 (
ε ) 来表达涡旋絮凝过程中流场的紊动变化。流体区域内的湍动动能k值越大,表明单位质量流体的紊动程度越剧烈,涡旋数量及其剪切力越强,有利于形成较为致密的絮体[21]。湍动能耗散率ε 是指在分子粘性力作用下由湍流动能转化为分子热运动动能的速率。而絮凝效率取决于颗粒与药剂的微观混合程度,而微观混合程度又取决于湍流动能耗散率的大小[23-27]。ε 值越大,湍动动能转化为分子热运动动能的速度越快,颗粒的碰撞几率越高,絮凝过程中的有效能耗也越高。此外,根据絮凝理论可知,絮凝流场内的速度梯度 (velocity gradient,简称G值) 是评价絮凝效果好坏的关键指标之一[9,28]。其中G值越大,表明流场紊动越强较为适合初期混凝,G值较低则适合絮体的絮凝过程。本研究中也采用G值作为混凝流场的评价指标,计算公式见式4。
式中:ρ为水密度,kg·m−3;μ为水动力黏度,N·s·m−2;ɛ为湍动能耗散率,m2·s−3。
同时,根据Kolmogolov的微涡旋理论提示,当流场中的最小涡旋尺度 (见式5) 与絮粒尺度相比拟时,微小絮粒的絮凝效果最好[29-30]。实际絮凝过程中,该数值越小,表明流场中的涡旋尺度越小,流体的耗散越大,能够絮凝的小颗粒数量越多。
式中:
ϵ 为湍动能耗散率,m2·s−3;ν 为水的运动粘度,m2·s−1。综上,数值模拟实验中主要选取特征断面的湍动动能k、湍动能耗散率
ε 、速度梯度G、最小涡旋尺度λ0 进行计算,特征断面依照栅条高度进行选取。 -
1) 絮凝实验方法。实验过程中采用高岭土作为致浊物质,配置浊度为1 000 NTU的原水进行实验,实验过程中采用PAC作为混凝剂,混凝剂投加量为65 mg·L−1。反应柱进口流速为1.5 m·s−1,反应柱停留时间为2.05 min。反应器运行稳定后,在Z=800 mm断面处对絮体样本进行采集。采用图像法[31-33]对絮体样本进行分析。
2) 絮体测试方法。实验实验过程中对絮体取样后采用显微镜对絮体样本进行拍照,利用巴拓图像分析软件识别絮体样本的长轴长L和絮体投影面积A。按照公式 (6) 计算絮体分形维数D2。为防止絮体采样过程中的随机性,絮体样本采集样本不少于50个。
式中:A表示絮体的投影面积,
μm2 ;L表示絮体投影周长,μm 。D2表示絮体分形维数。3) 絮凝实验评价指标。目前对于隧道废水的研究中,由于采用重量法测试SS较为繁琐耗时,普遍采用剩余浊度作为废水处理评价指标[34]。同时废水中的SS浓度与浊度本身存在线性关系,一般SS浓度是浊度的1.62~1.72倍[34,35]。因此本实验实验也采用上清液剩余浊度作为处理评价指标。实验实验中在反应器上方出水口处取上清液,上清液沉淀30 min后测试水样剩余浊度,浊度样品取3组平行样进行测试,取平均浊度作为最终的浊度处理数据结果。
-
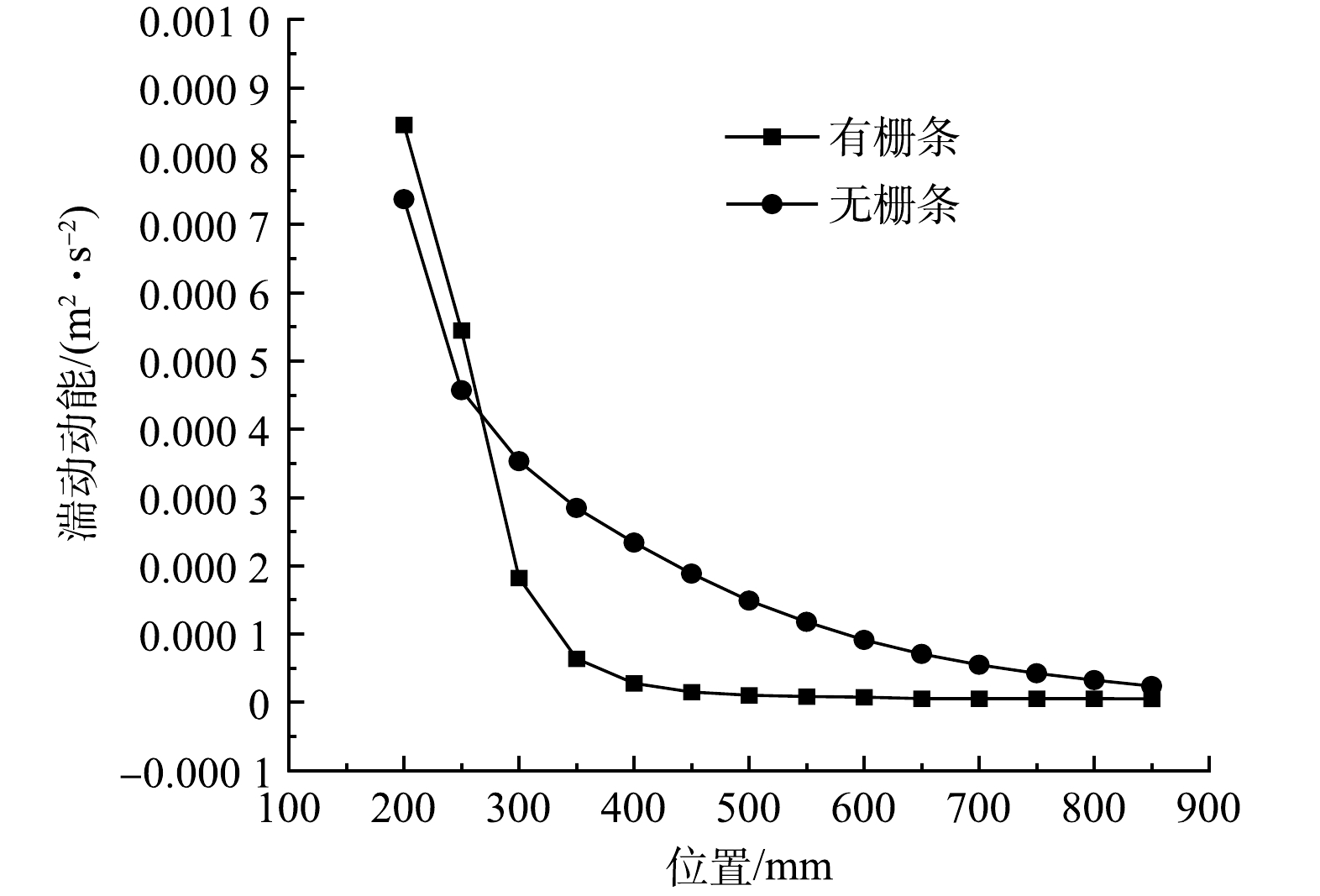
1) 湍动动能分布情况分析。图2为反应器内加入栅条前后湍动动能变化情况云图。由图2可知,旋流场内不加栅条时,沿反应器高度方向呈现均匀递减。湍动动能波动呈现同心圆分布,除反应器边界层以外,在反应器断面半径为200~300 mm的圆环区域内波动最为强烈,整体的流场内波动主要依赖于水流沿径向出流的动力与自身所受重力2种,流场内分层较为明显,呈现“类层流”的分布方式。这种类层流的旋流方式利于微小絮粒发生同向絮凝作用,但由于流场内的紊动较为稳定,因此旋流场内的涡旋尺度式中较大,其剪切作用很弱,无法将絮体增密。
流场中加入栅条后,水流在进入反应器后与栅条发生碰撞产生剧烈的速度激变,在栅条迎流面处产生最大湍动动能,Z=200 mm和Z=300 mm处平均湍动动能分别达到8.46×10−4、5.45×10−4 m2·s−2,较之无栅条情况分别增加14.76%、19.24%。而在每组栅条背部由于流体整流及边界层剥离作用会形成一个类三角的低湍动动能区域,流体在激变过程中产生较大的速度梯度变化,利于在短时间内让颗粒发生碰撞形成絮粒,利用涡旋的离心惯性絮凝作用和剪切絮凝作用,致使松散絮粒进一步破碎再絮凝从而形成致密絮粒[29,36]。
图3为反应器加入栅条前后反应器各特征断面平均湍动动能变化图。由图3可知,流场内加入栅条后,湍动动能沿反应器高程会迅速衰减,根据Kolmogrov涡旋理论可知,湍动动能主要包含在大涡中,而小尺度的涡旋含能较少[26]。由此可知,栅条的引入会使旋流场中原本存在的大涡漩迅速分割为小尺度涡旋,小尺度涡旋在进一步的粘性耗散下形成Kolmogolov级别的涡旋,从而加速微小絮粒的涡旋絮凝过程。同时,涡旋在进行能量传递的过程中,不同尺度的涡旋在能量转换过程中不断由大涡演变为小涡,而流场内大涡的外缘线速度大于小涡的外缘线速度,进而在涡旋演变区间内形成大量的局部速度梯度变化区,利于颗粒在涡旋区迁移时发生碰撞。
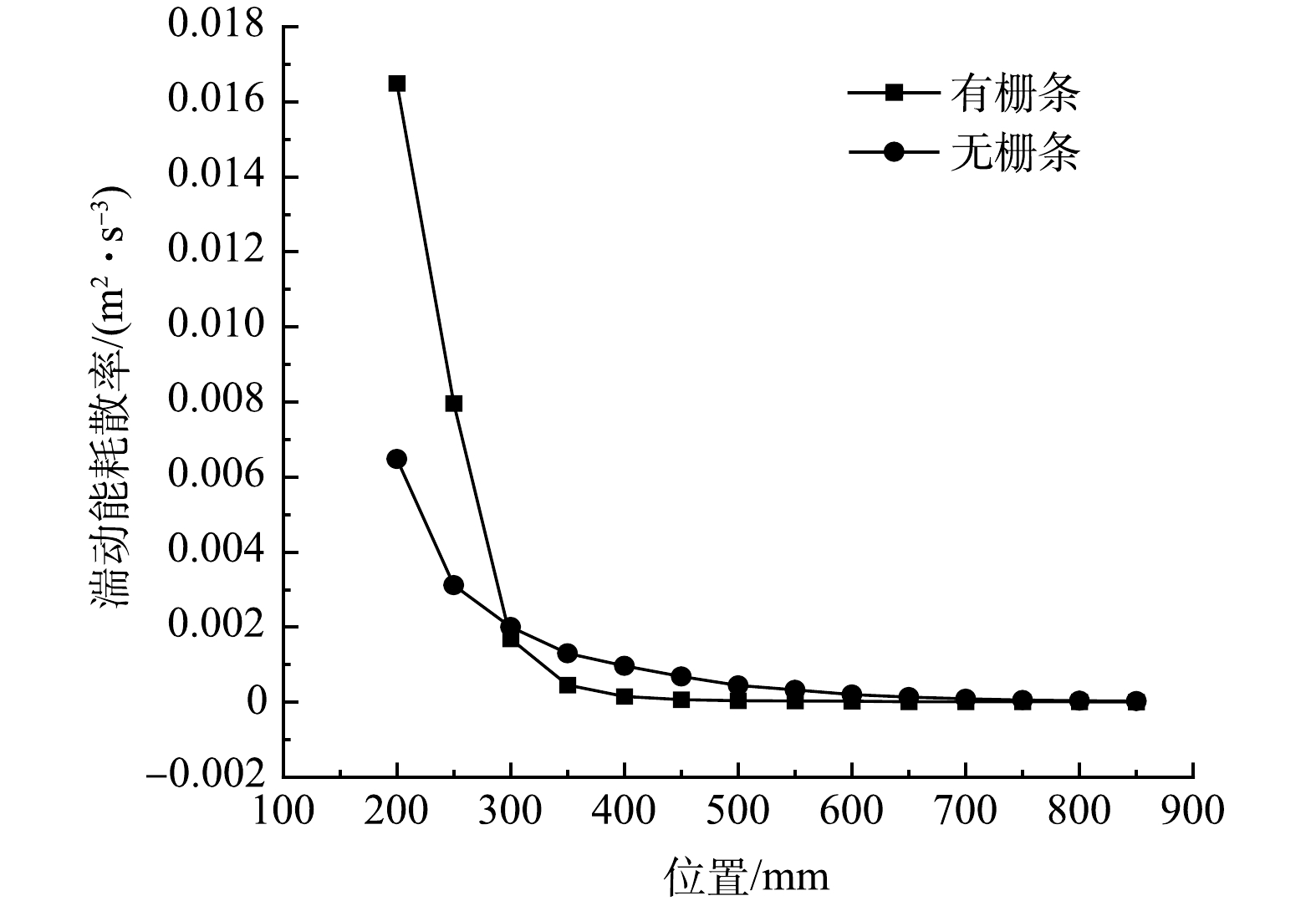
2) 湍动能耗散率分布情况分析。图4为反应器内加入栅条前后湍动能耗散率变化情况云图。由图4可看出,在无栅条情况下,流场内的湍动能耗散率主要分布在反应器边壁处。其原因在于,旋流场条件下边壁处存在过渡区和紊流区,过渡区流层极薄,但易产生较为强烈的边界层剥离现象,进而增加流层的湍动能耗散率。由于流场内无其它扰流物,因此反应器内半径52 mm的区域内并无强烈湍动动能耗散变化情况。由于湍动能耗散率是依照单位质量的流体在单位时间内损耗的湍动动能来衡量的。因此,沿高程方向
ϵ 变化规律与k相同[37]。当流场内加入栅条后,湍动能耗散率的最大值由反应器边壁处转移至栅条表面,其中栅条的迎流面尖角处
ε 值最大。在反应器Z=200~300 mm区间内,ε 值分别达到1.65×10−2、7.9×10−3 m2·s−3。较之无栅条情况下急剧增加;z=200 mm和z=250 mm断面的ε 值增加154.48%、155.59%。这将有利于更小尺度的微涡旋产生,促进初始颗粒的碰撞聚集。而在z=300 mm后,水流的旋流作用减弱,湍动动能值降低,栅条流场内的耗散进一步减弱,到z=700 mm后,2种流场内的ε 值逐步趋同。图5为反应器加入栅条前后反应器各特征断面平均湍动能耗散率变化图。由图5可看出,反应器内有栅条时,絮凝反应初期团
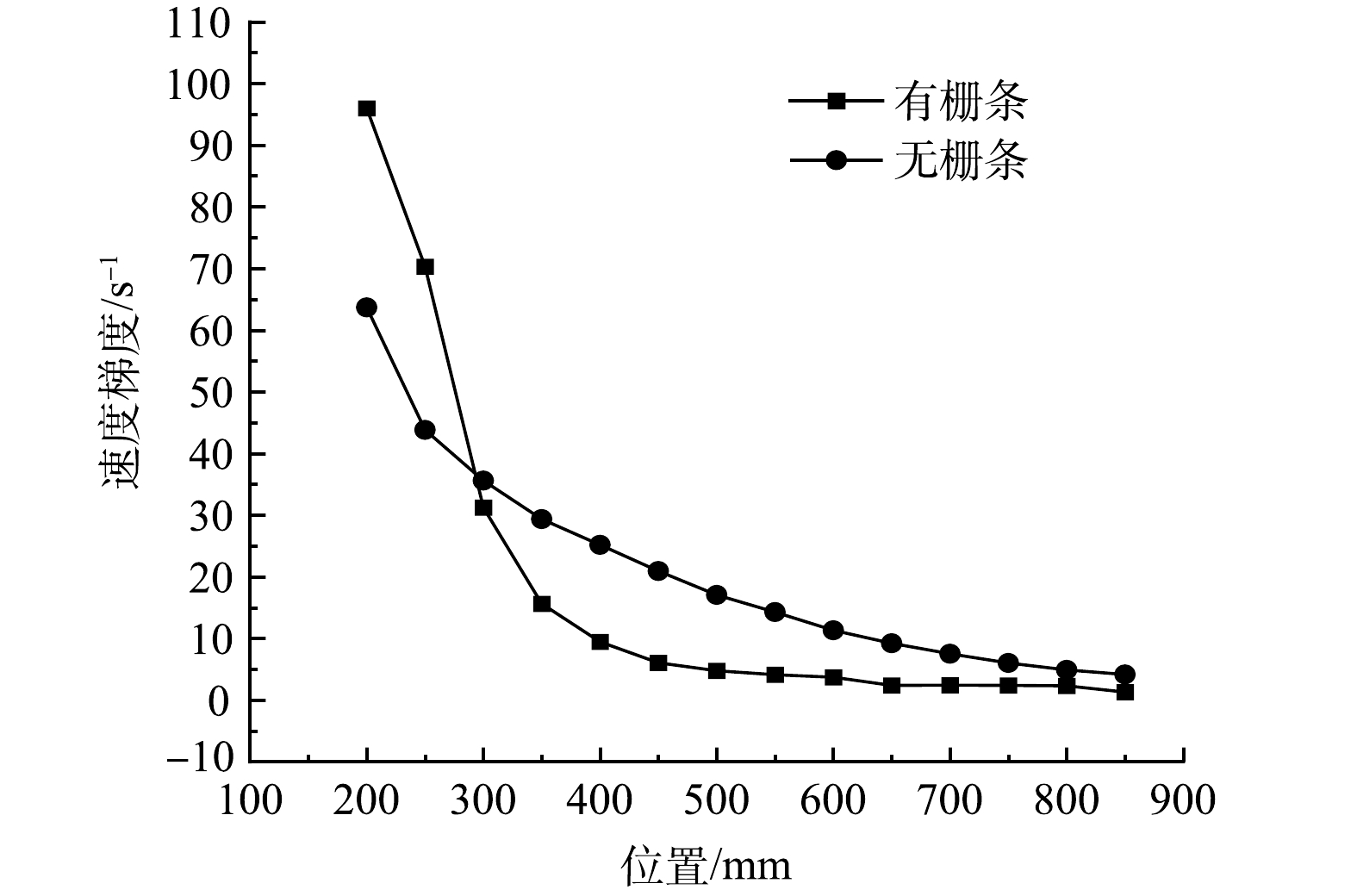
ε 值较大,利于微小颗粒与药剂在微观程度上进行充分、有效的混合;随着反应进行,水流自下而上运动,除克服重力外还需抵抗栅条的阻流作用,ε 值也随之缩减。这种ε 值的减小利于在絮凝反应的中期后期产生与成熟絮粒尺度相宜的涡旋,使得微小絮粒可在相宜尺度涡旋下发生剪切、碰撞、增密等作用;同时,已形成的成熟絮体将不再受高速水流的冲击。3) 速度梯度G值分布情况分析。图6为反应器内加入栅条前后速度梯度G值变化情况云图。图7为反应器加入栅条前后反应器各特征断面平均G值变化图。由图6、图7可看出,当流场内无栅条时,速度梯度G表现方式与湍动能耗散率
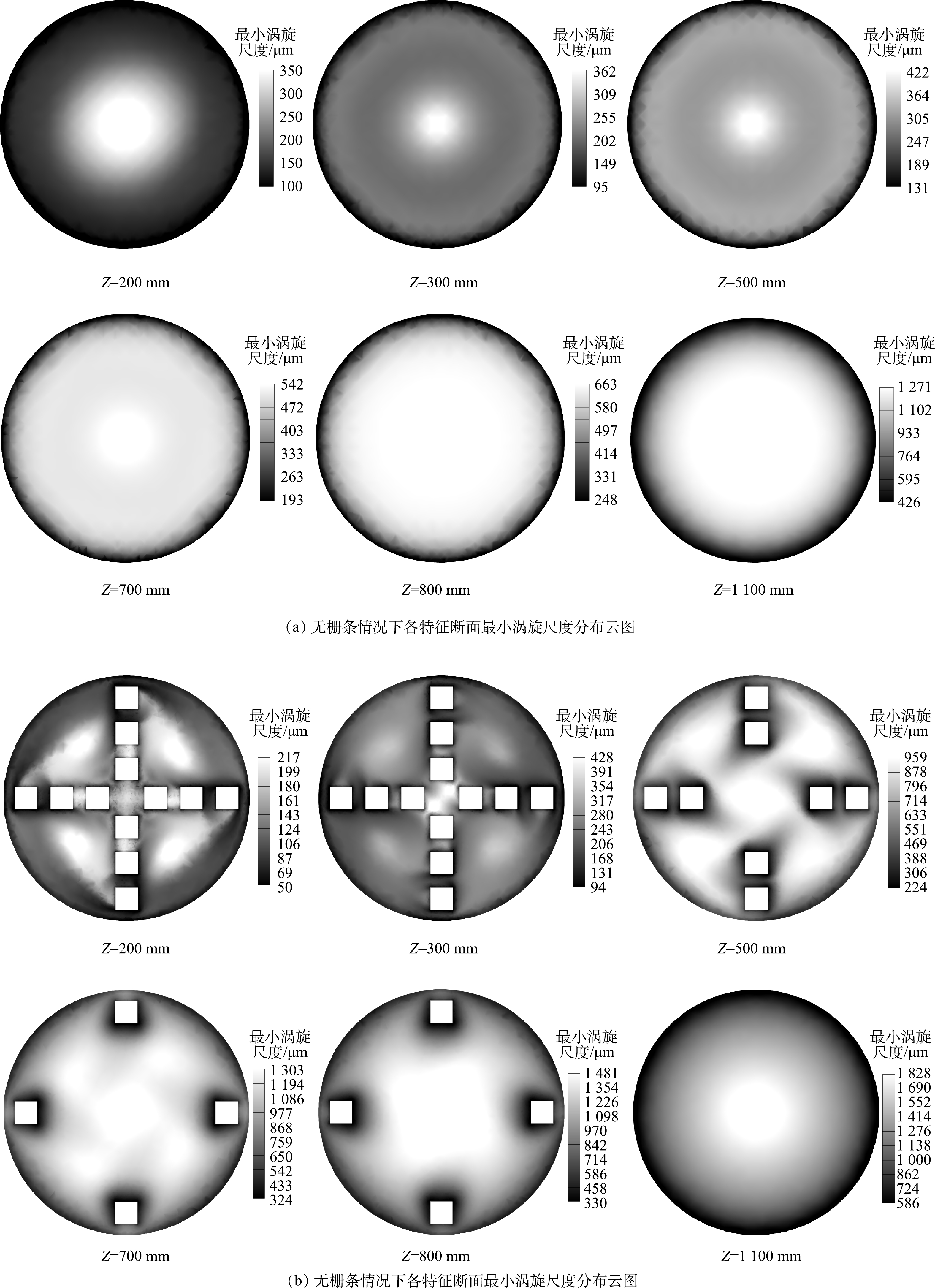
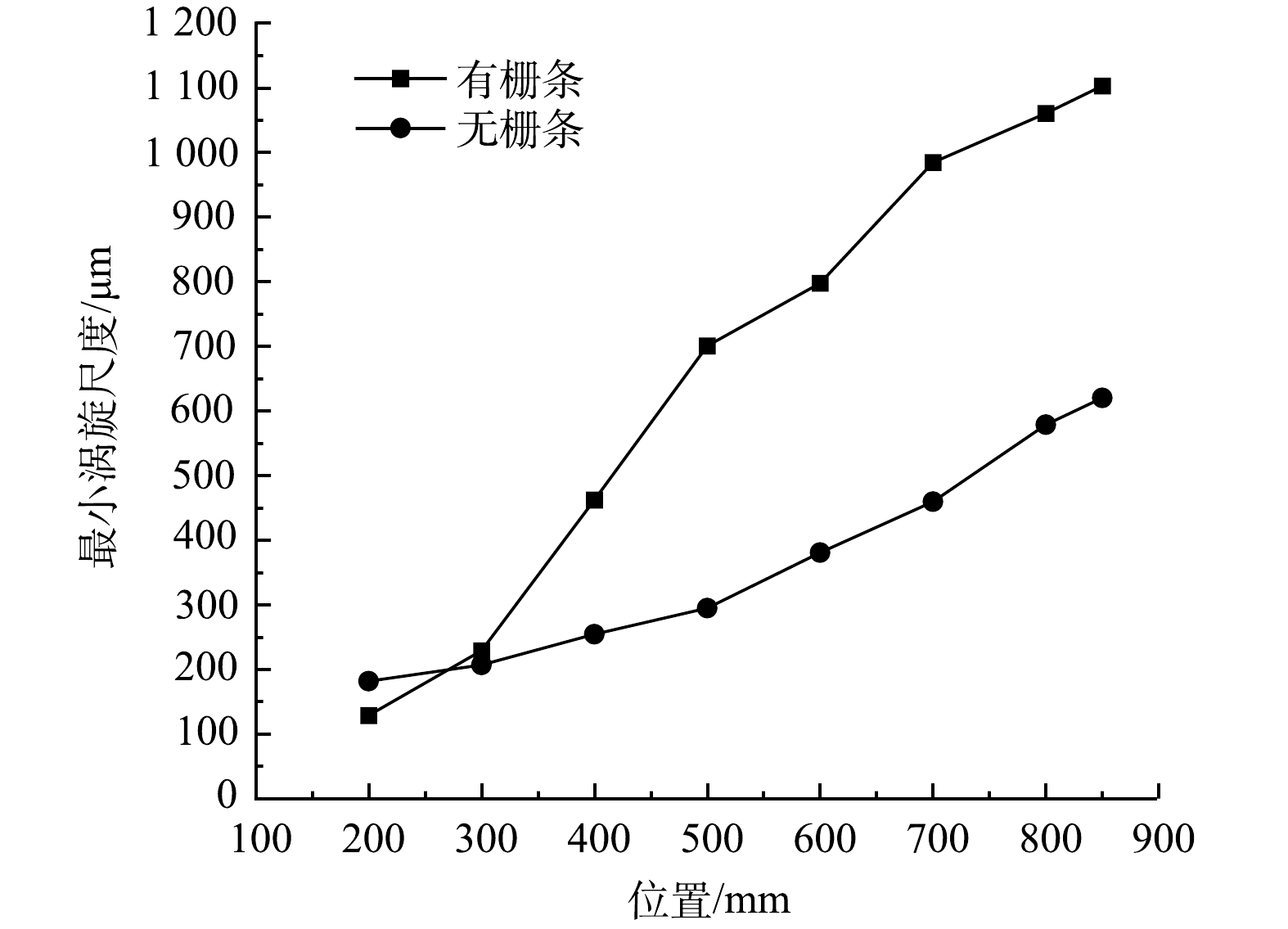
ε 近似,均为边壁沿径向向中心递减,在Z=200~500 mm的区域内,G值云图呈现同心圆结构。而在流场内加入栅条后,G值在絮凝反应的初始区域 (Z=200~250 mm) 内急剧增高,相比无栅条情况下G值增加近55%,在絮凝反应中段 (Z=300~450 mm) 的区域内,有栅条流场G值逐步降低,其均值分布均低于无栅条流场。这种大梯度的坡降将利于絮体的完整成长。而在絮凝反应中后段 (Z=500~800 mm) 的区域内,G值逐步趋于稳定,不会对已形成絮体造成剪切破坏。4) 最小涡旋尺度分析。图8为反应器内加入栅条前后最小涡旋尺度分布云图。由图8可知,当流场内不加栅条时,微涡旋主要分布在流场中心区域,与湍耗散分布情况相反,最小涡旋的尺度由反应器外侧向圆心处逐步增大,在z=200 mm断面处,Kolmogrov涡旋尺度为60~380 μm,且涡旋尺度沿反应器高程逐步增加;当水流进一步运动至z=800 mm处,涡旋尺度最大可达到660~680 μm,这种沿高程的涡尺度增长方式与絮体尺寸由小变大的趋势相同,较为絮体的增长凝聚方式。当流场中加入栅条后,z=200 mm处的涡旋尺度分布变为40~220 μm,到z=800 mm断面处,涡旋尺度增加至300~1 500 μm。由此可得,流场中加入栅条后会明显改变涡旋尺度的分布方式,即初始流场涡旋尺度小,范围窄,末端流场尺度大、范围大。这将有利于初始小颗粒在小尺度涡旋内聚集,当絮体在末端流场增长到一定尺度时,流场涡旋尺度大,利于絮体的进一步聚集。
图9为反应器加入栅条前后反应器各特征断面最小涡旋尺度变化图。由图9可知,流场内加入栅条后会明显增加涡旋尺度的变化速率,提高中等尺度涡旋 (400~800 μm) 的分布密度,为相近尺度的絮体提供更好的聚集条件。同时涡旋平均分布尺度从128~1 100 μm,跨度较大,利于反应器内不同尺度的絮体的强化絮凝。
-
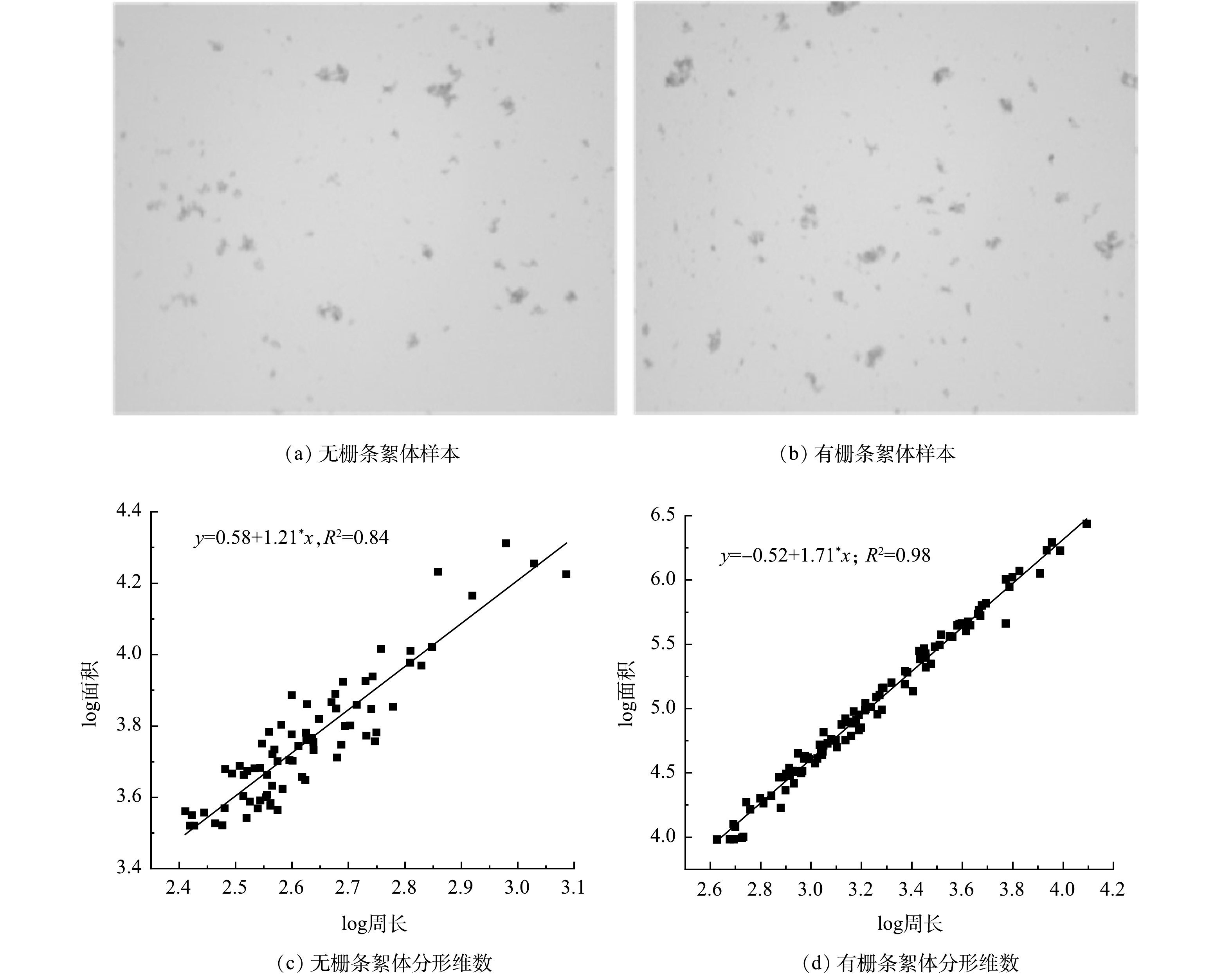
1) 絮凝实验结果分析。图10为两种流场条件下絮体样本照片以及分形维数。在无栅条情况下,絮体尺寸较大且较松散,分形维数仅为1.21。上清液最终剩余浊度为110.3 NTU,去除率可达88.97%;流场中加入扰流栅条后,微粒在微涡旋作用下结团效果明显,絮粒整体尺度较小,但其沉降性能较好,分形维数可达1.71。上清液最终剩余浊度为37.4 NTU,去除率可达96.26%。这表明,在流场中加入栅条形微涡发生器后混凝效果较好,上清液最终浊度较之无栅条时下降66.09%,流场中涡旋的剪切作用及惯性絮凝作用明显,所形成絮体体积小密度大,能有效改善颗粒在涡流场中的混凝环境。
-
1) 流场中加入栅条式微涡发生器后,湍动动能及湍动能耗散率提升明显,有利于混凝反应初期药剂与颗粒的充分混合。同时,流场中引入栅条后,其紊动更加混乱不均,破坏了无栅条时的“类层流”同心圆分布的流场结构。持续的紊动将利于颗粒发生多种形式的絮凝。
2) 流场中引入栅条式微涡发生器后,流场内可产生尺寸范围角广的微涡旋,其中400~800 μm尺度涡旋占比较高,可为相近尺度的絮体能够提供更好的聚集条件。
3) 流场中加入栅条式微涡发生器后,反应器的停留时间仅为2 min较之旋流式水力循环澄清池的旋流反应区20~30 min的停留时间有明显提升。在同等实验条件下,涡旋絮凝反应后的絮体更加密实,其分形维数可达1.71,同时上清液出水浊度可达37.4 NTU去除率可达96.26%,较之无栅条时有明显提升。
栅条式微涡除浊技术流场数值模拟
Numerical simulation of flow field in grid micro-vortex for turbidity removal technology
-
摘要: 针对铁路隧道施工废水的高精度高效率除浊需求,采用在旋流式澄清池的旋流反应区中加入栅条式微涡发生器的方式来提升设备混凝除浊效率。采用数值模拟手段分析了旋流场内加入栅条前后流场内与混凝有关的特征参数变化,并采用水力实验进行效果验证。结果表明,加入栅条后,混凝流场初始段的湍动动能及湍耗散明显提升,较之空池条件下分别提升19.24%、155.59%。这种变化利于混凝反应初期,药剂的充分分散,增加颗粒的初始碰撞概率。同时,栅条引入后,增加了流场内的涡旋尺度分布范围,利于流场内不同尺度颗粒完成涡旋絮凝。在原水浊度1 000 NTU的条件下,带有栅条的反应器最终上清液出水浊度达37.4 NTU,絮体分形维数可达1.71,较之空池情况下有明显提升。本研究结果可为微涡旋絮凝技术用于隧道废水处理提供参考。Abstract: According to requirements of high efficiency turbidity removal in construction wastewater of railway tunnel, spoiler grids were added in the swirling flow field to improve the efficiency of colloidal particle flocculation. Numerical simulations were used to analyze the changes of coagulation-related characteristic parameters in the swirling flow field with grids or not, and hydraulic tests were used to verify the effect. The results showed that the turbulent kinetic energy and turbulent dissipation in the initial section of the swirling flow field were significantly improved by 19.24% and 155.59%, respectively, compared grids with non-grids condition. This change facilitated the full dispersion of the flocculant and increased the initial collision probability of the particles at the early stage of coagulation reaction. Meanwhile, the increase of the vortex average scale range could facilitate the vortex flocculation formation of particles in different scales in the swirling flow field. Under the condition of raw water turbidity of 1000 NTU, the supernatant turbidity of the reactor with grids reached 37.4 NTU and the floc fractal dimension reached 1.71, which was a significant improvement compared with the case without grids. The results of this study can provide references for efficient turbidity removal technology for tunnel wastewater.
-
烟气经湿法脱硫后会产生大量含可溶性物质的白色水雾[1],导致环境污染[2]。除雾方法主要是加装除雾器[3],如折流板除雾器[4]、丝网除雾器[5]、静电除雾器等[6]。为提高除雾器的气液分离作用,NARIMANI 等[7]运用CFD的方法优化了带倒钩的折流板除雾器结构;EL-DESSOUKY 等[8]研究了不同网层厚度下丝网除雾器的最佳过滤风速;袁惠新等[9]研究了旋风除雾器在引入静电场后对细水雾的脱除效果。然而,目前水雾排放浓度依然难以达到相关标准规定的排放限值[10]。因此,白色烟羽排放的有效控制已成为湿烟气深度净化的一个研究热点[11-12]。
烟气“脱白”技术鲜有突破,其原因是除雾工程应用限制了2个高效技术路径:要求成本低、能耗少、占地小,不宜采用湿电;要求压损小、无堵塞,不能采用过滤。因此,近年来利用空气动力分离的技术方法倍受关注[13-15]。然而,采用空气动力分离除雾,需要在细而长的螺旋管中带动整个气流高速旋转,导致能耗过高,而且细水雾易被高速气流带出除雾器。
为实现高湿烟气的高效除雾,笔者提出了自由旋线除雾方法[16-17],并开展了单层自由旋线除雾实验研究[18]。结果表明,自由旋线除雾器的压损小、效率高,并且发现在控制能耗情况下增加旋线根数比增加旋线转速的提效作用更显著。然而,关于自由旋线除雾器的除雾性能还缺乏基础理论研究。本研究将基于经典的单根柱状纤维捕集和旋流离心分离机理,建立自由旋线除雾器的除雾效率理论,并通过实验加以验证,进而揭示旋线根数和转速对自由旋线除雾作用的影响规律,以期为自由旋线除雾技术的发展及应用提供参考。
1. 旋线除雾理论
1.1 旋线除雾器的工作原理
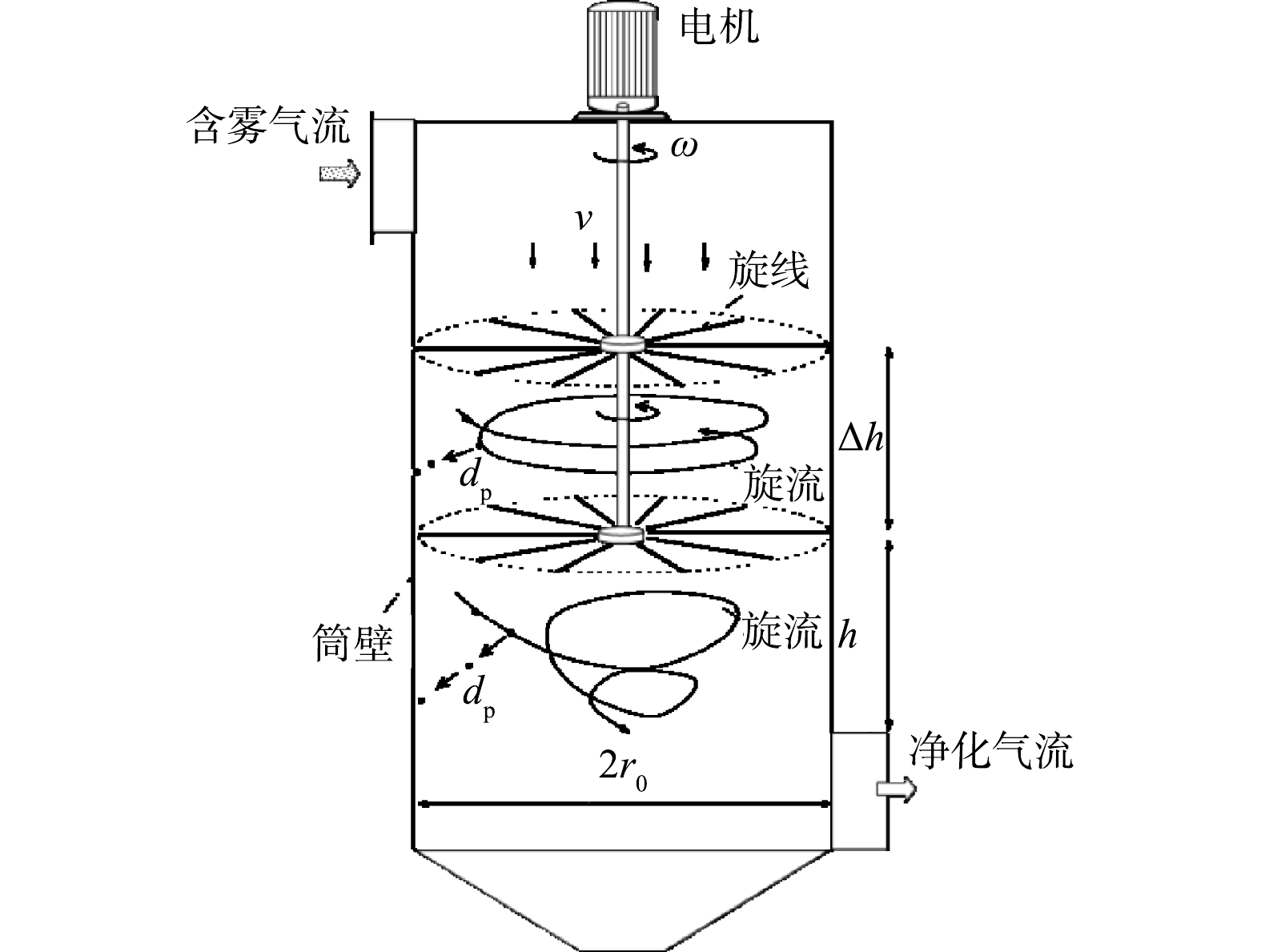
在旋线除雾器中布置有数以百计的纤维线(见图1)。纤维线的一端固定在电机的连接轴上,纤维线的另一端自由。电机启动前,纤维线在自重作用下自然下垂。电机启动后,高速旋转的纤维线(简称旋线)在离心力作用下呈伞形张开,并覆盖整个除雾器筒体过流断面。
当含雾气流进入除雾器,在通过旋线层时,柱状纤维旋线与液滴间产生拦截、惯性碰撞和扩散作用[19]。由于纤维线具有吸湿性,液滴会附着旋线表面或浸入旋线中,然后在离心力作用下甩向筒壁。筒壁上的液体在重力作用下最后流入除雾器底部的液斗中。另外,由于高速旋转的纤维线搅拌作用,使旋线层下方的气体形成旋流,进而对未被捕集的液雾产生离心分离作用,使旋线除雾器的净化效果得到进一步提升。所以,旋线除雾器的工作原理是旋线层过滤和旋流离心分离的协同作用。
1.2 旋线层的除雾效率
当圆柱状纤维与垂直于来流方向颗粒物之间的相对速度相同时,基于孤立圆柱状捕集体对颗粒物的捕集机理来探索纤维层的捕集效率更容易[20]。但由于旋线与雾滴的相对速度是变化的,需先根据不同的捕集机理确定单根旋线的捕集量,然后由效率定义分别建立旋线层的拦截、惯性碰撞和扩散效率理论表达式。
1.2.1 拦截
分析纤维对颗粒物的拦截捕集作用首先要考虑绕捕集体流动的介质的流态。对于绕流问题,分为黏性流和势流。判断流态的依据是雷诺数(Re),具体见式(1)。
Re=ρvdfμ (1) 式中:ρ为空气密度,kg·m−3;v为空气流速,m·s−1;df为旋线直径,m;μ为气体动力黏性系数,常温常压下,μ=1.85×10−5 Pa·s。
当Re≤1时,柱状捕集体周围的流动可视为黏性流;而当Re>1时,可近似为势流[21]。在自由旋线除雾器中,旋线的切向速度可超过10 m·s−1,且旋线较粗(直径通常2~4 mm)。由此得出,气流绕旋线流动的雷诺数Re超过100,属势流。在势流情况下,单位长度孤立圆柱状捕集体对球形雾滴的拦截效率计算公式[22]见式(2)。
ηr=1+G−11+G (2) 式中:ηr为单位长度孤立圆柱状捕集体对球形雾滴的拦截效率;G为拦截参数,计算式为式(3)。
G=dp/df (3) 式中:dp表示雾滴直径,m;df为旋线直径,m。
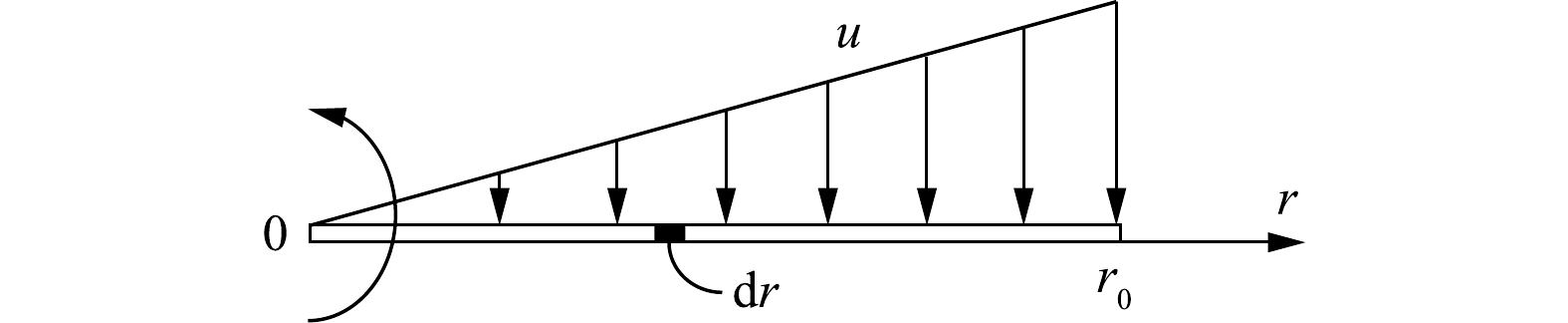
然而,沿旋线上的切向速度u是不均匀的,切向速度分布如图2所示。于是,旋线上任意点r与颗粒的相对运动速度见式(4)。
u=ωr (4) 式中:u为旋线与颗粒的相对速度,m·s−1;ω为旋线旋转角速度,rad·s−1;r为旋线半径,m。
设气体中的颗粒初始浓度为c0,在图2所示的旋线微元长度dr上拦截的雾滴质量计算式见式(5)。
dmR=c0ηrdfudr=c0ηrdfωrdr (5) 式中:dmR为微元dr上拦截的雾滴质量,kg;c0为气体颗粒浓度,kg·m−3。
对式(5)从0到旋线长度r0进行积分(见式(6)),得到单根旋线拦截作用捕集的雾滴质量。
mR=∫r00c0ηrdfωrdr=12c0ηrdfωr02 (6) 因流向孤立旋线的雾滴总质量的计算式见式(7)。于是,单根旋线拦截作用的捕集效率可通过式(8)进行计算。
M=Qc0=πr02vc0 (7) ηR=mRM=ωdf2πvηr (8) 式中:M为来流雾滴总质量,kg;Q为气流流量,m3·s−1;c0为气体颗粒浓度,kg·m−3;v为通过旋线除雾器筒体断面的平均轴向速度,m·s−1;ηR为单根旋线拦截作用的捕集效率;mR为单根旋线捕集雾滴质量,kg。
对于气流中有N个捕集体时(见图3),由计算式(9)[23],得到旋线层的拦截效率。
ηRN=1−(1−ηR)N (9) 1.2.2 惯性碰撞
当颗粒直径dp>1 µm,柱状捕集体的惯性碰撞效应是重要的。惯性碰撞效率是Stokes数St的函数,其表达式见式(10)。
St=ρpdp2u18μdf (10) 式中:ρp为雾滴密度,kg·m−3;dp为雾滴直径,m;u为捕集体与颗粒的相对速度,m·s−1;μ为气体动力黏性系数,取μ=1.85×10−5 Pa·s;df为旋线直径,m。
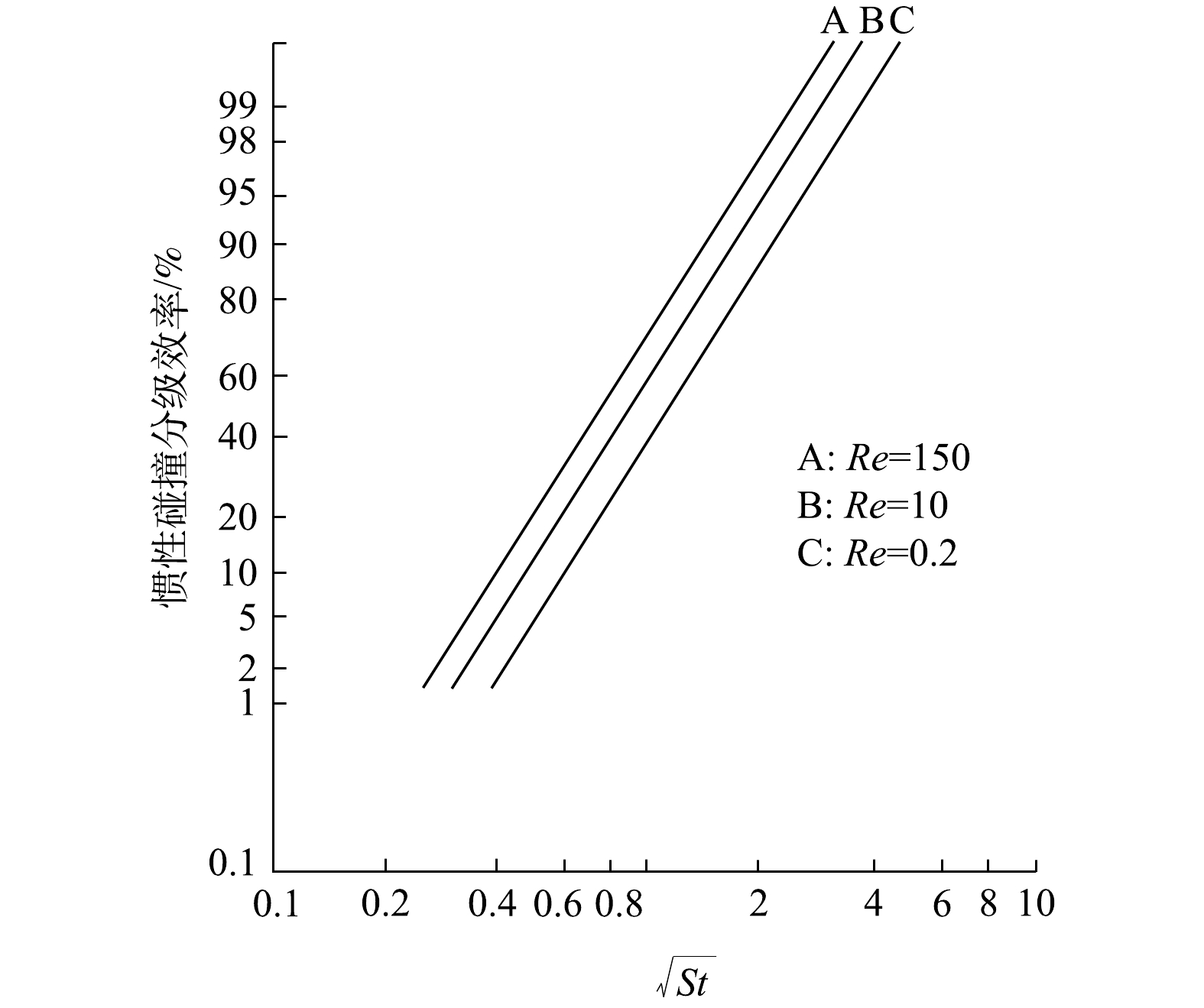
由于绕孤立柱状纤维流动的颗粒运动方程求解非常困难,至今没有分析解。虽然LANDAHL和HERMAN给出了惯性碰撞效率经验式[22],但在高雷诺数的势流情况下缺乏适用性论据。已有研究结果表明,在对数概率坐标纸上,单位长度孤立柱状捕集体的惯性碰撞效率随
√St 而能在对数概率坐标纸上具有直线分布特征的数学模型为对数正态分布。于是,惯性碰撞效率与
√St ηi=1lnσg√2π∫√St0exp[−(ln√St−ln√St50)22(lnσg)2]d(ln√St) (11) 式中:ηi为单位长度孤立圆柱状捕集体的惯性碰撞效率;σg为几何标准偏差;
(√St)50 对于旋线,符合Re≥150,满足曲线A,于是由图4可确定
(√St)50=0.7 σg=√St(ηi=84.1%)(√St)50=1.350.7≈1.9 (12) ηi=1ln1.9√2π∫√St0exp[−(ln√St−ln0.7)22(ln1.9)2]d(ln√St) (13) 来流颗粒与旋线的相对运动速度是变化的,故单根旋线上惯性碰撞捕集的液滴质量可由积分(见式(14))来计算。单根旋线的惯性碰撞捕集效率计算见式(15),而气流中有N根捕集体的惯性碰撞效率计算式见式(16)。
mI=∫r00c0ηidfωrdr (14) ηI=mIM=ωdfπr02v∫r00ηirdr (15) ηIN=1−(1−ηI)N (16) 式中:mI为单根旋线惯性碰撞作用捕集的液滴质量,kg;ηI为单根旋线的惯性碰撞捕集效率;ηIN为旋线层惯性碰撞捕集效率;N为旋线根数。
1.2.3 扩散效应
扩散效应适合于颗粒直径dp<1 µm的情况。但在水雾中,dp<1 µm液滴所占质量百分比极小,对总捕集效率的贡献很小,可忽略。
对于多机理同时存在的复合捕集效率,普遍采用RICHARD和SEINFELD 给出的算式[25] (见式(17))。于是,N根旋线的旋线层的拦截和惯性碰撞复合除雾效率计算式见式(18)。
η=1−(1−η1)(1−η2)⋯(1−ηn) (17) ηN=1−(1−ηRN)(1−ηIN) (18) 上述研究表明,降低气流速度、增加转速,均有助于增强拦截和惯性碰撞的捕集作用,但增加旋线根数的提效作用更突出。
1.3 旋流离心分离
旋线除雾器可采用单层或多层布置。由于每层旋线布置的根数是受限的,当旋线除雾器无法满足水雾排放要求时,可通过增加旋线层数提效。当采用多层布置时,在两旋线层之间形成较规则的旋涡流,对雾滴产生离心分离作用。
图1中,旋线层间的距离Δh应不小于旋线长度
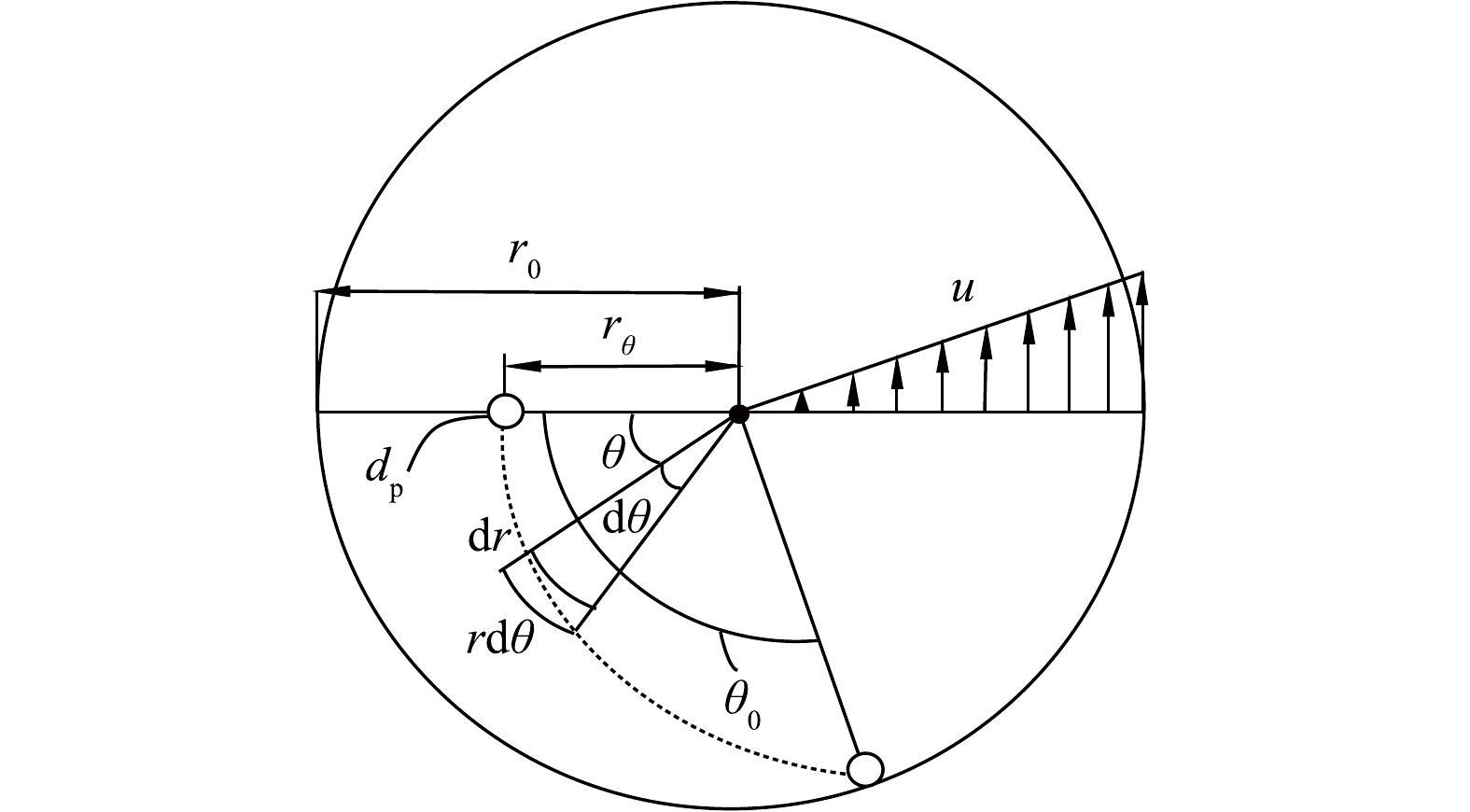
r0 t0=Δh/v (19) θ0=ωt0=ωΔh/v (20) 在图5所示的旋流场中,假定位于半径rθ直径为dp的雾滴随气流旋转θ角度后,沉降到r=r0的边壁上被捕集。
显然,对于位于rθ和r0之间直径为dp的所有雾滴将被捕集。因此,其旋流分离效率计算式见式(21)。
ηω=(r0−rθ)/r0=1−rθr0 (21) 由式(21)可知,下面应确定rθ的计算方法。在图5所示的雾滴轨迹线的任意点(r, θ)上,雾滴在dt时间内径向和切向运动距离计算式见式(22)。
dr=wdt,rdθ=udt (22) 式中:雾滴的离心沉降速度w计算式见式(23)。
w=τu2r (23) 式中:τ为弛豫时间,计算式见式(24)。
τ=ρpdp2Cc18μ (24) 式中:Cc 即Cunningham 滑移修正系数,对于dp>1 µm的粒子,Cc≈1。
由式(22)可换算得到式(25)。将式(23)代入式(25),得到式(26)。将式(4)代入式(26),积分得到式(27)。由式(27)得到式(28)。将式(28)代入式(21)得旋流离心分离效率计算式(29)。将式(20)代入式 (29),旋流离心分离效率还可由式(30)计算得到。
drdθ=rwu (25) dr=τudθ (26) ∫r0rθdrr=∫θ00τωdθ (27) rθ=r0e−ωτθ0 (28) ηω=1−rθr0=1−e−ωτθ0 (29) ηω=1−rθr0=1−exp(−τΔhω2v) (30) 可见旋流离心分离除雾效率服从指数变化规律,且是雾径和转速平方的函数。在图1所示的第二层旋线下面仍有呈锥状收缩的旋流流动,但因接近气流出口,旋流衰减较快,故忽略其离心分离作用。
于是,双层旋线捕集和旋流离心分离协同除雾效率计算式为式(31)。
ηC=1−(1−ηN)2(1−ηω)=1−[(1−ηRN)(1−ηIN)]2(1−ηω) (31) 2. 旋线除雾理论的验证
2.1 实验系统
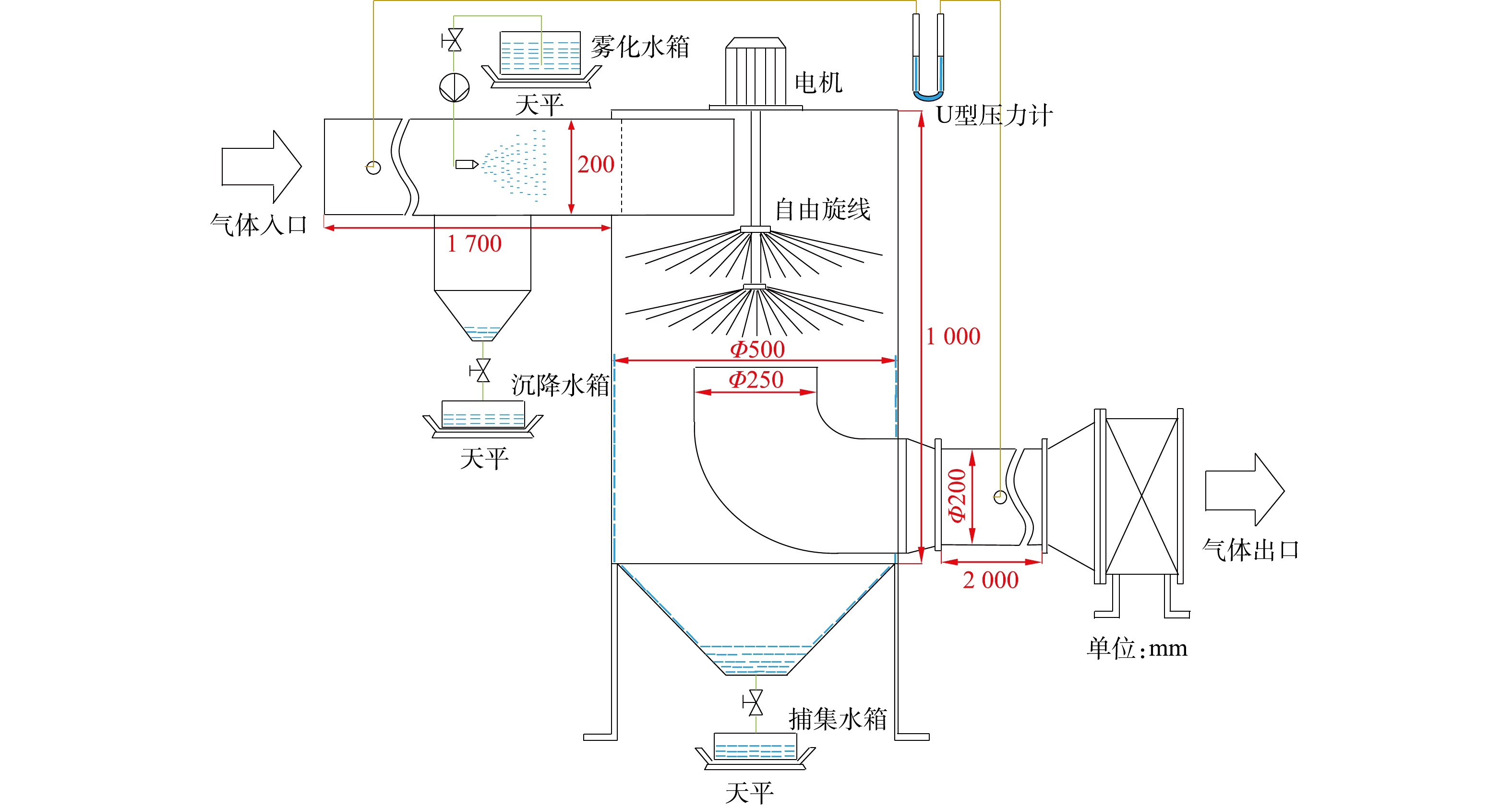
双层旋线除雾实验系统如图6所示。由除雾器本体、水泵、电机、旋线、风机、水箱构成。入口管均布4个雾化喷嘴,壳体采用8 mm厚有机玻璃,旋线长250 mm,材质采用3 mm聚酯纤维线。风机最大风量5 000 m3·h−1,全压300 Pa。
2.2 实验方法
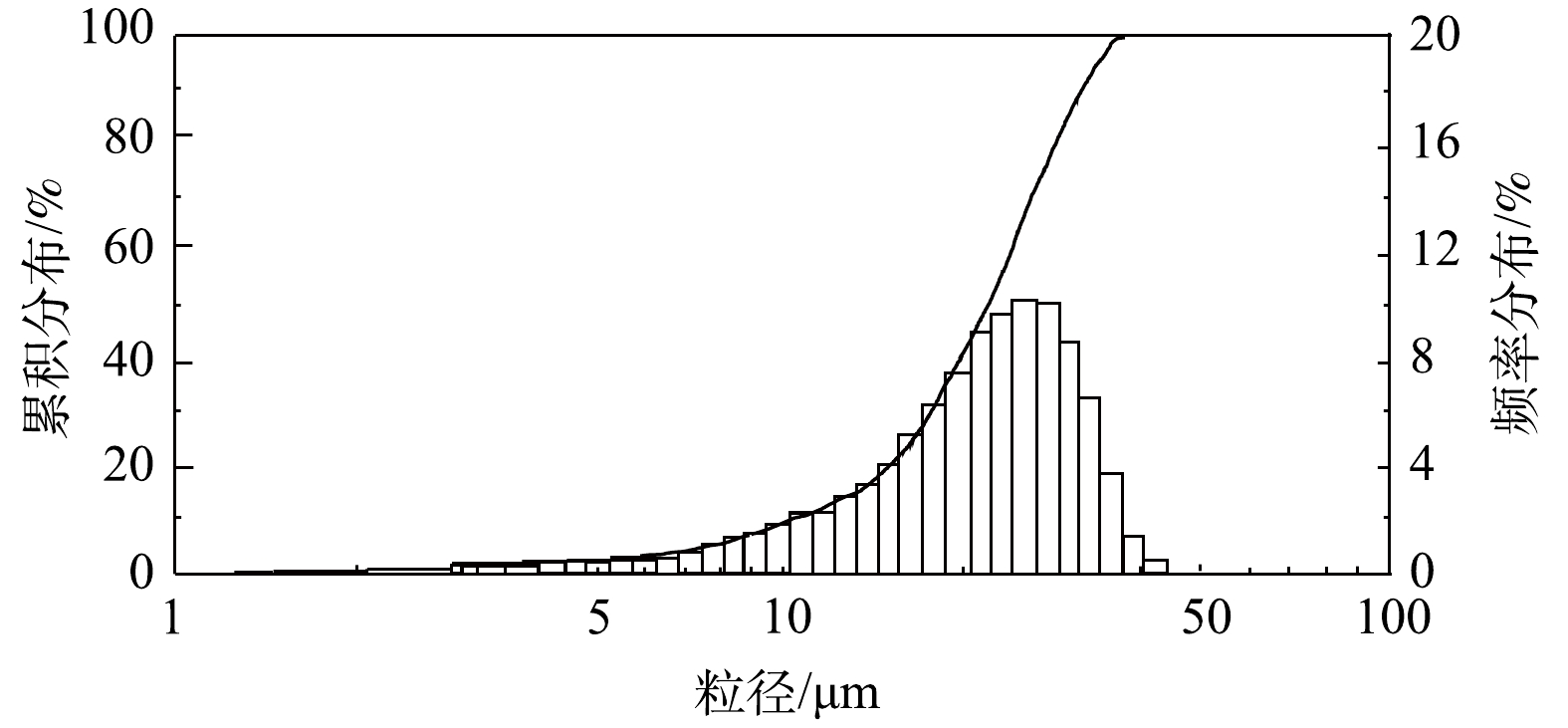
风量和旋线转速均采用变频器控制。通过调节水压改变水雾直径,采用Winner 318激光粒度分析仪测定实验水雾的粒径分布如图7所示。水雾中位径为20.1 μm,实验雾滴大小接近工业脱硫塔烟气夹带液滴的粒径范围[26]。
除雾效率的测定采用水平衡法[27]。在图6中,雾化水箱的失水量为喷嘴总喷水量m1,喷头喷出的雾化水雾随气流运动,喷到进气管壁上的雾滴汇入沉降水箱中,水量为m2。实际进入旋线除雾器筒体的总水雾量m0=m1−m2,被旋线旋线捕集的雾滴流入捕集水箱中,水量为mc,则除雾效率见式(32)。
ηT=mc/m0 (32) 2.3 实验条件
实验在常温常压下进行,双层旋线除雾器每层旋线根数分别取100根和200根。考虑到现有静电除雾器的处理风速通常不超过2 m·s−1[28],为体现旋线除雾器的优势,实验风速取2.5 m·s−1。喷嘴的喷液量为1 355 kg·h−1,水雾浓度为4 100 mg·m−3。
2.4 检验结果与讨论
2.4.1 效率理论的检验
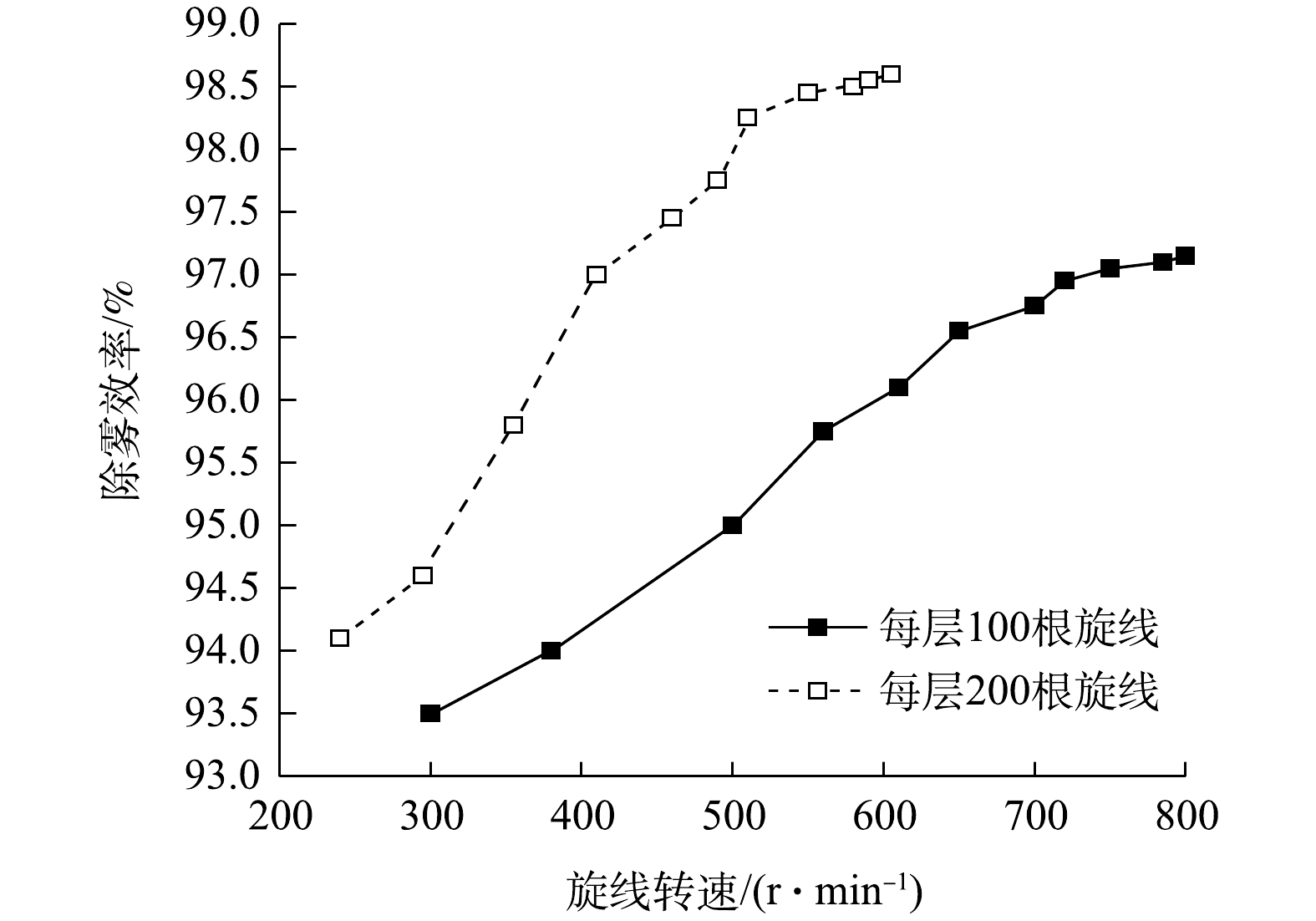
当每层旋线分别为100根和200根时,测得双层旋线除雾器的除雾效率与旋线转速的关系如图8所示。
结果表明,增加旋线根数的提效作用非常显著。采用直径3 mm旋线捕集中位径20.1 μm的水雾,当旋线转速500 r·min−1时,每层旋线为100根时除雾总效率约95%,当旋线增至每层200根时,除雾总效率为98.1%。
由于实验所测得的除雾效率是总除雾效率,所建立除雾效率理论式(31)是分级效率,二者无法比较。为将实验所得总效率与分级效率相联系以便于评价除雾器的性能,ZHAO等[29]通过大量实验数据和试错研究发现,颗粒群的总捕集效率和颗粒群中位径近似存在的关系如式(33)所示。
ηT=1−exp(−k0dp50) (33) 式中:ηT为总效率实验值;k0为待定系数;dp50为颗粒群中位径。
根据已知总效率实验值ηT和颗粒群中位径dp50,由式(33)可确定系数k0。于是,基于分级效率服从指数规律,ZHAO等[29]得出预估分级效率经验式(34)。
ηe=1−exp(−k0dp) (34) 式中:ηe为预估分级效率。
作为验证性研究,仅讨论旋线转速500 r·min−1情况下分级效率理论值与分级效率经验预估值的吻合度。
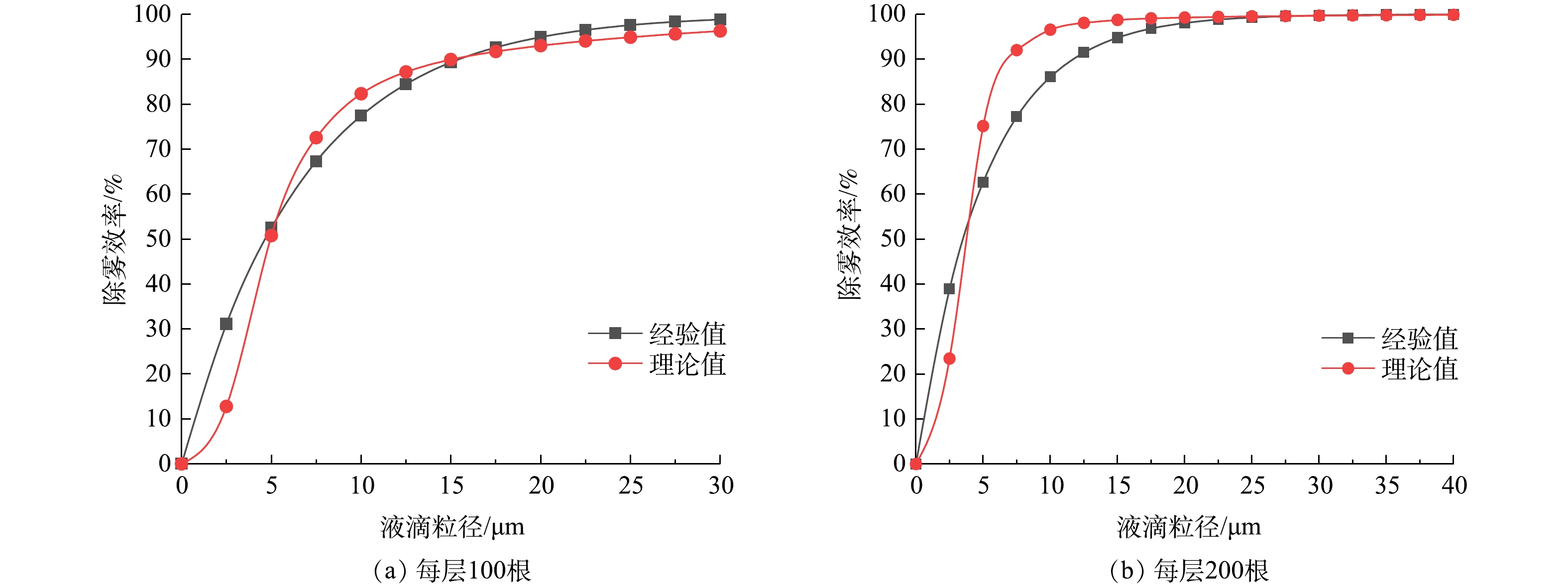
由总效率实验结果图8和式(33)得出的k0值(见表1)。由式(34)分别得出每层100根和200根时的分级效率经验值ηe,然后由式(31)得出双层旋线除雾器分级效率理论值ηC,将计算结果绘于图9中。
表 1 k0值计算表Table 1. Calculation value of k0转速n/(r·min−1) 角速度ω/(rad·s−1) 每层旋线根数 总效率实验值/% k0 500 16.7π 100 95.0 0.149 200 98.1 0.197 实验结果表明,当雾径小于5 μm,旋线除雾器分级效率理论值低于经验值;当雾径为5~20 μm时,理论值高于经验值,随后二者相互逼近。上述现象的原因是,当雾径小于5 μm,惯性碰撞效应较弱,而当雾径大于5 μm,惯性碰撞作用明显增强。总体看,旋线除雾器分级效率理论值与经验值相当吻合,在雾径为0~40 μm时,平均误差约1.4%,说明双层旋线的拦截、惯性碰撞与旋流离心分离复合除雾效率理论是比较准确的。
2.4.2 不同机理的提效作用
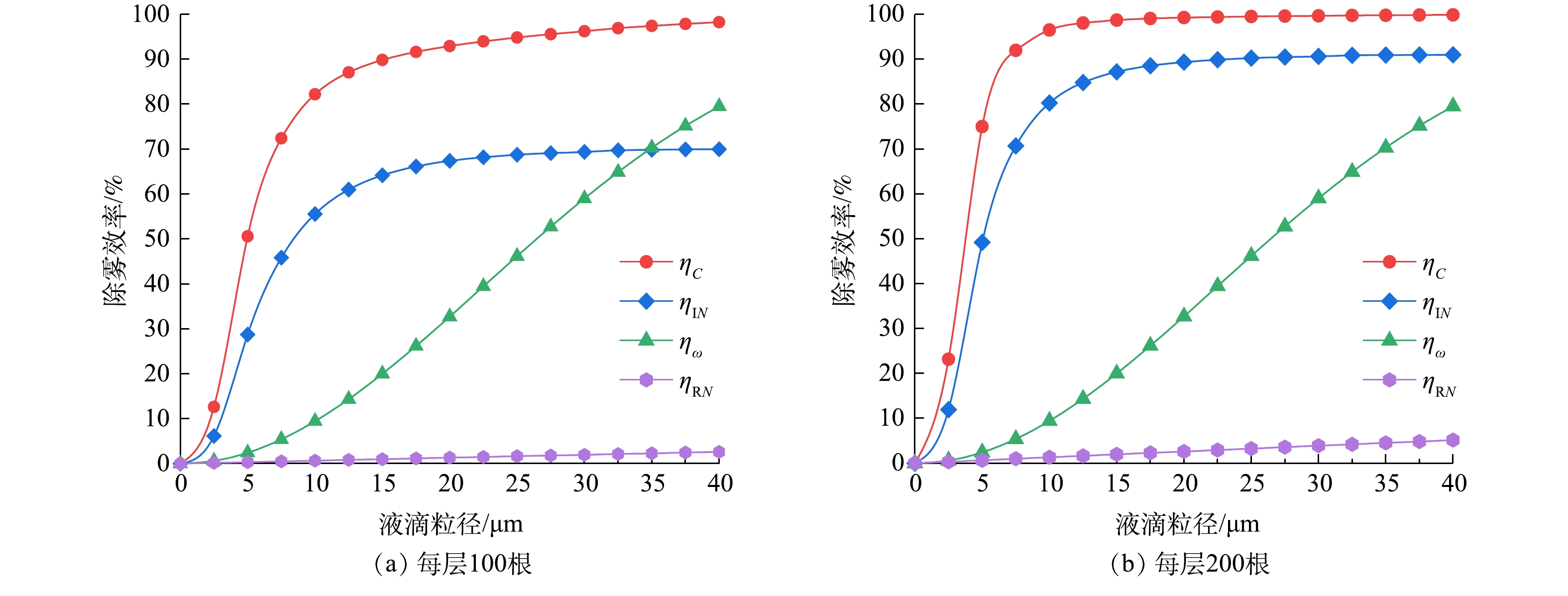
为明确各捕集机理在旋线除雾中的作用,取旋线转速500 r·min−1,将单层拦截ηRN、惯性碰撞ηIN、旋流离心分离ηω和双层复合除雾效率ηc的计算结果绘于图10中。由图10可看出,惯性碰撞效应起主导作用,旋流分离次之,拦截效率对旋线除雾器效率的贡献很小。如对20 μm雾滴,在每层旋线
N=200 3. 结论
1)旋线除雾器的除雾机理主要是拦截、惯性碰撞和旋线的高速旋转产生的旋流离心分离。理论研究表明,拦截和惯性碰撞随旋线转速和旋线根数的增加而提高,但增加旋线根数的提效作用更有效;旋流离心分离效率是雾径和转速的平方的函数,且服从指数规律。
2)双层旋线除雾器的理论分级效率的验证结果表明,在旋线转速500 r·min−1、旋线直径3 mm、每层旋线分别为100根和200根的情况下,在0~40 μm雾径范围内,旋线除雾器分级效率理论值与经验值基本吻合,平均误差约1.4%,说明双层旋线器的复合除雾效率理论是比较准确的。
3)对比各机理在旋线除雾器中的提效作用可看出,旋线的惯性碰撞效应起主导作用,特别是对小粒径的雾滴有较高的捕集效率;旋流离心分离作用次之,对于小粒径雾滴分离效率不高,但随着雾滴粒径的增加效率提升较快;旋线的拦截除雾效率较低,几乎可以忽略不计。
-
表 1 边界层条件计算表
Table 1. Calculation table of boundary layer conditions
进水口直径/m 进水口流速/m·s−1 进水口雷诺数 进水口湍流强度 0.006 1.5 8 922.38 5.13% 出水口直径/m 出水口雷诺数 出水口湍流强度 0.11 973.35 6.77% -
[1] 周文哲. 隧道施工废水处理研究[J]. 铁道建筑, 2019, 59(9): 77-80. doi: 10.3969/j.issn.1003-1995.2019.09.19 [2] 祝捷. 引汉济渭工程输水隧洞施工废水处理工艺研究[J]. 铁道工程学报, 2014, 31(6): 109-113. doi: 10.3969/j.issn.1006-2106.2014.06.022 [3] 薛正. 铁路隧道施工废水处理存在的问题[J]. 铁道建筑, 2021, 61(4): 57-61. [4] 吴楠, 王三反, 黑见星, 等. 高海拔低温地区强化混凝沉淀过滤处理隧道施工废水[J]. 中国给水排水, 2017, 33(22): 85-88. doi: 10.19853/j.zgjsps.1000-4602.2017.22.019 [5] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 污水综合排放标准: GB 8978-1996 [S]. 北京: 中国环境科学出版社, 1996. [6] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 地表水质量标准: GB 3838-2002 [S]. 北京: 中国环境科学出版社, 2002. [7] 晓溪. 旋流反应澄清池[J]. 建筑技术通讯(给水排水), 1982(4): 32-35. [8] 李国龙. 旋流式水力循环澄清池的设计和研究[J]. 建筑技术通讯(给水排水), 1981(4): 8-12+24. [9] 常青. 絮凝动力学的现状与研究方法进展[J]. 环境科学学报, 2015, 35(10): 3042-3049. doi: 10.13671/j.hjkxxb.2015.0091 [10] 贺维鹏, 曹玉烛, 施周, 等. 基于CFD的网格絮凝池内水流紊动协同效应分析[J]. 湖南师范大学自然科学学报, 2017, 40(4): 14-20. doi: 10.7612/j.issn.1000-2537.2017.04.003 [11] DAI H L, QIU Z M, HU F P, et al. Floc Performance parameters during water treatment in a micro-vortex flocculation process determined by machine vision[J]. Environmental Technology, 2019, 40(23): 3062-3071. doi: 10.1080/09593330.2018.1465127 [12] WANG X, CUI B, WEI D, et al. CFD-PBM modelling of tailings flocculation in a lab-scale gravity thickener[J]. Powder Technology, 2022, 396: 139-151. doi: 10.1016/j.powtec.2021.10.054 [13] 童祯恭, 杨静芝, 董红军. 涡流澄清池反应区流态模拟及试验分析[J]. 环境科学与技术, 2013, 36(11): 112-116. [14] 王艺, 戴红玲, 周政, 等. 微涡流絮凝工艺处理低温低浊微污染水的优化[J]. 中国给水排水, 2019, 35(23): 41-47+52. doi: 10.19853/j.zgjsps.1000-4602.2019.23.008 [15] 何亚其, 白健华, 孙超, 等. 新型微涡流混凝器絮凝效果评价及数值模拟分析[J]. 工业水处理, 2021, 41(6): 206-210. doi: 10.11894/iwt.2020-0868 [16] 祝威, 王志新, 韩霞, 等. 气携式涡旋絮凝反应器数值模拟[J]. 中国矿业大学学报, 2019, 48(4): 911-918. doi: 10.13247/j.cnki.jcumt.001039 [17] BRIDGEMAN J, JEFFERSON B, PARSONS S. The development and application of CFD models for water treatment flocculators[J]. Advances in Engineering Software, 2010, 41(1): 99-109. doi: 10.1016/j.advengsoft.2008.12.007 [18] 王福军. 计算流体动力学分析[M]. 清华大学出版社, 2004. [19] LIANO CE, CORAL JA, FONTALVO J, et al. CFD assisted analysis and design of hydraulic flocculators[J]. Revista Mexicana de Ingenieria Quimica, 2019, 18(3): 995-1015. doi: 10.24275/uam/izt/dcbi/revmexingquim/2019v18n3/Llano [20] BRIDGEMAN J, JEFFERSON B, PARSONS S. Assessing floc strength using CFD to improve organics removal[J]. Chemical Engineering Research & Design, 2008, 86(8): 941-950. [21] OYEGBILE B, AKDOGAN G, KARIMI M. Experimental and CFD studies of the hydrodynamics in wet agglomeration process[J]. Chem Engineering, 2018, 2(3): 32-49. [22] 李圣洁. 网格板几何尺寸对网格絮凝池流场影响的数值模拟研究[D]. 兰州交通大学. [23] ZHAN M, YOU M, LIU L, et al. Numerical simulation of mechanical flocculation in water treatment[J]. Journal of Environmental Chemical Engineering, 2021, 9(4): 105536. doi: 10.1016/j.jece.2021.105536 [24] 赫俊国, 赵连栋, 宋宏伟. 涡旋混凝低脉动沉淀技术在海港水厂的应用[J]. 给水排水, 2002, 28(1): 42-45. doi: 10.3969/j.issn.1002-8471.2002.01.013 [25] 张鹏天, 胡锋平, 张琪, 等. 涡流反应器及其在即墨市南水厂的应用[J]. 华东交通大学学报, 2006(5): 9-11. doi: 10.3969/j.issn.1005-0523.2006.05.003 [26] LU S, DING Y, GUO J. Kinetics of fine particle aggregation in turbulence[J]. ADVANCES IN COLLOID AND INTERFACE SCIENCE, 1998, 78(3): 197-235. doi: 10.1016/S0001-8686(98)00062-1 [27] FAN W B, LI W G, GOMG X J, et al. Evaluation of the effect of a hydraulic impeller in a flocculation basin on hydrodynamic behavior using computational fluid dynamics[J]. Desalination & Water Treatment, 2015, 54(4-5): 1361-1374. [28] DSDO A, CBD B. Global velocity gradient evaluation: An innovative approach using CFD modeling applied to water and wastewater treatment plants[J]. Journal of Water Process Engineering, 2019, 28(C): 21-27. [29] 王绍文. 惯性效应在絮凝中的动力学作用[J]. 中国给水排水, 1998, 14(2): 13-15. doi: 10.3321/j.issn:1000-4602.1998.02.004 [30] WATANABE Y. Flocculation and me[J]. Water Research, 2017, 114(1): 88-103. [31] COSTINE A, COX J, TRAVAGLINI S, et. al. Variations in the molecular weight response of anionic polyacrylamides under different flocculation conditions[J]. Chemical Engineering Science, 2018, 176: 127-138. doi: 10.1016/j.ces.2017.10.031 [32] 卢佳, 王毅力, 杜白雨, 等. 聚合氯化铁-腐殖酸(PFC-HA)絮体的粒度和分形维数的动态变化[J]. 环境科学学报, 2008, 28(4): 624-633. doi: 10.3321/j.issn:0253-2468.2008.04.005 [33] 金鹏康, 王晓昌. 腐殖酸絮凝体的形态学特征和混凝化学条件[J]. 腐植酸, 2008(1): 39-39+2. doi: 10.19451/j.cnki.issn1671-9212.2008.01.012 [34] 柴宝红, 方布雷, 王岩, 等. 隧道废水小粒径悬浮物微絮凝法快速处理技术[J]. 隧道与地下工程灾害防治, 2021, 3(4): 61-67. doi: 10.19952/j.cnki.2096-5052.2021.04.07 [35] 史志皓, 朱海涛, 欧阳卓明, 等. 武汉市汉江原水悬浮物浓度与浊度对应关系的研究[J]. 中国给水排水, 2022, 38(21): 51-56. doi: 10.19853/j.zgjsps.1000-4602.2022.21.007 [36] 曹赞. 基于Fluent的微涡流絮凝工艺数值模拟与关键运行参数优化[D]. 华东交通大学, 2019. [37] 张兆顺, 崔桂香, 许春晓. 湍流理论与模拟[M]. 湍流理论与模拟, 2005. 期刊类型引用(1)
1. 祝雄涛,李德良,于洋. 小型水厂星伞絮凝/浮沉/过滤一体化工艺设计与运行. 中国给水排水. 2024(24): 53-58 .  百度学术
百度学术
其他类型引用(1)
-






 下载:
下载: