-
钢铁行业能源消耗巨大,在钢铁加工制造过程中会产生大量颗粒物[1-3]。我国日益提高的环境标准,为颗粒物的有效处理提出了新的要求[4]。目前,纤维捕集技术是最有效的颗粒物处理手段之一,被广泛应用在工业中[5]。Davies孤立圆柱理论是纤维捕集颗粒物理论的基础[6]。随着工业技术的进步,纤维截面的形状已经产生了2类变化:截面形状的非圆化,包括截面形状轮廓波动的异形化和截面直径不对称的异形化;截面的中空和复合化[7]。纤维截面形状的变化使得纤维捕集颗粒物的效率也得以提升。
针对不同截面形状的颗粒物捕集纤维,国内外学者进行了相关研究。孙熙等[8]通过数值分析的方法求解矩形纤维阻力,并分析了纤维层流场的特征,结果与理论求解结果相符合。王浩明等[9]通过使用格子Boltzmann法模拟了椭圆纤维捕集颗粒物的过程,发现相同体积分数下,椭圆纤维可有效提高扩散机制为主导的颗粒物捕集效率,而拦截机制或惯性碰撞机制为主导时的捕集效率与纤维放置方式有关。顾丛汇等[10]结合欧拉-拉格朗日法对“Y”形截面和圆形截面的单纤维进行了模拟,发现“Y”形纤维对颗粒物的截留效率高于圆形纤维。王坤等[11]使用格子Boltzmann法模拟了三角形、十字形及三叶形3种异形纤维捕集颗粒物的过程,发现扩散机制主导时捕集效率不受纤维放置方式影响,拦截机制和惯性机制主导时捕集效率均受纤维放置方式影响。杨会等[12]采用数值方法求解绕方形纤维截面纤维流场,考虑了布朗扩散、拦截效率和惯性碰撞3种捕集机理的联合作用,研究了方形截面纤维的过滤性能,发现方形纤维对以扩散捕集机制为主的小粒子和惯性捕集机制的大粒子在纤维表面表现出显著的局部沉积特征,并与方形纤维的迎风角度有关,而方形截面纤维对颗粒物的捕集性能与填充率有关。RAYNOR[13]通过数值计算的方法求解了椭圆纤维表面的流动特征并与理论计算结果进行了对比,验证了数值计算的可靠性。HOSSEINI等[14]模拟了圆形纤维、方形纤维、椭圆形纤维和三叶形纤维4种截面形状纤维结构,并考虑了纳米纤维表面的滑移效应,对比分析了4种截面形状纤维捕集颗粒物的性能,结果表明,纤维形状对纳米纤维性能的影响大于微米级纤维。FOTOVATI等[15]模拟研究了三叶形纤维捕集颗粒物的性能,得出了三叶形纤维捕集效率与三叶形纤维内切圆和外接圆之比的关系。SALEH等[16]的模拟研究表明,三叶形纤维的捕集效率和颗粒物在纤维表面的沉积特性受其纤维放置方式的影响较明显。HUANG等[17]模拟了长方形、三叶形、四叶形和三角形4种异形纤维的颗粒物捕集效率,发现异形纤维对亚微米颗粒物的捕集效率更高。HUANG等[18]发现,颗粒物会在椭圆形纤维表面均匀沉积,并最终形成树枝状结构。
现有对不同横截面形状纤维的研究,多集中在单一横截面形状。为了探究横截面形状多角形变化方式对纤维捕集颗粒物性能的影响,有必要对横截面形状为正多边形的异形纤维进行模拟研究。目前,计算流体力学(computational fluid dynamics, CFD)发展迅速,Fluent是目前比较常见的商用CFD软件包,可用来模拟流体[19]、热传递[20]及化学反应[21]等,其中内置的离散相模型(discrete phase model, DPM)在拉格朗日坐标系下求解颗粒物微分方程,并计算离散相的颗粒轨道,经常用于模拟颗粒物捕集与沉积[22]、液滴的干燥[23]、颗粒燃烧[24]等。
本研究从横截面为正多边形的纤维入手,探究纤维截面形状变化对单纤维捕集颗粒物效率的影响,从颗粒物粒径、入口风速、填充率和纤维放置方式等方面考察了不同横截面形状纤维捕集颗粒物的性能,为纤维的优化设计提供参考,以提高异形纤维对颗粒物的捕集效率。
-
对于内部气-固两相流动进行模拟需要先计算气相场。文中采用层流(Laminar)、稳态(Steady)及不可压缩模型进行数值模拟。控制方程[25](连续性方程、动量方程)见式(1)和式(2)。
式中:v为流体的速度,m·s−1;µ为流体的动力黏度, Pa·s;p为计算单元的压力,N。
采用二阶迎风格式SIMPLE算法对离散化动量方程进行压力速度耦合求解,并将各项收敛残差均设定在10−6。颗粒物采用面(surface)注入的方式进入流场,注入的颗粒总数为5 000个。假定颗粒物在流场中作无旋运动。颗粒物采用标准球形颗粒,粒径为0.5~2.5 μm。假设只考虑曳力和重力,而忽略了其他力的作用,颗粒物的受力平衡方程[25]见式(3)。
式中:g为重力加速度,m·s−2:ρ为流体密度,kg·m−3:Fother为颗粒物运动过程所受其他可以忽略的力,N。
-
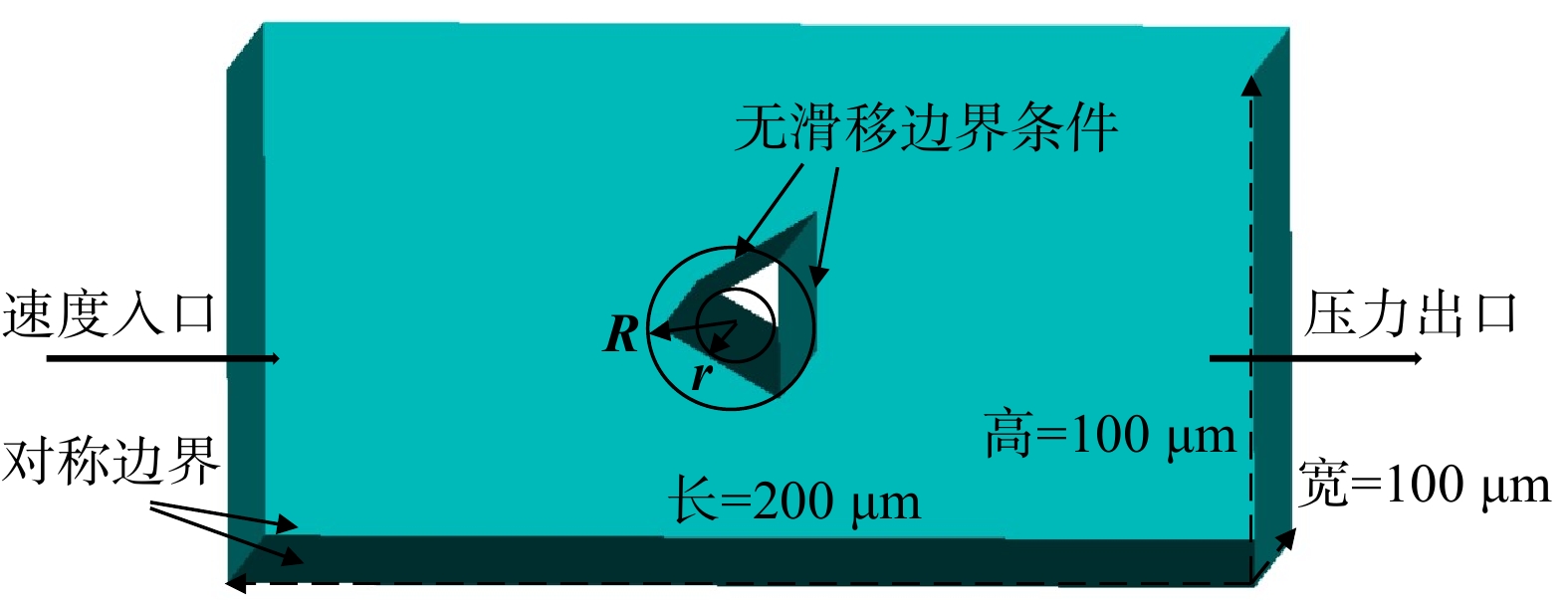
为考察异形纤维的颗粒物捕集性能,建立了不同横截面形状的纤维模型。计算域(Domain)入口处设置为速度入口边界条件(Velocity-inlet),出口设置为压力出口(Pressure-outlet),四周壁面设置为对称边界(Symmetry),如图1所示。以直径为20 µm的圆柱形纤维为标准,保证其相同的横截面积,建立了横截面为正多边形的异形纤维模型,如图2所示。纤维的放置方式分为2种:1)异形纤维的角平分线与气流方向平行,异形纤维的边线与气流方向呈钝角,如图3(a);2)异形纤维的边垂线与气流方向平行,异形纤维的边线与气流方向垂直,如图3(b)。由于所采用的纤维直径远大于空气分子的平均自由程,纤维表面不会发生滑移现象,故纤维表面采用无滑移壁面条件(No-slip boundary condition),计算域的长(L)、宽(W)、高(H)分别为200 µm、100 µm、100 µm。
对于纤维截面的轮廓波动异形,采用纤维的径向异形度、截面异形度和圆周系数3个无量纲参数来表示纤维截面形状的变化[7],计算式为式(4)~(6)。
式中:Dr为纤维径向异形度;R为最多接触点的外接圆半径,m;r为内切圆半径,m;Sr为纤维截面异形度;H为纤维周长系数;L为纤维截面的周长,m;S为纤维的实际截面积,m2。经计算,常见的几种不同几何截面纤维的径向异形度、截面异形度和形状系数如表1 所示。
-
为去除网格因素对模拟结果的影响,对所使用的模型网格进行了独立性检验。对于低雷诺数不压缩黏性流体来说,气体在过滤器中的流动应当满足Darcy方程[26](式(7))。多纤维系统的压降与入口速度之比为一个常数,通常把这一比值认定为纤维所受曳力。KUWABARA[27]和HAPPEL[28]分别给出无量纲曳力与纤维层填充率的关系式,如式(8)和式(9)所示。
式中:F1为Darcy方程给出的无量纲曳力表达式[26];F2为KUWABARA[27]提出的无量纲曳力关于纤维层填充率α的表达式;F3为HAPPEL[28]给出的纤维层流动时的无量纲曳力关于纤维层填充率α的表达式;Z为纤维层厚度, m;α为纤维层的体积分数[27],α= d2f·H−2;df为纤维直径, m;Δp为纤维层实际压降, Pa。
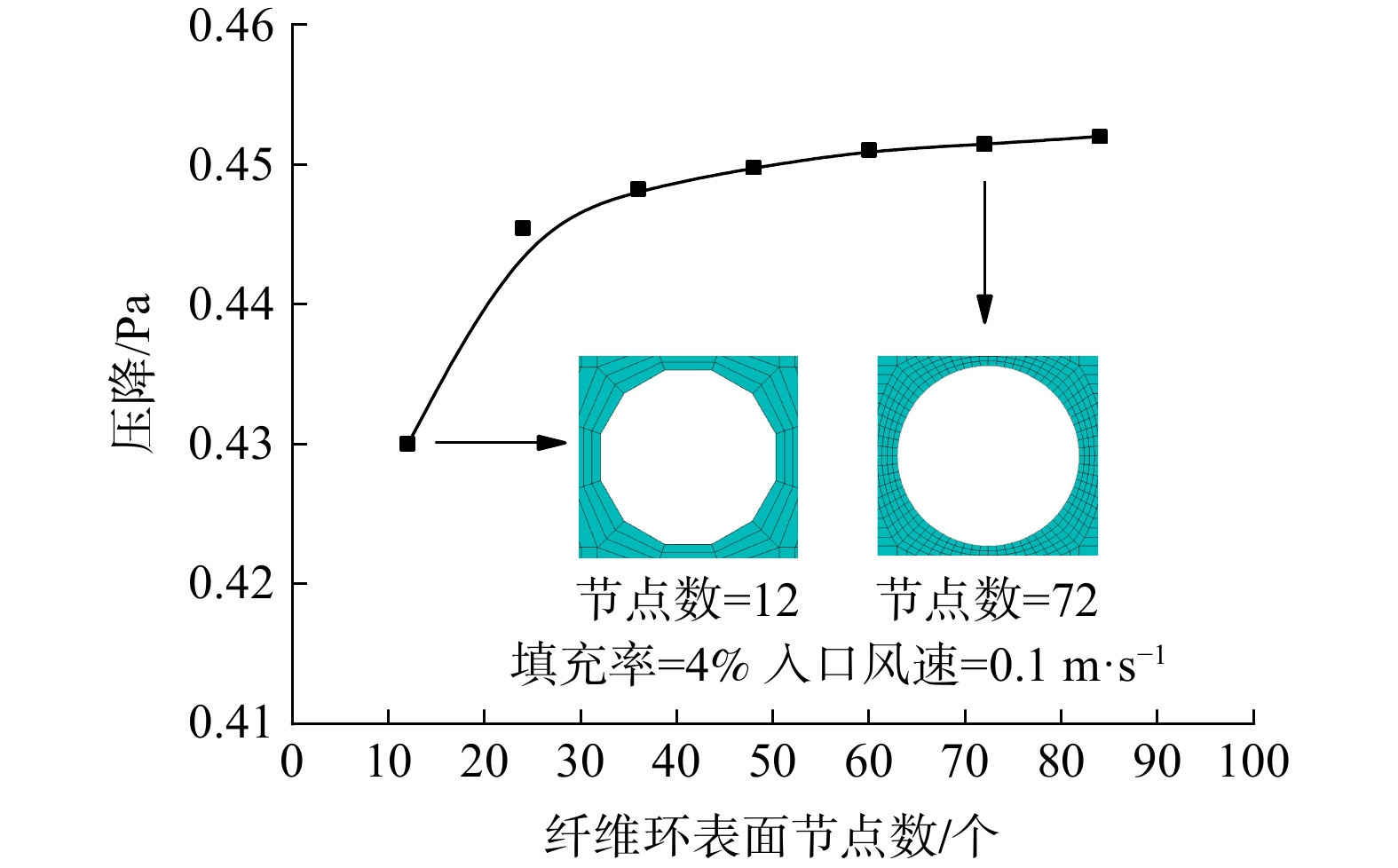
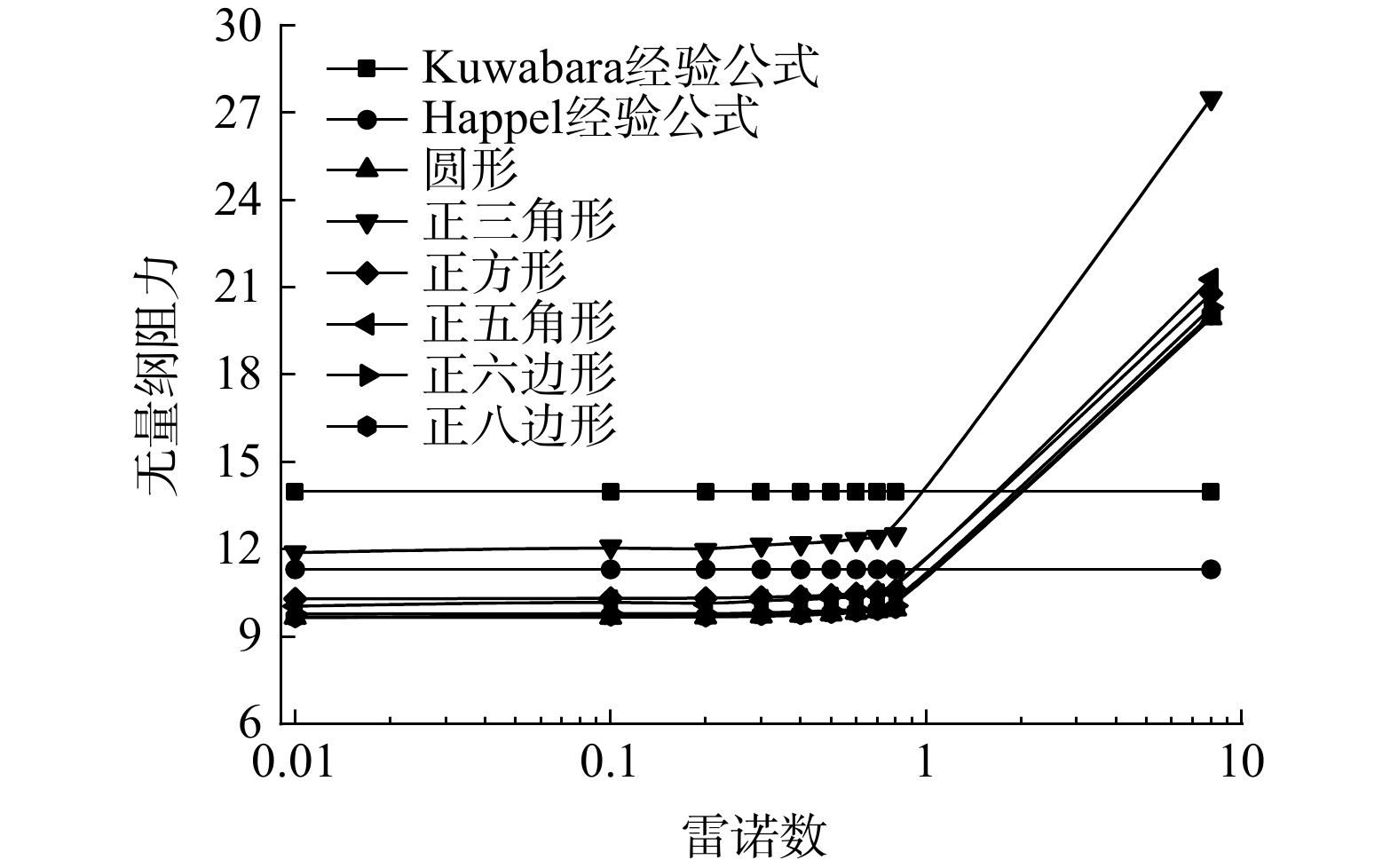
LIU等[29]进一步研究后发现,纤维的雷诺数(Re=ρvdf/μ)等于1时是纤维压力损失一个重要节点。当Re数大于1时,F1值开始随Re数升高而升高;Re数小于1时,F1值为定常数,模拟结果应符合此规律。图4为圆形单纤维压力损失变化与纤维环网格结点数变化之间的关系。纤维的填充率为4%,入口风速为0.1 m∙s−1,纤维表面结点总数从12个增加到84个纤维表面结点总数大于等于60时,纤维的压力损失趋于稳定。本研究所建立的异形纤维模型的表面网格密度均与圆形单纤维表面网格密度相同。所有网格均采用六面体结构化网格,并对纤维表面部分进行加密处理,网格质量均大于0.7。图5为数值模拟结果与经验公式对比图,网格质量符合数值模拟要求,因此,文中所采用的网格可准确表示纤维表面的流动特点。
为验证纤维对颗粒物捕集效率的准确性,计算了单纤维模型捕集颗粒物的效率,并与经验公式进行了对比。不考虑布朗运动时,单纤维的捕集效率有多种计算方式。式(10)、(11)分别为Davies经验公式[6]及其修正式。由于本研究没有考虑布朗力的作用,故忽略布朗力作用下,单纤维对颗粒物的捕集效率也可用式(12)表示[30]。
式中:η为纤维捕集效率,%;Rp为直接碰撞系数;St为斯托克斯数;η0为修正后单纤维的捕集效率,%;ηt为单纤维在惯性碰撞和拦截机制下的总捕集效率,%;ER为单纤维的拦截捕集效率,%;EI为单纤维惯性碰撞捕集效率,%。模拟结果采用式(15)进行计算[31]。图6表明,横截面为圆形的单纤维在填充率为4%时,模拟结果与经验公式相近,在误差允许范围内。
-
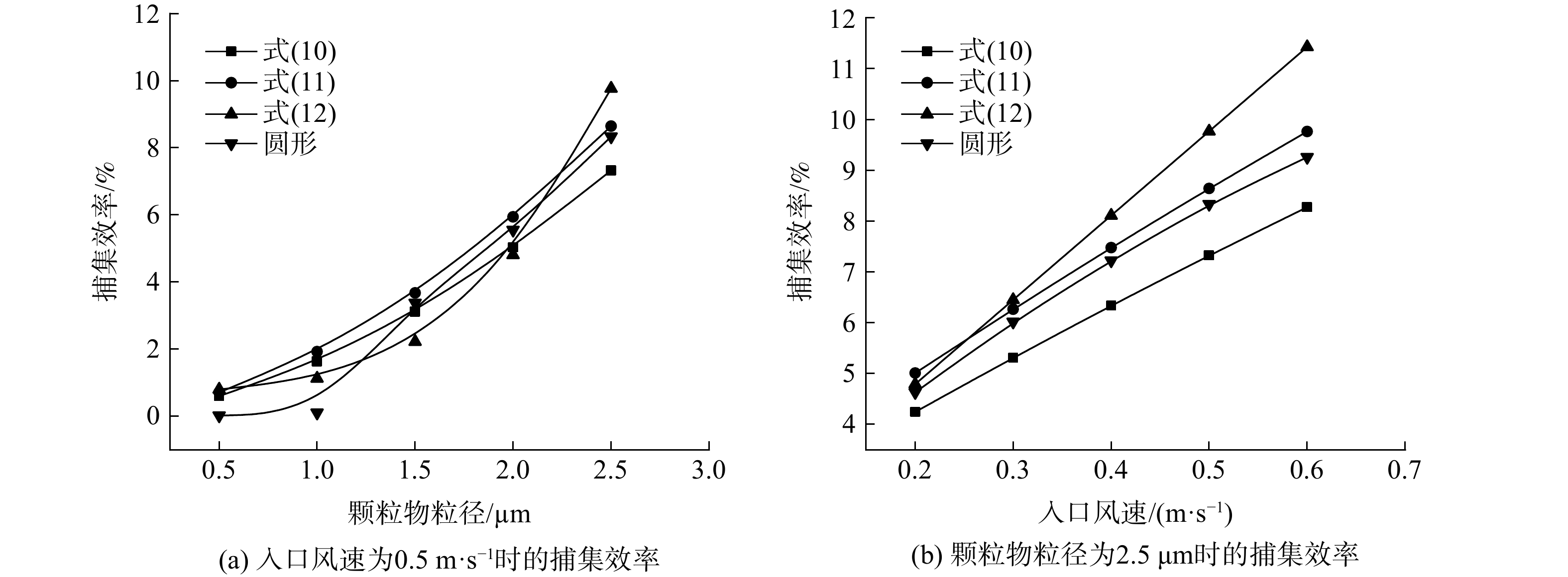
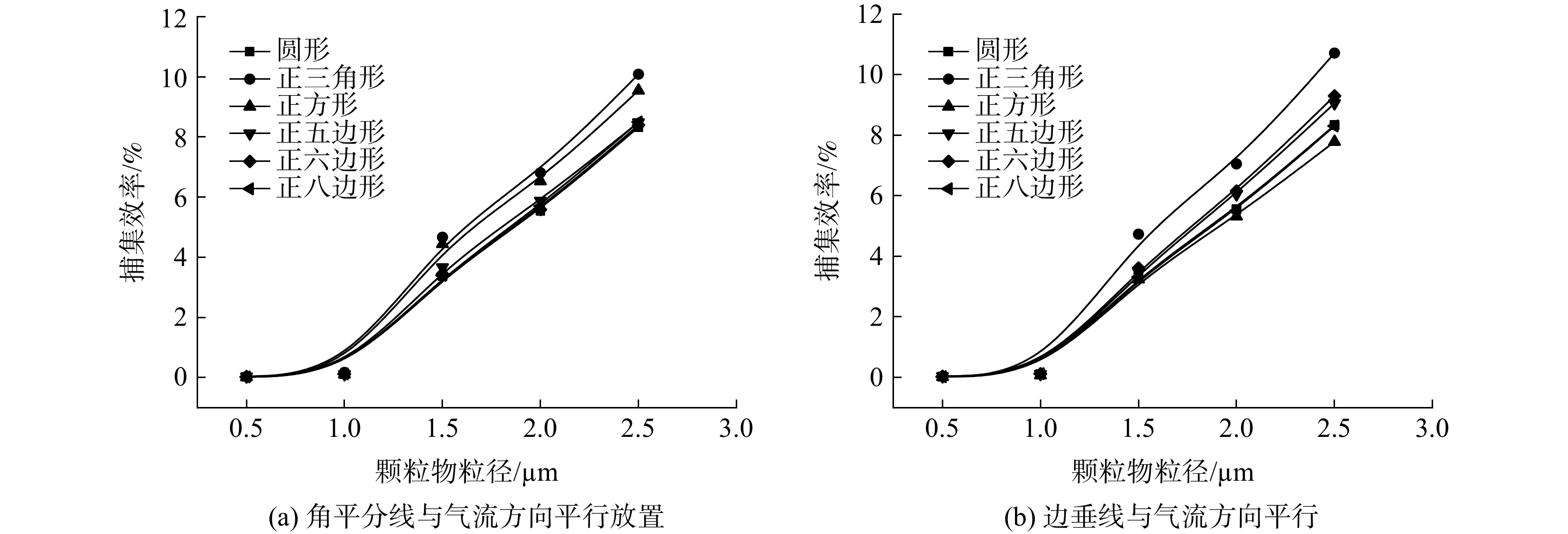
图7 为不同异形纤维在填充率为4%、入口风速为0.5 m·s−1时,对粒径为0.5~2.5 μm颗粒物的捕集效率。由图7可知,捕集效率随颗粒物粒径的增加而增加。图7(a)中异形纤维的放置方式同图3(a),与横截面形状为圆形的纤维相比,三角形纤维和四边形纤维均有效提高了单纤维对粒径为1.5~2.5 μm颗粒物的捕集效率。其中,三角形纤维的捕集效率最大。图7(b)中异形纤维的放置方式同图3(b),只有三角形纤维有效提高了单纤维对粒径为1.5~2.5 μm颗粒物的捕集效率。这是因为:纤维的外接圆直径增加,导致直接碰撞系数增加,拦截机制下的捕集效率相应增加,同时气流绕柱流动的轨迹发生改变,从而提高了惯性碰撞机制下的捕集效率。
对比2种放置方式下异形纤维对颗粒物的捕集效率,发现三角形纤维和正五边形纤维在捕集粒径为1.5~2.5 μm的颗粒物时,以图3(a)方式放置的捕集效率高于以图3(b)方式放置的捕集效率。其中,方形纤维对颗粒物的捕集效率受纤维放置方式影响最大。这是由于:2种放置方式影响了方形纤维迎风横截面积的大小,故方形纤维的捕集效率受放置方式的影响最大。异形纤维对粒径为0.5~1.0 μm的颗粒物捕集效率没有明显提高。这是因为拦截和惯性碰撞2种捕集机制对小粒径颗粒的作用不明显,所以其捕集效率没有明显增加。
-
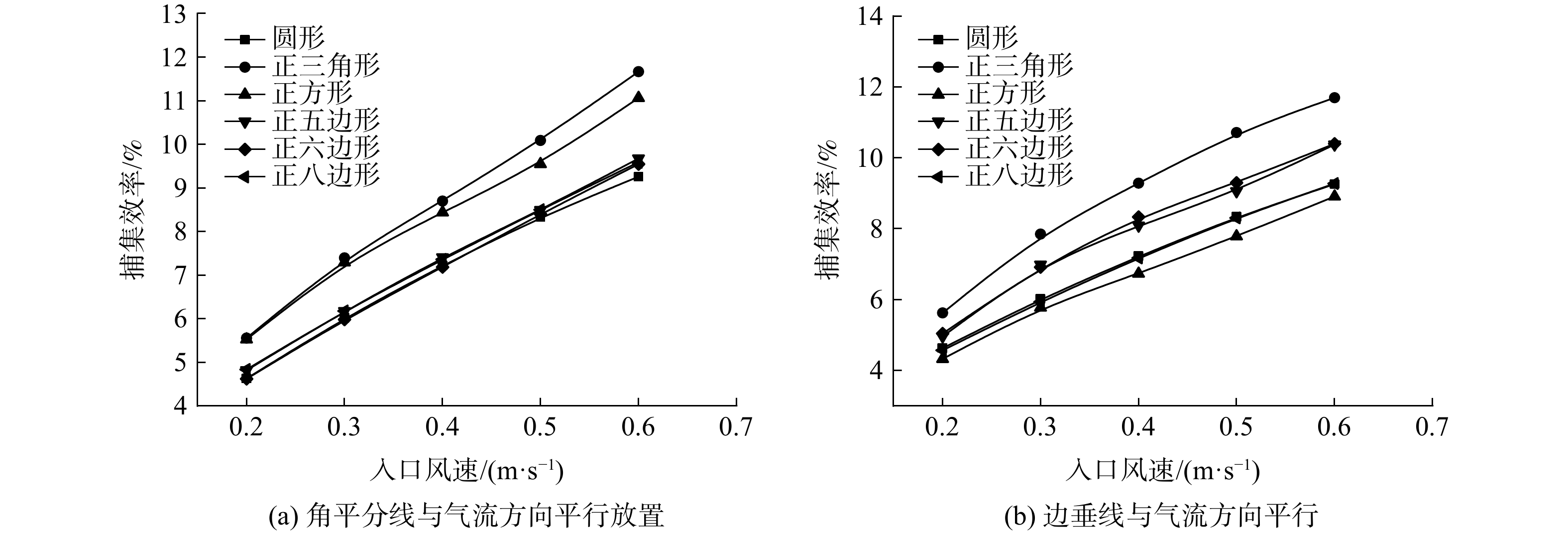
图8 是填充率为4%、颗粒物粒径为2.5 μm,入口风速为0.2~0.6 m·s−1时,不同异形纤维对颗粒物的捕集效率。可以看出,异形纤维对颗粒物的捕集效率随入口风速的增加而增加。图8(a)中异形纤维以图3(a)方式放置,与横截面为圆形的纤维相比,三角形和方形纤维在不同风速下对粒径为2.5 μm颗粒物的捕集效率均有提升。图8(b)中异形纤维以图3(b)方式放置。与圆形纤维相比,在不同风速下,三角形纤维、五边形纤维和六边形纤维对粒径为2.5 μm颗粒物的捕集效率均有提高 。这是因为:入口风速增加时,虽然直接碰撞系数不变,但颗粒物的斯托克斯数增加,导致惯性碰撞机制的捕集效率增加,故纤维的捕集效率增加。三角形和五边形纤维在入口风速为0.2~0.6 m·s−1,捕集粒径为2.5 μm的颗粒物时,以图3(a)方式放置的异形纤维对颗粒物的捕集效率高于以图3(b)方向方式放置的异形纤维。这是因为纤维截面形状对气流绕柱流动轨迹的改变会导致惯性碰撞机制捕集效率产生差异,纤维的捕集效率亦会产生差异。六边形和八边形纤维对颗粒物的捕集效率与圆形纤维相比,没有明显提高。
-
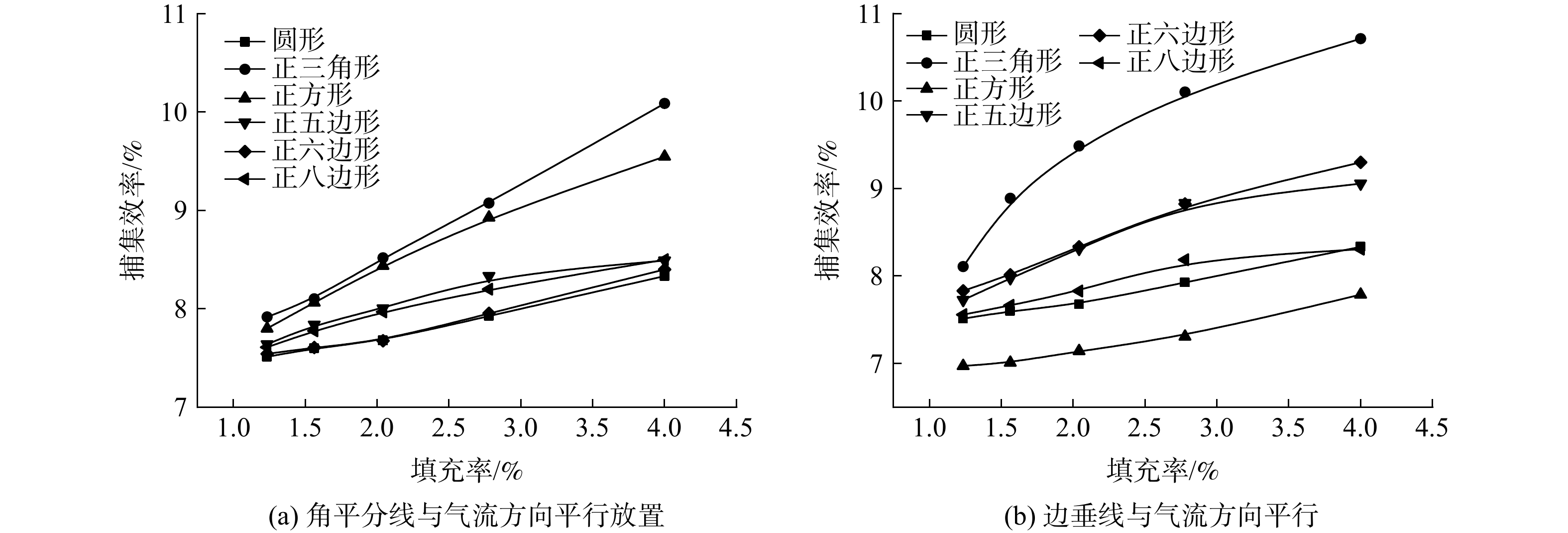
图9为异形纤维在填充率为1.2%~4.0%时,对入口风速为0.5 m·s−1的粒径为2.5 μm颗粒物的捕集效率。该图表明,异形纤维对颗粒物的捕集效率随填充率增加而增加。图9(a)中异形纤维以图3(a)的方式放置,与横截面为圆形的纤维相比,三角形纤维和方形纤维有效提高了纤维对粒径2.5 μm颗粒的捕集效率。图9(b)中异形纤维以图3(b)方式放置,与圆形纤维相比,三角形纤维有效提高了纤维对粒径为2.5 μm颗粒的捕集效率。五边形纤维和六边形纤维捕集颗粒物的效率均高于圆形纤维,但低于三角形纤维。
-
1)增加颗粒物粒径、提高入口风速和增加纤维填充率3种方式均能有效提高圆形纤维和异形纤维对颗粒物的捕集效率。三角形纤维在2种放置方式下,对颗粒物捕集效率最高,正八边形纤维的捕集效率在2种放置方式下均与圆形纤维相近。
2)异形纤维对颗粒物的捕集效率受放置方式的影响,对于相同迎风横截面积的异形纤维,以异形纤维边的中点与形心连线方式放置的异形纤维对颗粒物的撑捕集效率大于以顶角与形心连线的捕集效率。因此,相同迎风截面的异形纤维应采用边迎风的方式来提高异形纤维对颗粒物的捕集效率。
3)不同放置方式的异形纤维对颗粒物捕集性能受异形纤维径向异形度的影响,径向异形度越小,异形纤维对颗粒物的捕集效率越低,且受放置方式的影响也越小,其中方形纤维对颗粒物的捕集效率受放置方式影响最大。
不同横截面形状异形纤维捕集颗粒物的数值模拟
Numerical simulation for particles captured by shaped fiber with different cross-section
-
摘要: 基于离散相模型(DPM),模拟研究了不同横截面形状异形纤维在拦截和惯性碰撞2种机制下对颗粒物的捕集效率;考察了颗粒物粒径、入口风速、纤维填充率和纤维放置方式对不同横截面形状异形纤维捕集颗粒物效率的影响。结果表明,当颗粒物粒径为0.5~2.5 μm,入口风速为0.5 m·s−1时,异形纤维对颗粒物的捕集效率随粒径的增加而增加,对粒径为1.5 μm及以上颗粒物的捕集效率明显增加;入口风速为0.2~0.6 m·s−1时,颗粒物粒径为2.5 μm时,异形纤维对颗粒物的捕集效率均随入口风速的增加而增加;当填充率为1.2%~4.0%时,颗粒物粒径为2.5 μm时,异形纤维对颗粒物的捕集效率随填充率的增加而增加,其中横截面为正三角形的纤维对颗粒物的捕集效率均最大。异形纤维的径向异形度相同时,纤维边垂线与来流方向平行的放置方式对颗粒物的捕集效率较高。不同横截面形状异形纤维的径向异形度系数越小,对颗粒物的捕集效率受纤维的放置方式的影响越小。本研究可为新型纤维滤料的开发提供参考。Abstract: The research was conducted to study the efficiency of particulate matter captured by shaped fibers with different cross-section, based on the discrete phase model(DPM). The capture efficiency of particulate matter was simulated in two trapping mechanisms of the interception and inertial impaction for shaped fiber with different cross-section. The impacts of particle size, inlet velocity, fiber filling rate, and fiber placement were investigated on particulate matter capture efficiency for shaped fiber with different cross-section. The results showed that the capture efficiency of shaped fibers was increased with particle size, when particle size was 0.5~2.5 μm and inlet wind speed was 0.5 m·s-1. The capture efficiency greatly increased for particulate matter larger than 1.5 μm. When inlet velocity was 0.2~0.6 m·s-1 and particle size was 2.5 μm, the particle capture efficiency of shaped fibers was increased with inlet velocity. When the filling rate was 1.2%~4.0% and particle size was 2.5 μm, the particle capture efficiency of shaped fibers was increased with filling rate. The highest capture efficiency was achieved in the case of shaped fibers with cross-section of equilateral triangle. With the same radial deformity, the capture efficiency is higher when the edge perpendicular of the shaped fiber is parallel to the airflow direction. The impact of fiber placement on the particle capture efficiency was reduced with a smaller radial distortion coefficient of shaped fibers. The outcome of this study could inspire the fabrication of new fiber filter materials.
-
Key words:
- shaped fiber /
- numerical simulation /
- capture efficiency /
- radial irregularity
-
烟气经湿法脱硫后会产生大量含可溶性物质的白色水雾[1],导致环境污染[2]。除雾方法主要是加装除雾器[3],如折流板除雾器[4]、丝网除雾器[5]、静电除雾器等[6]。为提高除雾器的气液分离作用,NARIMANI 等[7]运用CFD的方法优化了带倒钩的折流板除雾器结构;EL-DESSOUKY 等[8]研究了不同网层厚度下丝网除雾器的最佳过滤风速;袁惠新等[9]研究了旋风除雾器在引入静电场后对细水雾的脱除效果。然而,目前水雾排放浓度依然难以达到相关标准规定的排放限值[10]。因此,白色烟羽排放的有效控制已成为湿烟气深度净化的一个研究热点[11-12]。
烟气“脱白”技术鲜有突破,其原因是除雾工程应用限制了2个高效技术路径:要求成本低、能耗少、占地小,不宜采用湿电;要求压损小、无堵塞,不能采用过滤。因此,近年来利用空气动力分离的技术方法倍受关注[13-15]。然而,采用空气动力分离除雾,需要在细而长的螺旋管中带动整个气流高速旋转,导致能耗过高,而且细水雾易被高速气流带出除雾器。
为实现高湿烟气的高效除雾,笔者提出了自由旋线除雾方法[16-17],并开展了单层自由旋线除雾实验研究[18]。结果表明,自由旋线除雾器的压损小、效率高,并且发现在控制能耗情况下增加旋线根数比增加旋线转速的提效作用更显著。然而,关于自由旋线除雾器的除雾性能还缺乏基础理论研究。本研究将基于经典的单根柱状纤维捕集和旋流离心分离机理,建立自由旋线除雾器的除雾效率理论,并通过实验加以验证,进而揭示旋线根数和转速对自由旋线除雾作用的影响规律,以期为自由旋线除雾技术的发展及应用提供参考。
1. 旋线除雾理论
1.1 旋线除雾器的工作原理
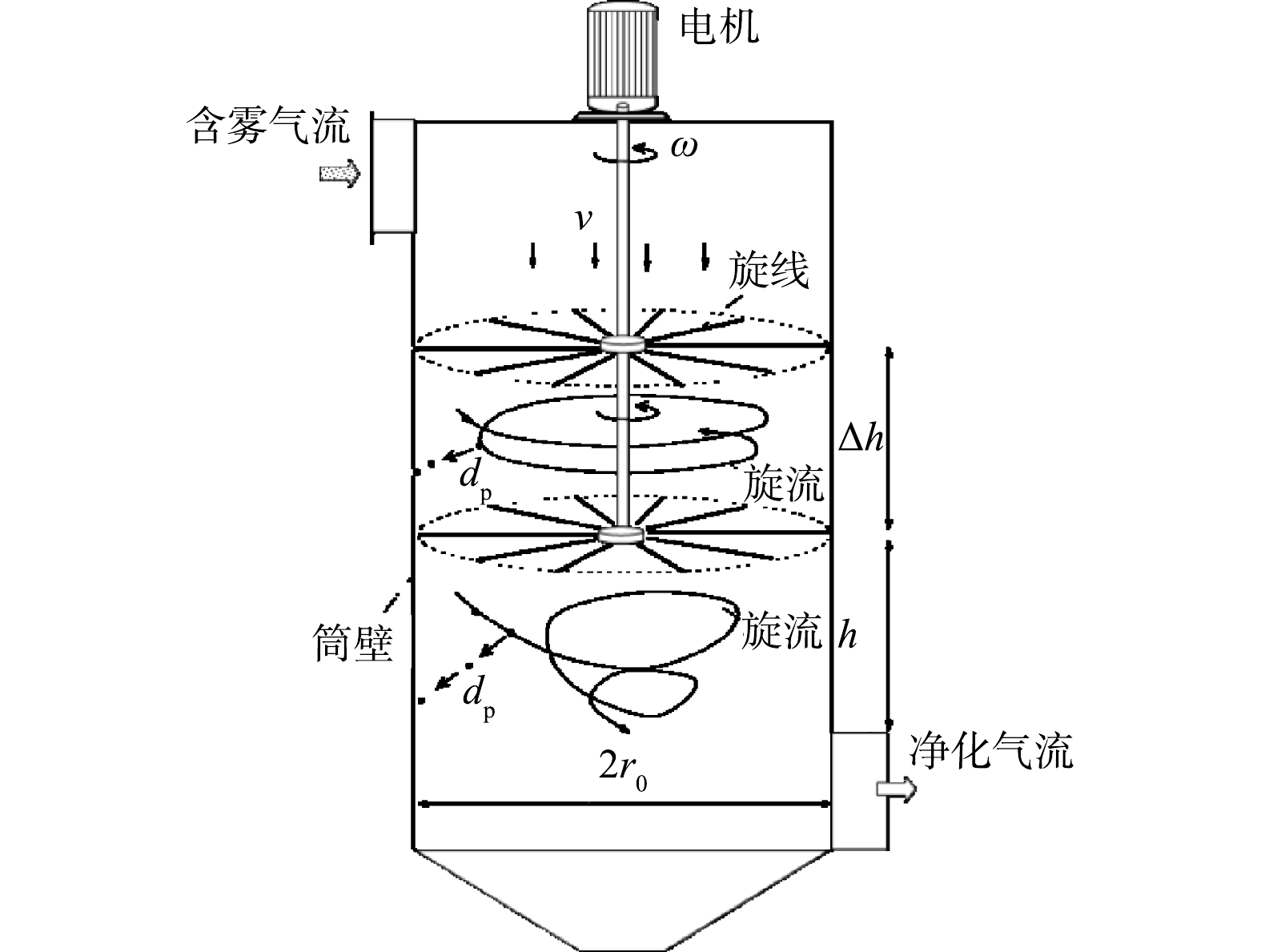
在旋线除雾器中布置有数以百计的纤维线(见图1)。纤维线的一端固定在电机的连接轴上,纤维线的另一端自由。电机启动前,纤维线在自重作用下自然下垂。电机启动后,高速旋转的纤维线(简称旋线)在离心力作用下呈伞形张开,并覆盖整个除雾器筒体过流断面。
当含雾气流进入除雾器,在通过旋线层时,柱状纤维旋线与液滴间产生拦截、惯性碰撞和扩散作用[19]。由于纤维线具有吸湿性,液滴会附着旋线表面或浸入旋线中,然后在离心力作用下甩向筒壁。筒壁上的液体在重力作用下最后流入除雾器底部的液斗中。另外,由于高速旋转的纤维线搅拌作用,使旋线层下方的气体形成旋流,进而对未被捕集的液雾产生离心分离作用,使旋线除雾器的净化效果得到进一步提升。所以,旋线除雾器的工作原理是旋线层过滤和旋流离心分离的协同作用。
1.2 旋线层的除雾效率
当圆柱状纤维与垂直于来流方向颗粒物之间的相对速度相同时,基于孤立圆柱状捕集体对颗粒物的捕集机理来探索纤维层的捕集效率更容易[20]。但由于旋线与雾滴的相对速度是变化的,需先根据不同的捕集机理确定单根旋线的捕集量,然后由效率定义分别建立旋线层的拦截、惯性碰撞和扩散效率理论表达式。
1.2.1 拦截
分析纤维对颗粒物的拦截捕集作用首先要考虑绕捕集体流动的介质的流态。对于绕流问题,分为黏性流和势流。判断流态的依据是雷诺数(Re),具体见式(1)。
Re=ρvdfμ (1) 式中:ρ为空气密度,kg·m−3;v为空气流速,m·s−1;df为旋线直径,m;μ为气体动力黏性系数,常温常压下,μ=1.85×10−5 Pa·s。
当Re≤1时,柱状捕集体周围的流动可视为黏性流;而当Re>1时,可近似为势流[21]。在自由旋线除雾器中,旋线的切向速度可超过10 m·s−1,且旋线较粗(直径通常2~4 mm)。由此得出,气流绕旋线流动的雷诺数Re超过100,属势流。在势流情况下,单位长度孤立圆柱状捕集体对球形雾滴的拦截效率计算公式[22]见式(2)。
ηr=1+G−11+G (2) 式中:ηr为单位长度孤立圆柱状捕集体对球形雾滴的拦截效率;G为拦截参数,计算式为式(3)。
G=dp/df (3) 式中:dp表示雾滴直径,m;df为旋线直径,m。
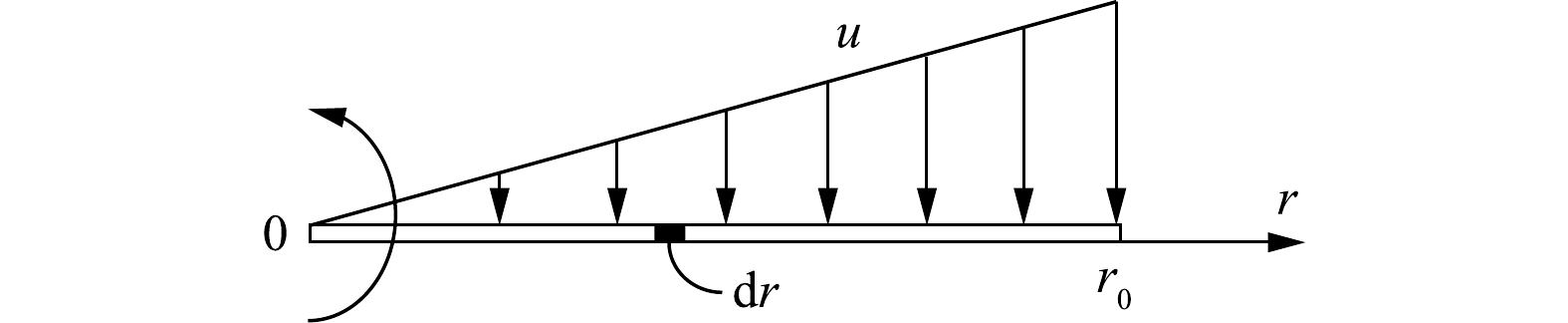
然而,沿旋线上的切向速度u是不均匀的,切向速度分布如图2所示。于是,旋线上任意点r与颗粒的相对运动速度见式(4)。
u=ωr (4) 式中:u为旋线与颗粒的相对速度,m·s−1;ω为旋线旋转角速度,rad·s−1;r为旋线半径,m。
设气体中的颗粒初始浓度为c0,在图2所示的旋线微元长度dr上拦截的雾滴质量计算式见式(5)。
dmR=c0ηrdfudr=c0ηrdfωrdr (5) 式中:dmR为微元dr上拦截的雾滴质量,kg;c0为气体颗粒浓度,kg·m−3。
对式(5)从0到旋线长度r0进行积分(见式(6)),得到单根旋线拦截作用捕集的雾滴质量。
mR=∫r00c0ηrdfωrdr=12c0ηrdfωr02 (6) 因流向孤立旋线的雾滴总质量的计算式见式(7)。于是,单根旋线拦截作用的捕集效率可通过式(8)进行计算。
M=Qc0=πr02vc0 (7) ηR=mRM=ωdf2πvηr (8) 式中:M为来流雾滴总质量,kg;Q为气流流量,m3·s−1;c0为气体颗粒浓度,kg·m−3;v为通过旋线除雾器筒体断面的平均轴向速度,m·s−1;ηR为单根旋线拦截作用的捕集效率;mR为单根旋线捕集雾滴质量,kg。
对于气流中有N个捕集体时(见图3),由计算式(9)[23],得到旋线层的拦截效率。
ηRN=1−(1−ηR)N (9) 1.2.2 惯性碰撞
当颗粒直径dp>1 µm,柱状捕集体的惯性碰撞效应是重要的。惯性碰撞效率是Stokes数St的函数,其表达式见式(10)。
St=ρpdp2u18μdf (10) 式中:ρp为雾滴密度,kg·m−3;dp为雾滴直径,m;u为捕集体与颗粒的相对速度,m·s−1;μ为气体动力黏性系数,取μ=1.85×10−5 Pa·s;df为旋线直径,m。
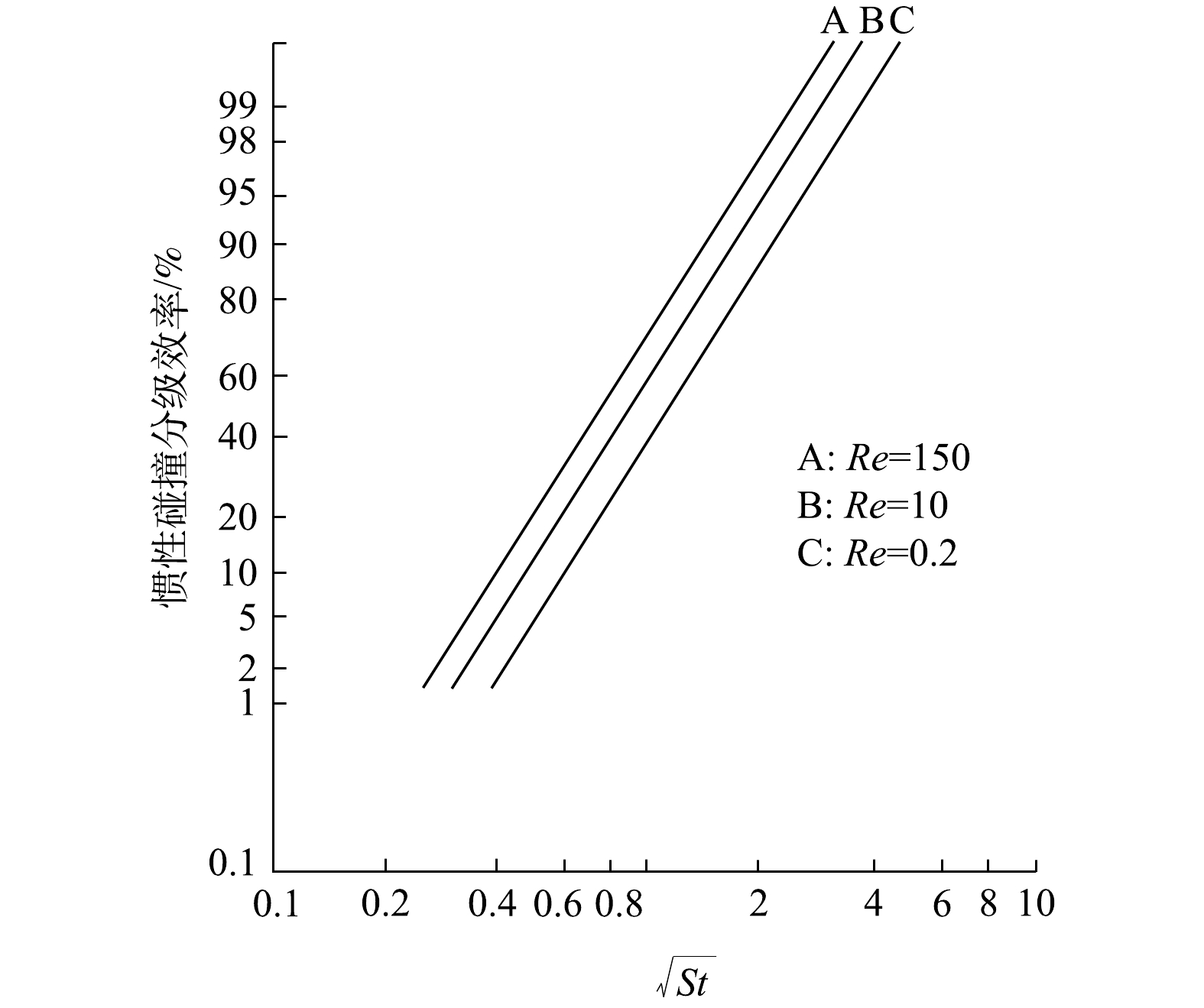
由于绕孤立柱状纤维流动的颗粒运动方程求解非常困难,至今没有分析解。虽然LANDAHL和HERMAN给出了惯性碰撞效率经验式[22],但在高雷诺数的势流情况下缺乏适用性论据。已有研究结果表明,在对数概率坐标纸上,单位长度孤立柱状捕集体的惯性碰撞效率随
√St 而能在对数概率坐标纸上具有直线分布特征的数学模型为对数正态分布。于是,惯性碰撞效率与
√St ηi=1lnσg√2π∫√St0exp[−(ln√St−ln√St50)22(lnσg)2]d(ln√St) (11) 式中:ηi为单位长度孤立圆柱状捕集体的惯性碰撞效率;σg为几何标准偏差;
(√St)50 对于旋线,符合Re≥150,满足曲线A,于是由图4可确定
(√St)50=0.7 σg=√St(ηi=84.1%)(√St)50=1.350.7≈1.9 (12) ηi=1ln1.9√2π∫√St0exp[−(ln√St−ln0.7)22(ln1.9)2]d(ln√St) (13) 来流颗粒与旋线的相对运动速度是变化的,故单根旋线上惯性碰撞捕集的液滴质量可由积分(见式(14))来计算。单根旋线的惯性碰撞捕集效率计算见式(15),而气流中有N根捕集体的惯性碰撞效率计算式见式(16)。
mI=∫r00c0ηidfωrdr (14) ηI=mIM=ωdfπr02v∫r00ηirdr (15) ηIN=1−(1−ηI)N (16) 式中:mI为单根旋线惯性碰撞作用捕集的液滴质量,kg;ηI为单根旋线的惯性碰撞捕集效率;ηIN为旋线层惯性碰撞捕集效率;N为旋线根数。
1.2.3 扩散效应
扩散效应适合于颗粒直径dp<1 µm的情况。但在水雾中,dp<1 µm液滴所占质量百分比极小,对总捕集效率的贡献很小,可忽略。
对于多机理同时存在的复合捕集效率,普遍采用RICHARD和SEINFELD 给出的算式[25] (见式(17))。于是,N根旋线的旋线层的拦截和惯性碰撞复合除雾效率计算式见式(18)。
η=1−(1−η1)(1−η2)⋯(1−ηn) (17) ηN=1−(1−ηRN)(1−ηIN) (18) 上述研究表明,降低气流速度、增加转速,均有助于增强拦截和惯性碰撞的捕集作用,但增加旋线根数的提效作用更突出。
1.3 旋流离心分离
旋线除雾器可采用单层或多层布置。由于每层旋线布置的根数是受限的,当旋线除雾器无法满足水雾排放要求时,可通过增加旋线层数提效。当采用多层布置时,在两旋线层之间形成较规则的旋涡流,对雾滴产生离心分离作用。
图1中,旋线层间的距离Δh应不小于旋线长度
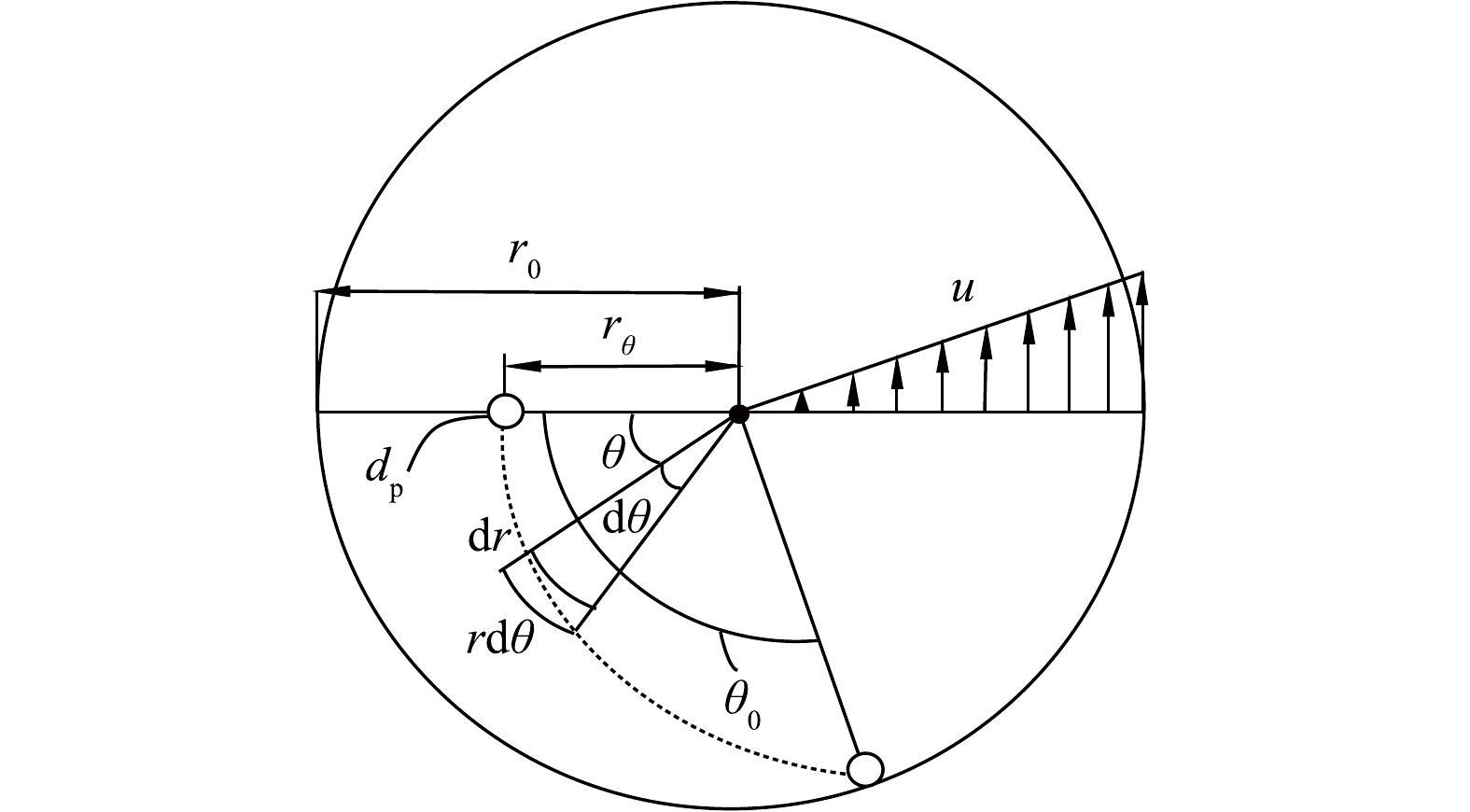
r0 t0=Δh/v (19) θ0=ωt0=ωΔh/v (20) 在图5所示的旋流场中,假定位于半径rθ直径为dp的雾滴随气流旋转θ角度后,沉降到r=r0的边壁上被捕集。
显然,对于位于rθ和r0之间直径为dp的所有雾滴将被捕集。因此,其旋流分离效率计算式见式(21)。
ηω=(r0−rθ)/r0=1−rθr0 (21) 由式(21)可知,下面应确定rθ的计算方法。在图5所示的雾滴轨迹线的任意点(r, θ)上,雾滴在dt时间内径向和切向运动距离计算式见式(22)。
dr=wdt,rdθ=udt (22) 式中:雾滴的离心沉降速度w计算式见式(23)。
w=τu2r (23) 式中:τ为弛豫时间,计算式见式(24)。
τ=ρpdp2Cc18μ (24) 式中:Cc 即Cunningham 滑移修正系数,对于dp>1 µm的粒子,Cc≈1。
由式(22)可换算得到式(25)。将式(23)代入式(25),得到式(26)。将式(4)代入式(26),积分得到式(27)。由式(27)得到式(28)。将式(28)代入式(21)得旋流离心分离效率计算式(29)。将式(20)代入式 (29),旋流离心分离效率还可由式(30)计算得到。
drdθ=rwu (25) dr=τudθ (26) ∫r0rθdrr=∫θ00τωdθ (27) rθ=r0e−ωτθ0 (28) ηω=1−rθr0=1−e−ωτθ0 (29) ηω=1−rθr0=1−exp(−τΔhω2v) (30) 可见旋流离心分离除雾效率服从指数变化规律,且是雾径和转速平方的函数。在图1所示的第二层旋线下面仍有呈锥状收缩的旋流流动,但因接近气流出口,旋流衰减较快,故忽略其离心分离作用。
于是,双层旋线捕集和旋流离心分离协同除雾效率计算式为式(31)。
ηC=1−(1−ηN)2(1−ηω)=1−[(1−ηRN)(1−ηIN)]2(1−ηω) (31) 2. 旋线除雾理论的验证
2.1 实验系统
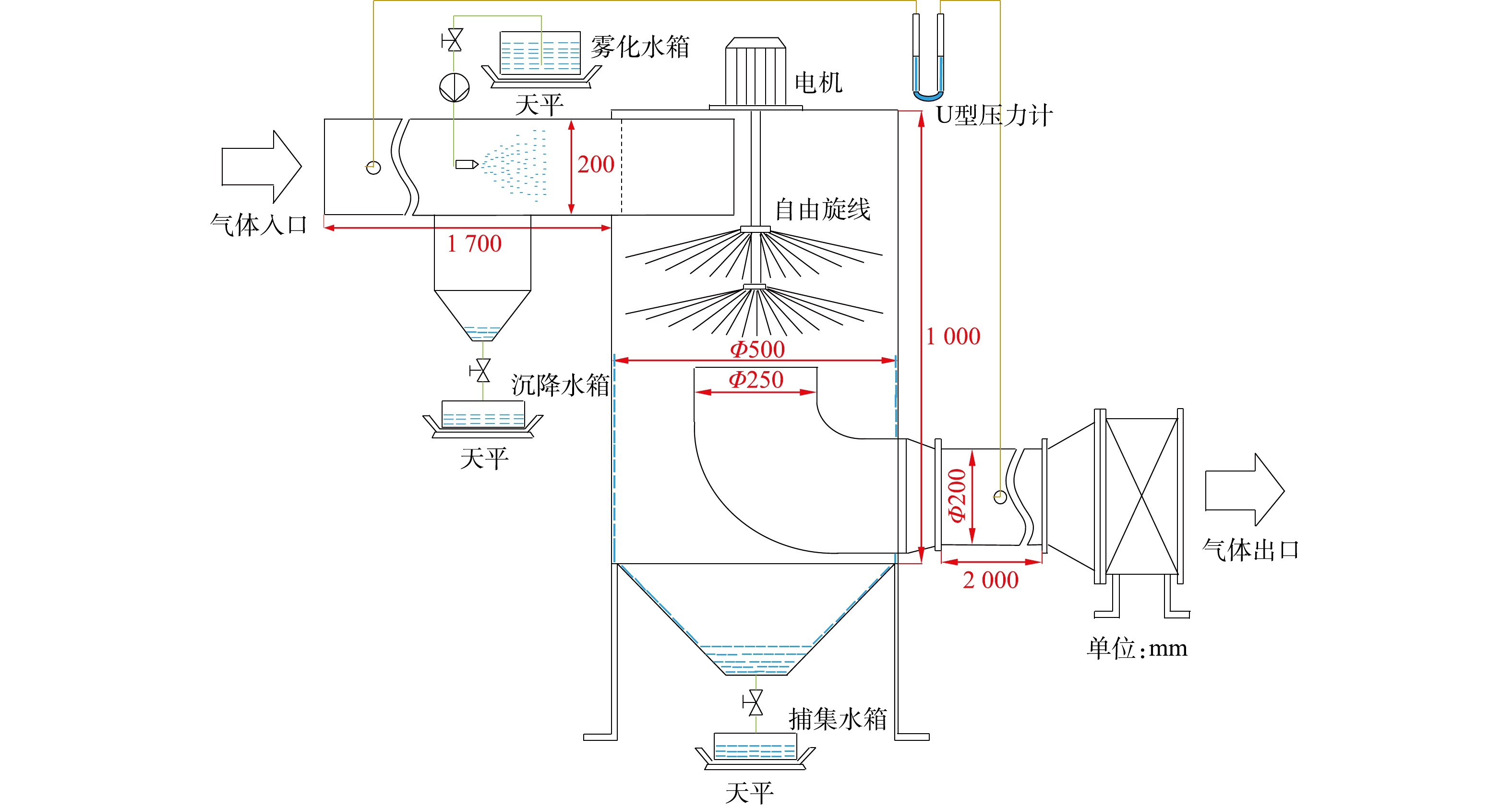
双层旋线除雾实验系统如图6所示。由除雾器本体、水泵、电机、旋线、风机、水箱构成。入口管均布4个雾化喷嘴,壳体采用8 mm厚有机玻璃,旋线长250 mm,材质采用3 mm聚酯纤维线。风机最大风量5 000 m3·h−1,全压300 Pa。
2.2 实验方法
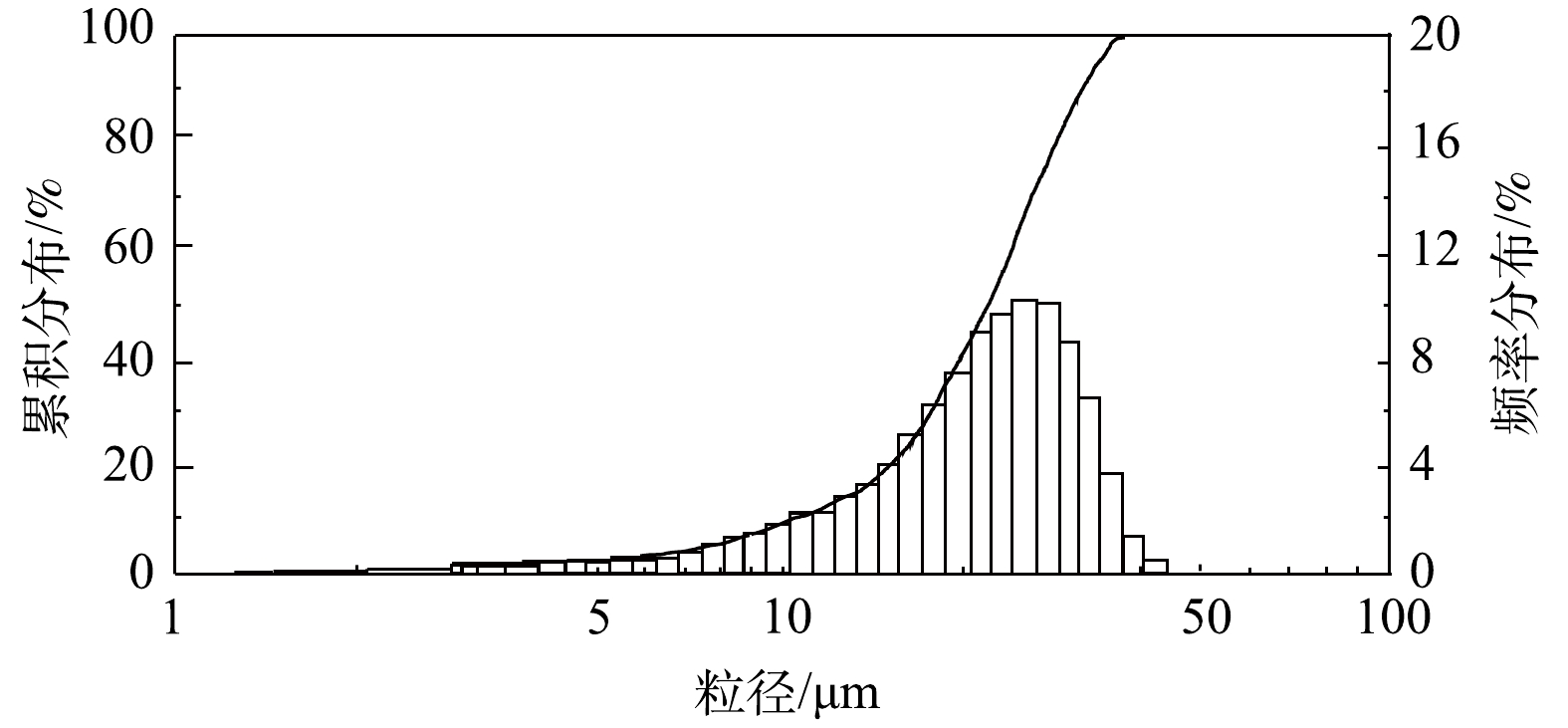
风量和旋线转速均采用变频器控制。通过调节水压改变水雾直径,采用Winner 318激光粒度分析仪测定实验水雾的粒径分布如图7所示。水雾中位径为20.1 μm,实验雾滴大小接近工业脱硫塔烟气夹带液滴的粒径范围[26]。
除雾效率的测定采用水平衡法[27]。在图6中,雾化水箱的失水量为喷嘴总喷水量m1,喷头喷出的雾化水雾随气流运动,喷到进气管壁上的雾滴汇入沉降水箱中,水量为m2。实际进入旋线除雾器筒体的总水雾量m0=m1−m2,被旋线旋线捕集的雾滴流入捕集水箱中,水量为mc,则除雾效率见式(32)。
ηT=mc/m0 (32) 2.3 实验条件
实验在常温常压下进行,双层旋线除雾器每层旋线根数分别取100根和200根。考虑到现有静电除雾器的处理风速通常不超过2 m·s−1[28],为体现旋线除雾器的优势,实验风速取2.5 m·s−1。喷嘴的喷液量为1 355 kg·h−1,水雾浓度为4 100 mg·m−3。
2.4 检验结果与讨论
2.4.1 效率理论的检验
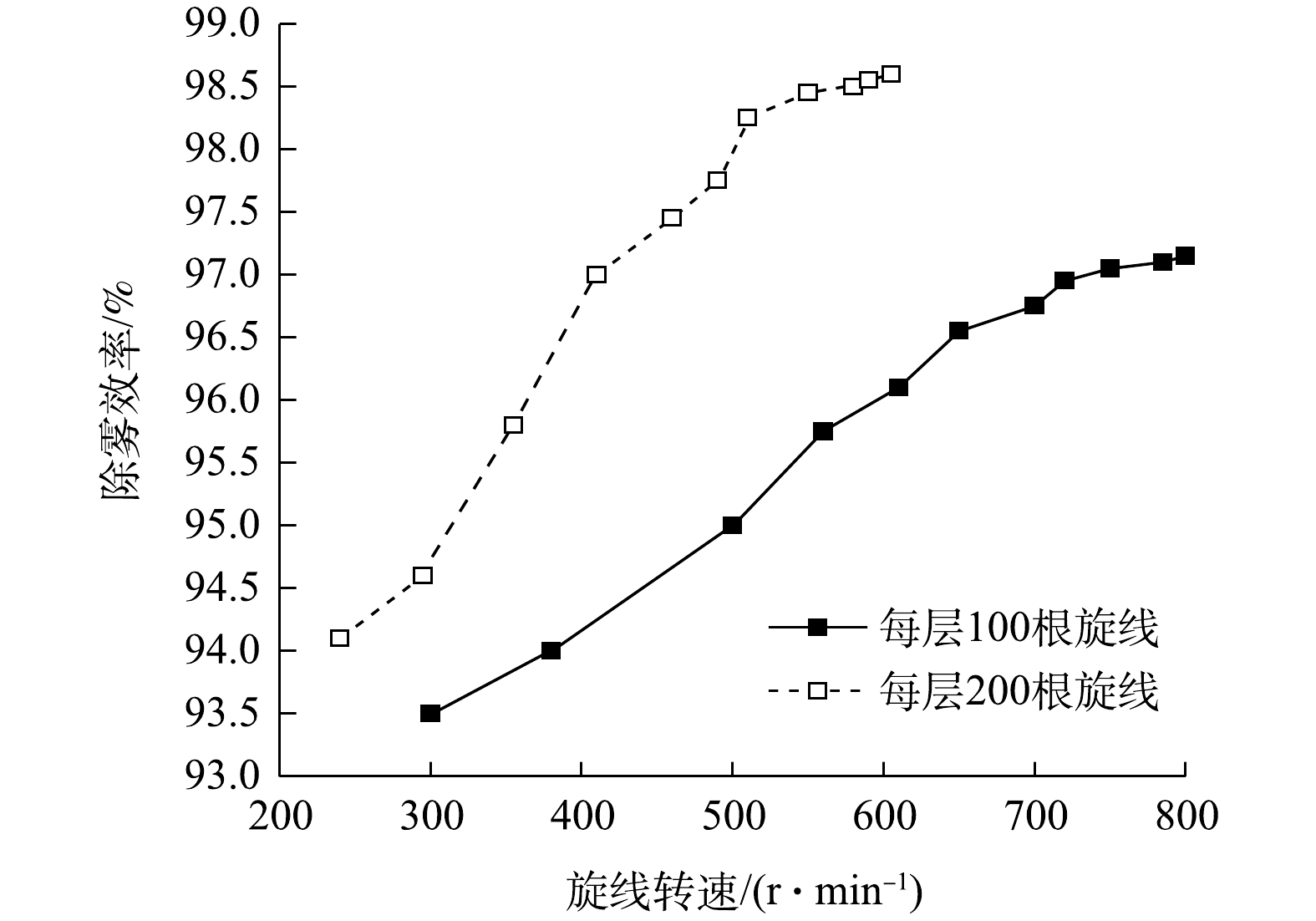
当每层旋线分别为100根和200根时,测得双层旋线除雾器的除雾效率与旋线转速的关系如图8所示。
结果表明,增加旋线根数的提效作用非常显著。采用直径3 mm旋线捕集中位径20.1 μm的水雾,当旋线转速500 r·min−1时,每层旋线为100根时除雾总效率约95%,当旋线增至每层200根时,除雾总效率为98.1%。
由于实验所测得的除雾效率是总除雾效率,所建立除雾效率理论式(31)是分级效率,二者无法比较。为将实验所得总效率与分级效率相联系以便于评价除雾器的性能,ZHAO等[29]通过大量实验数据和试错研究发现,颗粒群的总捕集效率和颗粒群中位径近似存在的关系如式(33)所示。
ηT=1−exp(−k0dp50) (33) 式中:ηT为总效率实验值;k0为待定系数;dp50为颗粒群中位径。
根据已知总效率实验值ηT和颗粒群中位径dp50,由式(33)可确定系数k0。于是,基于分级效率服从指数规律,ZHAO等[29]得出预估分级效率经验式(34)。
ηe=1−exp(−k0dp) (34) 式中:ηe为预估分级效率。
作为验证性研究,仅讨论旋线转速500 r·min−1情况下分级效率理论值与分级效率经验预估值的吻合度。
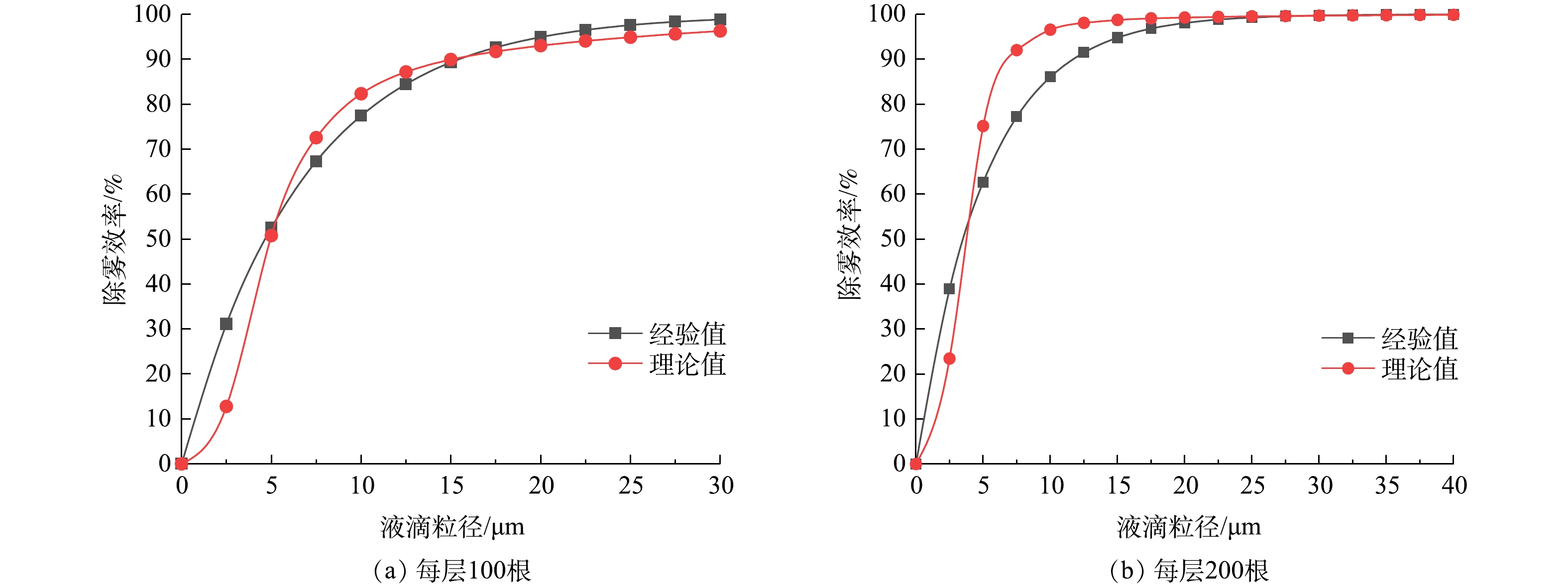
由总效率实验结果图8和式(33)得出的k0值(见表1)。由式(34)分别得出每层100根和200根时的分级效率经验值ηe,然后由式(31)得出双层旋线除雾器分级效率理论值ηC,将计算结果绘于图9中。
表 1 k0值计算表Table 1. Calculation value of k0转速n/(r·min−1) 角速度ω/(rad·s−1) 每层旋线根数 总效率实验值/% k0 500 16.7π 100 95.0 0.149 200 98.1 0.197 实验结果表明,当雾径小于5 μm,旋线除雾器分级效率理论值低于经验值;当雾径为5~20 μm时,理论值高于经验值,随后二者相互逼近。上述现象的原因是,当雾径小于5 μm,惯性碰撞效应较弱,而当雾径大于5 μm,惯性碰撞作用明显增强。总体看,旋线除雾器分级效率理论值与经验值相当吻合,在雾径为0~40 μm时,平均误差约1.4%,说明双层旋线的拦截、惯性碰撞与旋流离心分离复合除雾效率理论是比较准确的。
2.4.2 不同机理的提效作用
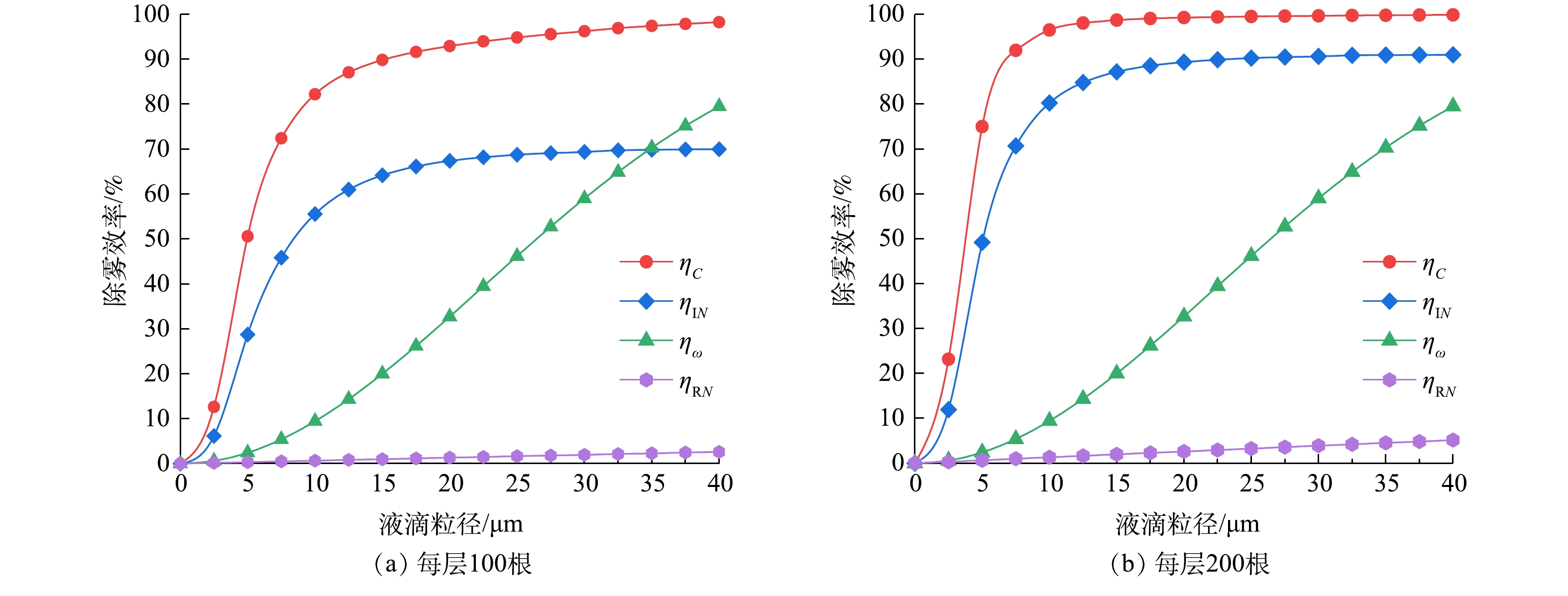
为明确各捕集机理在旋线除雾中的作用,取旋线转速500 r·min−1,将单层拦截ηRN、惯性碰撞ηIN、旋流离心分离ηω和双层复合除雾效率ηc的计算结果绘于图10中。由图10可看出,惯性碰撞效应起主导作用,旋流分离次之,拦截效率对旋线除雾器效率的贡献很小。如对20 μm雾滴,在每层旋线
N=200 3. 结论
1)旋线除雾器的除雾机理主要是拦截、惯性碰撞和旋线的高速旋转产生的旋流离心分离。理论研究表明,拦截和惯性碰撞随旋线转速和旋线根数的增加而提高,但增加旋线根数的提效作用更有效;旋流离心分离效率是雾径和转速的平方的函数,且服从指数规律。
2)双层旋线除雾器的理论分级效率的验证结果表明,在旋线转速500 r·min−1、旋线直径3 mm、每层旋线分别为100根和200根的情况下,在0~40 μm雾径范围内,旋线除雾器分级效率理论值与经验值基本吻合,平均误差约1.4%,说明双层旋线器的复合除雾效率理论是比较准确的。
3)对比各机理在旋线除雾器中的提效作用可看出,旋线的惯性碰撞效应起主导作用,特别是对小粒径的雾滴有较高的捕集效率;旋流离心分离作用次之,对于小粒径雾滴分离效率不高,但随着雾滴粒径的增加效率提升较快;旋线的拦截除雾效率较低,几乎可以忽略不计。
-
表 1 不同截面形状纤维的异形度和形状系数
Table 1. Parameters of different cross-sectional shapes fibers of the alien degree and shape factor
截面形状 径向异形度 截面异形度 形状系数 圆形 0.000 0 0.000 0 12.560 0 正三角形 0.500 0 0.750 0 20.632 6 正方形 0.297 7 0.506 8 15.999 9 正五边形 0.191 0 0.345 5 14.631 0 正六边形 0.134 0 0.250 0 13.264 0 正八边形 0.076 1 0.146 4 12.271 8 -
[1] JIA J, CHENG S Y, YAO S, et al. Emission characteristics and chemical components of size-segregated particulate matter in iron and steel industry[J]. Atmospheric Environment, 2018, 182: 115-127. doi: 10.1016/j.atmosenv.2018.03.051 [2] SUN W Q, ZHOU Y, LU J X, et al. Assessment of multi-air emissions: Case of particulate matter(dust), SO2, NOx and CO2 from iron and steel industry of China[J]. Journal of Cleaner Production, 2019, 232: 350-358. doi: 10.1016/j.jclepro.2019.05.400 [3] 汪旭颖, 燕丽, 雷宇, 等. 我国钢铁工业一次颗粒物排放量估算[J]. 环境科学学报, 2016, 36(8): 3033-3039. [4] 袁学玲, 陈晓春, 杨正羽, 等. 湿度对袋式除尘性能的强化研究[J]. 高校化学工程学报, 2019, 33(4): 965-971. doi: 10.3969/j.issn.1003-9015.2019.04.024 [5] 万凯迪, 王智化, 胡利华, 等. 袋式除尘器脉冲喷吹清灰过程的数值模拟[J]. 中国电机工程学报, 2014, 34(23): 3970-3976. [6] DAVIES C N. Air Filtration[J]. London:Academic Press Inc, 1973: 123-128. [7] 宗亚宁. 纺织材料学[J]. 上海: 东华大学出版社, 2013: 115-117. [8] 孙熙, 邓云峰, 李辉, 等. 异形纤维过滤器流场及阻力数值分析模型[J]. 沈阳建筑工程学院学报, 1998, 14(2): 131-135. [9] 王浩明, 赵海波, 郑楚光. 格子波尔兹曼两相流动模型模拟椭圆纤维捕集颗粒物过程[J]. 中国电机工程学报, 2013, 33(8): 50-57. [10] 顾丛汇, 吕士武, 李瑞, 等. 纤维对PM2.5过滤性能的影响[J]. 化工学报, 2014, 65(6): 2137-2147. doi: 10.3969/j.issn.0438-1157.2014.06.026 [11] 王坤, 赵海波. 异形纤维捕集颗粒过程的格子Boltzmann法数值模拟[J]. 中国粉体技术, 2015, 21(6): 1-7. [12] 杨会, 朱辉, 陈永平, 等. 方形截面纤维表面气溶胶粒子多机理过滤性能数值分析[J]. 过程工程学报, 2020, 20(4): 400-409. doi: 10.12034/j.issn.1009-606X.219270 [13] RAYNOR P C. Flow field and drag for elliptical filter fibers[J]. Aerosol Science & Technology, 2002, 36(12): 1118-1127. [14] HOSSEINI S A, TAFRESHI H V. On the importance of fibers’ cross-sectional shape for air filters operating in the slip flow regime[J]. Power Technology, 2011, 212: 425-431. doi: 10.1016/j.powtec.2011.06.025 [15] FOTOVATI S, TAFRESHI H V, POURDEYHIMI B. Analytical expressions for predicting performance of aerosol filtration media made up of trilobal fibers[J]. Journal of Hazardous Materials, 2011, 186: 1503-1512. doi: 10.1016/j.jhazmat.2010.12.027 [16] SALEH A M, TAFRESHI H V. On the filtration performance of dust-loaded frilobal fibers[J]. Separation and Purification Technology, 2015, 149: 295-307. doi: 10.1016/j.seppur.2015.06.005 [17] HUANG H K, WANG K, ZHAO H B. Numerical study of pressure drop and diffusional collection efficiency of several typical noncircular fibers in filtration[J]. Powder Technology, 2016, 292: 232-241. doi: 10.1016/j.powtec.2016.02.012 [18] HUANG H K, ZHENG C H, ZHAO H B. Numerical investigation on non-steady-state filtration of elliptical fibers for submicron particles in the ''Greenfield gap'' range[J]. Journal of Aerosol Science, 2017, 114: 263-275. doi: 10.1016/j.jaerosci.2017.09.018 [19] BONATO P, DANTONI M, FEDRIZZI R. Modelling and simulation-based analysis of a facade-integrated decentralized ventilation unit[J]. Journal of Building Engineering, 2020, 29: 1-12. [20] BAI Y, SI H, WANG X. Steady-state simulation of internal heat-transfer characteristics in a double tube reactor[J]. Chemical Engineering and Processing, 2019, 144: 1-9. [21] DU S, WU M, CHEN L F, et al. A fuzzy control strategy of burn-through point based on the feature extraction of time-series trend for iron ore sintering process[J]. IEEE Transactions on Industrial Informatics, 2020, 16(4): 2357-2368. doi: 10.1109/TII.2019.2935030 [22] AMIRI Z, MOVAHEDIRAD S. Bubble-induced particle mixing in a 2-D gas-solid fluidized bed with different bed aspect ratios: A CFD-DPM study[J]. Powder Technology, 2017, 320: 637-645. doi: 10.1016/j.powtec.2017.07.097 [23] XIAO Z F, LE J B, WU N X. Three-dimensional numerical simulation on ceramic slurry spray drying by DPM[J]. Journal of Synthetic Crystals, 2015, 44(6): 1690-1696. [24] PETERS B. Measurements and application of a discrete particle model(DPM) to simulate combustion of a packed bed of individual fuel particles[J]. Combustion and Flame, 2002, 131:132-146. [25] SEUNGKOO K, LEE H, SEONG C K. Modeling of fibrous filter media for ultrafine particle filtration[J]. Separation and Purification Technology, 2019, 209: 461-469. doi: 10.1016/j.seppur.2018.07.068 [26] LI W, SHEN S N, LI H. Study and optimization of the filtration performance of multi-fiber filter[J]. Advanced Powder Technology, 2016, 27: 638-645. doi: 10.1016/j.apt.2016.02.018 [27] KUWABARA S. The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small Reynolds numbers[J]. Journal of the Physical Society of Japan, 1959, 14: 527-532. doi: 10.1143/JPSJ.14.527 [28] HAPPEL J. Viscous flow relative to arrays of cylinders[J]. AIChE Journal, 1959, 5(2): 174-177. doi: 10.1002/aic.690050211 [29] LIU Z G, WANG P K. Pressure drop and interception efficiency of multifiber filters[J]. Aerosol Science and Technology, 1997, 26(4): 313-325. doi: 10.1080/02786829708965433 [30] SEUNGKOO K, HANDOL L, CHAN K S, et al. Modeling of fibrous filter media for ultrafine particle filtration[J]. Separation and Purification Technology, 2018, 209: 461-469. [31] WANG H, ZHAO H, WANG K, et al. Simulation of filtration process for multi-fiber filter using the Lattice-Boltzmann two-phase flow model[J]. Journal of Aerosol Science, 2013, 66: 164-178. doi: 10.1016/j.jaerosci.2013.08.016 -






 下载:
下载: